考虑强度和刚度退化及捏拢效应的钢筋混凝土桥墩滞回模型及其参数识别
2015-05-09董慧慧
韩 强, 董慧慧, 郭 婕
(北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124)
考虑强度和刚度退化及捏拢效应的钢筋混凝土桥墩滞回模型及其参数识别
韩 强, 董慧慧, 郭 婕
(北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124)
为了有效地模拟强震作用下桥梁结构的非线性地震反应,需要确定钢筋混凝土(RC)桥墩非线性力-位移滞回关系。基于Bouc-Wen模型,提出了一种考虑RC桥墩强度和刚度退化以及捏拢效应的改进非线性滞回模型,确定了影响该滞回模型的控制参数,并在Matlab/Simulink里实现了对RC桥墩各种破坏模式非线性滞回性能预测。同时,通过对1/3比尺的RC桥墩分别在压弯、扭转和弯剪作用下的往复荷载试验研究,试验得到的力-位移关系滞回曲线与所提的改进滞回模型预测结果吻合较好,验证了改进模型的正确性和有效性。并采用汶川地震波对绵州市回澜立交桥匝道桥的RC桥墩的滞后性能进行了数值模拟,分析结果和桥墩的震害一致,证实了采用本文提出的改进滞回模型可以较准确地预测RC桥墩在强震作用下的非线性滞后性能。在此基础上,运用无迹卡尔曼(UKF)方法对Bouc-Wen模型进行参数估计,模拟结果和误差分析表明,该方法能够精确的估计出改进的Bouc-Wen模型的参数。
钢筋混凝土桥墩; 滞回模型; 刚度和强度退化; 捏拢效应; 参数识别
引 言
许多工程结构在动荷载作用下会进入非弹性状态而表现出滞回特性[1-3]。滞回特性也称为弹塑性,滞回一般来自材料的非线性特性、接触面的摩擦特性和结合面之间的接触变形等,在荷载作用下这些结构的恢复力与位移之间存在滞回关系,当荷载具有周期性时,在加载和卸载的过程中,曲线不是沿同一路径变化,而是形成了滞回环,即称之为滞回曲线。
结构的实际滞回曲线十分复杂,难以应用于分析结构的非线性特性,因而需要建立既便于数学描述又能反映结构滞回特性的滞回模型来预测工程结构非线性动力响应。为描述结构这一复杂的非线性滞回特性,研究人员提出了一些滞回模型,根据滞回模型曲线的光滑程度,可将这些滞回模型分为折线型模型和光滑型模型两类[4]。折线型模型采用线段直观的描述试验所得恢复力曲线的加卸载规则,如双线性模型、Clough模型[5]、Takeda模型[6]、Saiidi等人提出的Q模型[7]等。由于折线模型是一种简单的滞回模型,刚度计算较简单,所以在实际工程中得到广泛应用。但是由于刚度变化不连续,存在拐点或突变点,在非线性分析时往往会产生累积误差,与实际情况不太符合,并且若在多折线模型中考虑强度和刚度退化以及捏拢滑移等诸多特征,则加卸载路径比较复杂,不方便程序实现,且缺乏通用性。另一种是光滑型模型,首先由Bouc[8]在1967年提出,采用微分形式的数学模型来模拟滞回非线性系统,随后Wen[9,10]和Baber[11]等人发展了这个数学模型,使这个数学模型可以比较精确的表征各种非线性系统滞回特性。光滑型模型的刚度是连续变化的,与实际工程较为接近,不足之处在于刚度计算方法比较复杂,随着计算机运算功能的提高,光滑滞回模型的运算效率和精度大大提高,从而使光滑滞回模型的应用更加广泛。
桥墩作为支撑桥梁上部结构并将上部荷载传递至基础的重要受力构件,是地震中桥梁结构中易损伤破坏的构件,桥墩的承载力直接影响着桥梁整体结构抵抗地震的能力。因而,对RC桥墩的非线性滞回性能的精细化表征是桥梁结构抗震分析的基础。由于钢筋混凝土材料的非线性、混凝土裂缝开合、钢筋-混凝土之间黏结滑移、疲劳损伤累积等对结构强度和刚度的影响,RC桥墩的恢复力曲线呈现复杂的滞回特征。本文基于Bouc-Wen模型,根据RC桥墩所具有的复杂滞回特性,提出了一种考虑刚度退化、强度退化和捏拢效应的改进滞回模型,根据各个参数对滞回曲线形状的影响,通过辨别确定控制参数可以模拟不同破坏模式下RC桥墩的滞回特性,并通过与1/3比例尺RC模型桥墩在压弯、扭转和弯剪往复荷载作用下试验结果进行对比,对该模型的正确性和有效性进行验证。进一步运用该改进模型,数值模拟了绵竹市回澜立架桥匝道桥的RC桥墩在2008年汶川地震作用下的性能。同时运用无迹卡尔曼方法对Bouc-Wen模型进行参数估计。
1 改进的Bouc-Wen模型
1.1 Bouc-Wen模型
Wen[8]等修改了Bouc[9,10]提出的由微分方程控制的光滑滞回模型,并使其系统化,单自由度(SDOF)滞回系统可以用图1表示。

图1 单自由度滞回系统Fig.1 SDOF hysteresis model
该模型的控制方程为
(1)

为了研究滞回模型,提高模型参数辨别的精度,预先对数据进行规范化得到无量纲的滞回曲线如图2所示,延性为位移与屈服位移的比值。恢复力F表示为

(2)
其中滞回位移的导数表示为
(3)
式中A为模型参数,后来A被证明是赘余的[12];β为控制滞回环形状的参数;γ为控制滞回环大小的参数;n为控制滞回环光滑度的参数。一般情况下,A,β,n取正数,γ取正负均可[13]。

图2 Bouc-Wen滞回曲线Fig.2 Bouc-Wen hysteresis curve
1.2 考虑刚度和强度退化的滞回模型

(4)
式中η(ε),ν(ε)分别为刚度退化函数和强度退化函数。

图3 滞回能量耗散示意图Fig.3 Hysteresis energy dissipation
吸收的滞回能量等于滞回系统的能量耗散,即可用如图3所示的滞回环所围成的面积表示,能量耗散是表示累积损伤的有效方法,因为其能反应加载历史并且类似于损伤演化的过程,累积滞回耗能是恢复力滞回变形的重要特征,其能综合反映系统变形的的能力,既便用于Bouc-Wen退化模型对系统进行定量研究。单位质量吸收的滞回能量E(t)表示
(5)
式中E(t)通过对时间的积分得到,η(ε),ν(ε)随着E(t)的变化而变化,z随着ν(ε),η(ε)的增加而减小。卸载和反向再加载的刚度退化与强度退化的效应都与构件的耗能累积损伤有关,所以把它们定义成滞回吸收能量的线性函数,分别表示
(6)
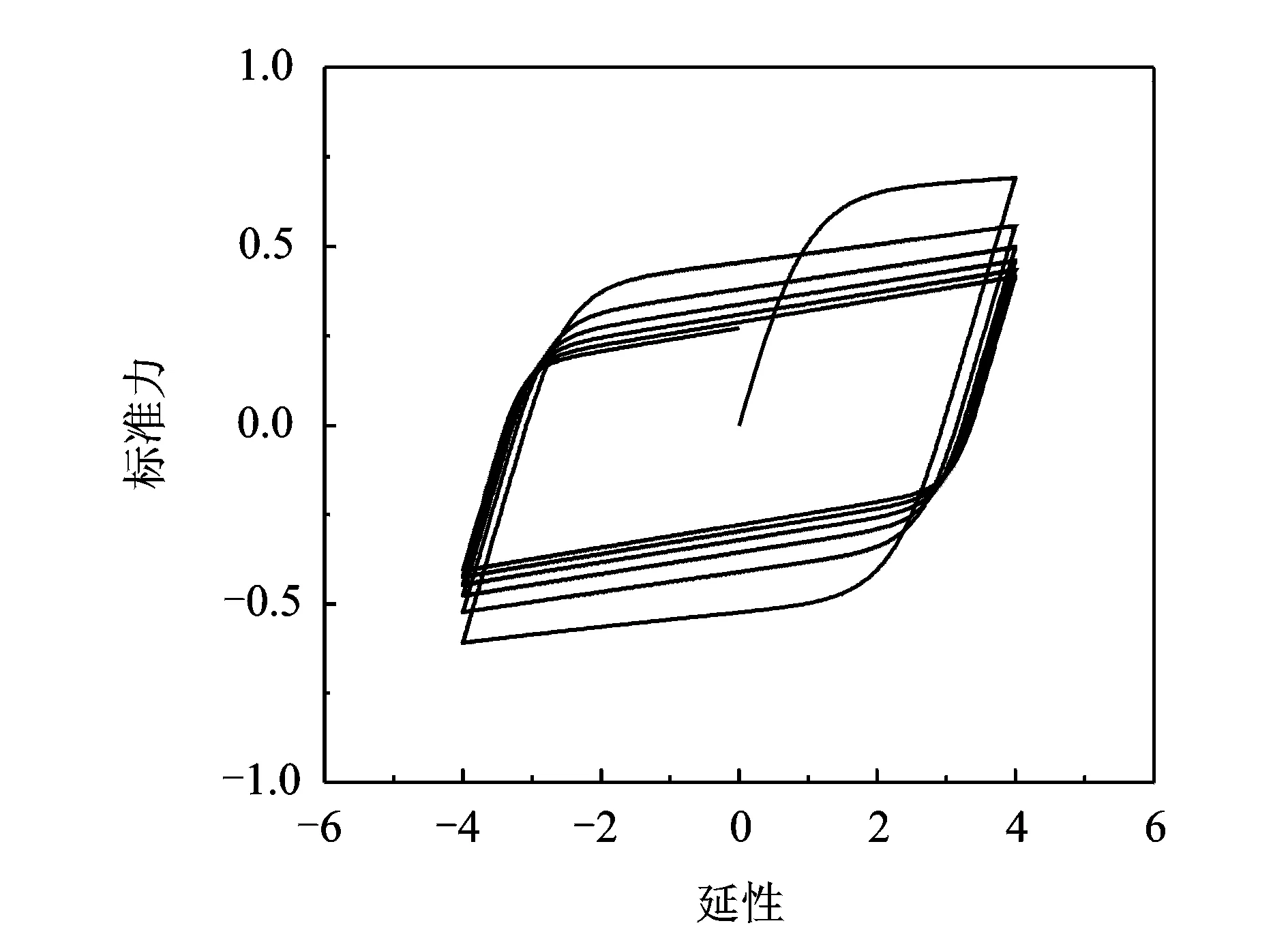
图4 仅有强度退化的滞回曲线Fig.4 Hysteresis loop of the differential model with only strength degradation

图5 仅有刚度退化的滞回曲线Fig.5 Hysteresis loop of the differential model with stiffness degradation
(7)
该系统进行正弦函数加载规则,当仅有强度退化时(刚度退化系数δν=0),得到滞回曲线如图4所示,每一滞回环加载和卸载时的斜率是相同的,而每一滞回环所达到的最大强度递减。当仅有刚度强度退化时(强度退化系数δη=0),得到的滞回曲线如图5所示,在相同变形位移的情况下,从图中明显看出随着滞回环的增加,滞回环加卸载时的刚度逐渐减小。当既有强度退化又有刚度退化时,滞回曲线如图6所示,刚度和强度都有明显的退化现象。

图6 刚度、强度退化的滞回曲线Fig.6 Hysteresis loop of the differential model with-strength degradation and stiffness degradation
1.3 改进的考虑退化和捏拢效应的滞回模型
RC桥墩在遭受地震时,根据结构的特性,刚度退化、强度退化和捏拢效应是并存的,所以在研究滞回模型的过程中需要综合考虑包括退化和捏拢效应。RC桥墩滞回系统出现捏拢归因于很多方面,主要是由混凝土裂缝的开合和钢筋-混凝土间粘结滑移等原因造成的。
Baber和Noori[16]通过在Bouc-Wen模型上增加滑移-锁定单元来考虑捏拢滑移效应。如图7所示,捏拢滞回系统的位移分解为两部分,一部分是光滑退化模型的变形,另一部分是滑移-锁定单元的变形,微分形式为
(8)
(9)
滞回环的捏拢效应是通过增加了一个以时间为依据的滑移单元来实现的,根据图1和7,u2的速率形式可以表示为
(10)
从图8中可以看出滑移单元类似于硬化的非线性弹簧,在滑移的区域,刚度几乎为零,在锁定区域,刚度达到无限大。图8反映的关于z的函数f(z)的特性为:
1.f(z)为一个分段函数,不随着z和u2符号的改变而改变;
2.f(z)的值除了在z=0时的一小段区域内达到最大值,其余值几乎都为零。
根据f(z)的这些特性,在这里选用高斯密度数表示z与f(z)的关系,即表示为
(11)

(12)

图7 滑移-锁定单元对滞回形状的影响Fig.7 The influence of the shape of hysteresis with slip-lock element

图8 滑锁函数Fig.8 Slip-lock function

(13)
因此屈服位移fy表示为
(14)
这样,对式(11)进行了扩展修改,最后形成的模型可以表示为
(15)
其中函数h(z,ε)表示为
h(z,ε)=1-ζs(1-e-pε)·

式中ζs为总滑移的尺寸;q为捏拢初始量;p为捏拢斜率;ψ为捏拢的量级;δψ为捏拢率;λ为捏拢比率。
图9所描述的滞回曲线既包括了强度退化和刚度退化,又考虑了捏拢效应,该模型的滞回恢复力与相对变形量关系更加符合RC桥墩在地震作用下滞回性能,合理选择模型的参数可以模拟RC桥墩在不同复杂受力状态下的滞回系统,并可应用于实际RC桥梁工程非线性地震反应分析之中。
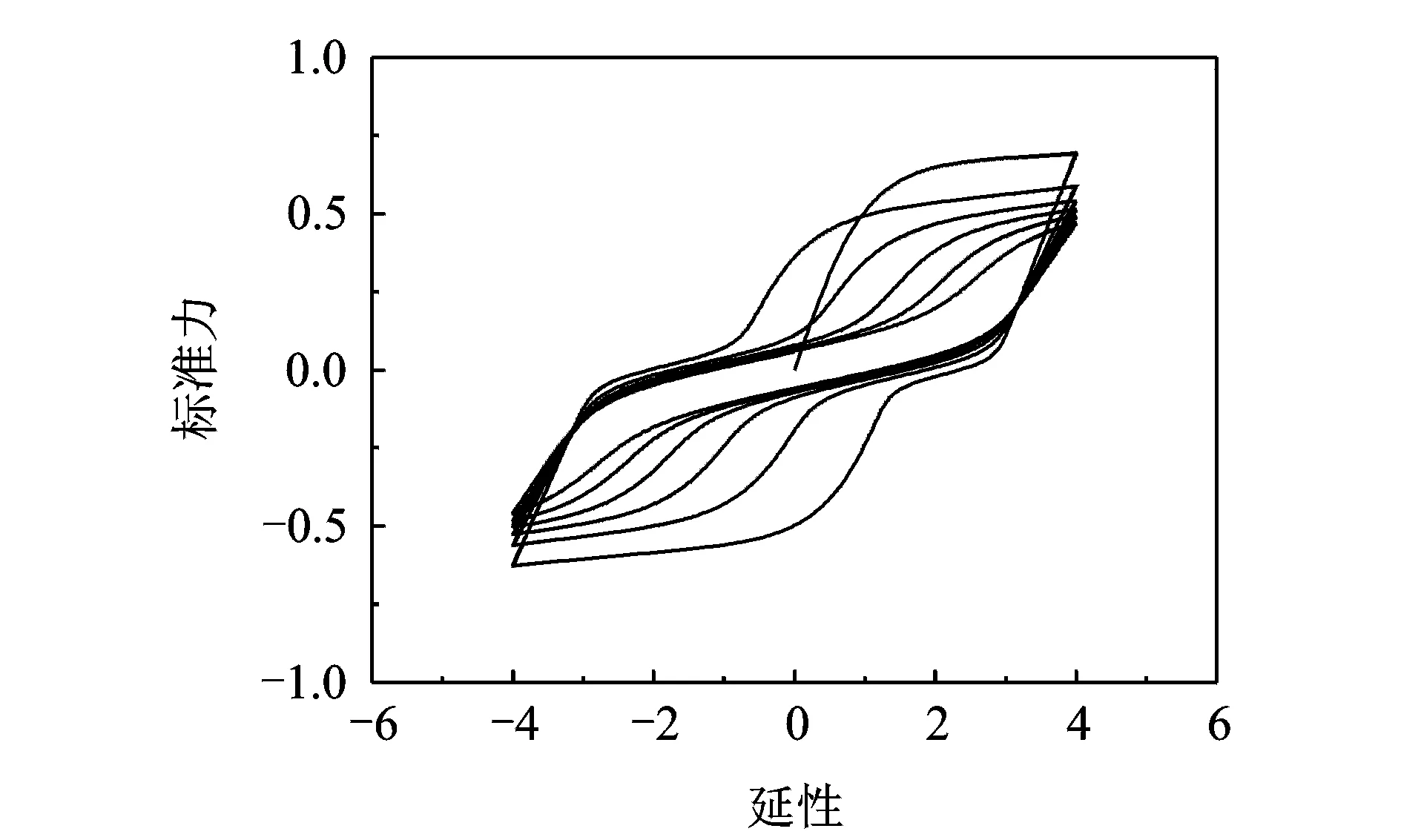
图9 刚度、强度退化现象和捏拢效应共同作用的滞回曲线Fig.9 Hysteresis loops with stiffness degrading, strength degrading and pinching
2 运用MATLAB软件数值模拟
由于Bouc-Wen模型微分方程的非线性和复杂性,若在Matlab软件中通过程序设计的方法对模型的所有微分方程进行数值求解会使得解析过程相当繁琐且工作量非常大。在本文中采用Matlab软件中的Simulink模块来完成该微分方程的求解。Simulink采用图框的方式来描述各种各样的数学表达式,清晰易懂,从而避免了繁琐复杂的数学描述,其就像一个黑匣子一样只需知道输入和输出之间的关系就能够建立模型进而求出解析解。
3 滞回曲线形状影响参数分析
在Bouc-Wen模型中,结构的恢复力与变形关系可以表述为一个具有不确定参数的非线性微分方程组,通过合理的选择参数,可以得到不同形状的滞回环,以模拟实际工程问题中结构或构件的非线性滞回特性。
Bouc-Wen模型中的14个待定参数中,除c,k,α是描述结构本身性质的参数外,其余的11个均为描述模型滞回特性的模型参数,这11个参数对滞回曲线的变化必定具有不同的影响力,本文分别分析了这11个参数对滞回曲线的形状的影响。
如图10所示,随着n取值的变大,滞回环逐渐由光滑变成线性,当n=∞时,滞回环为双线性,参数n主要控制滞回曲线的光滑度,对于恢复力的最大值几乎没有影响。
随着β和γ的取值不同,如图11所示,系统滞回恢复力具有软或硬的特性,β/γ为正值时,系统滞回恢复力具有软的特性,即滞回环的斜率比较小;β/γ为负值时,系统滞回恢复力具有硬的特性,即滞回环的斜率比较大。当β/γ的比值比较大时,系统滞回恢复力曲线包含的面积比较大,曲线形状比较饱满,这时系统在振动过程中耗能多;当β/γ的比值比较小时,系统滞回恢复力曲线包含的面积比较小,曲线形状比较瘦小,这时系统在振动过程中耗能少。当β=0,γ=0时,系统为线性系统,此时系统的滞回环面积为零,表示系统不耗能,系统的恢复力和位移都达到最大值。参数β,γ直接影响系统的非线性刚度和非线性阻尼的特性;β<γ时系统的耗能大于β>γ时的系统耗能。
随着γ值的不断减小,结构的滞回环形状从类似于正切函数的形状逐渐转变为类似于函数y=x3的形状;其中γ可为负值,当γ为负值时,曲线的形状呈细长状,并且在相同位移的情况下恢复力的值明显增大。该情况适用于钢筋混凝土桥墩受弯的滞回模型。随着β值不断地减小,导致滞回环的面积也随之减小,耗散能力降低,当β小于零时,系统反应不收敛,无法得到系统的滞回环。
图12表示强度退化系数改变时滞回曲线的变化情况,从图中可以看出,随着强度退化参数值的增加,每一滞回环强度退化程度随之增加。
图13表示刚度退化系数改变时滞回曲线的变化情况,从图中可以看出,随着刚度退化参数值的增加,每一滞回环刚度退化程度随之增加,即滞回环斜率递减;同时,刚度的退化会在一定程度上引起强度的退化。
本文提出的光滑滞回模型的控制参数有11个,其中有6个是控制的捏拢效应的,并且这6个参数具有明确的几何意义。
从图14中可以看出,随着滑移距离参数值的增加,滞回曲线呈现明显的倒“S”形表明此时存在较大的剪切、滑移影响。图15表示捏缩量级参数值变化的滞回曲线,随着该参数值的增大,滞回曲线呈现明显的捏缩现象,滞回环的面积随之减小,表征耗能能力降低。
根据图16,17和18,捏拢比率、捏拢率和捏拢斜率参数值的变化对滞回曲线的影响较小。根据图19可以看出,捏拢开始参数控制着滞回曲线出现捏拢开始的早晚,q值越大出现的捏拢的时间越晚,同时使滞回环变饱满,耗能能力增大。

图10 参数n值变化的滞回曲线Fig.10 Hysteresis curves variation with parameter n value

图11 参数β和γ变化的滞回曲线Fig.11 Hysteresis curves variation with parameters β and γ

图12 强度退化参数δν变化的滞回曲线Fig.12 Hysteresis curves variation with strength degradation parameter δν

图13 刚度退化参数δη变化的滞回曲线Fig.13 Hysteresis curves variation with stiffness degradation parameters δη

图14 参数ζs变化的滞回曲线Fig.14 The parameter ζs changes hysteresis curves

图15 参数ψ变化的滞回曲线Fig.15 Hysteresis curves variation with parameter ψ

图16 参数λ变化的滞回曲线Fig.16 Hysteresis curvesvariation with parameter λ

图17 参数δψ变化的滞回曲线Fig.17 Hysteresis curves variation with parameter δψ

图18 参数p变化的滞回曲线Fig.18 Hysteresis curves variation with parameter p

图19 参数q变化的滞回曲线Fig.19 Hysteresis curves variation with parameter q
4 数值模拟与试验结果对比分析
强震作用下,RC桥墩的破坏形态主要表现为弯曲破坏、剪切破坏、弯剪破坏,扭转破坏及弯扭破坏等失效模式。以下分别以常见的弯曲破坏、扭转破坏和弯剪破坏的塑性耗能、延性、退化以及捏拢效应等特性为例对试验结果和数值仿真结果比较分析。
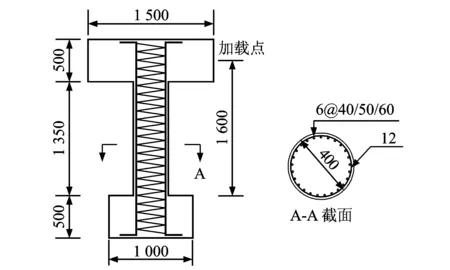
图20 试件几何尺寸和配筋图Fig.20 Specimen geometry and reinforcement
在恒定轴压的低周反复荷载试验中结构的恢复力如表达式(2)。弯曲破坏型钢筋混凝土桥墩的几何尺寸和配筋如图20所示,试件加载如图21所示,截面为圆形,其截面直径为400 mm,轴压比为0.1,配筋率为0.015,体积含箍率为0.006,图22给出了试验和数值分析得到的滞回曲线,从图中可以看出,数值仿真得到的曲线在峰值、刚度退化和强度退化等滞回性能上与试验测得的滞回曲线能够较好的吻合,其每一滞回环峰值的误差不超过10%。

图21 试件加载图Fig.21 The picture of specimen loading

图22 弯曲试验与模拟结果Fig.22 The test and numerical simulation results under bending
耗能是抗震性能的重要指标,运用对比分析耗能指标验证开发模型的有效性。耗能指标越高,说明结构在地震过程中消耗的地震能量越多,对结构的抗震安全性越有利,反之,则抗震安全性越差。该模型与试验耗能对比如图23所示,滞回环逐渐变得饱满,仿真模型耗散能量很接近试验结果。

图23 耗散能量Fig.23 Cumulative energy dissipation
扭转破坏类型的钢筋混凝土桥墩试验构件与弯曲破坏类型的构件几何尺寸及配筋和构造都相同,图24中实线显示,破坏有明显的捏拢现象,在数值分析中,通过辨别确定控制捏拢滑移的相关参数,模拟得到滞回曲线图24中虚线,试验滞回曲线与得到的仿真曲线各个特征吻合的都比较好,特别是捏拢效应。该模型与试验耗能对比如图25所示,模型耗散能量与试验结果误差不超过20%。
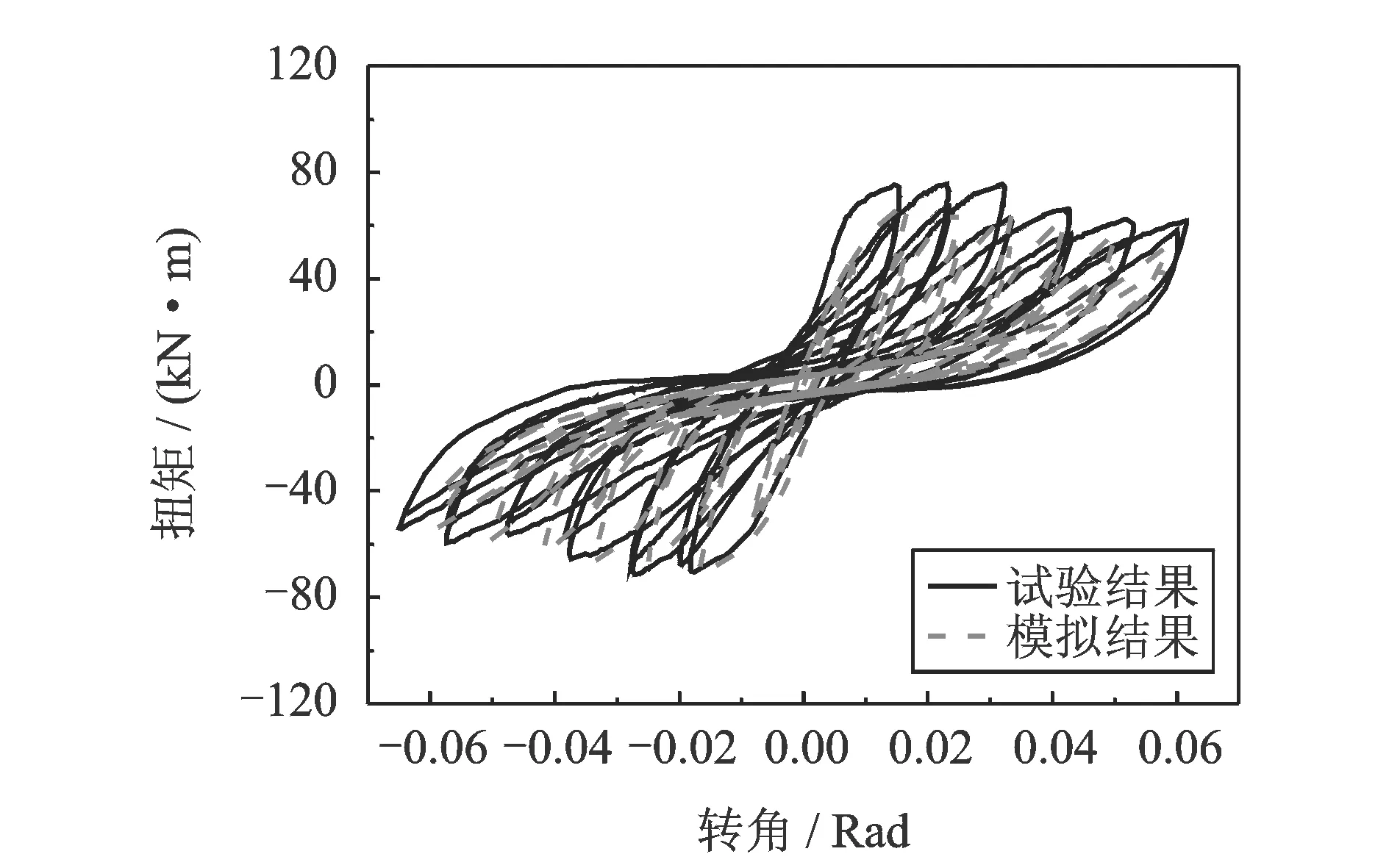
图24 扭转试验与数值结果Fig.24 The test and numerical simulation results under torsion

图25 能量耗散Fig.25 Cumulative energy dissipation
根据试验得到的力与位移关系的滞回曲线,对上述滞回模型相关参数进行调整,使之更加符合钢筋混凝土桥墩在地震作用下的反应,结果表明该滞回模型可较好的模拟不同破坏模式下钢筋混凝土桥墩的滞回性能,RC桥墩在弯曲破坏类型下误差小于10%,而扭转反应相差较大,也不超过15%。
弯剪破坏型钢筋混凝土桥墩几何尺寸和配筋如图26所示,轴压比为0.65,剪跨比为2.64,配筋率为0.015 8,体积含箍率为0.007 9,图27给出了试验和数值仿真得到的滞回曲线,从图中可以看出,数值仿真得到的滞回曲线和试验得到的滞回曲线吻合较好,特别是当达到屈服后刚度和强度退化逐渐明显的特征吻合的基本一致。每一滞回环的误差不超过20%,试验结果与数值仿真结果的耗能对比如图28所示,能量耗散误差控制在15%内。

图26 试件几何尺寸和配筋图Fig.26 Specimen geometry and reinforcement

图27 弯剪试验与数值结果Fig.27 The test and numerical simulation results under torsion
3种破坏模式下模拟时所采用相应参数的确切值如表1所示。上述各试验和模拟结果证实了本文改进的Bouc-Wen模型能比较好地模拟RC桥墩在拟静力试验中的滞回曲线。但拟静力试验,不能考虑试件应变速率影响所产生的变化,从而不能反映地震对RC桥墩的真实影响。以下采用Bouc-Wen模型对其在实际地震作用下RC桥墩的非线性滞回性能进行了分析。

表1 模拟所采用相应参数的确切值
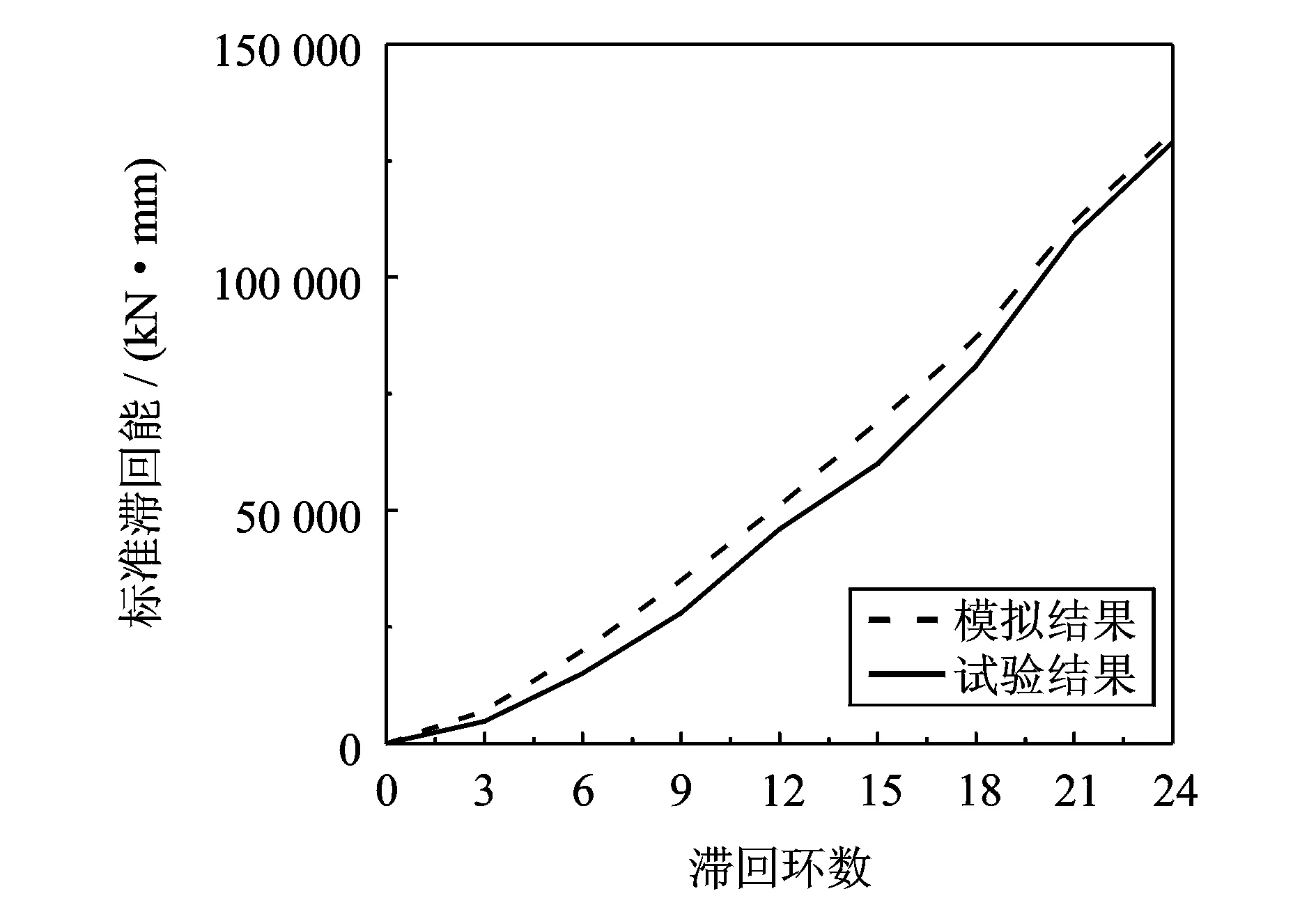
图28 能量耗散Fig.28 Cumulative energy dissipation
在2008年汶川地震中,绵竹市回澜立交桥匝道桥的RC桥墩,在地震中损伤破坏严重[17]。汶川地震波激励下,该匝道桥某RC桥墩的力和位移反应的滞回曲线,如图29所示,数值模拟得到的滞回曲线随着外激励的持续,滞回环的形状趋于饱满,结构的非线性损伤程度不断地增大,也验证Bouc-Wen模型的适用性和通用性。因此,给出的模型可以较好地模拟结构在地震作用下的非线性损伤时域演化特征。
5 改进的Bouc-Wen模型中参数识别的应用
当模型选定后,接下来需要解决的问题是如何根据试验数据辨识出模型中的参数。由于Bouc-Wen模型是一个复杂的非线性模型,非线性滞回系统的参数识别难点就在于问题的非线性和双值性,其参数识别存在一定的难度,也是一个研究的热点,参数识别的正确与否是模型能否准确描述非线性滞回特征的关键。对于不同的工程情况,参数识别方法也不同。根据Bouc-Wen模型的非线性和双值性,本文采用无迹卡尔曼滤波(UKF)的方法对其进行参数识别。
首先考虑一个单自由度非线性滞回系统在以汶川地震波作为外部激励的作用下,运用无迹卡尔曼滤波对该模型进行识别分析,引入一个增加的状态向量用公式表示状态空间方程
(17)
状态空间方程为
(18)
式中:

u(t)是已知的输入地震外激励力。如果加速度反应和外部激励可以被测,则测量方程可以表示成
(19)
式中ν为测量噪音,在本文中考虑Gaussian白色噪音。
UKF算法在计算之前需要给定一个状态初值和协方差矩阵初值以启动循环。初值的给定方法很多,其效果也大致相同,因为UKF对初值的选定要求并不严格,只需要大致接近真实值即可。
在本例中参数初始值如表2所示,在外部激励力为汶川地震波的作用下,通过计算可以得到系统反应的位移,速度,加速度。为了探索识别的鲁棒性,噪声、白噪声过程噪声信号均方根为2%,模拟加速度回应地震地面加速度。一个代表时间历程的一些确定参数如图30所示。最后的估计值的参数和对应百分比误差在表2中所示。从表中可以得到,参数估计的平均误差大约是4.5%,最大的估计误差是8%(参数)。识别结果表明UKF方法跟踪状态和模型参数的退化滞后系统好。

图29 RC桥墩在汶川地震作用下滞回性能Fig.29 Hysteresis behavior of RC bridge pier under Wenchuan earthquake excitation

图30 系数的估计结果Fig.30 Estimates of parameter

表2 退化系统的参数估计
6 总 结
本文基于Bouc-Wen微分滞回模型,给出了一种适用于钢筋混凝土桥墩的改进滞回模型,该模型综合考虑了刚度退化,强度退化和捏拢效应,通过对该改进滞回模型控制参数识别,运用数值模拟得到钢筋混凝土桥墩在不同破坏模式下的滞回曲线,并与拟静力试验所得的滞回曲线进行了对比分析。对比结果显示,模型的峰值,刚度、强度退化和捏拢效应等滞回性能特征与试验都能较好的吻合,尤其是反映在RC桥墩发生扭转破坏时产生的捏拢效应。基于该改进模型,分析了RC桥墩在实际地震作用下的滞回特性,得到良好的效果。因此,该修改的滞回模型可以较好地模拟RC桥墩在地震作用下的非线性损伤时域演化特征。在此基础上,运用无迹卡尔曼方法对Bouc-Wen模型进行参数估计,模拟结果和误差分析表明,无迹卡尔曼(UKF)算法能够精确的估计出非线性Bouc-Wen模型的参数。
致谢:美国The State University of New York at Buffalo多学科地震工程研究中心(MCEER)的Jianwei Song 教授和George C. Lee教授在研究思路和定稿过程中提出了许多宝贵意见,作者对此表示衷心感谢!
[1] 梁建术,蔡建军.一类含间隙滞回动力系统周期运动和分岔[J].机械强度,2007,29(3):390—393.
Jianshu Liang, Jianjun Cai. Periodic motions and bifurcation sofa class of hysteretic dynamics with gaps[J]. Journal of Mechanical Strength, 2007,29(3):390—393.
[2] 白鸿柏,黄协清.基础柔性对干摩擦隔振系统影响作用研究[J].机械强度,1999,21(1):22—25.
Hongbai Bai, Xieqing Huang. Study of influence of flexible foundation on dry friction damped isolation system[J]. Journal of Mechanical Strength, 1999,21(1):22—25.
[3] Hong S R, Choi S B, Choi Y T, et al. A Hydro-mechanical model for hysteretic damping force predictionof ER damper: experimental verification[J]. Journal of Sound and Vibration, 2005,285(4-5):1 180—1 188.
[4] Sivaselvan M, Reinhorn A. Hysteretic models for deterioration inelastic structures[J]. ASCE Journal of Engineering Mechanics, 2000,126(6):633—640.
[5] Clough R W. Inelastic earthquake response of tall buildings[A]. Proceedings of the 3rd World Conference on Earthquake Engineering[C]. New Zealand, 1965:68—89.
[6] Takeda T, Sozen M A, Nielsen N N. Reinforced concrete response to simulated earthquakes[J]. ASCE Journal of Structural Division, 1970:2 557—2 573.
[7] Saiidi M A Sozen. Simple nonlinear seismic analysis of RC structures[J]. ASCE Journal of Structural Engineering, 1981,107(5):937—952.
[8] Bouc R. Force vibration of mechanical systems with hysteresis[A]. In Proceedings of the Fourth Conference on Nonlinear Oscillation[C]. Prague, Czechoslovakia, 1967,315.
[9] Wen Y K. Method for random vibration of hysteretic systems[J]. ASCE Journal of Engineering Mechanics, 1976,102(2):249—263.
[10]Baber T T, Wen Y K. Random vibrations of hysteretic degrading systems. Journal of Engineering Mechanics[J]. ASCE Journal of Engineering Mechanics, 1981,107(6):1 069—1 089.
[11]Baber T T, Noori M N. Random vibration of degrading pinching systems. Journal of Engineering Mechanics[J]. ASCE Journal of Engineering Mechanics, 1985,111(8):1 010—1 026.
[12]Ma F, Zhang H, Bockstedte A, et al. On parameter analysis of the differential model of hysteresis[J]. ASME Journal of Applied Mechanics, 2003,71(3):257—268.
[13]Baber T T, Noori M N. Modeling general hysteresis behaviour and random vibration Applications[J]. Journal of Vibration, Acoustics, Stress and Reliability in Design, 1986,108(4):411—420.
[14]李鸿光,何旭,孟光.Bouc-Wen滞回系统动力学特性的仿真研究[J].系统仿真学报,2004,16(9):2 009—2 011.
Li Hongguang, He Xu, Meng Guang. The esearch of Bouc-Wen hysteretic system dynamic simulation[J]. Journal of System Simulation, 2004,16(9):2 009—2 011.
[15]Wu Meiliang, Andrew Smyth. Real-time parameter estimation for degrading and pinching hysteretic models[J]. International Journal of Nonlinear Mechanics, 2008,43(9):822—833.
[16]Foliente G C. Hysteresis modeling of wood joints and structural systems[J]. ASCE Journal of Engineering Mechanics, 1995,121(6):1 013—1 022.
[17]Han Qiang, Du Xiuli, Liu Jingbo. The seismic damage of highway bridges during 2008 Wenchuan earthquake[J]. Earthquake Engineering and Engineering Vibration, 2009,8(2):263—273.
Hysteresis model and parameter identification of RC bridge piers considering strength and stiffness degradation and pinching effect
HANQiang,DONGHui-hui,GUOJie
(Key Laboratory of Urban Security and Disaster Engineering of MOE,Beijing University of Technology, Beijing 100124, China)
In order to effectively simulate the nonlinear hysteresis behavior of reinforced concrete (RC) bridge piers under strong earthquake excitation, an improved nonlinear hysteresis model for RC bridge piers was developed and its controlling parameters were determined considering stiffness and strength degradation and pinching effect based on classical Bouc-Wen model. The improved model can be carried out to predict the nonlinear hysteresis behavior of RC bridge piers under various failure modes using MATLAB/ Simulink program. Cyclic tests of different failure mode bridge column specimens were performed under constant axial load with lateral bending. The results did show that force-displacement relationship curves of bridge column specimens derived from theoretical analysis agree well with the experimental results. The nonlinear hysteresis behavior of bridge column specimen was simulated under 2008 Wenchuan earthquake excitation and its failure modes were identical with the real earthquake damage of bridge column. The improved analytical models in the paper were applied to accurately predicting the nonlinear hysteresis behavior of RC bridge columns with strength and stiffness degradations and the pinching effect subjected to strong earthquake motion. Unscented Kalman filter (UKF) was applied to estimate the parameters of Bouc-Wen model in this paper, the simulation results and error analysis show that the method can accurately estimate the parameters of improved Bouc-Wen model.
RC bridge column; hysteresis model; stiffness and strength degradation; pinching effect; parameter identification
2013-08-01;
2014-08-04
国家自然科学基金资助项目(51178008);北京市自然科学基金资助项目(8122003);长江学者和创新团队发展计划资助项目(IRT13044)
TU375.3
A
1004-4523(2015)03-0381-13
10.16385/j.cnki.issn.1004-4523.2015.03.007
韩强(1974—),男,博士,副教授。电话:(010)67392500;E-mail:qhan@live.com
