瞬变电磁法数值模拟实验教学软件研究

2015-05-08昌彦君肖明顺

实验技术与管理 2015年7期

昌彦君, 张莹, 肖明顺

(1. 中国地质大学(武汉) 地球物理与空间信息学院, 湖北武汉 430074；2. 中国地质大学(武汉) 地球内部多尺度成像湖北省重点实验室, 湖北武汉 430074； 3. 中国冶金地质调查局中南地勘院, 湖北武汉 430074)

瞬变电磁法数值模拟实验教学软件研究

昌彦君1,2, 张莹1, 肖明顺3

瞬变电磁法是一种广泛应用于矿产资源、水资源、工程与环境地质调查的地球物理方法。由于电磁场偏微分方程的求解十分复杂,使得其理论教学过程非常费时。该文以提高教学效果为目的开发出瞬变电磁法数值模拟实验教学软件。该教学软件包括网格剖分模块、有限元计算模块、GS系数循环模块,傅氏系数循环模块等,通过按数值计算流程图的演示,使得学生更容易理解。数值模拟实验教学软件简化了教学过程,节约了教学时间,具有生动形象和易于理解的教学效果。

瞬变电磁法；数值模拟实验； 2.5维正演；教学软件

瞬变电磁法(transient electromagnetic method,TEM)是一种广泛应用于矿产资源、水资源、工程与环境地质调查的地球物理方法[1-2]。由于TEM的应用广泛,目前许多大学都开设了关于TEM的基础理论和应用技术课程。在瞬变电磁法的理论教学中,电磁场偏微分方程的求解十分复杂[3],尤其是复杂模型条件下的数值模拟,教学过程非常费时[4]。实验教学软件不仅可以简化教学过程,而且具有生动形象和易于理解的教学效果[5],因此,开发一套瞬变电磁法数值模拟实验教学软件,对于提高瞬变电磁法课程的教学效果具有重要的意义。笔者基于多年科研成果[6-8],以实验教学为目的,开发出瞬变电磁法数值模拟实验教学软件,通过数值计算流程图的演示,使学生更容易理解复杂模型情况下的数值求解过程。

1 瞬变电磁法数理方程及其求解

瞬变电磁法的数值模拟内容包括一维、二维、2.5维(二维地电模型和三维场源)和三维问题。由于一维问题相对简单,二维问题不符合实际的三维源性质,三维问题涉及的计算量过大,因而在科研中常选择介于二维和三维之间的所谓2.5维问题进行正演理论的研究[9-11]。相对三维,2.5维的计算量显著减少；相对二维,2.5维能更好地接近野外实际地质情况。因此,本文探讨的瞬变电磁法数值模拟实验教学软件也是基于2.5维模型开发的。

在三维各向同性均匀导电介质中，电(磁)偶极子形成的电磁场满足Maxwell方程。在时间域中，有如下方程组：

在介质分界面上，满足衔接条件：

其中,ε为介电常数，σ为电导率，μ为磁导率, Γ为介质分界面，n为分界面的法向方向矢量。E为电场矢量，H为磁场矢量；Je为场源电流密度矢量，Jm为场源磁流密度矢量。以下标1和2表示不同的介质。

电(磁)偶极子源位于笛卡尔坐标原点时，有

其中，δ(x)、δ(y)和δ(z)为狄拉克(Dirac)源函数；Pe、Pm分别为源的电偶极矩和磁偶极矩，且有Pe=IΔs，Δs为电流元长度，Pm=IS，S为小电流环的面积；μ0是真空中的磁导率；I为按阶跃规律变化的供电电流强度，它满足下式:

瞬变电磁法三维正演问题为时间(t)和空间(x,y,z)域的四维复杂问题。所谓的2.5维问题，是三维问题的一个特例，即二维地电模型(模型的电、磁性参数在地质体走向方向无变换)和三维场源。求解时，利用拉普拉斯变换对时间(t)消维，将时空(t,x,y,z)域四维问题转换为离散的拉普拉斯域的(x,y,z)三维问题；对走向(y)方向电磁场分量作傅里叶变换，进一步降维得到离散的拉普拉斯和傅里叶域下的(x,z)二维问题；运用有限元单元法求解二维问题，通过反傅里叶变换和逆拉普拉斯变换得到时空(t,x,y,z)域电磁场响应，这便是时间域有源电磁法2.5维有限元数值模拟的计算思路[11-12]。

2 算法流程及其功能模块

瞬变电磁法数值模拟算法流程图对学生理解瞬变电磁法的数值计算过程有很大帮助，该流程图反映了瞬变电磁法的核心计算原理和计算步骤，是整个数值模拟的精华和学习要点。图1为软件的计算流程图，各主要功能模块介绍如下。

图1 瞬变电磁法数值模拟算法流程图

(1) 网格剖分预处理模块。网格剖分预处理模块负责软件的主要GUI交互。运用有限单元算法求解离散的拉普拉斯和傅里叶域下的(x,z)二维问题，需要剖分地下计算区域网格，建立网格单元电性参数和几何参数信息，提供给用于数值计算的FORTRAN动态计算库。软件使用者仅仅需要提供测点信息和采样时间参数信息等，程序将自动剖分有限元网格，并提供GUI交互供软件使用者建立地电网格模型，划分异常地质体。软件并未解决2.5维瞬变电磁的全自动反演，仅仅提供了一种粗糙的人机联作试错反演。因此，正演和试错反演的网格剖分模块是一致的。

(2) 数据参数传递模块。数据参数传递模块负责软件向FORTRAN动态计算库的数据传输，即传输地下计算区域网格单元的电性和几何参数以及其他信息。由于瞬变电磁法数值模拟需要考虑空气因素的影响，实际计算的有限元网格需要包括向上拓展的空气网格，因此数据参数传递模块也负责扩充地下网格，形成适用于计算的计算网格。

(3) 有限元计算模块。有限元计算模块是FORTRAN动态计算库的核心模块，即计算拉普拉斯和傅里叶域下不同测点位置的(x,z)二维电磁场响应。FORTRAN动态计算库采用了Gaver-Stehfest逆拉普拉斯算法进行拉普拉斯逆变换[13]，一个时间点仅仅需要十几个拉普拉斯域的计算值。因此，2.5维瞬变电磁场响应的计算为时间、傅里叶系数、Gaver-Stehfest系数、场源测点位置的四重循环。

(4) 源点循环模块。源点循环是时间、傅里叶系数、Gaver-Stehfest系数、场源测点位置四重循环的最里层循环。上述有限元计算到最后归结于一个线性方程组的求解。在相同的地电模型参数、相同的采样时间、发射线圈参数和一定的近似条件下,不同测点的有限元线性方程组有相同的计算部分。因此,将源点循环放在四重循环最里层,可减少重复计算量。

(5) GS系数循环模块。GS系数循环即Gaver-Stehfest系数循环。由于Gaver-Stehfes逆拉普拉斯变换算法对精度要求很高[14],因此,将其放在第三层循环。

(6) 傅氏系数循环模块。傅氏系数循环即傅里叶系数循环。通过Gaver-Stehfes逆变换得到不同的采样时间、不同的测点位置、不同的傅里叶系数下的二维电磁场响应之后,运用数值计算实现傅里叶反变换,得到不同的采样时间、不同的测点位置下的空间域电磁场响应值。

(7) 数据传递输出模块。数据传递输出模块负责FORTRAN动态计算库的数据传输,即传输瞬变电磁场响应值,并调用相关计算模块得到视电阻率、视深度等辅助信息。该模块亦负责数据的图形显示,包括视电阻率拟断面图和磁感电动势多测道剖面图等。

3 实验教学软件的部分演示

软件的开发是基于VC6.0平台进行的,采取界面GUI开发和数值计算核心剥离开发的思路,以便于增加新的计算模型,以及根据教学需要不断地完善与扩充内容。瞬变电磁法数值模拟实验教学软件的部分功能演示如下:

(1) 导入测点数据；(2)选择测点数据(见图2)；(3)形成网格(见图3)；(4)选择矩形工具并用鼠标左键画矩形；(5)右键点击赋予电性参数(见图4)；(6)正演计算(见图5)；(7)查看视电阻率断面图(见图6)。

图3 形成网格界面

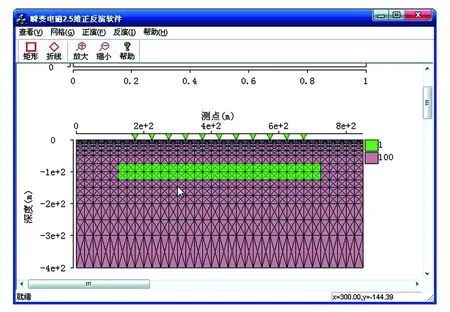
图4 赋予电性参数界面图

图5 正演计算页面

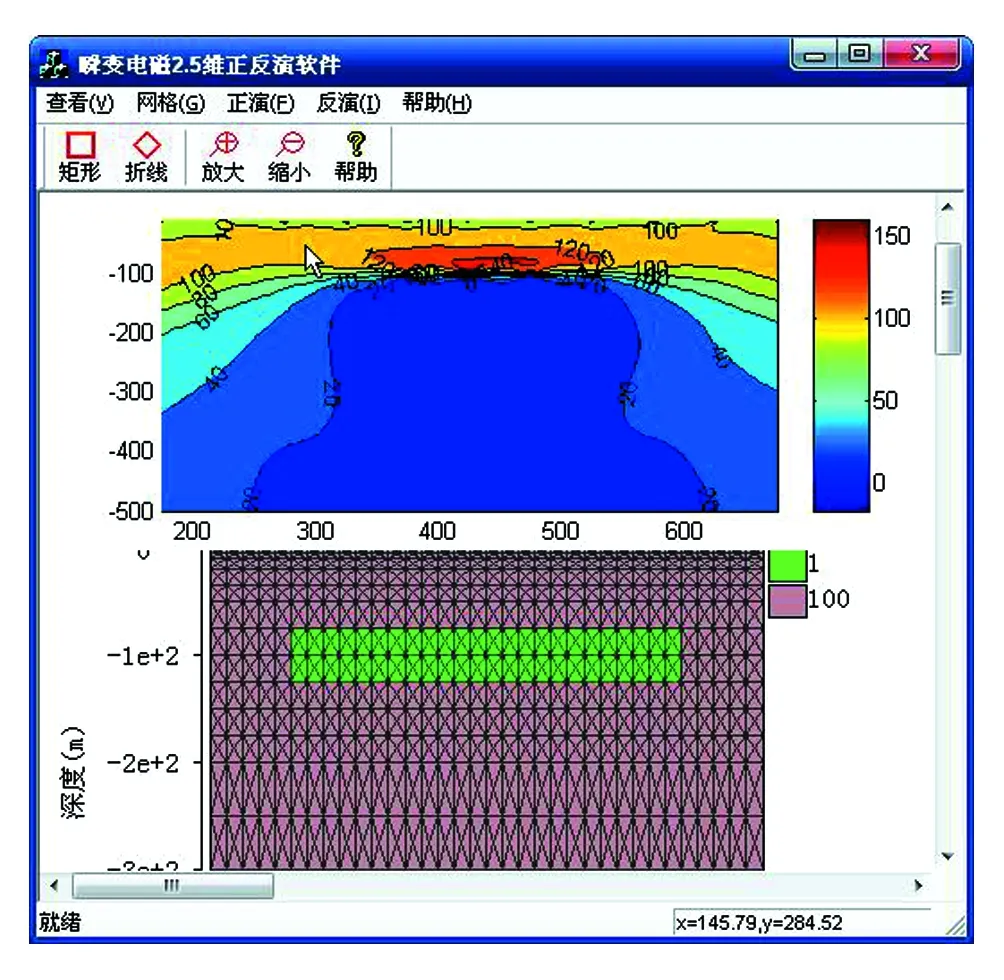
图6 视电阻率断面图

4 结束语

通过数值模型和计算流程图,将复杂的电磁场偏微分方程的求解过程形象化,使得瞬变电磁法课程的教学过程得到了简化。软件中储存的大量常用模型的数值计算结果,极大地丰富了教学内容,缩短了授课时间。对于复杂且不容易理解的教学内容,通过使用数值模拟实验教学软件,不但提高了教学效果,也激发了学生的学习兴趣,促使学生从被动学习转变为主动学习,这种教学方法值得进一步完善和推广。

References)

[1] 陈载林,黄临平,陈玉梁.我国瞬变电磁法应用综述[J].铀矿地质,2010,26(1):51-54.

[2] 郭宁宁,昌彦君.瞬变电磁法在城区建筑基坑中的防空洞探测[J].工程地球物理学报,2011,8(6):705-708.

[3] 蒋邦远.实用近区磁源瞬变电磁法勘探[M].北京:地质出版社,1998.

[4] Wannamaker P E,Hohmann G W,Sanfilipo W A.Electromagnetic modeling of three-dimensional bodies in layered earths using integral equations[J].Geophysics,1984,49(1):60-74.

[5] 昌彦君,张莹,曹中林.探地雷达数值模拟实验研究[J].实验技术与管理,2009,26(4):69-72.

[6] 昌彦君,张桂青.电磁场从频率域转换到时间域的几种算法比较[J].物探化探计算技术,1995(3):25-29.

[7] 昌彦君,肖明顺,武毅.瞬变电磁数据一维反演时的初值选取研究[J].石油地球物理勘探,2010,45(2),295-298.

[8] 昌彦君,肖明顺,孟永良,等.带地形的瞬变电磁2.5维有限元数值模拟研究[G]//地球物理科学研究十年进展论文集.武汉:中国地质大学出版社,2012:267-278.

[9] Mitsuhata Y.2-D electromagnetic modeling by finite-element method with a dipole source and topography[J].Geophysics,2000,65(2):465-475.

[10] 孟永良,罗延钟,昌彦君.时间谱电阻率法的二维正演算法[J].地球科学,2000,25(6):656-662.

[11] 王华军,罗延钟.中心回线瞬变电磁2.5维维有限元算法[J].地球物理学报,2003,46(6):855-862.

[12] 徐世浙.地球物理中的有限单元法[M].北京:科学出版社,1994.

[13] Knight J H,Raiche A P.Transient electromagnetic calculation using the Gaver-Stehfest inverse Laplace transform method[J].Geophysics,1982,47(1):47-50.

[14] 罗延钟,昌彦君.G-S变换快速算法[J].地球物理学报,2000,43(5):684-690.

Research on teaching software of numerical simulation of transient electromagnetic method

Chang Yanjun1,2, Zhang Ying1, Xiao Mingshun3

(1. Institute of Geophysics and Geomatics,China University of Geosciences,Wuhan 430074,China; 2. Subsurface Multi-scale Imaging Laboratory,China University of Geosciences,Wuhan 430074,China; 3. Zhongnan Institute of Geological Exploration,China Metalurgical Geology Bureau,Wuhan 430074,China)

The transient electromagnetic method (TEM) is a kind of tool used widely in mineral and oil exploration as well as water exploration,engineering and environment geophysics exploration.Its theory teaching process is very time-consuming due to the complexity of the solution of electromagnetic field partial differential equations.This paper develops the numerical simulation experiment teaching software of the transient electromagnetic method for the purpose of experiment teaching based on scientific research.The teaching software modules,including grid subdivision finite element calculation module,GS coefficient circulation module,Fourier coefficient circulation module and so on,make students easy to understand by demonstrating the flow chart of numerical calculation. It may not only simplify the teaching process and save the teaching time, but also have good teaching effect of vivid image and easy to understand.

transient electromagnetic method; numerical simulation experiment; 2.5-dimensional forward; teaching software

2014- 11- 25 修改日期：2015- 01- 07

中国地质大学创新实验和地球内部多尺度成像湖北省重点实验室基金项目资助

昌彦君(1964—),男,湖北仙桃,博士,教授,主要从事电磁法勘探的数值模拟研究.

P631

1002-4956(2015)7- 0131- 04