基于局部线性嵌入的时间序列聚类
2015-05-08翁小清
刘 学,翁小清
(河北经贸大学信息技术学院,河北 石家庄 050061)
聚类就是将未标记的实例对象根据它们之间的相似度进行分组,使组内实例之间的相似度最大,而组与组之间的实例相似度最小,以达到发现隐藏在数据中的内部结构的目的。时间序列[1]通常是一种高维且随着时间变化而变化的数据,它的产生过程极易受环境因素的影响,并且存在一定的噪声。时间序列聚类广泛应用于金融、交通、医学、手势识别等领域。
时间序列一般维数很高,为了可以有效的进行时间序列聚类,通常需要将样本的维数进行约简。如今维数约简的方法有很多,比如,小波、傅里叶变换、主成分分析[2](Principal Component Analysis,PCA)、分段聚合近似[3,4](Piecewise Aggregate Approximation,PAA)等。PCA是将多个关联变量转化为几个非关联的综合变量,在现实中数据集往往具有非线性的特征,而PCA属于线性维数约简方法,由于PCA的这种线性局限性,使得它对具有非线性结构的数据集映射效果不好。PAA是通过对时间序列进行平均分割并利用分段序列的均值来表示原时间序列特征的方法,但是它没有考虑数据集中各时间序列样本之间的内在关系。局部线性嵌入[5](Locally Linear Embedding,LLE)是一种非线性维数约简方法,利用局部线性嵌入映射来逼近全局的非线性流形。LLE使得在高维空间中相邻的点映射到低维空间之后应该也是相邻的。
本文提出了一种基于LLE的时间序列聚类方法,首先使用LLE对时间序列样本维数约简,在低维空间对维数约简后的数据进行聚类,将它的聚类性能与已有方法如PCA、PAA进行了比较,对实验结果进行配对样本t检验,实验结果表明,本文提出的方法更能提高聚类性能。
1 局部线性嵌入
LLE是由Sam T.Roweis和Lawrence K.Saul提出的一种非线性降维方法。LLE的基本思想是:利用局部线性嵌入映射来逼近全局的非线性流形。在由高维空间向低维空间嵌入的过程中,流形上每个点的局部结构不变,LLE是通过使用它的近邻点重构这个点来实现的。
对于LLE算法,我们给一个简单的介绍[6]。已知原始数据集X= {x1,x2,…,xn}⊂Rl,对每个点xi,找到它的k近邻。计算每个点与它的近邻点之间的权重wij,即最小化误差函数:

其中,xj是xi的第j个邻域,wij表示xi与xj之间的权重,N是数据集中点的个数=1,当xj不是xi的k近邻时,wij=0。
使用上一步的重构权重,计算xi在低维空间的嵌入yi。最小化下面的代价函数可以得到低维空间向量:

为了使低维数据均匀分布,对y进行规范化限制。其中其中O是每一个分量都为0的列向量,I是单位矩阵。
2 基于LLE的时间序列聚类算法
提出的基于LLE的时间序列聚类算法包括三步:首先,对每个样本点求它的k个近邻点;其次,由每个样本点的k个近邻点计算出该样本的局部重构权值矩阵W;最后,根据W和近邻点计算出样本在低维空间的嵌入。
LLE聚类算法描述:
输入:数据集,Data,近邻个数,k,嵌入维数,d,聚类个数,M
输出:聚类结果
Step1:使用PCA对数据集进行预处理,去掉噪声,保留原数据集的主要信息。
Step2:对每个点xi,找到它的k近邻。
Step3:计算每个点xi的重构权重Wi,使误差函数(1)最小。
Step4:使用上一步的重构权重Wi,计算xi在低维空间的嵌入yi,使得代价函数(2)最小,由此得到降维后的矩阵Y。
Step5:使用K均值聚类,将Y聚成M个类。
算法分析:
用N表示数据集中样本个数,每个样本用一维向量来表示,输入样本的维数为D。在第一步中,使用PCA对数据集进行预处理的时间复杂度[7]为O(ND2)。LLE的复杂度分为三部分:一是k近邻搜索。二是计算权值wij。三是计算低维嵌入值Y。在k近邻搜索中,复杂度为O(DN2)。在计算权值wij时,复杂度为O(DNK3),其中,K为近邻个数。在计算低维嵌入值Y时,复杂度为O(dN2),其中,d为所嵌入的维数。因此,LLE算法的复杂度[8]为O((D+d)N2+DNK3)。K均值聚类的复杂度[9]是O(hNM),其中,h为迭代次数,M为簇数,即聚类个数。所以算法的复杂度为O((D+d)N2+DN(K3+D)+hNM)。
3 实验
在10个时间序列数据集上,对本文提出的基于LLE的聚类算法的性能进行了测试,并与使用PCA和PAA进行K均值聚类的性能进行了比较。在实验中,采用micro-p(micro-precision)[10,11]度量聚类的性能。使用不同参数时,聚类的micro-p值可能不同,在此只给出了各种方法的最高的micro-p值以及相应的参数。下面分别对实验数据、比对的算法以及实验的结果进行介绍。
3.1 数据集描述
本实验在10个时间序列数据集[12]上进行了测试,这些数据集来自医学、手势识别、化学、生物信息等领域。表1列出了这10个数据集的主要特征,包括类别个数、样本总数以及时间序列的长度。
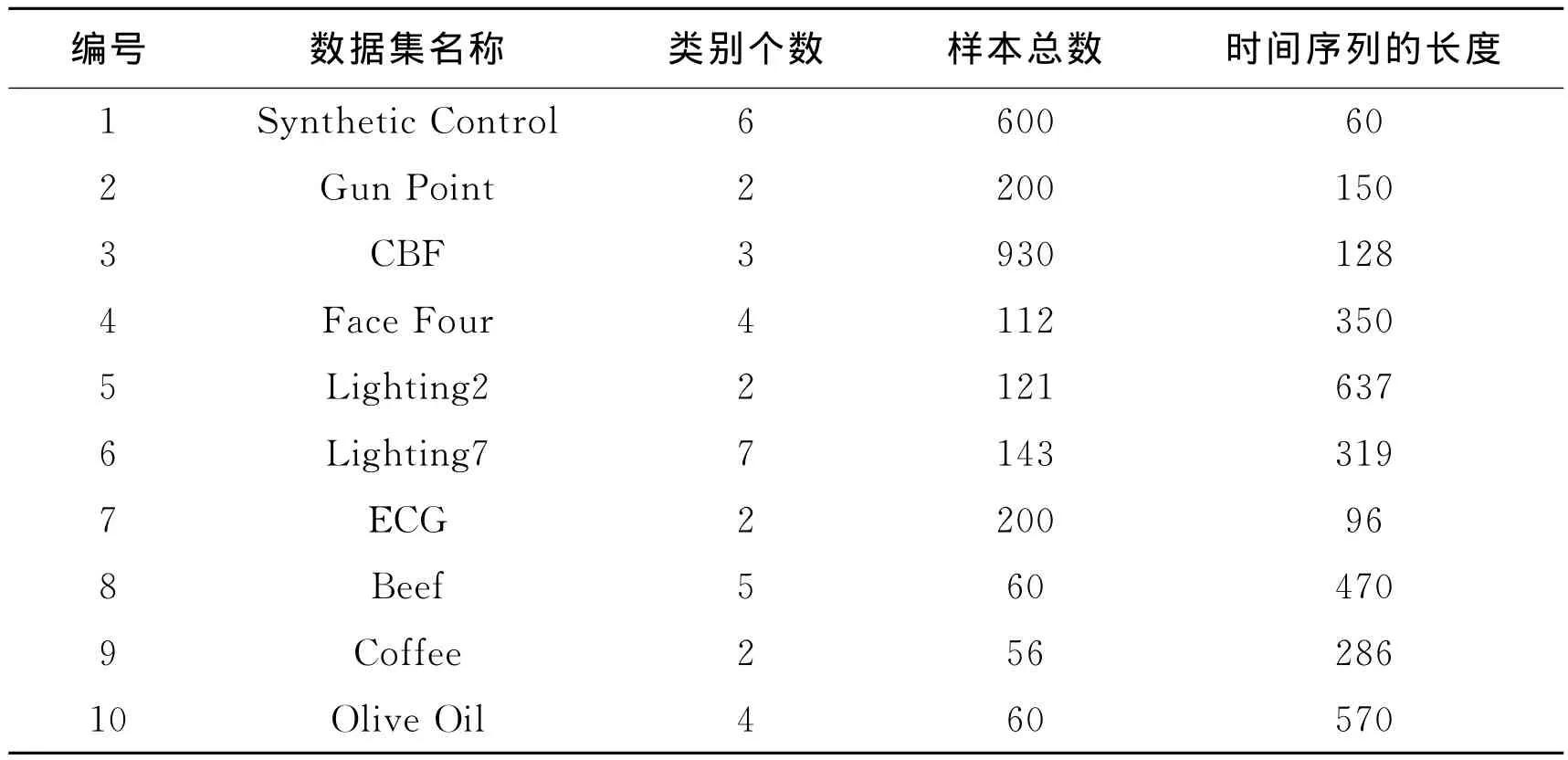
表1 数据集描述
3.2 评价准则
聚类性能用micro-p表示,在一个已经有已知类别的数据集中,假设数据集分为c类,{C1,C2,…,Cc}。通过聚类实验得到数据集中每个样本的类别标号。ah表示被正确分到类Ch中的样本的个数,n为数据集中样本个数。

3.3 性能比较
表2给出了在10个数据集上,分别使用原始数据,PCA,PAA以及LLE进行K-均值聚类的micro-p值;对于每一种测试都重复10次实验,然后记录下平均的micro-p值;第2列给出了在原始数据上直接进行K-均值聚类的micro-p值,第3列、第4列、第5列分别给出了使用PCA、PAA以及LLE进行聚类时最高的micro-p值以及相应嵌入空间的维数。
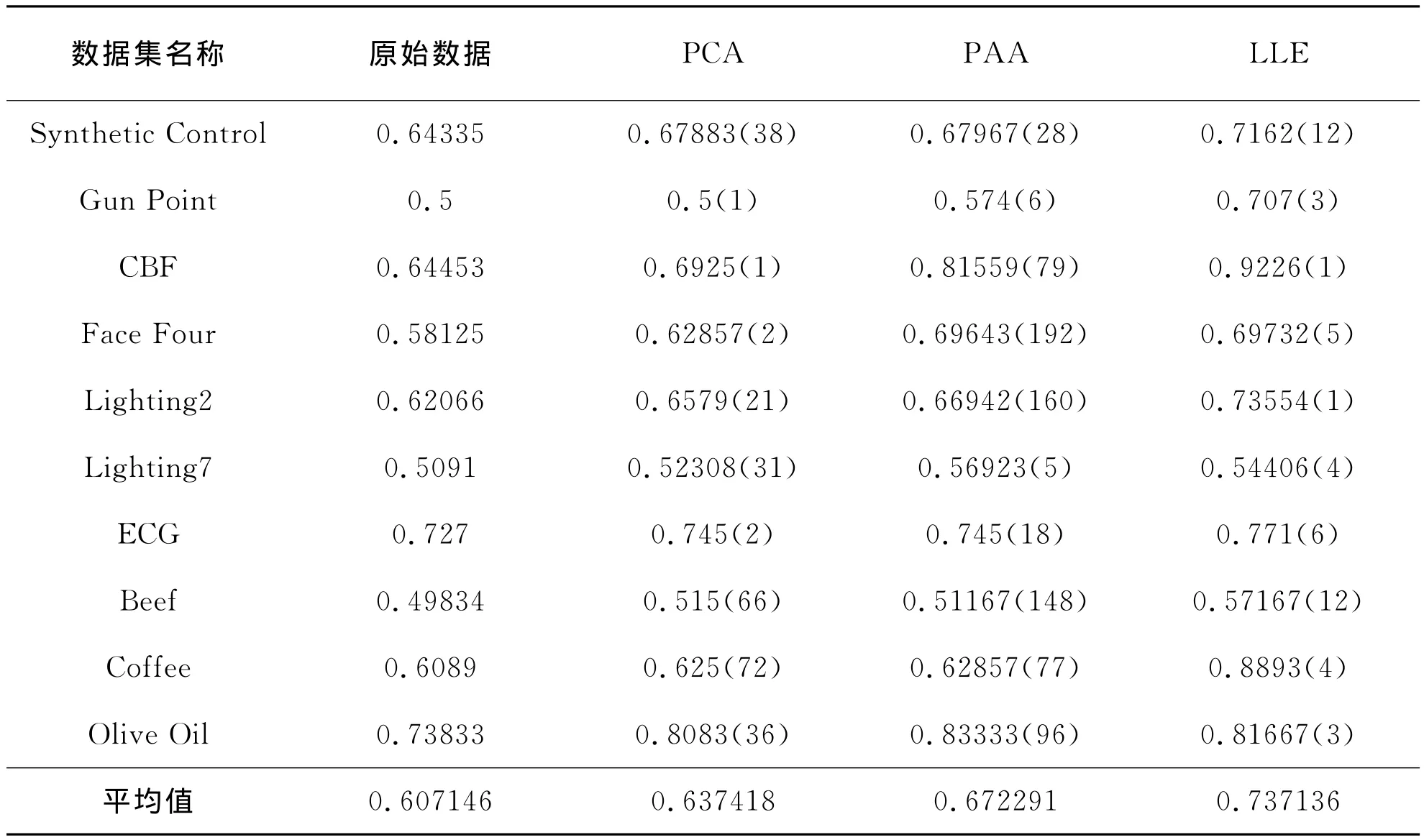
表2 三种维数约简算法聚类结果比较
为了对聚类结果的平均值进行显著差异的判断,我们采用配对样本t检验[13]。
它是根据样本数据对两个配对样本来自的两个配对总体的均值是否有显著差异进行判断。使用matlab对原始数据与LLE、PCA与LLE、PAA与LLE进行了配对样本t检验,计算出的t统计量值以及概率p值如表3所示。
从表2以及表3可以看到,原始数据与LLE的配对样本t统计量为-4.4595,概率p值为0.0016<0.05,说明使用LLE的聚类性能显著地好于直接在原始数据上进行聚类的聚类性能。在10个数据集上,使用LLE的平均micro-p值为0.737136,而原始数据的平均micro-p值为0.607146。

表3 配对样本t检验
PCA与LLE的配对样本t统计量为-3.2883,概率p值为0.0094<0.05,说明使用LLE的聚类性能显著地好于使用PCA的聚类性能。在10个数据集上,使用LLE的平均micro-p值为0.737136,而使用PCA的平均micro-p值为0.637418。
PAA与LLE的配对样本t统计量为-2.3952,概率p值为0.0402<0.05,说明使用LLE的聚类性能显著地好于使用PAA的聚类性能。在10个数据集上,使用LLE的平均micro-p值为0.737136,而使用PAA的平均micro-p值为0.672291。
3.4 参数对算法性能的影响
基于LLE的聚类算法,有两个参数,一个是嵌入维数d,另一个是近邻个数k。为了观察参数对算法性能的影响,我们先将近邻个数k固定,让嵌入维数d从1变化50。图1给出了在Coffee数据集上,将近邻个数k固定为25,micro-p随嵌入维数d的变化情况;图2给出了在Gun Point数据集上,将近邻个数k固定为5,micro-p随嵌入维数d的变化情况。从图1和图2可以看到,当嵌入维数d比较小时,micro-p有一个快速上升和快速下降的过程,之后趋于平缓。由此可以看出本文提出的基于LLE的时间聚类方法,并不需要很高的嵌入维数就可以获得不错的聚类效果。

图1 在Coffee数据集上micro-p随嵌入维数变化情况

图2 在Gun Point数据集上micro-p随嵌入维数变化情况
将嵌入维数d固定,让近邻个数k从1变化50。图3给出了在ECG数据集上,将嵌入维数d固定为6,micro-p随近邻个数k变化情况;图4给出了在GunPoint数据集上,将嵌入维数d固定为3,micro-p随近邻个数k变化情况。从图3和图4可以看到,随着近邻个数k的增加,micro-p的值在一定范围内波动,比较稳定,近邻个数k对聚类性能的影响较小。
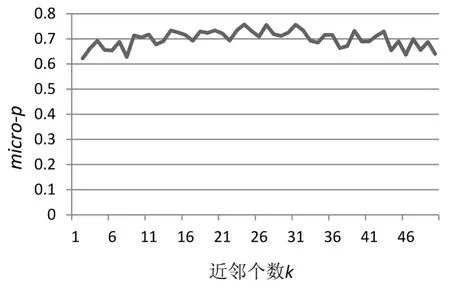
图3在ECG数据集上micro-p随近邻个数k变化情况

图4 在Gun Point数据集上micro-p随近邻个数k变化情况
4 总结
本文提出了基于局部线性嵌入的时间序列聚类方法,使用LLE方法对时间序列样本维数约简,在低维空间对维数约简后的数据进行聚类,通过将它的聚类性能与已有方法PCA、PAA进行比较,证明了这种方法更能提高聚类性能。在基于LLE的时间序列聚类中,有两个参数,一个是嵌入维数d,另一个是近邻个数k,如何选择“最优”的嵌入维数以及适当的近邻个数,值得今后进一步研究。
[1] 李海林.时间序列数据挖掘中的特征表示与相似性度量方法研究[D].大连:大连理工大学,2012.
[2] Jackson J E.A User's Guide to Principal Components[J].Series in Probability & Mathematical Statistics Applied Probability &Statistics,1991,29(1):493-494.
[3] Keogh E,Chakrabarti K ,Pazzani M,et al.Dimensionality reduction for fast similarity search in large time series databases[J].Journal of Knowledge and Information Systems,2000,3(3):263-286.
[4] Yi B K,Faloutsos C.Fast Time Sequence Indexing for Arbitrary Lp Norms[J].Vldb Journal,2000:385-394.
[5] Roweis ST,Saul LK.Nonlinear dimensionality reduction by Locally Linear Embedding[J].Science,2000,290:2323-2326.
[6] 翁小清,沈钧毅.多变量时间序列的异常识别与分类研究[D],西安,西安交通大学,2008.
[7] 李强,裘正定,孙冬梅,等.基于改进二维主成分分析的在线掌纹识别[J].电子学报,2005,33(10):1886-1889.
[8] Roweis ST,Saul LK.An Introduction to Locally Linear Embedding[J].Science,2000,290:2323-2326.
[9] Han JW,Kamber M.数据挖掘概念与技术[M].第3版,北京:机械工业出版社,2001.
[10] Zhou Z H,Tang W.Clusterer ensemble[J].Knowledge-Based Systems,2006,19(1):77-83.
[11] 唐伟,周志华.基于Bagging的选择性聚类集成[J].软件学报,2005,16(4):496-502.
[12] http://www.cs.ucr.edu/~eamonn/
[13] 盛骤,谢式千.概率论与数理统计[M].北京:高等教育出版社,2001.
