FAST工程馈源舱Stewart平台的机构精度标定
2015-05-08李建军王宇哲贾彦辉段艳宾
李建军,王宇哲,贾彦辉,段艳宾
(中国电子科技集团公司第五十四研究所,河北 石家庄 050080)
500m口径球面射电望远镜(简称FAST),是国家九大科技基础设施之一,采用我国科学家独创的设计和贵州独特喀斯特地貌,建设而成的高灵敏度、世界最大口径的巨型射电望远镜[1],如图1所示。
FAST望远镜工作在70MHz~3GHz频段,由8个馈源及1个16波束多波束馈源组成的接收机系统安装在馈源舱中。由于巨大的空间跨度,接收机与反射面之间难以建立高精度的刚性连接,FAST采用六根支撑索将馈源舱悬吊于空中,通过改变索的长度,拖动馈源舱在百米尺度工作空间内运动,并将馈源定位于瞬时焦点[2]。
馈源舱是馈源接收机的安装、保护及精调机构,集结构、机构、测量、控制等相关技术于一体,由星形框架、AB轴机构、Stewart平台等组成,直径Φ13m,重量约30t,如图2所示。

图1 500米口径球面射电望远镜
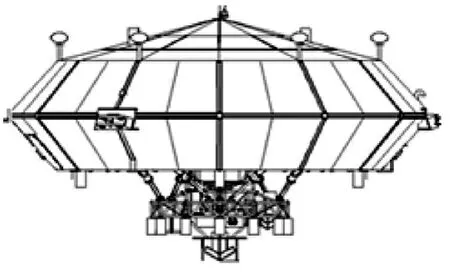
图2 馈源舱外形
Stewart平台是馈源舱核心部件,支撑在柔性悬挂平台之上,承载馈源及附属机构。由于结构刚度变形、风激引起的晃动、支撑索的振动耦合等外界因素,直接影响馈源的位姿精度,因此,Stewart平台的主要功能是克服外界扰动,通过大范围、高精度、高采样率的动态测量与控制技术,将馈源准确定位在毫米级的位置精度[3]。
1 Stewart平台的标定需求
Stewart平台由上平台、伸缩支腿、球铰、虎克铰等组成。上平台支撑在AB轴机构上,下平台安装馈源。Stewart平台外形尺寸φ4500×3000×2000mm,总重量5000kg,中心点的工作空间为半径150√2mm,高度300mm的圆柱体,如图3所示。
Stewart平台是并联机构中的经典构形,其关节运动副及六根运动杆件均为空间布置,属于复杂的空间多环路闭链机构。下平台的坐标位置和姿态与控制系统驱动坐标位置之间需要经过坐标变换,方可获得机构运动的数学描述,从而进行有效的控制,实现下平台的确定几何参数。由于巨大的空间尺度及30t的重量,使得杆件和铰链的制造及装配误差、上下平台的结构变形误差、测量误差、柔索扰动耦合等因素不可避免。而且这些误差对整机的影响非线性关系,导致Stewart平台的参数理论值和实际值将不可能一致,因此,需要测量下平台实际位姿,由并联机构学理论构造辨识方程,求解获得真实结构参数,利用误差数据进行补偿,确保机构定位精度满足预期要求。
Stewart平台标定内容包括:上平台虎克铰中心位姿误差参数18个,下平台球铰中心位姿误差参数18个,伸缩支腿原始长度误差参数6个,共计42个独立误差参数。
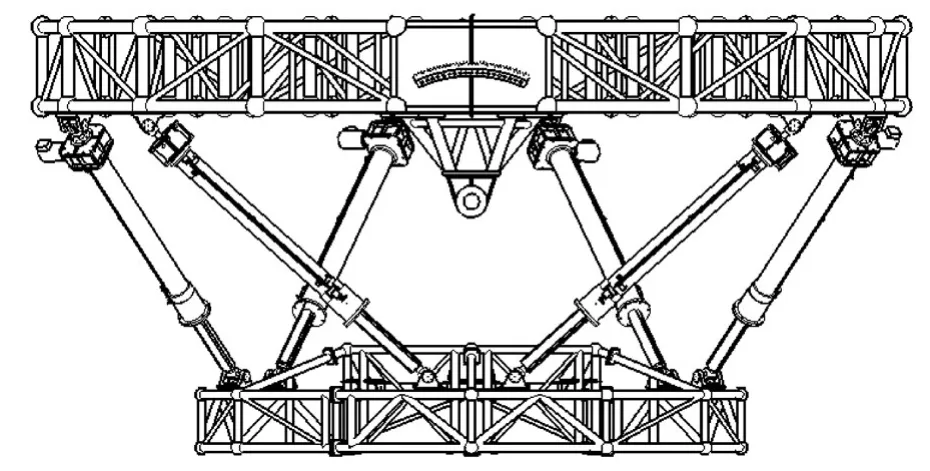
图3 Stewart平台
利用激光跟踪仪作为测量仪器,可同时测量Stewart平台的三个位置坐标和三个姿态转角信息。
2 Stewart平台的标定流程
Stewart平台的标定流程包括:建立工作坐标系、位姿测量规划、标定实施。
2.1 建立工作坐标系
Stewart平台的工作坐标系包括:测量坐标系、控制坐标系及标定坐标系,机构各参数在不同坐标系下的描述不同,因此,必须明确各坐标系的建立方式及变换关系,以实现测量数据基准与平台运动学参数基准的映射统一,确保机构标定有效。
首先确定激光跟踪仪的工作位置,建立测量基准坐标系。
在上、下平台上各三个合适位置安装靶镜,分别测量三个标志点坐标,确定平面并找出圆心,进而确定上、下平台坐标系以及坐标系原点在测量坐标系中的坐标。上、下平台坐标系三轴在测量坐标系中的描述可由转换矩阵表示,进而上、下平台坐标系之间的变换关系可以由此间接获得。
下平台坐标系原点在上平台坐标系中的位置描述为

下平台坐标系在上平台坐标系中的姿态可描述为

2.2 位姿测量规划
待标定的机构学误差参数为42个,为了描述误差各分布和变化,根据Stewart平台工作空间,首先进行位姿规划,如表1所示。
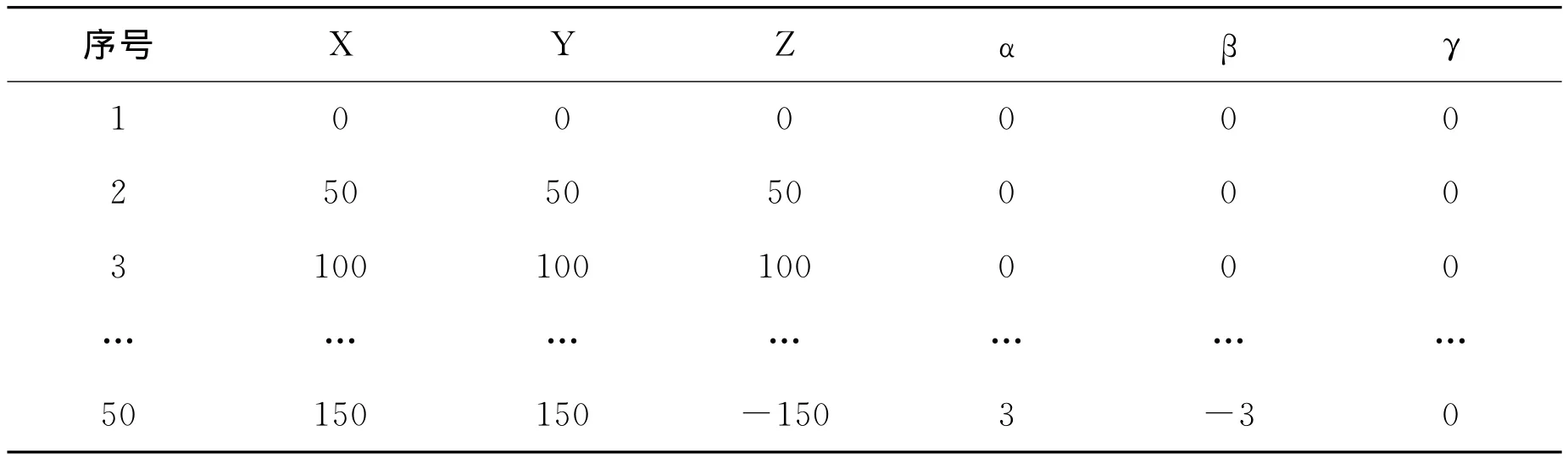
表1 规划位姿
机构按照给定的位姿运动,测量各位姿下的6个姿态参数(xyzαβγ)。在测量过程中,测量坐标系与上平台坐标系不变,控制机构使下平台按照规划位姿变化,由激光跟踪仪测量下平台位姿,根据坐标系变化关系可得其在上平台坐标系中的表示。
2.3 标定实施步骤
结合Stewart平台工作范围,对42个机构学参数进行全标定。首先将Stewart平台整体倾斜40°,依据前述流程,获得42个机构学误差参数;以此为基准,评判其是否满足倾斜角为30°时精度;若满足,进而评判倾斜角分别为20°、10°、0°时的机构运动情况;若不满足,则针对倾斜角为30°时进行标定,再次获得一组机构学误差参数。循环前述过程,以在各节点机构定位精度均满足预期要求为目标逐段进行标定,获得多组机构学误差参数。每组参数可保证某一范围内机构的定位精度,全部参数可涵盖Stewart平台整个工作范围。即对应每一个姿态,均有相应的参数保证机构运动精度符合目标要求。
由并联机构学理论,运动学反解公式

式中,li(i=1,2,…,6)为各驱动腿的杆长,BPAi为与下平台球铰在上平台坐标系{B}中的坐标表示,BPBi=[xBiyBizBi]T为与上平台虎克铰在上平台坐标系{B}中的坐标表示,BAT为从下平台坐标系{A}到上平台坐标系{B}的变换矩阵,APAi=[xAiyAizAi]T为与球铰在下平台坐标系{A}中的坐标表示。
下平台每变换一种位姿,针对每个分支即可由式(3)构造一个约束方程,每个分支有7个参数,6个分支共有42个待标定参数。故下平台只需变换7个姿态即能构造出42个约束方程以实现机构全部分支的运动学标定。
将误差补偿参数以数据库形式提供给控制系统,控制系统根据不同的工况调取不同的标定参数进行控制。具体的位姿测量实施步骤如图4所示。

图4 标定实施步骤
3 结论
本文基于FAST工程的项目特点,以及及馈源接收机的位姿精度需求,通过分析馈源舱系统Stewart平台的结构组成、机构原理及误差来源,结合Stewart平台的运行环境,提出了Stewart平台的标定方案,通过机构前期的精度标定,将误差补偿参数以数据库形式提供给控制系统,以满足FAST工程的科学需求。
[1] 黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.
[2] 刘大炜,王立平,李铁民,等.一类带冗余支链并联机构的运动学自标定[J].机械工程学报,2012,481(1):1-6.
[3] 成大先.机械设计手册[M].北京:化学工业出版社,2002.
