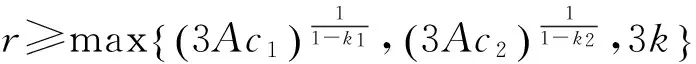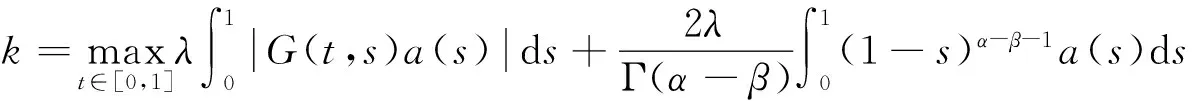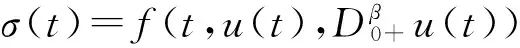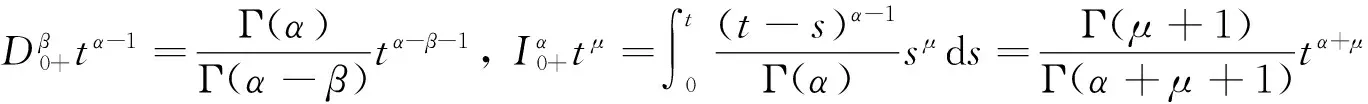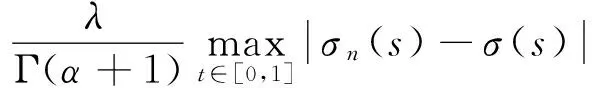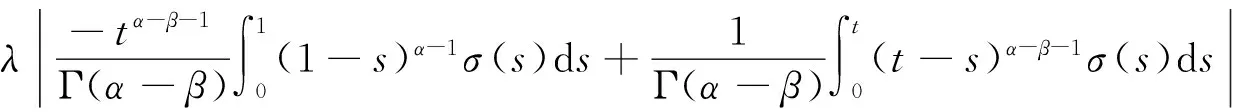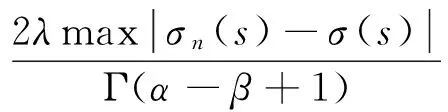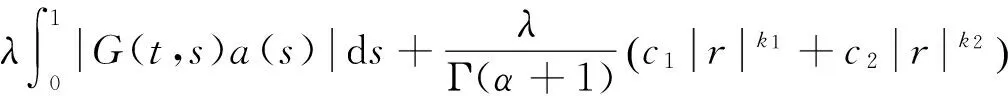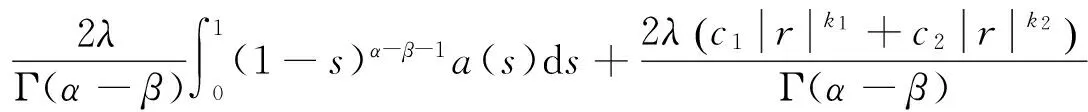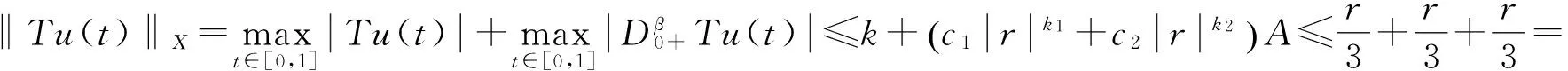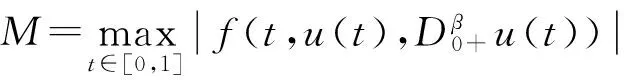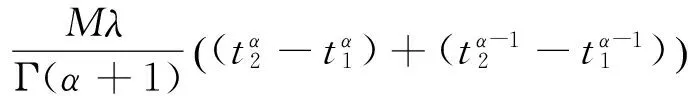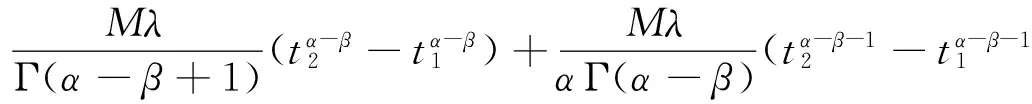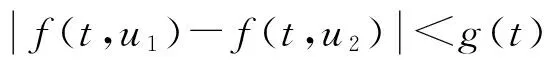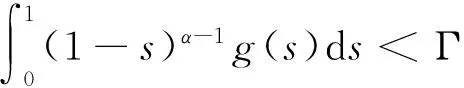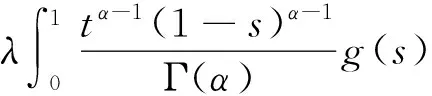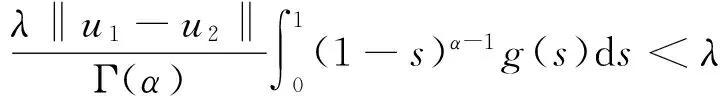非线性分数阶微分方程边值问题解的存在性和唯一性

张爱华，胡卫敏

(1.伊犁师范学院数学与统计学院，新疆 伊宁 835000；2.菏泽市第二中学，山东 菏泽 274000)

非线性分数阶微分方程边值问题解的存在性和唯一性

张爱华1，2，胡卫敏1

(1.伊犁师范学院数学与统计学院，新疆 伊宁 835000；2.菏泽市第二中学，山东 菏泽 274000)

主要研究了非线性分数阶微分方程边值问题

分数阶微分方程；边值问题；分数阶格林函数；不动点定理

0 引言

近年来，分数阶微分方程已经成为国内外的一个研究热点，受到人们越来越多的关注.分数阶微分方程不仅具有丰富的理论内涵，还在流体力学、材料力学、等离子体物理学、多孔介质的动力学、黏弹性、大气海洋运动学、生物学、金融学等方面有着广泛地应用[1-3].

目前，一些学者应用非线性分析的技巧研究非线性分数阶微分方程边值问题正解的存在性和多重性.文献[4]研究了非线性分数阶微分方程边值问题

文献[5]讨论了非线性分数阶微分方程边值问题

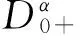
本文讨论了非线性分数阶微分方程边值问题

(1)

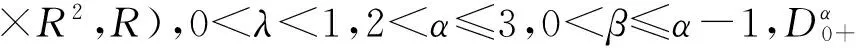
1 预备知识

定义1.1[6]函数y:(0，∞)→R的α>0阶Riemann-Liouville分数阶积分是指

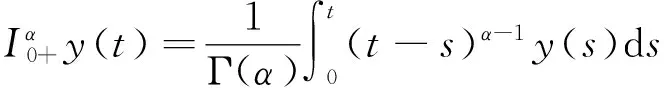
其中右边是在(0，∞)上逐点定义的.

定义1.2[7]函数y:(0，∞)→R的α>0阶Riemann-Liouville分数阶微分是指

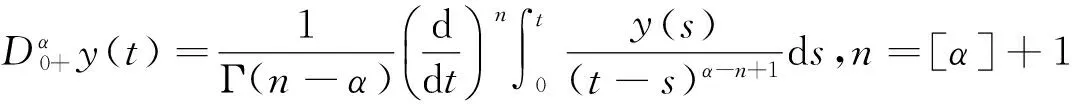
其中右边是在(0，∞)上逐点定义的.

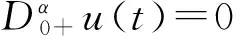
u(t)=C1tα-1+C2tα-2+…+CNtα-N，

其中Ci∈R为常数，i=1，2，…，N，N是大于或等于α的最小整数.

引理1.2[8]假设u∈C(0，1)∩L(0，1)，且有α>0阶分数阶导数，则

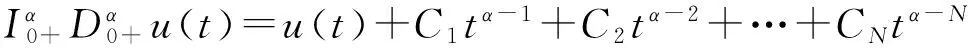
其中Ci∈R为常数，i=1，2，…，N，N是大于或等于α的最小整数.

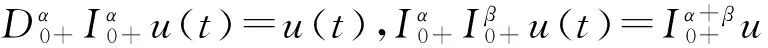
引理1.4 给定y∈C[0，1]，2<α≤3，则方程

(2)

(3)

这里G(t，s)称作边值问题(2)的格林函数.

证明 由引理1.2和定义1.1，分数阶微分方程(2)等价于积分方程

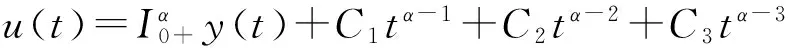
其中C1，C2，C3∈R.因此方程(2)的解为

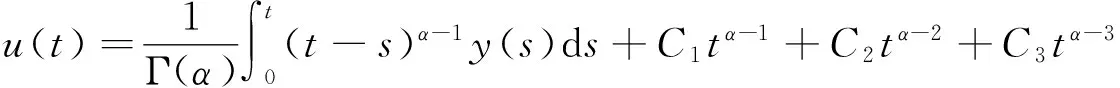
从而

(α-1)C1tα-2+(α-2)C2tα-3+(α-3)C3tα-4.

由u(0)=u′(0)=0知C2=C3=0，又u(1)=0，所以

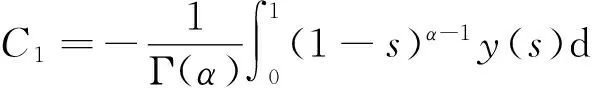
综上，方程(2)的唯一解为

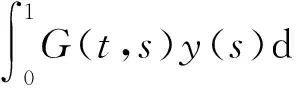
引理1.5 ∀t，s∈(0，1)，(3)式定义的函数G(t，s)具有下列性质：

(ⅰ)G(t，s)<0;

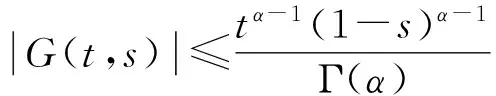
证明 (ⅰ) 当0≤t≤s≤1时，显然G(t，s)<0；当0≤s≤t≤1时，

(t-s)α-1-tα-1(1-s)α-1=(t-s)α-1-(t-ts)α-1<0，

由(3)式显然G(t，s)<0，结论成立.

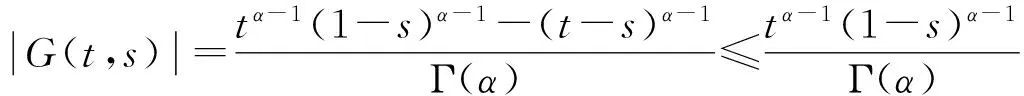
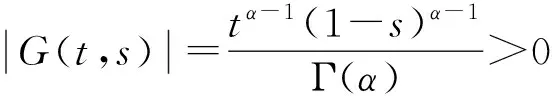
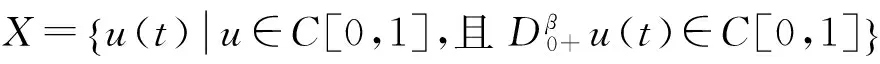
定义算子T:X→X，

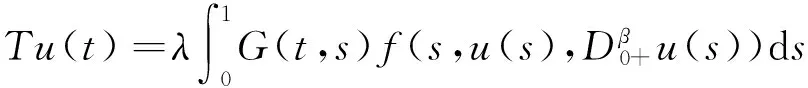
则分数阶边值问题(1)有解等价于算子方程Tu=u有不动点.

2 主要结果

定理2.1 假设f∈C([0，1]×R2，R)，且存在一个非负函数a(t)∈L[0，1]，使得

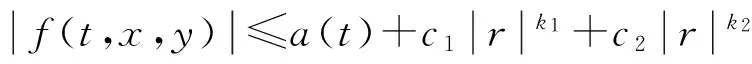
其中c1，c2≥0，0

证明 记

其中

∀u(t)∈U，μ>-1，由引理1.2，注意到

先证T是连续算子.事实上，若u∈U，un∈U，n=0，1，2，…，并且当n→∞时，有‖un-u‖→0.由f的连续性，当t∈[0，1]时，

因此T是连续算子.又因为

(4)

所以

下面证明T:U→U.

由(4)式得

又有

因为tα-1，tα，tα-β，tα-β-1在[0，1]上都一致连续，所以TU是等度连续的.又TU⊂U，故一致有界，因此T是全连续算子.由Schauder不动点定理可知，分数阶微分方程边值问题(1)在U中至少有一个解.

定理2.2 假设f∈C([0，1]×R2，R)，且∀t∈[0，1]，u1，u2∈X，有g(t)>0，使得函数f(t，u)满足：

则边值问题(1)存在唯一解.

证明 由格林函数G(t，s)的定义及f的连续性，∀u1，u2∈X，t∈[0，1]，有

由于0<λ<1，故算子T是压缩的.由Banach压缩映像原理可知，边值问题(1)存在唯一解.

[1] KILBAS A A，SRIVASTAVA H M，TRUJILLO J J. Theory and applications of fractional differential equations[M]. Amsterda：Elsevier Science B V，2006:56-90.

[2] RAHIMY M. Applications of fractional differential equations[J]. Applied Mathematical Sciences，2010，4(50)：2453-2461.

[3] NONNENMACHER T F，METZLER R. On the Riemann-Liouville fractional calculus and some recent applications[J]. Fractals，1995，3(3)：557-566.

[4] XIONG Y，ZHONG L W，WEI D. Existence of positive solutions for the boundary value problem of nonlinear fractional differential equations [J]. Commun Nonlinear Sci Numer Simulat，2012，17：85-92.

[5] 王刚.分数阶微分方程边值问题解的存在性[J].中国科技论文在线，2010，9:1-4.

[6] 张稳根，胡卫敏，刘刚. 非线性分数阶微分方程组奇异对偶系统正解的存在性证明[J]. 东北师大学报(自然科学版)，2015，47(2):14-20.

[7] 张爱华，胡卫敏.一类分数阶脉冲微分方程边值问题的多重正解[J]. 东北师大学报(自然科学版)，2015，47(3):12-18.

[8] BAI Z B，LÜ H S. Positive solutions for boundary value problem of nonlinear fractional differential equation [J].Math Anal Appl，2005，311：495-505.

[9] ZHANG S Q. Positive solutions for boundary-value problems of nonlinear fractional differential equations [J]. Electronic Journal of Differential Equations，2006，36：1-12.

(责任编辑：李亚军)

Existence and uniqueness of solutions for boundary value problem of nonlinear fractional differential equation

ZHANG Ai-hua1，2，HU Wei-min1

(1.School of Mathematics and Statistics，Yili Normal University，Yining 835000，China；2.The Second High Middle School of Heze City，Heze 274000，China)

The existence and uniqueness of positive solutions for a nonlinear fractional differential equation boundary-value problem are considered：whereandarethestandardRiemann-Liouvilledifferentiation.SomeexistenceresultsofsolutionsareobtainedbymeansofSchauderfixed-pointtheorem.Then，theuniquenessofsolutionisobtainedbyusingBanachcontractionmapprinciple.

fractionaldifferentialequation；boundary-valueproblem；fractionalGreen’sfunction；fixed-pointtheorem

1000-1832(2015)04-0036-06

10.16163/j.cnki.22-1123/n.2015.04.008

2014-03-18

新疆维吾尔自治区自然科学基金资助项目(201318101-14).

张爱华(1984—)，女，硕士，主要从事分数阶微分方程边值问题研究；通讯作者：胡卫敏(1968—)，男，教授，主要从事微分方程理论与应用研究.

O

A