例谈研究高考试题的若干切入点

☉武汉市黄陂区第一中学盘龙校区李红春

例谈研究高考试题的若干切入点

☉武汉市黄陂区第一中学盘龙校区李红春

高考是我国现行的一种最为重要的选拔性考试，其重要性是不言而喻，高考试题设计新颖，构思巧妙，集中体现了命题专家的智慧，是我们学习的典范，研究高考试题，探求命题者的立意、试题的解法、试题的背景、结论的拓展、试题的导向、试题的评价等对提升高三复习备考的针对性有着重要的意义·本文通过对2014年高考广东卷理科第20题的研究，谈谈研究高考试题的若干切入点·

（1）求椭圆C的标准方程；

（2）若动点P（x0、y0）为椭圆外一点，且点P到椭圆C的两条切线相互垂直，求点P的轨迹方程·

一、研究试题的考查目标

研究试题的考查目的就是研究试题的立意，高考试题通常在知识的交汇处命题，以基础知识、基本技能、和基本数学思想方法为载体，着力考查学生的能力·本题以椭圆为载体进行构思，将直线与椭圆的位置关系、直线与直线的位置关系等条件有机地呈现给学生，要求动点的轨迹问题，旨在考查学生对“数形结合、分类讨论、转化与化归”等思想的运用，以及观察、分析、类比、推理运算等能力·

二、研究试题解法的关键节点

掌握数学就意味着解题，一道试题难，并不是每一步都难，一种解法妙，往往有其意料之外的东西，一道难题总有些步骤是解题的关键节点，作为教师就要认真分析其中的奥秘，知其然还要知其所以然，教师只有深刻领悟课堂教学中才能提纲挈领，有的放矢·

（2）设两切线为l1，l2·

①当l1⊥x轴或l1∥x轴时，对应l2∥x轴或轴l2⊥x轴，可知P（±3，±2）·x2+18（y0-kx0）kx+9（y0-kx0）2-36=0·

若直线与椭圆相切，则Δ=0，即9（y0-kx0）2k2-（9k2+4）·

②当直线l1与l2的斜率均存在且都不为零时，设过点

因直线l1，l2均与椭圆相切，故其斜率k1，k2恰是方程点P的轨迹方程为x2+y2=13（x≠±3），且P（±3，±2）满足上式·

综上知：点P的轨迹方程为x2+y2=13·

以上解答过程中，两直线的斜率k1，k2我们称之为等价元素，由于地位完全相同，它们所满足的等量关系也是相同的，由两个结构相同的等量关系抽象出一个方程，而k1、k2就是方程的解，体现了解析几何中设而不求的思想·这种依据“等价元素与方程思想”的解题策略是以上解法的最大亮点和关键节点，在后继的教学中教师就应该把这种解题思想渗透到日常的解题教学中·

三、研究试题的命制背景

作为数学的学习与研究，如果仅仅停留在把题目答案找出来，其实远远不够，为解题而解题，学生的数学思维能力和认知很难得到有效提高，在数学解题过程中我们要学会透过现象，看清命题的本源·本题中点P的轨迹就是初等数学里著名的蒙日圆，在椭圆中，任意两条互相垂直的切线的交点都在同一个圆上，它的圆心是椭圆中心，半径等于长短轴平方和的算数平方根，这个圆叫蒙日圆·关于蒙日圆，有如下优美性质：

证明：设点P（x0，y0），过点P的直线方程为y-y0=k（xx0），代入椭圆方程得（a2k2+b2）x2+2ka（2y0-kx0）·x+a（2y0-kx0）2-a2b2=0·若直线与椭圆相切，则Δ=［2ka（2y0-kx0）］2-4（a2k2+b2）［a（2y0-kx0）2-a2b2］=0，即（a2-k2+2x0y0k+b2-= 0，若两条直线m、n的斜率均存在且都不为零，不妨设它们分别为k1、k2，如图1，因两条直线均与椭圆相切，故其斜率k1、k2恰是轴，可知P（±a，±b）也满足方程，故P点的轨迹为圆x2+y2= a2+b2·

从初等数学研究的成果中选取的素材，以此为基础将其变抽象为具体，通过搭桥与构题，加工与调整形成的试题，这是常见的一种命题途径·在教学过程中，通过挖掘试题命制过程中依据的性质背景，有助于透过现象看清本质，缩短思维流程，从而达到举一反三，跳出题海，进行有效教学的目的·

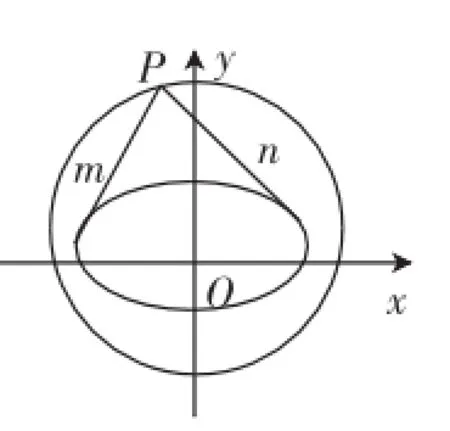
图1

四、研究相关试题的联系

任何数学问题的出现都有一定的情境，数学问题不会无端地“迸发”出来，往届高考和调考试题一直是新高考试题的重要来源，命题专家一直重视传承和相互借鉴，作为教师要努力从历年高考题的整体研究中找到共性，从近几年高考题中找到高考的变化趋势，从对同类试题的研究中找到变化，不断提升复习效率·

（1）求椭圆C的方程和其“准圆”方程·

（2）点P是椭圆C的“准圆”上的一个动点，过动点P作直线l1、l2，使得l1、l2与椭圆C都只有一个交点，且l1、l2分别交其“准圆”于点M、N，求证：为|MN|定值·

例3（2012年高考湖南卷）在直角坐标系xOy中，曲线C1上的点均在圆C2：（x-5）2+y2=9外，且对C1上任意一点M，M到直线x=-2的距离等于该点与圆C2上点的距离的最小值·

（1）求曲线C1的方程；

（2）设P（x0，y0）（y0≠3）为圆C2外一点，过点P作圆C2的两条切线，分别与曲线C1相交于点A，B和C，D·证明：当点P在直线x=-4上运动时，四点A、B、C、D的纵坐标之积为定值·

例2和例1都以蒙日圆为背景，例3和例1解决问题的核心方法一样，都是用“等价元素与方程思想”解题·

五、研究试题的结论拓展

将试题进行拓展研究，是实施研究性学习的一个重要举措，研究性学习的目的在于“改变学生以单纯地接受教师传授知识为主的学习方式，为学生构建开放的学习环境，提供多渠道获取知识并将学到的知识加以综合应用于实践的机会，培养创新精神和实践能力”，将试题进行拓展，常见的方式有：横向类比、逆向思考、特殊到一般的抽象、一般到特殊的发现等·将本题进行拓展我们可以得到如下一些结论：

六、研究试题的价值导向

高考试题是复习备考的风向标，它的指挥棒功能毋容置疑，从某种意义上来说，高考试题的导向功能胜过其编制的精巧和深奥·本题紧扣《考试说明》，密切结合教材，沿袭了“在丰富背景下立意，在贴近教材中设计”的命题风格，不随意拔高考点，不刻意追求别致，紧贴课本·课改的不断推进对高考命题也提出了更高的要求，要求试题在创新的同时更能全面考查学生的数学素养，本题作为圆锥曲线试题，在继承传统圆锥曲线问题解决方法的同时要求考生善于观察、类比，能借助“等价元素与方程”的思想辅助解题，这样的方法不落俗套，这就要求一线教师要摆脱死教书的习惯，少做点机械的训练，多做点深入的研究，积极倡导自主、合作、探究的新型学习方式，在课堂教学中注重知识的发生过程，善于捕捉探究资源，激发学生的思维热情，引导学生探究知识，不断提升学生的探究能力，这既是高考试题的检测方向，更是教学中要重点解决的问题·

七、研究考后试题的社会评价

一道好的试题必须考虑到“难度、信度、效度、区分度”四个方面，命题也是一项充满遗憾的艺术，考试结果和社会评价在一定程度上左右着后继者在命题中的一些做法，是坚持还是放弃，是批判还是继承，作为教师关注舆情十分重要·

最后，笔者要强调的是：研究高考试题是教师的一项基本功，从某种程度上说，选好“研究内容”比“选择研究方法”更重要，因为内容确立的是目标，决定了我们研究的“方向”，而研究方法确定的是解决问题的“方式”，“方式服从于方向”，建议老师们今后多选择一些“立意鲜明、解法多样、背景深刻、推广自然、评价良好”的试题作为研究对象·

1·赵思林·研究高考试题的几种视角［J］·中学数学教学参考（上），2009（4）·

2·李红春·从一道试题的求解管窥研究性学习的几个视角［J］·教学月刊（中学版），2014（11）·

2·李红春·一道高考题的背景及拓展［J］·高中数学教与学，2014（12）·F