结合FFT和Gabor滤波器的织物纹理特征提取方法

任 静, 周 华, 郭 超, 王 妍, 梅再欢

(浙江理工大学先进纺织材料与制备技术教育部重点实验室, 杭州 310018)

结合FFT和Gabor滤波器的织物纹理特征提取方法

任 静, 周 华, 郭 超, 王 妍, 梅再欢

(浙江理工大学先进纺织材料与制备技术教育部重点实验室, 杭州 310018)

针对织物表面纹理特征提取与表征的问题,提出一种结合FFT(傅里叶变换)和Gabor滤波器的织物纹理特征提取方法,通过傅里叶变换提取频谱楔特征(角向分布)和环特征(径向分布)作为特征角度和频率参数,设计2个最优Gabor滤波器,分别与织物纹理图像进行卷积,获得目标子图像,然后对子图像进行融合处理,达到提取纹理特征的目的。在线条图像纹理特征成功提取的前提下,应用到常见织物的纹理特征提取上,并与传统的Gabor滤波器提取方法进行对比。实验结果表明,结合FFT和Gabor滤波器的织物纹理特征提取方法是有效的,且提取结果优于传统方法。

傅里叶变换; Gabor滤波器; 织物纹理; 特征提取

0 引 言

纹理概念源于人体肌肤对物体表面光滑、粗糙等触感的反馈[1],在此基础上结合人类视觉机理,演变成为描述物体表面物理属性的视觉信息,用以衡量规则度、密度、光滑度、细致度、线性度、颗粒度、均一性、方向性等固有属性。织物的纹理是织物的一种风格特征,不同的纹理在视觉和触觉上都会形成不同的感受。它反映了织物的表观结构,是织物外观视觉的重要属性之一,直接影响到人对织物颜色的主观感觉。在计算机视觉研究中,纹理特征的本质是研究图像相邻像素点灰度的空间分布情况。研究者们通过结合时频分析、分形学、神经网络等数学方法,使得纹理特征的提取由单一尺度和方向发展到多尺度和多方向;纹理特征的提取方法也由单一的统计分析法演变发展到数种有价值的方法。目前图像纹理的表征方法主要有四大类:统计分析法[2-3]、结构分析法[4]、模型法和频域法。采用多通道滤波器提取图像的纹理特征是频域法中最典型的方式。其中,Gabor滤波器在各行各领域的应用最为广泛,在织物疵点检测,织物纹理分割、分类、识别领域更是发挥了不小的作用[5-10]。采用Gabor滤波器提取纹理特征的传统方法是选定典型的8个方向、5个频率,设计一组由40个不同滤波器组成的滤波器组,每个滤波器用于抽取特定方向和频率的纹理信息,以图像滤波系数为特征形成的特征向量维数高、针对性低、重点不突出而且多个滤波器的计算量大、处理速度慢。

傅里叶变换是一种经典谱变换,基本思想是将信号从时域转换到频域,实质是将任意函数分解为无限多个不同频率的正弦或者余弦信号和的形式。本文提出一种结合FFT和Gabor滤波器的织物纹理特征提取方法。该方法以织物纹理图像通过傅里叶变换提取的楔特征(角向分布)和环特征(径向分布)作为纹理特征角度和频率,在此基础上设计2个最优的Gabor滤波器,对织物纹理图像进行过滤,可大大减少滤波器的个数,降低计算量,也使得特征的提取更具针对性。

1 Gabor滤波器

二维Gabor函数的定义为:

g(x,y)=

(1)

其中σx和σy控制高斯函数在x轴和y轴的伸缩程度,如果σx=σy,高斯截面为圆对称,否则为椭圆;作为Gabor带通滤波器的径向中心频率,决定了滤波器在频域中的位置。由于高斯函数的局部性特征,致使Gabor滤波器只在局部起作用。同时,因为被调制的正弦波只针对x坐标,即Gabor滤波器是在x轴方向被高斯函数调制的正弦波,实际上在y方向上相当于被调制的是一个直流分量。由此可见,Gabor滤波器是一个在x方向上带通,在y方向上低通的滤波器。[11]

二维Gabor函数的傅立叶变换为:

(2)

以g(x,y)为母小波,通过对g(x,y)进行适当尺度变换和旋转变换,可以得到自相似的一组滤波器,称为Gabor小波函数:

gmn(x,y)=a-mg(x′,y′),a>1,m,n∈Z

(3)

其中:x′=a-mg(xcosθ+ysinθ),y′=a-m(-xsinθ+ycosθ),θ=nπ/K,K表示总的方向数目(n∈[0,K]),a-m为尺度因子。由傅里叶变换的性特性可知,u′=ucosθ+vsinθ,v′=-usinθ+vcosθ通过改变m和n的值,可以得到一组方向和尺度不同的滤波器。

2 结合FFT和Gabor滤波器的纹理特征提取方法

Gabor滤波器具有时域和频域的联合最佳分辨率,并且较好地模拟了人类视觉系统的视觉感受特性。其主要思想是:不同纹理一般具有不同的中心频率和方向特性,根据这一特性可以设计一组Gabor滤波器组对图像进行滤波,每个Gabor滤波器只允许相对应的纹理顺利通过,而使其他纹理的能量受到抑制。这种多通道Gabor滤波器的方法旨在实现频域内最优覆盖,每个滤波器用于抽取特定方向和频率的纹理信息,但这种方法针对性低、重点不突出而且多个滤波器的计算量大、处理速度慢。如果能寻找到一组最优的Gabor滤波器与特征纹理相匹配,那么不仅减少了滤波器的个数,提高运算速度,而且可优化纹理特征的提取。因此,本文提出一种结合FFT和Gabor滤波器的纹理特征提取方法,设计思路和原理如下:

a) 滤波器角度参数θ的确定。二维图像的频谱图分析一般采用辐射状扫描法,即以频谱的中心为原点,以同心圆环或扇面的形式向四周作辐射状扫描,求出一定环形区域或一定扇面区域内各次谐波能量的总和,分别得到其环特征(径向分布)和楔特征(角向分布)。楔特征常用来分析纹理的方向性。织物纹理一般具有较为明显的方向性,本文通过对频谱图进行角向分布采样,得到角度-频谱曲线(角向分布),根据其峰值位置确定纹理特征的方向性。

b) 滤波器中心频率f的确定。分别沿滤波器方向进行径向分布分析,形成频谱沿滤波器方向的环特征,即频率-频谱曲线。频谱环特征(径向分布)常用来分析纹理的粗细程度和周期性强弱,而织物纹理图像一般具有明显的周期性。因此,频率-频谱曲线(径向分布)必然存在比较明显的波峰,代表着滤波器的中心频率。

c) 滤波器的标准差σx、σy的确定。σx、σy共同决定了滤波器的带宽,取值过大时,不利于表示图像的局部特性;若取值小,则容易受到噪声的干扰。基于生理视觉的研究表明,σy/σx的取值区间为0.23～0.92,本文取值为0.5。

根据这一设计思路,本文为每块织物设计订制了2个最优滤波器,先以线条纹理图像为例,进行特征提取,具体的实现步骤如下:

a) 获取大小为M×N(本文取256×256)的纹理图像I(x,y),进行快速傅立叶变换,得到相应的频谱图F(u,v)。

(4)

其中,M、N分别表示图像的宽度和高度,(x,y)表示图像的空间坐标,(u,v)表示空间频率分量。

b) 纹理特征提取:将频谱图像转化到极坐标下,采用辐射状扫描法得到角度-频谱曲线(角向分布)和频率-频谱曲线(径向分布)。

(5)

S(r)=Sθ(r)

(6)

其中,R0是以原点为中心的圆的半径,S(θ)表示旋转角度为θ时所有频谱图像像素值的总和,S(r)表示沿θ方向离圆心距离为r的频谱图像像素值之和。

c) 设计2个滤波器g1(σx,σy,f1,θ1),g2(σx,σy,f2,θ2),其中,σx=1,σy=0.5;中心频率f取频率-频谱曲线的明显特征峰值;角度θ取角度-频谱曲线的明显特征峰值。

d) 将原图像I分别和每个Gabor滤波器的实部和虚部卷积,得到特定频率和角度下的目标子图像I′(x,y):

I′(x,y)={[real(g(x,y))*I(x,y)]2+ [imag(g(x,y))*I(x,y)]2}1/2

(7)

e) 融合滤波后的目标子图像,即叠加提取的特定纹理特征,得到融合图像,融合后的图像含有原图像的主要纹理特征,是其特有的属性:

(8)

f) 计算纹理特征能量值,即滤波后融合图像的像素之和占原图像的像素之和的比例:

(9)

E(x,y)代表提取的特征纹理占原图像的比例,即原图像中含有该特征的纹理有多少。提取的特征纹理是原图像所特有的属性,能量值将该属性量化,可以准确地度量原图像的特征纹理。

3 实验结果

采用本文给出的纹理特征提取方法,对大小为256×256的线条纹理图像进行纹理特征提取和表征。图1为原图像,图2为傅里叶变换后的频谱图。

图1 纹理图像I

图2频谱图中的亮点呈中心对称分布,每一个亮点都代表不同的频率成分,而且亮点的大小和位置反映了不同成分的周期和取向。图3为角度-频谱曲线图,可以看出,纹理图像I在多个方向上都有较强的能量分布,其中,在θ1=43°和θ2=156°上存在大量纹理特征信息。图4和图5分别为沿θ1和θ2方向的频率-频谱曲线,图4中在r=4有强峰值,图5中在r=9有强峰值,说明纹理图像I在这两个频率上具有明显的周期性。

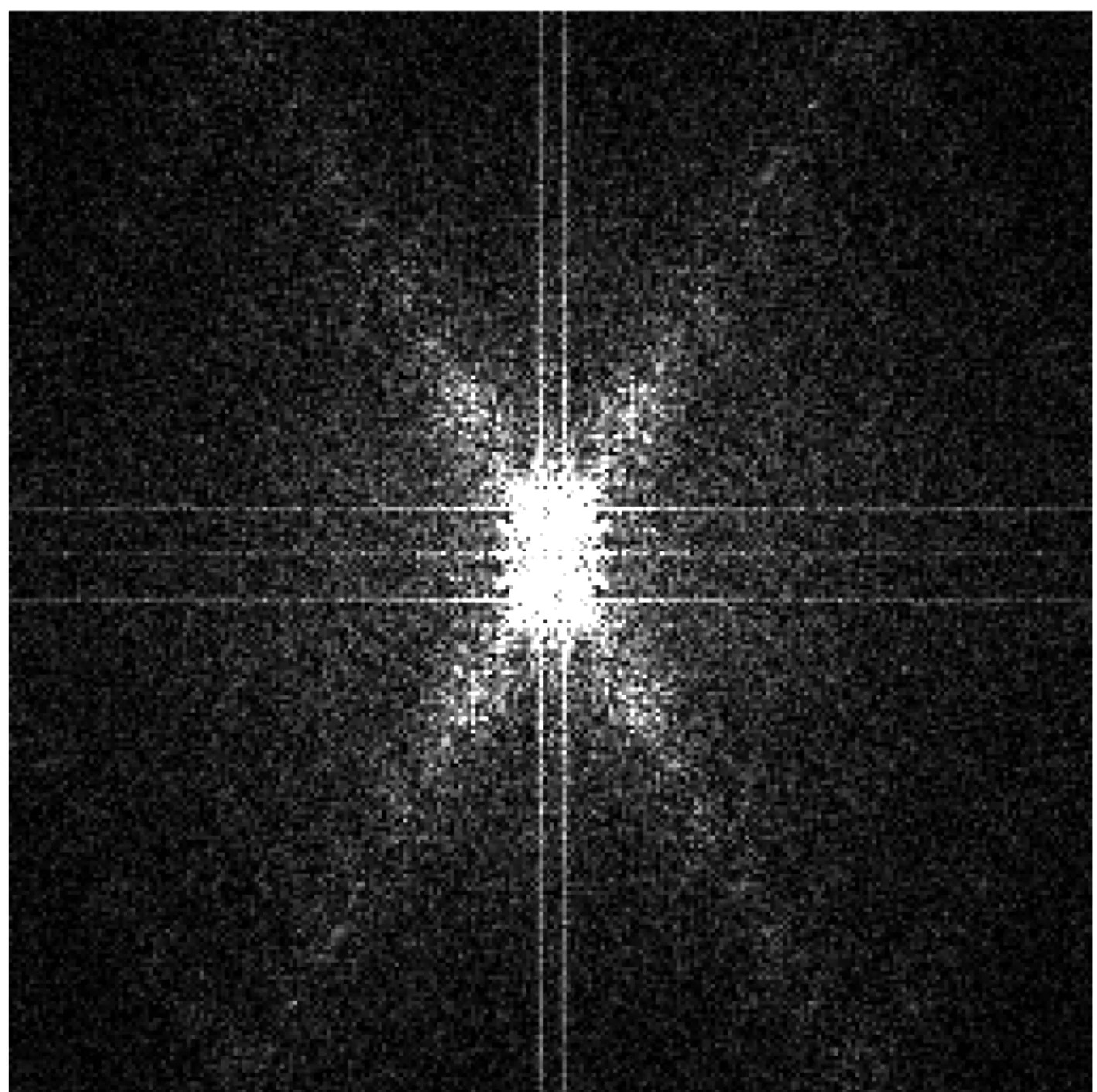
图2 频谱图F

图3 角度-频谱曲线

图4 θ1方向频率-频谱曲线

图5 θ2方向频率-频谱曲线

取角度-频谱曲线的最大峰值θ1=43°和θ2=156°作为角度参数,取θ1方向频率-频谱曲线的最大峰值频率f1(4/128),θ2方向频率-频谱曲线的最大峰值频率作为滤波器的频率参数f2(9/128),代入Gabor滤波器频域表达式,构成2个最优滤波器。将原图像分别和2个滤波器的实部和虚部卷积,得到2幅目标子图像的融合结果，如图6所示。滤波后的融合图像,提取了原图像的主要纹理特征。通过对比图1和图6发现,结合FFT和Gabor滤波器的纹理特征提取方法对图像的纹理特征提取效果令人满意。

图6 滤波后的融合图像

在验证了该方法的有效性后,用本文提出的方法对大小为256×256的四种不同织物纹理图像进行纹理特征提取和表征,并与传统的方法进行比较,提取结果如图7-图10所示。

从提取结果来看,本文提出的方法明显优于传统方法。尤其是对于组织点相对较小和组织结构相对复杂的织物,传统方法的提取结果很不理想,而本文方法能够很好地提取其纹理特征。表1为织物的纹理特征参数,4块织物都有其特有的特征角度和特征频率。织物原图像与以特征角度和特征频率为参数设计的最优滤波器卷积后,得到的过滤图像与织物原图像的像素和之比是织物的特征纹理能量值E,4块织物也有特有的纹理能量值E。E1是4块织物都用织物1的最优滤波器过滤,通过计算过滤图像与织物原图像的像素和之比得到的特征纹理能量值。同理,E2、E3和E4均分别用织物2、3、4的最优滤波器过滤所得到的特征纹理能量值。对于织物1来说,E1是通过自身的最优滤波器过滤的图像与织物1原图像的像素和之比得到的特征纹理能量值,即E=E1。这种纹理是织物1最明显的特征纹理,故均大于E2、E3和E4。其它3块织物的纹理能量值也存在着相同的规律。

图7 织物1

图8 织物2

图9 织物3

图10 织物4

织物特征角度θ1/(°)特征频率f1(1/128Hz)特征角度θ2/(°)特征频率f2(1/128Hz)纹理能量值E纹理能量E1纹理能量E2纹理能量E3纹理能量E4织物11123943170．31920．31920．09230．27330．1578织物218025169280．29960．14740．29960．25140．1476织物36217175190．30660．13880．09440．30660．1367织物417519180600．20320．12020．09170．17490．2032

4 结 论

以织物纹理作为研究对象,提出一种结合FFT和Gabor滤波器的织物纹理特征提取方法。通过对织物纹理图像进行傅里叶变换,提取频谱的楔特征(角向分布)确定了Gabor滤波器的方向参数,将传统的8个方向滤波器减少至2个,改善了特征的针对性,降低了计算量。并沿着滤波器方向对频谱进行环特征(径向分布)分析,获取Gabor滤波器的中心频率,增强了纹理特征描述的有效性。以纹理的2个特征方向和相应的中心频率设计了2个滤波器,将传统的40个滤波器组减至2个最优的滤波器,解决了滤波器组计算量过大的瓶颈问题,同时增强了特征的聚焦分析能力。实验结果表明,织物纹理特征提取效果良好,且优于传统方法的提取结果。

[1] Janet J, Payne S, Stonham T J. Can texture and image content retrieval methods match human perception[C]//Proceeding of Intemational Symposium on Intelligent Multimedia, Video and Speech Processing, 2001: 154-157.

[2] Varma M, Zisserman A. Unifying statistical texture classification frameworks.[J] Image and Vision Computing, 2004, 22: 1175-1183.

[3] 苑丽红, 付 丽, 杨 勇, 等. 灰度共生矩阵提取纹理特征的实验结果分析[J]. 计算机应用, 2009, 29(4): 1018-1021.

[4] 王惠明. 图像纹理特征的提取方法[J]. 中国传媒大学学报: 自然科学版, 2006, 13(1): 4-8.

[5] 尹 芳, 陈德运, 吴 锐. 改进的Gabor小波变换特征提取方法[J]. 计算机工程, 2012, 38(15): 145-147.

[6] 陈树越, 冯 军. 基于尺度变换的Gabor滤波器织物疵点检测[J]. 纺织学报, 2010, 31(9): 38-41.

[7] Bodnarova A, Bennamoun M, Latham S. Optimal Gabor filters for textile flaw detection[J]. Pattern Recognition, 2002, 35(12): 2973.

[8] Mak K, Peng P. An automated inspection system for textile fabrics based on Gabor filters[J]. Robotics & Computer-Integrated Manufacturing, 2008, 24(3): 359-369.

[9] Gorji Kandi S, Amani Tehran M, Rahmati M. Colour dependency of textile samples on the surface texture[J]. Coloration Technology, 2008, 124(6): 348-354.

[10] Zhang G, Ma Z M. Texture feature extraction and description using Gabor wavelet in content-based medical image retriecal[C]//Proceeding of the 2007 International Conference on Wavelet AnalysiS and Pattern Recognition. Beijing, 2007: 169-173.

[11] 韩润萍, 孙苏榕, 姜 玲, 等. 基于Gabor滤波器组的织物疵点检测方法[J]. 计算机工程与应用, 2007, 43(7): 211-214.

(责任编辑： 张祖尧)

A Method of Extracting Fabric Texture Feature Combined with FFT and Gabor Filter

RENJing,ZHOUHua,GUOChao,WANGYing,MEIZai-huan

(Key Laboratory of Advanced Textile Materials and Manufacturing Technology, Ministry of Education, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Extraction method of fabric texture features combined with FFT and Gabor filter was proposed in allusion to fabric texture feature extraction and characterization. 2 optimal Gabor filters were designed through extracting frequency spectrum wedge feature (the angular distribution) and ring feature (radial distribution) with FFT as characteristic angle and frequency parameter. The 2 Gabor filters were respectively convoluted with texture image of fabrics to get the target sub-image, and then fusion processing was made for the sub-image to achieve the purpose of extracting texture feature. On the premise of successfully getting the texture feature of line image, it was applied to extract common fabric texture feature and compared with traditional Gabor filter extraction method. The results show that fabric texture feature method combined with FFT and Gabor filter is effective, and the extraction result is superior to traditional method.

FFT; Gabor; fabric texture; feature extraction

1673- 3851 (2015) 01- 0006- 05

2014-06-30

任 静(1990-),女,浙江湖州人,硕士研究生,主要从事纺织计算机应用方面的研究。

周 华,E-mail:hzzh@zstu.edu.cn

TS103.7

A