基于模糊的并行Hough变换航迹起始算法*

梁志兵,王 睿,郭相科

(空军工程大学防空反导学院, 西安 710051)

基于模糊的并行Hough变换航迹起始算法*

梁志兵,王 睿,郭相科

(空军工程大学防空反导学院, 西安 710051)

由于测量误差和参数空间分割大小的影响,并行Hough变换航迹起始方法仍存在较多的杂波。针对这一问题,提出一种基于模糊的并行Hough起始算法,该算法利用不同时刻模糊函数的隶属度分别作为参数空间的累积量,继而将具有相同索引的累积量构成累加向量,再根据规则来确定累加矩阵,最后通过门限检测判断是否航迹起始。仿真实验表明,该算法可有效抑制变换误差的影响,降低虚假航迹占有率,并在密集杂波下准确地起始航迹。

并行Hough变换;航迹起始;模糊函数;隶属度;累加向量

0 引言

航迹起始是多目标跟踪的首要问题[1],其任务在于实现目标的检测和初始状态的估计[2]。现代军事迅猛发展,超高速、大机动目标不断涌现,如何实现航迹的快速、准确起始已成为现代防空作战的重要问题之一。

目前的航迹起始算法可分为顺序处理技术和批处理技术两大类[1]。前者的代表有:直观法、逻辑法[3]、修正逻辑法[4]等;后者主要包括:Hough变换及其大量的改进算法[2,5-7]。Hough变换以其对局部缺损的不敏感、对随机噪声的鲁棒性[6]等优点,广泛应用于强杂波环境下的航迹起始,但其计算量大,且不利于航迹的快速起始。

文献[2]提出了一种并行Hough变换快速航迹起始算法,与经典Hough变换相比,有效的克服了雷达单次扫描数据的累积效应,但受测量误差、参数空间分割大小等的影响,其起始结果仍存在大量的杂波。针对这一问题,文中提出一种基于模糊的并行Hough起始算法,峰值累积效果更加明显,有效降低虚假航迹占有率。

1 并行Hough变换航迹起始算法

文献[2]提出的并行Hough变换快速航迹起始算法较为有效的解决了Hough变换由于单次扫描数据的累积效应而形成虚假航迹的问题,且从图1可以看出,该算法在时间流程上是并行处理的,缩短了数据处理时间;从空间设置上,只要保证参数空间的方格容量和坐标划分相同,则各Hough变换互不影响。

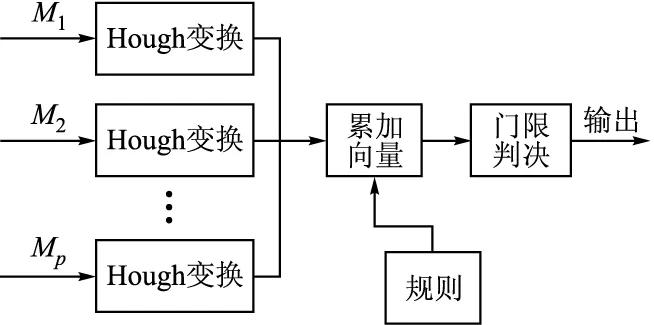
图1 并行Hough变换结构图

并行Hough变换航迹起始算法具体分3步实现:

首先将多次扫描数据集合按图1的方式进行Hough变换,并分别映射到参数空间;然后取各参数空间具有相同索引的累积量构成累积向量,再通过规则得到累积矩阵A;最后利用门限检测判断是否航迹起始。

2 测量误差对Hough变换的影响

根据Hough变换原理,假设笛卡尔坐标系中的雷达观测数据为(x,y),根据式(1)变换到参数空间中的坐标为(ρ,θ),即:

ρ=xcosθ+ysinθ

(1)

式中,θ∈[0,180°]。如果一组数据(xi,yi)属于同一直线,那么它们在参数空间中会交于一点(ρ0,θ0)。

通常将ρ-θ平面离散的分割成若干个小方格,通过3-D直方图中的峰值来判断公共的交点。直方图中每个方格的中心点[7]为:

(2)

(3)

式中:Δθ=π/Nθ,Nθ为参数θ的分割段数;Δρ=L/Nρ,Nρ为参数ρ的分割段数,L为雷达测量范围的两倍。

对点(xi,yi),根据式(1)遍历每个θn,计算出相应的ρn的估值,并对方格(ρn,θn)的计数加一。

但受参数空间分割大小的影响,传统的Hough变换会出现峰值簇拥,更重要的是当雷达测量误差较大时,累积峰值会更加不明显[8]。假设雷达测量点的坐标误差为(dx,dy),根据式(1)可得:

dρ=cosθ×dx+sinθ×dy

(4)

雷达一般只能测量径向距离和方位角,由坐标转换公式可得x=rcosβ,y=rsinβ,其中,r为雷达到目标的径向距离,β为雷达到目标的方位角,可以得到微分公式[1]:

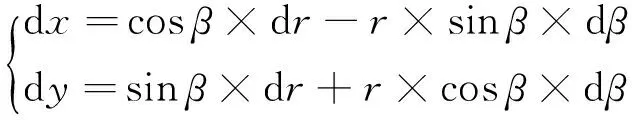
(5)

联立式(4)和式(5),可得

dρ=cos (θ-β)×dr+sin (θ-β)×r×dβ

(6)

3 基于模糊的并行Hough变换算法

3.1 基于模糊的并行Hough变换结构

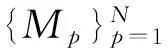
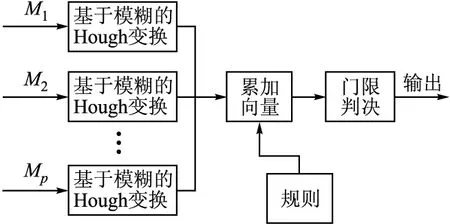
图2 基于模糊的并行Hough变换结构图

3.2 参数空间累积方式

由文中第2节可以得出,传统的Hough变换采用0-1二值累积方法,存在变换误差。针对Hough变换参数空间峰值累积的模糊性,将模糊集引入Hough变换各个样点的累积过程中。

假设第p次扫描的(ρ,θ)平面内的模糊集为Ai,p,核元素为根据式(1)和式(2)计算出的(ρi,p,θi,p),其隶属度为1。假设参数空间的间隔尺寸是Δρ和Δθ,ρ、θ方向上的最大误差范围分别为ρm和θm,Ai,p的论域为:

ρij,p=ρi,p-ρm+(j-1)Δρ,j=1,2,…,kρ

(7)

θik,p=θi,p-θm+(k-1)Δθ,k=1,2,…,kθ

式中：kθ=2θm/Δθ+1是Ai,p在θ方向上的支集元素个数,kρ=2ρm/Δρ+1是Ai,p在ρ方向上的支集元素个数。采用正态型隶属度函数:

j=1,2,…,kρ,k=1,2,…,kθ

(8)

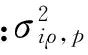
设由第p次扫描数据Mp得到的参数空间累加矩阵为Bp(ρ,θ)=(bij,p)m×n,m=1,2,…,Nρ,n=1,2,…,Nθ。在计算出(ρi,p,θi,p)后,根据式(8)计算得到的中心点附近区间的隶属度μijk,p作为Bp(ρ,θ)的累积量,即bij,p是第p次扫描参数空间的索引(i,j)的隶属度累积量。

对应于参数空间任一索引(i,j),均设累加向量[2]:

Lij=[bij,1bij,2…bij,p]T

(9)

根据上述原理,设定以下规则来对累加向量Lij进行处理:

1)根据参数空间的分割情况,初始化矩阵B(ρ,θ)=(bij)m×n,用来存储最后的累积结果。

2)设定门限q1,当累加向量Lij的各个元素均大于q1时,则令bij为Lij各个元素的和;否则,令bij=0。

由于以隶属度为累积量,峰值累积效果较为明显,所以通过一个较低门限即可滤除大量杂波,同时也不影响真实航迹,故q1设定为单次累积峰值的0.25倍。

3.3 航迹起始步骤

步骤1 将各次扫描数据按照图2进行基于模糊的Hough变换,并将结果保存在相应的累加矩阵Bp(ρ,θ)中。

步骤2 依据3.2规则对累加向量进行处理,并将处理结果保存在矩阵B(ρ,θ)中。

步骤3 设定门限q2,当bij≥q2时,则根据相应的(ρ,θ)得到相对应雷达测量数据,并起始航迹。

根据文中算法的峰值累积效果明显这一特点,q2应为峰值的0.6～0.7倍。

4 仿真分析

仿真环境[1]如下:假设有5个目标做匀速直线运动,使用一个2D雷达对这些目标进行跟踪,5个目标的初始位置分别为(55 000 m,55 000 m)、(45 000 m,45 000 m)、(35 000 m,35 000 m)、(25 000 m,45 000 m)、(15 000 m,55 000 m),它们的速度均为vx=500 m/s,vy=0 m/s。同时,假设雷达的采样周期为T=5 s,雷达的测距误差和测向误差分别为σr=200 m和σθ=0.3°。

每个扫描周期的杂波个数服从泊松分布,可通过MATLAB的poissrnd命令产生,且杂波在扫描区域内均匀分布,目标运动轨迹及杂波分布见图3。给定杂波参数λ=50,参数空间划分为Nρ=400,Nθ=200,门限q=4,γ和q2分别设定为峰值的0.8倍[9]和0.65倍。

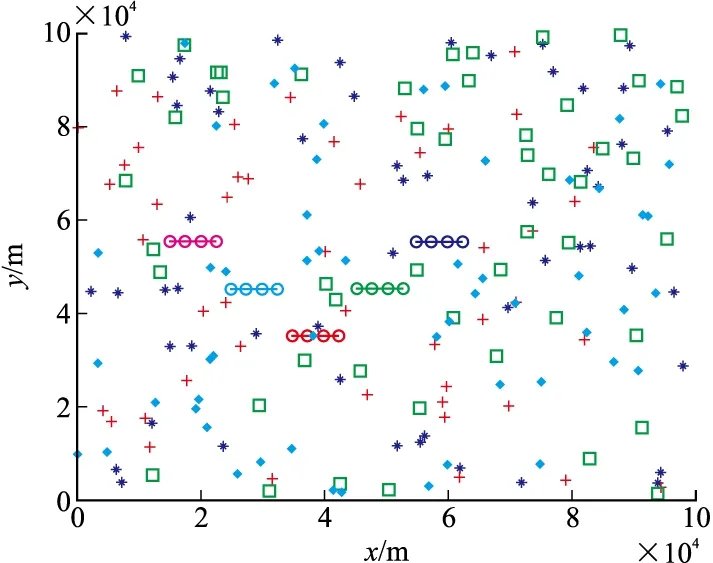
图3 目标与杂波分布图

1)各算法参数空间累积情况比较

图4给出了目标真实轨迹Hough变换、目标和杂波Hough变换、文献[2]并行Hough变换和文中提出的Hough变换在参数空间的累积图。将图4(b)、4(c)、4(d)与图4(a)进行对比,图4(c)和图4(d)的峰值累积与真实目标的峰值累积较为接近,但图4(d)的峰值累积更为明显;从峰值大小来看,图4(d)的峰值最大,分辨率最高。因此,图4(d)在峰值累积和分辨率方面均有较好的效果。

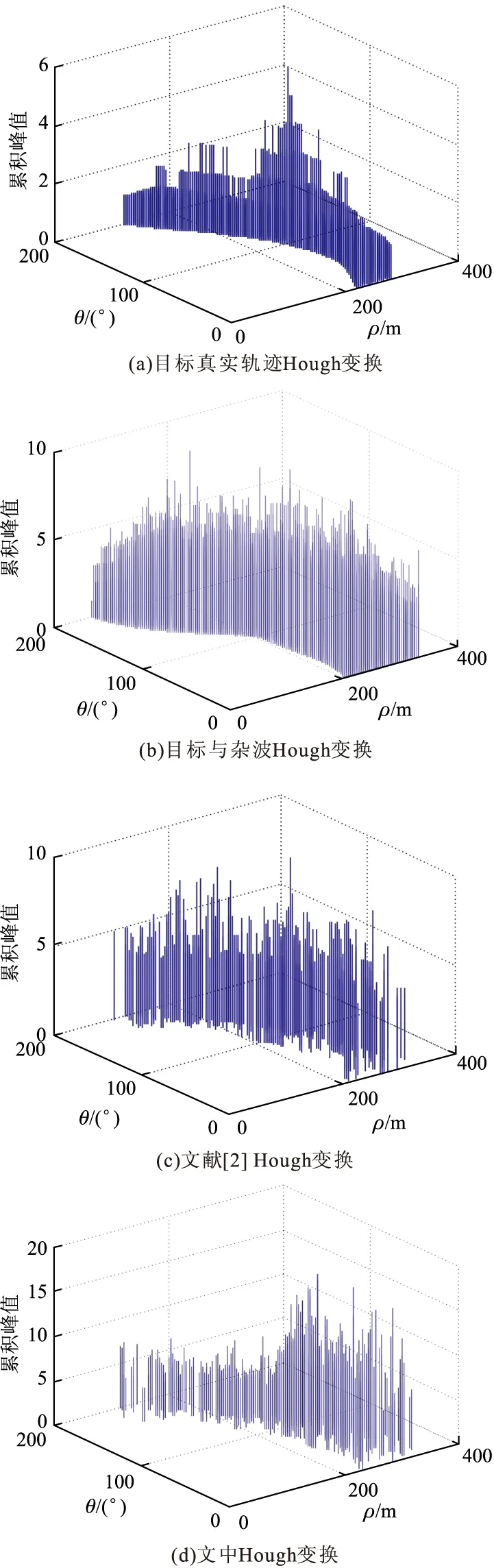
图4 参数空间累加结果图

2)各算法的航迹起始结果比较

图5给出了标准Hough变换、文献[2]算法和文中算法的航迹起始结果图,图中用直线标出了目标的真实运动轨迹。

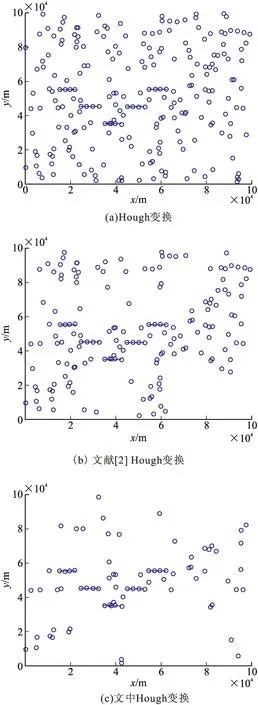
图5 航迹起始结果图

对比3幅图不难发现,3种算法均能检测出目标的真实航迹,但标准Hough变换的起始图存在大量的杂波,从而造成大量的虚假航迹;文献[2]的起始图杂波较少,但还是存在较多的虚假航迹;文中算法可有效抑制杂波的影响。

3)正确起始次数和虚假航迹占有率[10]比较

进行100次蒙特卡洛仿真,对文献[2]算法和文中算法5条航迹的正确起始次数和虚假航迹的占有率进行比较,其结果见表1和图6。

表1 正确航迹起始次数

由上可见,两种算法的平均正确航迹起始概率分别为76.8%和77.2%;虚假概率占有率分别为88.10%和81.91%。结果表明,两种算法正确起始概率相近,但文中算法将虚假航迹占有率降低了6.19%,能够有效的抑制虚假航迹的产生。

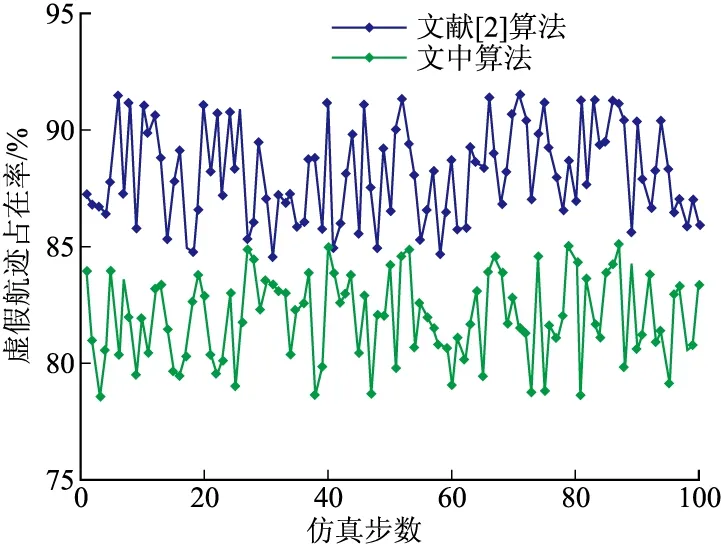
图6 虚假航迹占有率

5 结语

针对并行Hough变换快速航迹起始仍存在较多杂波的问题,文中提出了基于模糊的并行Hough变换航迹起始算法。该算法根据Hough变换参数空间峰值累积的模糊性,将模糊集引入Hough变换的累加过程中,使累积效果更为明显。从参数空间累积情况、航迹起始结果以及正确航迹和虚假航迹占有率3个方面将文中算法分别与传统Hough变换和文献[2]算法进行比较,仿真结果表明文中算法能够有效的抑制杂波的影响,降低虚假航迹占有率,且具有良好的起始效果,适合于密集杂波下目标的航迹起始。

[1] 何友, 修建娟, 关欣, 等. 雷达数据处理及应用 [M]. 北京: 电子工业出版社, 2013.

[2] 鹿传国, 冯新喜, 孔云波. 并行Hough变换快速航迹起始 [J]. 计算机工程及应用, 2013, 49(4): 5-8.

[3] 张喆, 樊晓光, 李建勋. 基于M/N逻辑和一步延迟的航迹起始方法 [J]. 计算机工程, 2011, 37(10): 234-236.

[4] 苏峰, 王国宏, 何友. 修正的逻辑起始算法 [J]. 现代防御技术, 2004, 32(5): 66-68.

[5] 贺鹏, 白亮. 快速随机Hough变换航迹起始算法 [J]. 电光与控制, 2010, 17(5): 26-29.

[6] 贺鹏, 梁彦, 金术玲, 等. 多尺度聚类Hough变换航迹起始方法 [J]. 火力与指挥控制, 2008, 33(11): 36-38.

[7] Ben-Lian Xu, Qing-Lan Chen, Zhi-Quan Wang. A new track initiation method for multi-target tracking [C]∥ IEEE Conference on Industrial Electronics and Applications, 2008: 1551-1556.

[8] 吴泽明, 任姝婕, 倪明放. 基于模糊累积函数的航迹起始问题研究 [J]. 系统工程与电子技术, 2009, 31(5): 1213-1216.

[9] 鹿传国, 冯新喜, 孔云波, 等. 并行Hough变换航迹起始 [J]. 雷达学报, 2013, 2(3): 292-299.

[10] Yan-Hang Zhang, Xiao-Hong Su, Pei-Jun Ma. Multi-Hough transform track initiation for detecting target with constant acceleration [C]∥International Symposium on Information Science and Engineering, 2008, 2: 581-584.

Parallel Hough Transform Track Initiation Algorithm Based on Fuzzy

LIANG Zhibing,WANG Rui,GUO Xiangke

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

Due to impact of radar measurement error and parameter space partition size, track initiation method based on parallel Hough transform still reveals a lot of clutter. To solve this problem, a parallel Hough transform track initiation algorithm based on fuzzy proposed. After mapping the membership degree of fuzzy logic function in different time into the parameter space separately, the accumulated results with the same index constitute an accumulated vector. According to the rules, the accumulated matrix can be obtained. Finally, we a decision on whether to initiate the track or not through the threshold detection. Simulation results show that this algorithm can constrain of mapping error effectively, decrease the occupancy of false tracks and initiate the track accurately under dense clutter environment.

parallel Hough transform; track initiation; fuzzy function; membership degree; accumulated vector

2014-09-09

TN953

A

作者间介:梁志兵(1990-),男,山西吕梁人,硕士研究生,研究方向:多目标跟踪与信息融合。