基于自适应滤波算法的磁强计/陀螺组合误差修正*

王嘉雨,曹红松,白 松,张宪国

(中北大学机电工程学院,太原 030051)

基于自适应滤波算法的磁强计/陀螺组合误差修正*

王嘉雨,曹红松,白 松,张宪国

(中北大学机电工程学院,太原 030051)

针对弹箭姿态测量中低精度陀螺姿态解算误差因漂移迅速增大的问题,文中采用三轴磁强计和陀螺组合测姿方案,对姿态角的输出进行修正。通过建立基于陀螺姿态解算误差角的状态方程和磁强计输出的误差观测方程,采用自适应卡尔曼滤波方法以抑制滤波发散并对姿态误差角进行估计。仿真结果表明:该方法能有效利用磁强计的输出抑制了陀螺漂移带来的误差,提高解算精度,满足长时间姿态测量的要求。

磁强计;陀螺;自适应卡尔曼滤波;组合姿态测量

0 引言

磁强计、微机械陀螺等低成本高集成度的传感器元件在武器弹药精确化的过程中有着明显的优势和潜力,所以采用敏感元件的弹箭姿态测量方法成为近年来研究较多的课题[1]。但是微机械陀螺精度低,单一使用难以满足长时间姿态测量要求,而单独使用三轴磁强计无法完成载体相对参考坐标系的姿态测量[2]。

利用磁强计与微机械陀螺形成组合弹箭姿态测量系统是一个合适的选择,它能够综合陀螺短时间的高精度和磁强计的无漂移特性[3]。由此文中提出一种基于三轴微机械陀螺与磁强计的组合弹箭姿态测量方法,该方法利用微机械陀螺的输出实时解算姿态信息,然后依据建立的误差角状态方程,以磁强计的输出作为姿态误差角的观测量,使用自适应卡尔曼滤波方法对姿态误差角进行估计,并对陀螺解算的姿态进行修正,该方法使用灵活,能够有效抑制陀螺漂移,具有较高的精度。

1 姿态解算和误差模型

文中姿态解算使用的参考坐标系为地理坐标系(O-xnynzn),即常用的东-北-天坐标系。

弹体姿态解算方法采用解姿态矩阵微分方程的方法,其公式如下:

(1)

采用四阶毕-卡逼近求解之:

(2)

考虑姿态解算误差,由真实姿态到解算姿态的转换矩阵为:

(3)

φ=(φxφyφz)T为姿态误差角。两姿态之间的相对转动角速率之差为:

(4)

其中:ωc为陀螺输出值;ωa为载体相对参考坐标的真实转动角速率。设ωc与ωa之间的差值为角速率测量误差ξ,这里将其视为白噪声和一阶马尔科夫过程的叠加:

ξ=ξg+wg

(5)

(6)

Tg为相关时间常数,wg与wξ均为白噪声。

若以φ和ξg作为姿态误差方程的状态变量,则由式(4)～式(6)可以得出系统误差方程为:

(7)

设Bn为地磁矢量在参考坐标系下的矢量,Bc为磁强计输出值,考虑其误差,有:

(8)

测量误差v视为均值为零的白噪声。

(9)

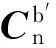
(10)

则根据式(8)～式(10)可得观测方程:

(11)

2 对姿态误差的修正

考虑到陀螺及磁强计输出中包含的噪声并不为严格的白噪声,且其统计特性无法精确获得。为避免由此带来的滤波器易发散的问题,文中使用一种能够在线估计噪声统计特性的自适应卡尔曼滤波算法,它通过观测值间接推算出自适应滤波增益,使得滤波具有良好的收敛性质。

将得出的系统误差状态方程和观测方程离散化:

Xk=φk,k-1Xk-1+Wk-1

Zk=HkXk+Vk

(12)

其中:

该自适应滤波算法的具体原理是根据观测量Zk估计出相关函数序列Ck,再由Ck推算出最优稳态增益矩阵K,使增益K不断与实际测量数据Zk相适应[6]。

假设观测量Zk具有各态历经性,则其相关函数序列的估计为:

(13)

又因为相关函数满足关系式:

(14)

可得:

(15)

增益矩阵是以卡尔曼滤波的最优增益矩阵为基础的,可表示为:

(16)

式中只有Sk为未知量,由于:

(17)

最后有估计方程:

(18)

3 对修正算法的仿真验证

仿真实验以太原为仿真背景地点,以某型国产MEMS陀螺和HMC1043三轴磁强计的参数指标对陀螺和磁强计信号进行模拟。该地区磁场强度的地理坐标系分量为:Bn=10-4×[-0.02160.309-0.43]T,陀螺漂移1°/s,分辨率0.05°/s,时间常数Tg=360 s,白噪声方差0.1°/s,磁强计分辨率1.2×10-8T,白噪声方差10-4T。

为在计算机中模拟陀螺角速率输出,这里假设弹体姿态参数的变化规律为:俯仰角ϑ=π/4-0.1sin 0.2t,偏航角ψ=π/4,滚转角γ=πt,则陀螺的理想输出为:

(19)

实际输出根据上述噪声参数加入随机漂移量和白噪声。磁强计参考输出为Bn在弹体坐标上的投影,并加入白噪声。姿态解算步长0.005 ms,滤波器步长0.01 ms,仿真时间14 s,仿真曲线图如图1～图3。

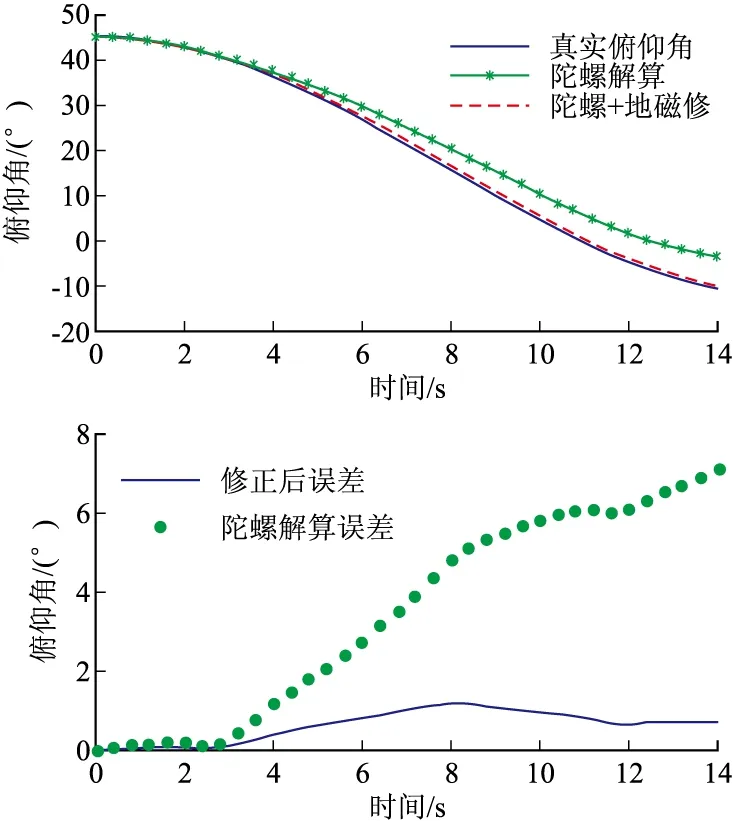
图1 俯仰角仿真结果曲线

图2 滚转角仿真结果曲线

图3 偏航角仿真对比曲线

图1～图3为未经修正的陀螺单独解算姿态角、地磁+陀螺组合解算的姿态角和弹体实际姿态的仿真曲线图,以及相应的误差比较曲线。从图中可以看出,随着时间增长,陀螺单独解算的姿态误差迅速积累,误差角呈发散趋势或存在较大振荡;而经过地磁传感器校正的地磁+陀螺组合解算的结果,解算的姿态角的误差量没有出现明显的增大趋势,始终较好的贴合了实际姿态曲线,滤波收敛度良好,最大误差角均不超过2°,满足弹箭姿态测量的精度指标,说明滤波算法有效抑制了陀螺随机漂移带来的姿态角解算发散,提高了姿态解算精度。

4 结论

文中提出的方法是以陀螺输出量对弹体姿态进行解算,通过建立陀螺解算的姿态误差角状态方程和磁强计输出为观测量的观测方程,使用自适应卡尔曼滤波方法对误差角进行估计,并对解算结果进行修正。从仿真结果看:采用陀螺与磁强计的组合测姿方法相对陀螺单独解算的姿态精度有了明显提高,而且无需借助其他辅助信息,误差量稳定,说明了算法的有效性和方案的简便性。但该方法只经过数值仿真的验证,实际影响解算精度的因素则要多很多,如陀螺建模的误差,磁场干扰等等,因此还需要大量的实测数据支持和进一步的分析研究。

[1] 曹红松, 冯顺山, 赵捍东, 等. 地磁陀螺组合弹药姿态探测技术研究 [J]. 弹箭与制导学报, 2006, 26(3): 142-145.

[2] 鲍亚琪, 陈国光, 吴坤, 等. 基于磁强计和MEMS陀螺的弹箭全姿态探测 [J]. 兵工学报, 2008, 29(10): 1227-1231.

[3] 黄旭, 王常虹, 伊国兴, 等. 利用磁强计及微机械加速度计和陀螺的姿态估计扩展卡尔曼滤波器 [J]. 中国惯性技术学报, 2005, 13(2): 27-34.

[4] 晏登洋, 任建新, 宋永军. 惯性/地磁组合导航技术研究 [J]. 机械与电子, 2007(1): 19-22.

[5] 吴锦杰, 刘昆, 石实, 等. 基于磁强计和光纤陀螺的小卫星姿态确定非线性滤波算法 [J]. 国防科技大学学报, 2013, 35(1): 1-6.

[6] Haykin S. Adaptive filter theroy [M]. Beijing: Publishing House of Electronics Industry, 2002.

[7] Crassidis J L, Markley F L. Unscented filtering for spacecraft attitude estimation [J]. Journal of Guidance, Control and Dynamics, 2003, 26(4): 536-545.

Research on Integrated Error Correction of Magnetometers and Gyroscope Using Adaptive Filtering

WANG Jiayu, CAO Hongsong, BAI Song, ZHANG Xianguo

(School of Mechatronics Engineering, North University of China, Taiyuan 030051, China)

As for attitude measurement of missiles, low-precision gyroscope can not get satisfactory accuracy. For this reason, an integrated attitude measurement method was used to correct output of attitude angle, the state equation of attitude error angle and the error observation linear equations that based on the outputs of three-axis magnetometer were built, an adaptive filtering method was used to estimate error angle optimally and correct the output of attitude angle. The simulation results show that this method suppresses the error caused by gyroscope drift effectively by using the output of magnetometer and improves the accuracy of the attitude solver, satisfying the requirement of longtime attitude measurement.

magnetometer; gyroscope; adaptive Kalman filtering; integrated attitude measurement

2014-04-04

王嘉雨(1991-),女,陕西富平人,硕士研究生,研究方向:智能控制。

TN397

A