水下基于层级的约束加权最小二乘时差定位*

2015-05-06薛建彬陈一鸣何凤婕

传感技术学报 2015年2期

关键词：信标测距定位精度

薛建彬,陈一鸣,何凤婕

(1.兰州理工大学计算机与通信学院,兰州 730050;2.东南大学移动通信国家重点实验室,南京 210096)

水下基于层级的约束加权最小二乘时差定位*

薛建彬1,2*,陈一鸣1,何凤婕1

(1.兰州理工大学计算机与通信学院,兰州 730050;2.东南大学移动通信国家重点实验室,南京 210096)

针对距离无关定位算法与距离相关定位算法中定位精度的问题,分析了误差对定位性能的影响及影响误差的因素,在最小二乘定位算法的基础上,提出了一种基于层级结构的约束加权最小二乘时差定位算法。该算法利用AUV(Autonomous Underwater Vehicle)对水下节点进行分层,使得具有层级和深度信息的信标节点升降至未知节点所在平面,从而将三维定位转换为二维定位,降低了算法的复杂度,同时避免了距离未知节点较远的信标节点对定位的影响,提高了测距精度,使定位误差进一步降低。仿真结果表明,该算法在位置误差较小的情况下,可以明显地提高定位精度。

水下无线传感器网络;时差定位算法;约束加权最小二乘算法;距离无关定位;距离相关定位

无线传感器网络是由大量廉价的传感器节点以动态自组织的方式构成的无线通信网络,通过传感器节点对监测区域内的事件信息进行感知、测量和采集,并反馈给用户,从而实现对监测区域的实时监测[1]。水下传感器网络(UWSN)作为陆地无线传感器网络的重要拓展,在水资源环境保护、海洋灾害预警、辅助导航、军事防控以及海洋资源开发等众多领域都有着重要作用。对于水下传感网络所有的感知数据都需要准确的位置信息作为支撑,因此对水下传感网络节点定位技术的研究有着重要的作用和意义。

目前对水下传感网络节点定位的研究,集中在无线传感网络定位算法的基础上,根据水下应用环境、网络规模和节点能量,同时结合水声信道的特点,最终确定并设计出符合水下环境的定位算法。这些已有的算法主要分为距离无关算法和距离相关算法两大类[2-3]。基于距离无关的定位算法根据网络的连通性等信息估算节点的位置。Shrawan Kumar D K Lobiyal[4]等人在DV-Hop算法的基础上引入加权最小二乘算法修正每跳平均距离,从而减小锚节点到未知节点的固有误差,提高未知节点的定位精度。魏先民[5]等人对未知节点寻找一个由k个信标节点组成的多面体,使节点位于这个多面体的内部,根据信标节点的位置信息求得该多面体的质心,以此坐标作为节点的近似坐标。该类算法中节点不需要额外的测距设备,因此具有简单、成本低的优点,但是距离无关定位技术的定位精度比较低。在距离相关的定位技术中,节点通过传播含有距离的信号,估算出其与锚节点的距离,再利用距离相关算法得到未知节点的位置。焦小涛[6]等人分析了基于TDOA的两种定位算法:Chan算法和Taylor算法。Chan算法在噪声服从高斯分布的环境下,定位精度高,但在非视距环境下,Chan算法的定位精度显著下降。Taylor算法通过在递归中求解TDOA测量误差的局部最小二乘解来改进估计位置,但定位精度取决于定位初始值。文献[7]中Zheng Jungang等人利用信号接收强度RSSI对未知节点到信标节点的距离进行估计,并针对RSSI测距技术的不足,提出了在监测区域内引入4个已知坐标的信标节点加强信号的接收强度,提高测距精度。这类定位算法较为复杂但却提高了定位精度。

本文通过信号到达时间差(TDOA)得到一组非线性方程组,通过引入中间变量将其转换为线性方程组,在最小二乘定位算法的基础上,利用约束条件对第1次得出的估计位置进行优化,并提出了分层[8]的概念。通过AUV对水下节点进行分层,避免距离未知节点较远的信标节点参与定位,降低了测量误差对定位性能的影响,提高了定位的精度程度。

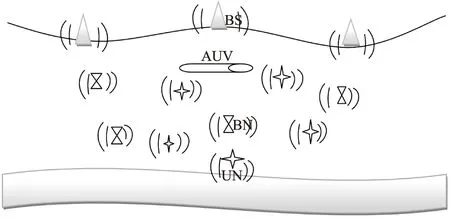
图1 水下传感网络定位模型

1 算法原理和算法描述

1.1 水下传感网络定位模型

在图1所示的水下传感网络定位模型中,基站是部署在水面之上具有全球定位系统(GPS)的卫星节点。信标节点和未知节点携带了深度传感器被随机的抛洒至监测水域中,信标节点可以与基站直接通信实现节点的自定位。未知节点由于受到通信带宽,能耗等其他限制因素的影响,不能与基站直接通信,但可以用已知坐标的信标节点实现定位。AUV具有自主导航、实时监测和功率控制能力,因此当AUV潜行至目标水域后通过功率控制实现监测区域内所有节点的分层。属于同一层级的节点具有良好的连通性,可以直接通信。

1.2 约束加权最小二乘的时差定位算法

在监测水域中,未知节点的位置用(x,y)表示,信标节点(BNi)的位置用(Xi,Yi)表示(其中i的取值为0,1,2,…,N),N为参加定位的信标节点个数。测距信号到达的时间用ti表示,信标节点与未知节点的距离用di表示,那么TDOA的测量值ti,0为信号到达BNi与BN0的时间差,di,0表示未知节点到BNi与BN0的距离差,则:

(1)

由di,0=cti,0=di-d0,c为声速,得到

(2)

当i=1时,式(2)为:

(3)

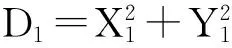
(4)

将式(4)用矩阵表述为:

AX=b

(5)

其中

在上述线性方程中,由于误差的存在,式(5)在通常情况下无解,但是在最小二乘的意义下,我们可以求出方程的最小二乘解[9]。方程的解为:

(6)

再此对影响定位的误差进行分析:

(7)

对式(7)两边同时全微分得到

(8)

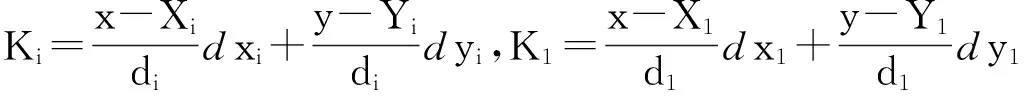
将式(8)用矩阵形式表述为:

dR=HdX+dS

(9)

得到

dX=(HTH)-1HT(dR-dS)

(10)

其中

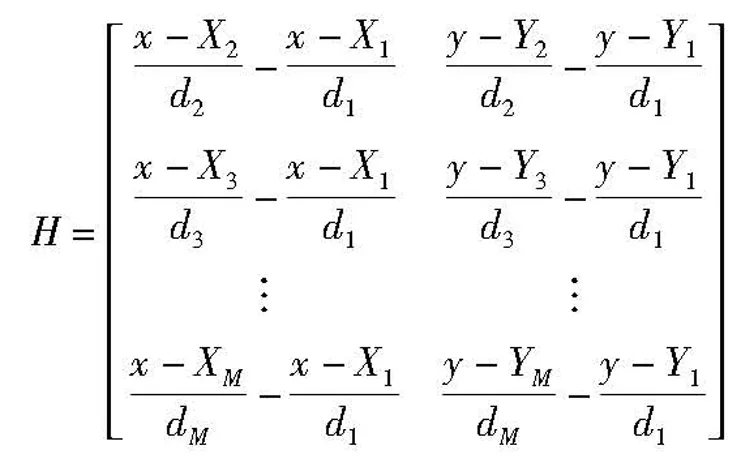
dR表示时差测量误差,

dR=[dd2,1,dd3,1,…,ddM,1]T

dX表示未知节点的定位误差,

dX=[dx,dy]T

dS表示站址误差,

因此未知节点的定位误差与时差测量误差、信标节点的布站形式以及站址误差有关[10-11]。当我们只考虑时差测量误差,不考虑信标节点的站址误差时,由式(5)得到误差方程:

ε=b-AX

(11)

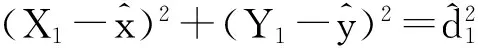
(12)

式中Σ=diag(1,1,-1)。相应的代价函数为

L(x,λ)=(b-AX)TW-1(b-AX)+λxT∑x

(13)

1.3 基于层次结构的水下定位算法

AUV可以通过预先设定的路线在水下监测区域中航行,并且具有自我控制发射功率的能力。在本算法中AUV导航至监测区域中,利用不同的信号发射功率广播信号对节点分层。在自由传播环境中,信号的发射功率与信号所覆盖的区域半径之间的公式[12-13]可用式(14)描述:

(14)

其中:Ps是信号的发射功率,Pr是接收信号的接收功率,f是发射功率,d是信号发射源到信号接收源的距离,c是光速。从式(14)中可以看出当信号接收功率一定时,信号的发射功率与信号的传播距离成正比关系。如果我们将信号的发射功率设为级别R[14](R的级别为R1,R2,R3……),那么信号的覆盖范围随着发射功率级别的增大而增大,这样水下监测区域按照发射功率级别R分为不同的层级,每一层级是以AUV为圆心,Ri-1为内径、Ri为外径的球壳型区域。

未知节点发出定位信号,定位信号中包含了未知节点所在的层级和深度信息,AUV接收到后提取出信息,根据相应层级所对应的功率广播定位信号至信标节点。信标节点接收到定位信号,首先通过深度调节功能,使自己上升或下潜到未知节点所在的平面。这样就将三维环境中的定位转换为二维平面定位,如图2所示。

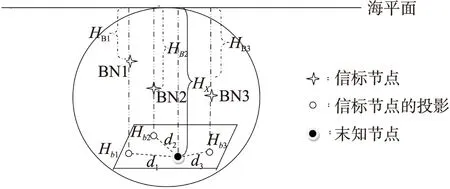
图2 将三维定位转换为二维定位

假设未知节点至少接收到三个信标节点的测距信号,根据距离公式可以得到式(15):

(15)

将式(15)展开并转换为矩阵表达形式:

AX=B

(16)

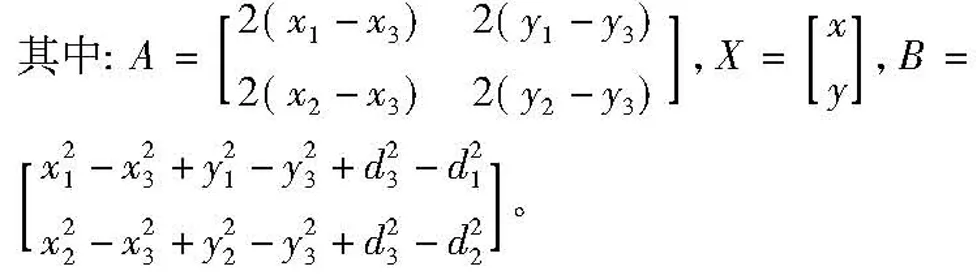
由于在测距过程中避免不了误差的存在,首先利用最小二乘原理使得误差最小化

‖AX-B‖2=(AX-B)T(AX-B)

=XTATAX-2BTAX+BTB

(17)

在式(17)中设h(x)=XTATAX-2BTAX+BTB,对x求导并令其等于0得到未知节点第一次估计值

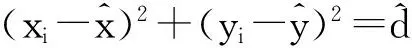
2 仿真实验

仿真环境为100m×100m×100m的三维空间,假设有20个信标节点和120个未知节点在空间中随机的部署,未知节点通过定位算法得到位置信息后转换为信标节点,并参与其它未知节点的定位。所有节点的通信半径为25m,测距误差是节点通信半径的1%。以均方根误差作为定位精度的指标,通过仿真实验对测距误差对定位精度的影响与传感器位置误差对定位精度的影响两个方面进行分析。

如图3所示监测水域中未知节点个数不断增加时,两种定位算法对未知节点定位的均方根误差也不断增大。在三维水下环境中,由于存在多径干扰、多普勒频移以及信标节点自身误差的影响,直接利用最小二乘定位算法使得误差不断累积,导致均方根误差不断增大。而基于层级的约束加权最小二乘定位算法首先利用层级与深度信息,将信标节点上升或下降至未知节点所在平面,将三维立体定位转换成为二维平面定位,降低了水下复杂环境对定位精度的影响。但是由于信标节点自身位置存在误差,使得未知节点增加时,累积误差也会不断增加,从而均方根误差不断增大。图中可以看出最小二乘定位算法计算出来的误差平均在5m左右,而基于层级的约束加权最小二乘算法计算出来的误差平均在3m左右。因此,本文提出的基于层级的约束加权最小二乘定位算法改善了定位算法的性能。

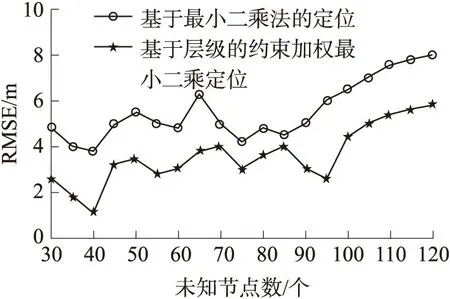
图3 均方根误差比较

在算法中节点的测量误差对定位准确度的影响,可以通过改变测量误差的范围进行仿真实验。将测量误差占通信半径的百分比设为1%～10%,最后取50次测量结果的平均值。

图4中可以看出,当测距误差占通信半径的比例逐渐增大时,两种算法的均方根误差也不断增大,导致算法的定位性能下降。基于最小二乘的时差定位算法,在不考虑信标节点的位置误差下,通过引入中间变量将非线性方程组转换为线性方程,并在最小二乘法的意义下求解得到最小二乘解,同时随着测距误差所占节点通信半径的比例不断增大,导致误差不断累积,因此均方根误差也随之增大。本文提出的基于层级的约束加权最小二乘定位算法在测距误差比例增加时,也呈现出增大的现象,但是与最小二乘时差定位算法相比,其增长趋势相对缓慢。首先AUV在对节点分层时,由于每一层级的发射功率对应着相应的距离范围,这样对未知节点定位限制了区域范围,防止距离未知节点较远的信标节点参与定位增大测距误差;其次在得到最小二乘解时,利用拉格朗日约束方程使得误差方程标准最小化求得最优估计坐标,因此均方根误差的增长速度比较缓慢。

图4 测距误差对均方根误差的影响

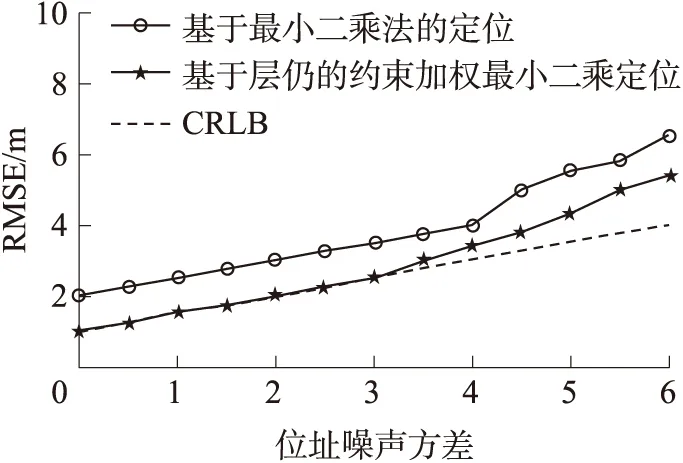
图5 位址误差对均方根误差的影响

根据矩阵公式dR=HdX+dS可知,信标节点的位址误差也会影响定位误差的精确度,因此在测量误差为节点通信半径的1%时,改变信标节点的位址误差。通过仿真实验,对本文提出的算法进行验证。

由图5可以看出,最小二乘算法的均方根误差始终达不到CRLB,而本文提出的基于层级的约束加权最小二乘算法在σ>2.5时,性能开始发散。这主要是因为最小二乘算法在信标节点自身存在误差的情况下,无法给出方程的最优解,因此最小二乘算法的定位精度无法达到CRLB。基于层级的加权最小二乘算法是将在最小二乘意义下的解,利用拉格朗日约束方程进一步优化减小误差,提高定位精度。但是当信标节点的位址误差不断增大至σ=2.5时,算法性能也开始发散。故该算法只适合在位址误差较小的情况。

3 结论

本文主要研究了水下传感网络的节点定位问题,以基于最小二乘的时差定位算法为基础,通过分析影响定位误差的因素,提出了基于层级的约束加权最小二乘定位算法。该算法首先通过AUV对节点进行分层,当未知节点请求定位时,就可以通过其所在层级的信标节点上升或下潜到同一水平面,利用约束加权最小二乘算法进行定位。仿真实验表明,在忽略位址误差而测距误差不断增大的情况下,该算法的定位性能优于最小二乘算法;当测距误差固定而存在位址误差时,该算法起初能够达到CRLB下限而在σ>2.5时性能发散,因此该算法适合在水下位址误差较小的情况,仿真实验表明该算法的定位精度相对于最小二乘定位有了较大的提升。由于水下环境复杂,伴随着洋流、潮汐的影响,节点的位置经常发生变化,如何在动态环境中提高节点的定位精度是接下来研究的重点问题[15]。

[1] 毕京学,郭英,甄杰,等.水下无线传感器网络定位技术研究进展[J].导航定位学报,2014,2(1):41-46.

[2]Kerri Stone,Tracy Camp.A Survey of Distance-Based Wireless Sensor Network Localization Techniques[J].International Journal of Pervasive Computing and Communications,2012,8(2):158-183.

[3]张宛怡.无源测向与时差定位技术研究[D].成都:电子科技大学信息与通信工程,2013.

[4]Shrawan Kumar D K Lobiyal.An Advanced DV-Hop Localization Algorithm for Wireless Sensor Networks[J].Wireless Pers Commun,2013,71(2):1365-1385.

[5]魏先明.基于多面体质心算法的水下传感器网络定位[J].计算机科学,2012,39(5):102-105.

[6]焦小涛,李建昌,门丽娟.两种TDOA定位算法在水声被动定位下的精度分析[J].电声技术,2013,37(1):73-75.

[7]Zheng Jungang,Wu Chengdong,Chu Hao.An Improved RSSI Measurement in Wireless Sensor Networks[J].Procedia Engineering,2011(15):876-880.

[8]蒋鹏,覃添,陈岁生.基于AOA降维和同心圆定位的三维传感器网络节点自定位方法[J].传感技术学报,2012,25(7):999-1006.

[9]So H C,Lin L.Linear Least Squares Approach for Accurate Received Signal Strength Based Source Localization[J].IEEE TSP,2011,59(8):4035-4040.

[10]Liu L,Wu X,Zhu Z,et al.A Localization Algorithm Based on Beacon Error Problem in Underwater Wireless Sensor Network[C]//Communication Technology(ICCT),2013 15th IEEE International Conference on IEEE,2013:478-482.

[11]马艳,于文娟,石星.节点扰动对最小二乘的UWSAN目标定位的影响[J].西北工业大学学报,2012,30(2):217-221.

[12]Krishna C R,Yadav P S.A Hybrid Localization Scheme for Underwater Wireless Sensor Networks[C]//Issues and Challenges in Intelligent Computing Techniques(ICICT),2014 International Conference on IEEE,2014:579-582.

[13]单志龙,胡燕.基于相交环的水下无线传感网络节点自定位研究[J].传感技术学报,2012,25(4):536-540.

[14]Han G J,Jiang J F,Shu L,et al.Localization Algorithms of Underwater Wireless Sensor Networks:A Survey[J].Sensors,2012,12(2):2026-2061.

[15]Zhou Z,Peng Z,Cui J H,et al.Scalable Localization with Mobility Prediction for Underwater Sensor Networks[J].IEEE Transactions on Mobile Computing,2011,10(3):335-348.

The Constraint Weighted Least-Squares Algorithm of TDOA Based on Hierarchy in Underwater Sensor Wireless Network*

XUEJianbin1,2*,CHENYiming1,HEFengjie1

(1.College of computer and communication,Lanzhou University of Technique,Lanzhou 730050,China;2.National Mobile Communications Research Laboratory,Southeast University,Nanjing 210096,China)

With reference to the position accuracy in range-based and range-free location algorithm,we analyze error effect on the performance of localization and factors that influence the error.On the basis of least squares algorithm,we propose on the constraints of the weighted least squares algorithm of TDOA based on hierarchy.The algorithm using the AUV(Autonomous Underwater Vehicle)to stratified of underwater nodes,making beacon nodes with hierarchy and depth of information of unknown nodes lift the plane,which will be converted from three-dimensional positioning to two-dimensional localization.It reduces the complexity of the algorithm,at the same time avoids the influence of the beacon nodes far from unknown nodes for positioning improves the ranging precision,to further reduce the positioning error.The simulation results show that the proposed algorithm under the condition of the position error is smaller,which can significantly improve the positioning accuracy.

UWSNs;TDOA;the Constrained weighted least squares algorithm;range-free location;range-based location