基于Matlab的一种新型折臂式门架结构分析
2015-05-06赵子涵贾英杰詹隽青李红勋孟祥德
赵子涵,贾英杰,詹隽青,李红勋,孟祥德
(1.军事交通学院 研究生管理大队,天津300161;2.军事交通学院国家应急交通运输装备工程技术研究中心,天津300161)
近年来集装箱运输得到普遍推广,作为一种 集装箱场地装卸和搬运装备,集装箱装卸搬运机(以下简称搬运机)开始得到广泛应用。受集装箱尺寸限制,搬运机的横向跨度普遍较大,因此,市场上主流的搬运机大多采用具有良好的承载能力和刚度的门架式结构单元。随着集装箱运输的不断发展,对搬运机的操作性、机动性以及装卸效率也提出了新的要求,而传统的门架式搬运机在使用过程中逐渐暴露出转向稳定性差、装卸效率较低等问题[1]。本文在分析传统门架结构缺陷的基础上,提出一种新型折臂式门架结构,并对此进行运动学和动力学分析,其结果可为折臂式门架作业方案的制订提供理论依据。
1 折臂式门架结构设计
传统门架一般采用多级伸缩式结构(如图1所示),而当前多级举升技术还不够成熟,各级举升臂之间的伸缩间隙较大,搬运机的门架完全展开后高度和横向跨度较大,因而在搬运机作业过程中难以准确控制门架,导致搬运机出现转向稳定性差、集装箱对位困难等问题[2]。
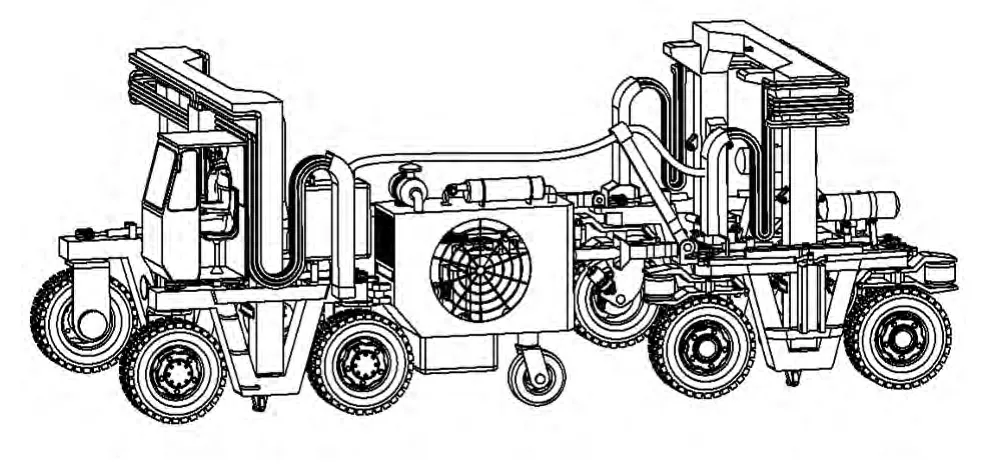
图1 某型采用多级伸缩式门架的搬运机
折臂式门架(如图2所示)主要由1个横梁、4个举升臂和3个液压缸组成。门架在展开或者收拢时,由液压缸提供驱动力,当门架完全展开后,用销轴将各部件锁死,整个门架固联成一个刚性较强的整体。
2 展开过程的运动学分析
2.1 折臂式门架的展开原理
折臂式门架是通过3个液压缸的循环交替作业驱动门架展开,因此可以将整个展开过程分解为若干个独立的子展开过程,每个子展开过程又按照“右下液压缸—左下液压缸—上液压缸”的动作顺序依次进行作业,即首先由右下液压缸推动右下举升臂展开一定角度,然后由左下液压缸推动左下举升臂展开相同角度,最后由上液压缸将门架调平。本文以一个子展开过程为例,按照其作业顺序将其分成3个阶段,对每个阶段展开独立分析。
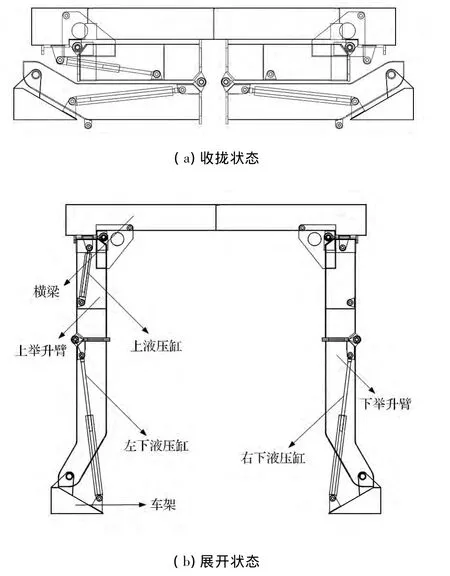
图2 折臂式门架
2.2 门架的运动学分析
下面以右下液压缸作业过程为例,将坐标变化矩阵法[3]引入到门架各铰点的确定中,从而建立起以液压缸推动举升臂的展开角度为设计变量、以门架各铰点为目标函数的数学模型。
如图3所示,AB、BC、HD、DM为门架的4个举升臂,JK、IQ、PN 为门架的3个液压缸,NM、CL为横梁,G为横梁质心。分别以点A、B、C建立坐标系 x1Ay1、x2By2、x3Cy3,AB 与水平线夹角为 α,BC与水平线夹角为β,CD与右上臂夹角为γ。
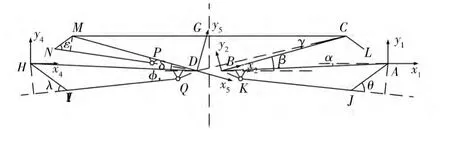
图3 折臂式门架运动学分析示意
在该过程中,左下液压缸和上液压缸均锁死,因此在该展开过程中坐标系x3Cy3中点的坐标均为常数。点C、点M和点G在坐标系x3Cy3中的坐标为(0,0)、(Mx3,My3)和(Gx3,Gy3),则点 C、点 M和点G在坐标系x1Ay1中的坐标分别为

在该过程中点C绕点D作圆周运动,由此可得
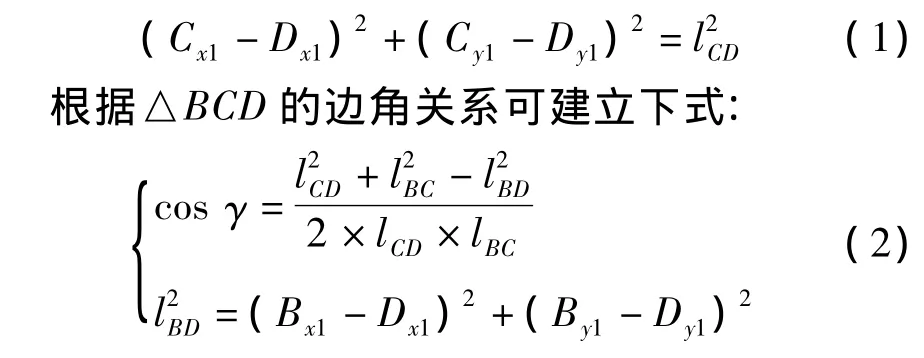
由式(1)和式(2)可分别得到β关于α的关系式β=f(α)和γ关于α的关系式γ=f(α),从而推出该过程中点C、点M和点G在坐标系x1Ay1中的坐 标:Cx1,Cy1=f(a);Mx1,My1=f(α);Gx1,Gy1=f(α)。
同理,在左下液压缸作业过程中,右下液压缸和上液压缸均锁死,以点H和点D建立坐标系x4Hy4和x5Dy5,以HD与水平线夹角φ为自变量,按照上述分析步骤,可得该过程中点C、点M和点G 在坐标系 x4HY4中的坐标:Cx4,Cy4=f(φ);Mx4,My4=f(φ);Gx4,Gy4=f(φ)。
在上液压缸作业过程中,以DM与水平线夹角δ为自变量,可得该过程中点C、点M和点G在坐标 系 x4Hy4中 的 坐 标:Cx4,Cy4=f(δ);Mx4,My4=f(δ);Gx4,Gy4=f(δ)。
由此,在折臂式门架3个展开阶段中分别建立了以液压缸展开角度(分别为α、φ和δ)为设计变量、以各铰点位置为目标函数的数学模型。
3 展开过程的动力学分析
根据展开过程中门架的受力情况(如图4所示),以右下液压缸作业过程为例,在前文分析基础上,建立以液压缸展开角度为设计变量、以各液压缸驱动力和门架铰点受力为目标函数的数学模型。
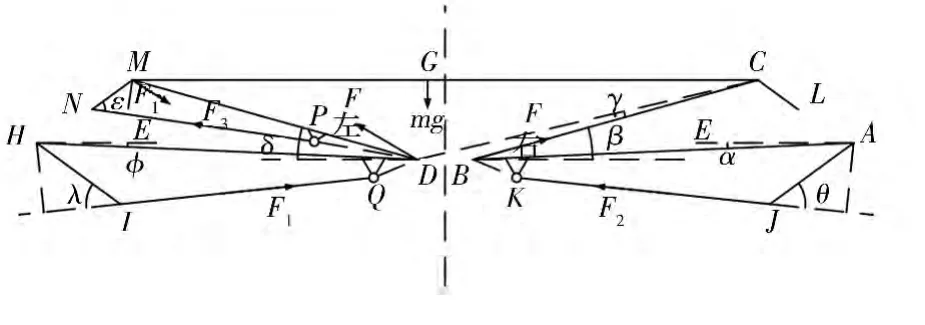
图4 门架受力示意
由受力分析可知,横梁和上举升臂主要承受自身重力mg、点B的支反力F右以及点D的支反力F左,根据力和力矩平衡关系可列方程:
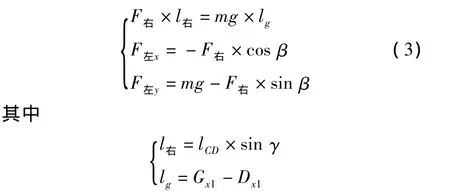
由前文分析知,γ、Gx1和β均可以表示为关于α的函数,故由式(3)可得F右和F左关于α的关系式。
以左下举升臂为研究对象,其中F1为左下液压缸驱动力,lF1为F1的力臂,列平衡方程:
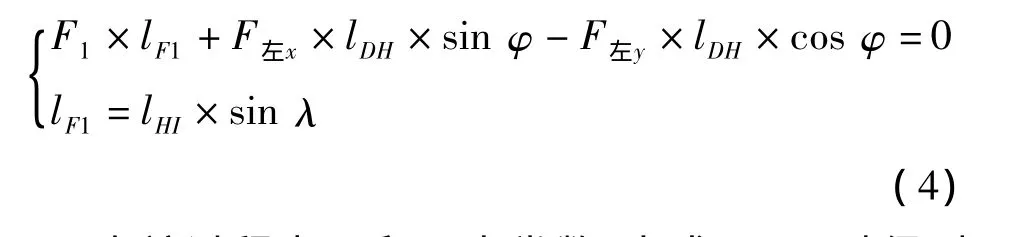
在该过程中φ和λ为常数,由式(4)可以得到F1关于α的函数F1=f(α)。
以右下举升臂为研究对象,其中F2为右下液压缸驱动力,lF2为F2的力臂,以点A为中心,列力矩平衡方程:


式中∠JAE、∠KAB均为常数。
将式(6)代入式(5)可以得到F2关于α的函数 F2=f(α)。
以左上举升臂为研究对象,其中F3为上液压缸驱动力,lF3为F3的力臂,以点M为中心,列力矩平衡方程:

由式(7)可以得到F3关于α的函数F3=f(α)。
由此在右下液压缸作业过程中建立了以α为设计变量,以 F右、F左、F1、F2和 F3为目标函数的数学模型。
同理,依次在左下液压缸作业过程和上液压缸作业过程中分别建立以φ和δ为设计变量,以F右、F左、F1、F2、F3为目标函数的数学模型。
4 展开过程仿真分析
4.1 仿真参数设定
考虑到在每个子展开过程的3个阶段中数学模型的设计变量分别为α、φ和δ,故设定各液压缸驱动举升臂的展开速度为1(°)/s,通过将时间t作为变量将各阶段加以整合,具体仿真参数设置见表1,模型中涉及的主要尺寸参数见表2。
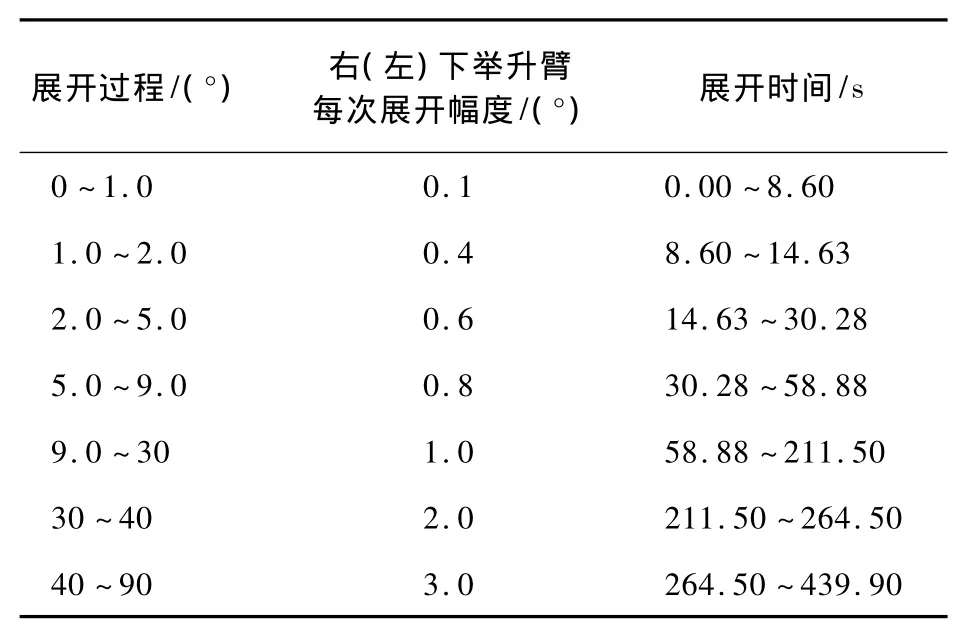
表1 仿真参数
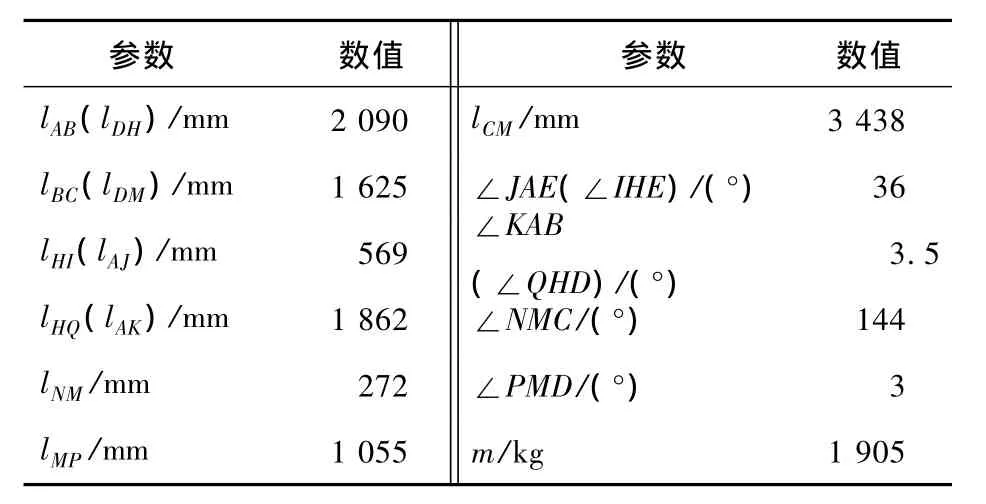
表2 折臂式门架主要尺寸参数
4.2 仿真及结果分析
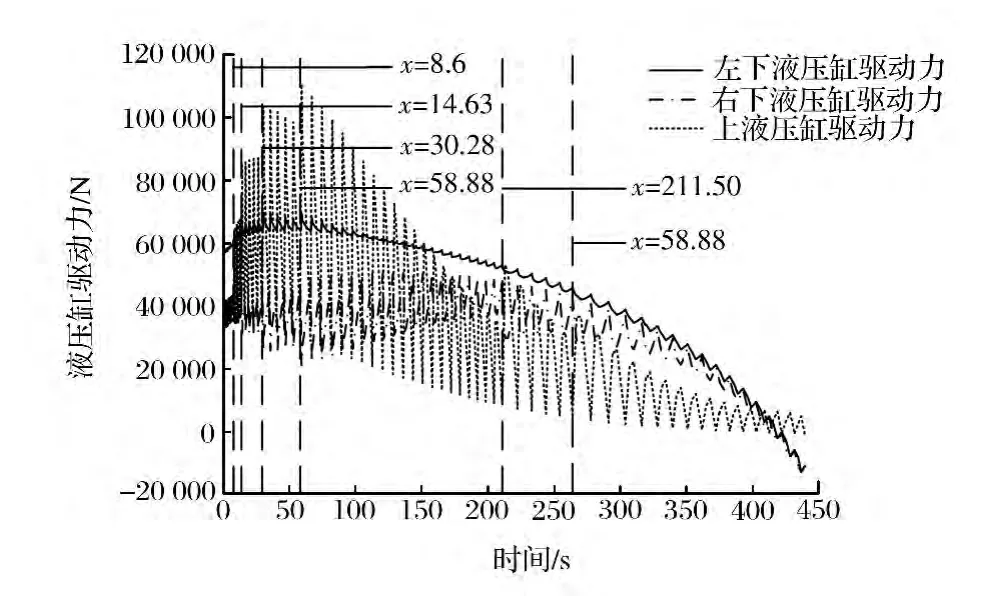
图5 展开过程中液压缸驱动力变化曲线
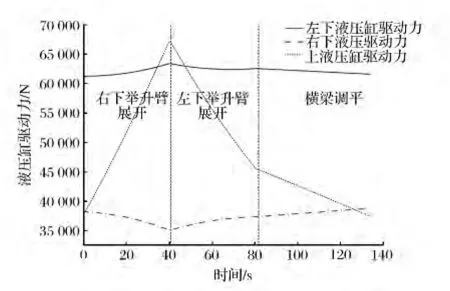
图6 展开子过程中液压缸驱动力变化曲线
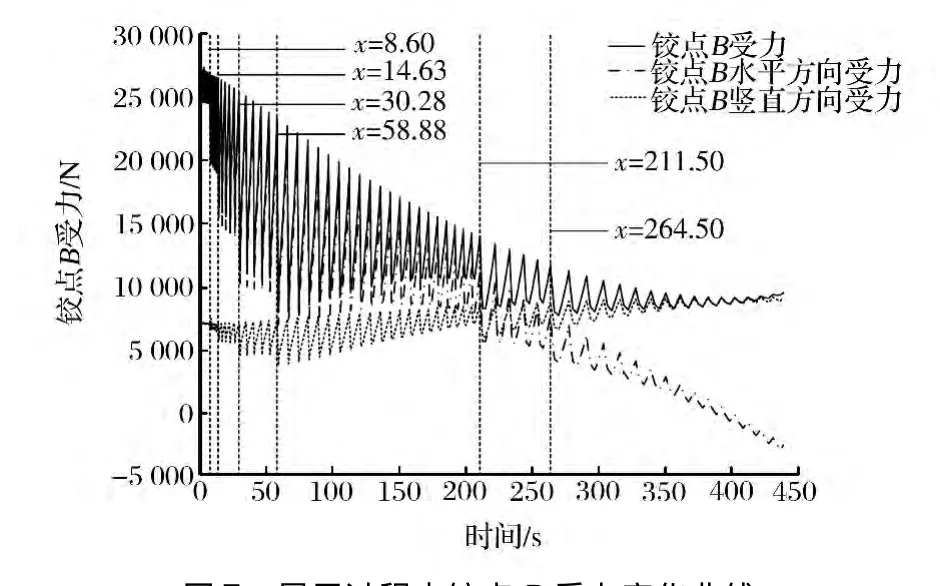
图7 展开过程中铰点B受力变化曲线
应用Matlab软件编程并进行仿真[3],得到仿真结果(如图5—8所示)。分析图5—8可以发现,液压缸驱动力和铰点受力随门架的展开逐渐减小,在每个展开过程中液压缸驱动力和铰点受力都呈震荡变化,其振幅主要由举升臂的展开幅度和门架的展开阶段决定:当举升臂的展开幅度保持不变时,随着门架的不断展开,液压缸驱动力和铰点受力振幅不断减小;当门架所处展开阶段相同时,举升臂展开幅度越大,液压缸驱动力和铰点受力振幅越大。
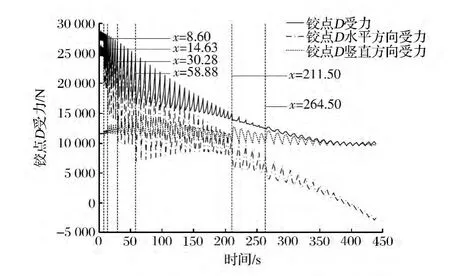
图8 展开过程中铰点D受力变化曲线
5 结语
本文提出了一种新型折臂式门架结构,运用坐标变化矩阵法对门架的展开过程进行了数学分析,并利用Matlab软件进行了仿真。根据仿真结果可知,在制订门架展开作业方案时应注意以下两点:在展开过程的初始阶段,门架每次的展开幅度应尽可能小;随着门架的不断展开,可以逐渐增大门架每次的展开幅度,但也不宜过大。
[1] 李海波.轻型集装箱跨运车的开发及应用[J].港口装卸,2009,1(1):1-4.
[2] 詹隽青.军用特种车辆设计[M].北京:国防工业出版社,2003:25-30.
[3] 张正兵,陈进,李晓娜.基于正铲液压挖掘机挖掘轨迹的机构运动学分析[J].机械,2008,35(5):9-12.
[4] 田方,范智广,邵娟.滑片压缩机的Matlab动力学模拟分析[J].压缩机技术,2005,191(3):13-15.
