基于分层总和法的水泥搅拌桩复合地基沉降分析

2015-05-06魏士淇杨晓蓉周永波

军事交通学院学报 2015年4期

魏士淇，杨晓蓉，周永波

(1.71872部队，河南信阳464000;2.军事交通学院基础部，天津300161)

根据复合地基理论，水泥搅拌桩复合地基可以视为一双层地基，由加固区和下卧层组成。其沉降包括加固区的沉降和桩端下未处理区的沉降。目前，对于复合地基沉降的计算主要基于分层总和法:加固区沉降常采用复合模量法、桩身压缩量法或应力修正法进行计算;下卧层沉降常采用的方法主要有压力扩散法、等效实体法和改进Geddes法等［1－3］。本文基于复合地基理论的分层总和法，确定加固区和下卧层沉降的计算方法，定量地分析各因素对沉降计算结果的影响，为获得滨海新区复合地基沉降计算的有效方法提供理论支撑。

1 计算方法分析

1.1 加固区沉降S1

应力修正法没有考虑桩土间的相互作用，且忽略了桩体的存在，导致使用该方法计算的复合地基加固区沉降值往往较实测沉降偏大。在计算应力修正系数的过程中需要确定桩土应力比，但由于影响桩土应力比的因素较多，很难对其进行合理取值。

使用桩身压缩量法计算复合地基加固区沉降时，不仅要考虑桩土应力比，还需要对桩侧摩阻力的分布进行确定。而桩侧摩阻力的分布形式仍是一个需要进一步研究的课题，目前很难进行合理选取。且由于桩体刺入下卧层的刺入量需要通过工程经验估算，也会对计算结果产生较大影响。一般认为桩身压缩量法适用于桩端有较好持力层，桩体不发生进入下卧层的刺入沉降或该刺入沉降很小的情况。而滨海新区地下软土层深厚，实际工程中桩体不可避免地会穿透加固区刺入到下卧软土层。因此，桩身模量法不适用于该地区沉降计算。

复合模量法具有概念明确、计算方便的优点，使用该方法计算时影响因素较少，在工程实践中被广泛应用，因此，本文选用复合模量法进行复合地基加固区沉降计算。复合模量法考虑到水泥搅拌桩对软土地基的改良作用，按照桩土协调变形的假定将复合地基加固区中的桩体和土体看为一个整体，采用统一的复合压缩模量［4－5］。

1.2 下卧层沉降S2

在复合地基下卧层沉降的计算方法中，利用等效实体法计算时，合理地选取桩侧摩阻力是一个较难解决的问题。作为一个分离体，加固体两侧的剪应力分布十分复杂，桩侧摩阻力实际上为一种近似概念，因此利用等效实体法计算复合地基下卧层沉降误差较大。采用改进Geddes法计算时，一方面需要通过计算桩土应力比而求得载荷分担比，另一方面需要对桩侧摩阻力的分布进行假设，容易造成误差的因素较多，其计算精度也很难得到保证。相比而言，压力扩散法计算简单，且计算过程中对计算结果的影响因素较少，因此本文选用该方法进行复合地基下卧层沉降计算。

2 水泥搅拌桩复合地基沉降计算

2.1 加固区沉降S1的计算

复合模量法计算加固区沉降S1的计算式为

式中:Δpi为加固区第i层复合土层的附加应力增量;Ecsi为加固区第i层土的复合模量;hi为加固区第i层土的厚度。

(1)计算 Δpi。

式中:σzi为第i层复合土层的上层面附加应力值，σz1=p0;σz(i+1)为第i层复合土层的下层面附加应力值。

公路路堤中心下荷载通常为矩形均布荷载，荷载密度为p0，将复合地基加固区分为n层，根据Boussinesq解得

式中:a为复合地基荷载作用宽度;b为复合地基荷载作用长度;z为加固区前i层土的总厚度，z=，i=2，3，…，n。

(2)计算 Ecsi。

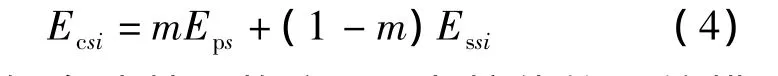
式中:m为复合地基置换率;Eps为桩体的压缩模量;Essi为第i层桩间土的压缩模量，由试验确定。

复合地基置换率为

式中:fspk为复合地基承载力特征值，由试验确定;Ra为单桩竖向承载力特征值，由试验确定;Ap为桩的横截面积;β为桩间土承载力折减系数。

2.2 下卧层沉降S2的计算

采用压力扩散法计算下卧层沉降S2(如图1所示)，其计算式为

图1 压力扩散法计算下卧层沉降S2

下卧层顶面土体上的荷载作用面为矩形，采用压力扩散法求得，载荷作用宽度a'=a+2h'tan θ，载荷作用长度 b'=b+2h'tan θ，h'为下卧层厚度，θ为压力扩散角。则下卧层土体顶面载荷密度为

对下卧层顶面土体，荷载密度为pb'，将复合地基加固区分为n'层，根据Boussinesq解得

合理地选取和确定压力扩散角θ是使用压力扩散法对下卧层上载荷进行准确计算的关键。对于复合地基，压力扩散角的取值与双层地基以及天然地基有所不同，根据文献［6 －7］，θ取 0.25 φ较为合理(φ为土体内摩擦角)。

3 复合地基沉降计算结果分析

3.1 桩体模量对复合地基沉降的影响

在其他影响因素不变的情况下，利用所编制的Matlab计算程序分别计算了桩体模量为100、200 MPa到1 000 MPa时水泥搅拌桩复合地基的沉降值，得到桩体模量对复合地基沉降计算结果的影响曲线(如图2所示)。

图2 桩体模量对复合地基沉降计算结果影响曲线

由图2可以看出，桩体模量的变化对复合地基沉降的计算结果有较大影响。随着桩体模量的增大，复合地基沉降计算值逐渐减小，且减小幅度逐渐降低，当桩体模量大于500 MPa时，复合地基沉降计算值几乎不再减小。这与实际工程经验吻合，进一步证明了在水泥搅拌桩复合地基中桩体模量并不是越大越好，在工程中为了避免浪费，应选择适当的桩体模量。

3.2 置换率对复合地基沉降的影响

在其他影响因素不变的情况下，分别计算了置换率为 0.05、0.10、0.15、0.20、0.25 和 0.30 时水泥搅拌桩复合地基的沉降值，得到置换率对复合地基沉降计算结果的影响曲线(如图3所示)。

图3 置换率对复合地基沉降计算结果影响曲线

由图3可以看出，置换率的取值对复合地基沉降计算结果有较大影响。当置换率小于0.2时，随着置换率的增大，复合地基沉降计算值降低幅度较大，当置换率大于0.2时，复合地基沉降计算值随着置换率降低的幅度逐渐减小并趋于稳定，此计算结果变化趋势符合实际工程经验所得的规律。

3.3 压力扩散角对复合地基沉降的影响

在其他影响因素不变的情况下，分别计算了压力扩散角为 5°、10°、15°、20°、25°和 30°时水泥搅拌桩复合地基的沉降值，得到压力扩散角对复合地基沉降计算结果的影响曲线(如图4所示)。

图4 压力扩散角对复合地基沉降计算结果影响曲线

由图4可以看出，复合地基沉降的计算结果随压力扩散角的增大而减小，且沉降计算值随压力扩散角变化的幅度较大。因此，在计算过程中，为了使计算结果尽可能与实际沉降吻合，压力扩散角应根据地区情况进行合理确定。

3.4 加固区厚度对复合地基沉降的影响

在其他影响因素不变的情况下，分别计算了加固区厚度为6、8、10、12、14 m 时水泥搅拌桩复合地基的沉降值，得到加固区厚度对复合地基沉降计算的影响曲线(如图5所示)。

图5 加固区厚度对复合地基沉降计算结果影响曲线

由图5可以看出，在计算深度相同的情况下，复合地基沉降计算的结果随加固区厚度的增大而呈现出不规则增大的趋势，而这种变化趋势与工程实际中复合地基沉降变形的规律并不相符。其原因是由于加固区与下卧层厚度发生变化，在使用分层总和法计算沉降的过程中对土体的分层情况也会随之作出相应的调整，这对沉降的计算结果产生了一定的影响。