我军陆路机动重装备运输性技战术指标分级
2015-05-06李遂汝刘锡鑫
李遂汝,刘锡鑫,肖 强
(1.军事交通学院国防交通系,天津30161;2.军事交通学院政治部,天津300161)
随着我国综合国力的不断增强,一大批重型武器装备陆续列装部队。这些重型武器装备在铁路、公路运输中普遍存在着超长、超重等超限问题,成为制约我军陆路机动效率的关键所在。通常为了解决超限装备的运输问题,主要有两种途径:一是对于极端超限的个别装备研究专门的保障装备;二是对于大多数且运输频率较高的重装备,按照其技战术指标对现有的交通基础设施和运载工具进行改建和改造。但是由于对我军主要陆路机动重装备的技战术指标缺乏系统的分析,实际工作中两种途径都存在着很大的盲目性。如对交通基础设施和运载工具进行改建和改造时,往往按照重装备技战术指标的最值进行“一刀切”,这样要么造成经济、军事和技术储备的浪费,要么导致改建和改造难以实现。因此,为增强我军交通运输保障的准确性,提高保障效率,本文从统计分析的角度出发,结合层次分析法的思想,对我军主要陆路机动重装备技战术指标的分级处理进行一定的探索。
1 分级原理分析
1.1 分级水平的确定
在以往针对交通基础设施改扩建和运载工具加装改造的分级研究中,通常划分为3个级别,如:我国交通重点目标按照一、二、三级进行划分;需要从军事重要性角度进行改扩建的桥梁划分为一、二、三级重点桥梁[1]。综合考虑改扩建和加装改造的需求,本文也将重装备技战术指标划分为3个级别水平,即:一级水平的技战术指标为极重要或经常使用的交通基础设施的改建和民用运载工具的改造提供参考;二级水平的技战术指标为一般重要或选择性使用的提供参考;三级水平的技战术指标为普通或不常用的提供参考。
由林德伯格-列维中心极限定律可知,对于服从同一分布且具有有限数学期望μ和方差σ2的一组相互独立的随机变量,当样本充分大时,样本均值近似服从均值为μ、方差为σ2的正态分布,即¯X~N(μ,σ2)。因此,若将重装备参与军事运输的过程看作以我军所有装备为总体进行的独立重复的取样试验,则所抽取装备技战术指标的均值服从正态分布。基于此,参考评价理论中对优良线和及格线的确定方法[2],以及概率统计理论中三方差定律对3个级别的统计学划分,在对我军主要重装备技战术指标进行统计分析后,可分别以μ、μ+σ和μ+2σ作为3个级别水平装备技战术指标的取值。对于一级水平,装备技战术指标的参考值为μ+2σ;对于二级水平,装备技战术指标的参考值为μ+σ;对于三级水平,装备技战术指标的参考值为μ。
1.2 层次分析及一致性检验
由于对重装备技战术指标进行的分级,应当同时考虑各装备技战术指标的大小、装备的列装数量以及装备的运输频率,因此取样试验应依据我军重装备的运输资料进行。考虑到这样做缺乏可操作性,本文提出借鉴层次分析法中构造成对比较矩阵的思想,来估计各重装备被抽取到的比例。即不进行取样试验,而将通过层次分析法确定的各装备的数量权重作为取样试验中各装备被抽取到的比例。
运用层次分析中构造成对比较矩阵的方法来估计重装备在运输中出现的比例,应当进行一致性检验。而在一致性检验时,要使用平均随机一致性指标(RI)参与计算。通常对于阶数不大于15的低阶成对比较矩阵,其平均随机一致性指标可查表获得。但对于高阶成对比较矩阵的平均随机一致性指标无法直接获取。而对于重装备的抽取试验,同一类别内装备的数量往往要大于15。本文按文献[3]中的方法,给出将用到的高阶平均随机一致性指标(见表1)。

表1 高阶平均随机一致性指标(RI)值
1.3 计算示例
一般来说,涉及军交运输保障的重装备技战术指标主要包括装备的长宽高尺寸、转弯半径、装备质量和装备爬坡能力几个方面,这里以装备的长度尺寸说明计算原理。以我军所有武器装备为总体,进行n次相互独立的装备取出试验,设第k次取出装备的长度为 Xk(k=1,2,…,n),则可知Xk为满足相同概率密度分布的随机变量。记多次取出试验的平均值为 ¯X,期望为 E(Xk)= ¯X= μ,方差为 D(Xk)=σ2。
设取样试验中第k件装备的长度尺寸为xk(k=1,2,…,n);依据装备的列装数量和运输频率对其进行的权重评分为ck,表示第k件装备在运输中出现的平均比例。据此确定的归一化权重ωk为

期望为
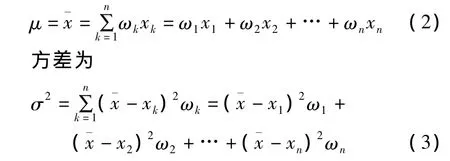
如1.1所述,对于一级水平,装备长度尺寸的参考值为μ+2σ;对于二级水平,装备长度尺寸参考值为μ+σ;对于三级水平,装备长度尺寸参考值为μ。运用同样的方法可分别求得装备宽度尺寸、高度尺寸、转弯半径、质量和爬坡能力几个技战术指标各级别的取值,其中爬坡能力相对其他指标为负向指标,分别取μ-2σ、μ-σ和μ作为各级别的取值。
2 计算过程
通过对我军主要重型武器装备的技战术指标进行统计,分析了9大类共110种装备的技战术指标数据,9类装备分别为地地导弹、防空导弹、坦克、装甲车、防空高炮、野战炮、工程装备、防化装备和情报雷达,给出3个级别水平的装备技战术指标值。
2.1 权重计算
通过层次分析法构造成对比较矩阵来计算各类权重,共涉及4类权重。
(1)组别权重。通过对9类装备进行两两比较,得到用于估计这9类装备数量的权重值,记为ak(k=1,2,…,9),组别权重按照表 2 的比较尺度进行的取值。

表2 装备数量比较尺度对照
(2)装备组内权重。对同一组别的装备进行两两比较,得到用于估计该组内各型装备数量的权重值,记为bkj(k=1,2,…,9;j的取值取决于组别)。
(3)装备组合权重。用于整体估计所有列出重型装备数量的权重值,为组内权重和组合权重的乘积。设第k组共有dk型装备,装备组合权重记为ci。对于第m组第n型装备:

(4)归一化权重。将装备组合权重去除指标值为空的对应项后进行归一化处理所得的权重值。设装备总型号为n型,第i型装备的某项指标的数值为xi,归一化权重记为ωi:

式中当xi=0时,ci=0。
2.2 一致性检验
对确定组内权重和组别权重的10个成对比较矩阵进行一致性检验可知,10个成对比较矩阵均满足一致性。检验结果见表3。
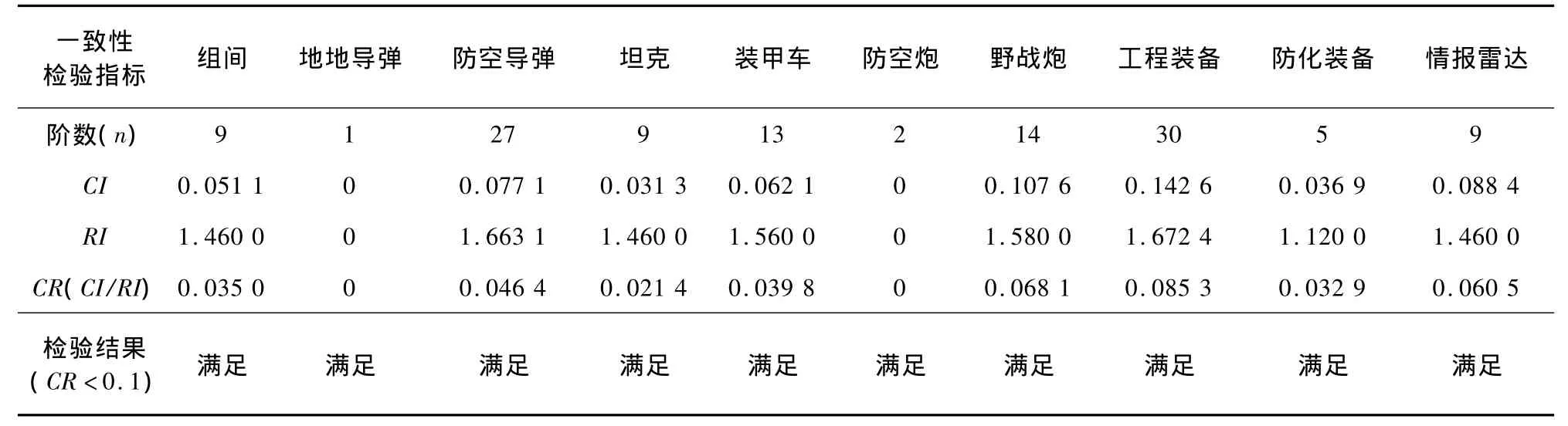
表3 一致性检验结果
2.3 计算结果
装备技战术指标计算结果见表4,限于篇幅仅 列出部分计算数据。

表4 装备技战术指标计算结果汇总
如前所述,以μ+2δ、μ+δ和μ作为3个级别水平装备技战术指标的取值。将以上分析结果进行汇总,见表5。这样,在今后涉及陆路机动重装备运输性具体问题的分级研究中,便可以按照表5中运输性技战术指标的统计数值进行选取使用。
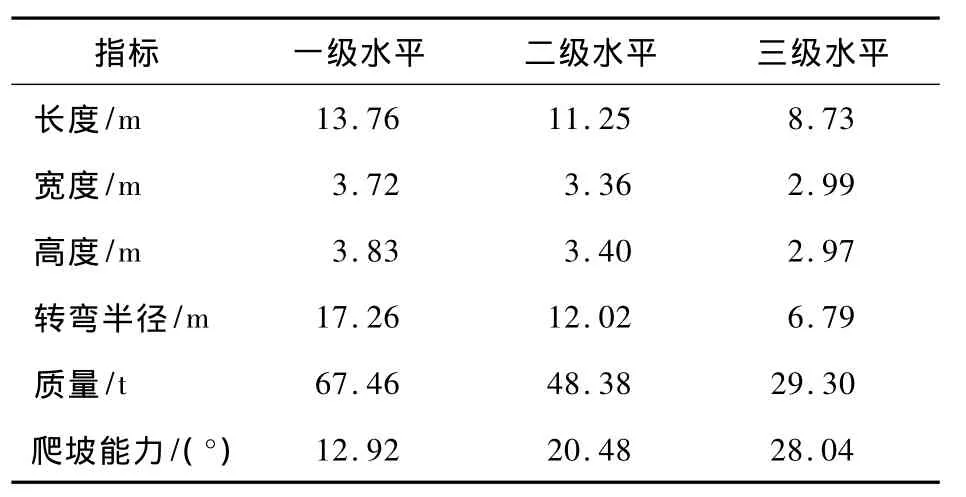
表5 技术标准等级参照技战术指标汇总
3 结语
对我军主要陆路机动重装备技战术指标进行分级处理,是提高我军军交运输保障准确性的必然要求。通过本文的研究,初步探索了一种计算不同级别重装备技战术指标数值的方法,并给出了具体的结果。但是这一方法仍然存在着一定的局限性。为了进一步提高各级别所给出数值的准确性和可参考性,还有待对这一问题进行深入的研究探索。
[1] 徐理博,常春伟,李遂汝,等.对铁路桥梁建设贯彻国防要求有关问题的探讨[J].国防交通工程与技术,2012(6):4-7.
[2] 王雪青,赵辉.执业资格考试及格线确定的方法探讨[J].东南大学学报:哲学社会科学版,2007(3):50-52.
[3] 洪志国,李焱,范植华,等.层次分析法中高阶平均随机一致性指标(RI)的计算[J].计算机工程与应用,2012(12):45 -47,150.
