一种基于迭代交织的任意长度扩频码生成器

朱建锋，安建平，王爱华

(北京理工大学 信息与电子学院，北京 100081)

一种基于迭代交织的任意长度扩频码生成器

朱建锋，安建平，王爱华

(北京理工大学 信息与电子学院，北京 100081)

扩频码设计是北斗系统信号体制的重要内容，同时满足码长选择灵活性和良好性能是扩频码设计中的难题，自主知识产权也是北斗信号设计的目标之一。基于交织运算和反馈-迭代结构提出一种适合任意长度的扩频码生成器，利用交织运算的随机化效应产生随机序列，通过反馈-迭代运算产生扩频码候选集合，讨论了交织运算器和种子序列的选择准则。采用迭代交织生成器构造1 023、2 046、4 092、10 230比特扩频码方案，评估结果表明，迭代交织扩频码与全球定位系统、欧洲伽利略系统和中国北斗卫星导航系统的扩频码方案相比性能相当或更优。迭代交织生成器可以生成任意长度、性能良好的扩频码方案，同时具有完美平衡性和计算复杂度低的优势，为我国北斗系统信号设计提供了一种候选方案。

扩频码生成器；迭代交织；任意码长；交织运算器

扩频码是任何基于扩频通信体制的无线通信、测量系统信号体制设计所必需的，扩频码的码长、码相关性是影响信号抗干扰能力、多址能力和测量精度的重要因素[1]。移位寄存器法、数论法和计算机搜索法是三种主要的卫星导航信号扩频码构造方法，线性移位寄存器法(linear feedback shift register，LFSR)的优势是码相关性好、生成计算复杂度低[2]，但码长受生成多项式周期制约；全球定位系统(global positioning system，GPS)L1C信号的Weil码是基于数论方法设计的[3]，Weil码显著改善了码自相关性能，设计Weil码的前提是在码长附近找到一个生成素数；欧洲伽利略系统(Galileo navigation satellite system，Galileo)的E1 OS信号扩频码使用遗传算法通过计算机搜索实现[4]，计算机搜索可以得到一些有特色的码字如零自相关旁瓣(autocorrelation side lobe zero，ASZ)，但是由于计算复杂度的限制只能用于较短的码长如4 092、5 115比特。可以看出，现有的扩频码构造方法都不能满足灵活选择码长的要求，而码长灵活性是卫星导航和扩频通信信号体制设计者所期望的，一种适合任意码长、性能良好、低复杂度的扩频码构造方法将极大地降低信号体制设计中平衡信号频谱带宽、信息速率和用户数量的难度。

本文提出一种适合任意码长、低复杂度的通用扩频码生成器，首次将迭代交织运算应用于扩频码构造。分析了交织运算的数学模型和随机化效应，提出扩频码构造的迭代交织系统模型，扩频码生成只包含线性复杂度的位置交换运算。使用通用生成器设计4种不同码长的扩频码，与现有11种不同生成方法、不同码长的导航信号扩频码评估和对比表明：在主要性能测度上迭代交织码(iterative interleaving code，IIC)与GPS、Galileo和我国北斗卫星导航系统(BeiDou navigation satellite system，BDS)扩频码相当或更优。迭代交织还能够满足BDS对自主知识产权的要求，为BDS信号体制设计提供一种候选方案。

1 迭代交织运算的数学模型

1.1 交织运算的两种模型

交织运算的最初目的是为了提高突发错误信道中的纠错能力[5]，通过位置置换可以将连续的突发错误转换为随机错误。在以误码率为测度的场景下，对于交织运算器的建模和研究侧重于周期性、因果性、延时和内存占用[6-7]，典型的交织器包括分组交织器和卷积交织器，本文中应用的交织器限定于分组交织器。分组交织器包含3个要素：交织序列s={si}、输入序列u={ui}、输出序列v={vi}，i=1,2,...,N，N为序列长度，交织的数学含义是从u到v的一一映射，s则表示映射的实现方式，即

v=f(u,s)

(1)

交织器可以用位置置换和矩阵乘法两种数学工具来分析。在位置置换模型中，交织序列s是正整数1，2，…，N的一个排列，交织器的输入和输出关系为

(2)

在矩阵乘法模型中，序列u、v、s可以用矢量U、V和矩阵S表示，其中U(i)=ui，V(i)=vi，1≤i≤N，交织矩阵S的元素为

(3)

其中1≤i≤N，1≤j≤N。则交织过程可以表示为矩阵乘积形式

V=U×S=US

(4)

比较两种模型，矩阵乘法模型形式清晰简洁，但实现复杂度为O(N2)，位置置换模型的物理意义清晰，实现复杂度为O(N)，更适合交织运算的工程实现。

1.2 随机化效应和迭代交织模型

文献[5]最早提出了交织运算的随机化效应，指出随机化效应是实现将突发错误转化为随机错误的关键，并以错误模式的概率分布作为随机化测度。在早期以误码率为目标的应用中，考虑到交织和解交织的延时和存储空间，这一阶段以规则交织器为主。在提出近香农限的Turbo码以后，交织器成为影响Turbo码性能的关键因素之一，非规则、分组交织研究成为热点，面向Turbo码的交织器设计遵循两项原则：长交织器和输出序列尽可能随机化[8]，随机化效应是利用交织运算构造随机扩频码的基础。

迭代交织系统模型的提出借鉴了纠错译码中的迭代译码思想(图1)，系统由输入序列、交织器和反馈回路组成，第一次使用的输入序列也称为种子序列，交织器则由交织序列描述，交织器的输出通过反馈回路返回输入端作为下一迭代的输入序列。基于迭代交织结构模型，多次迭代可以产生多个输出序列，这些输出序列构成了扩频码设计的候选集合。

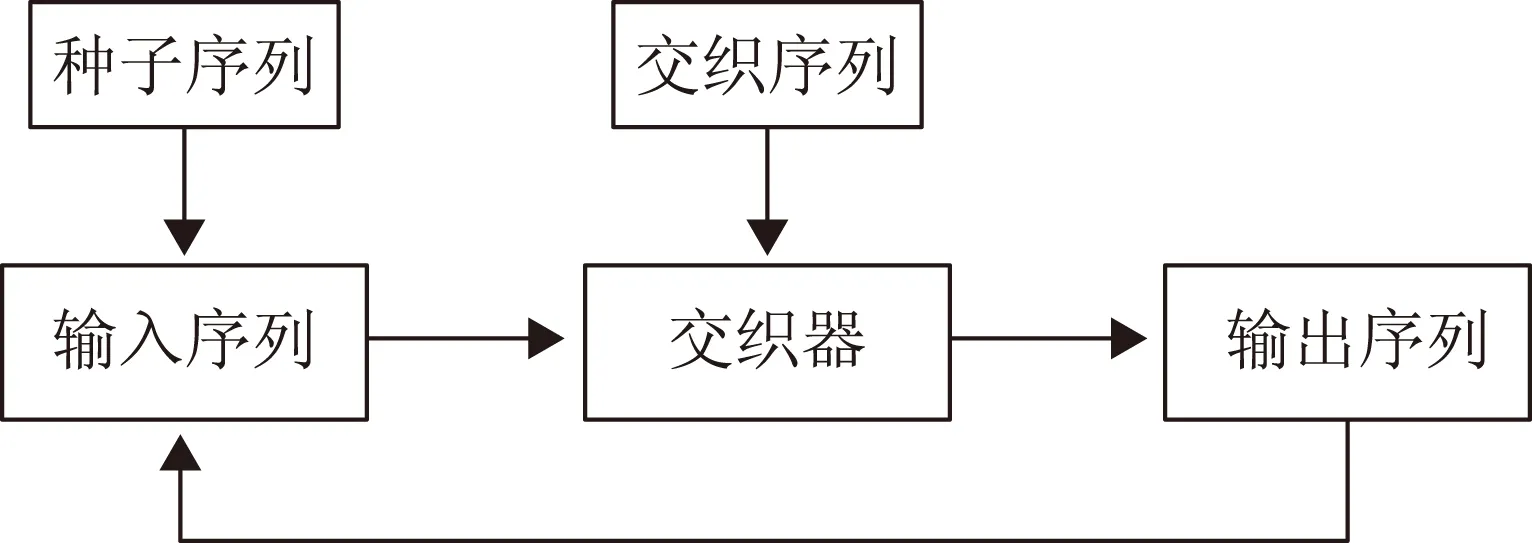
图1 迭代交织系统模型

以矩阵乘法模型作为工具分析迭代交织运算，第一次迭代的输入序列U=U0，交织矩阵为S，第k次迭代的输出序列为Vk，则有

(5)

迭代交织运算的实质是种子序列和交织矩阵的k次乘方的乘积，因此输出序列Vk决定于三个因素：种子序列U0、交织矩阵S和迭代次数。

2 基于迭代交织的扩频码构造

基于迭代交织结构模型，通过若干次迭代交织可以生成扩频码的候选集合。交织矩阵和种子序列是产生具有良好性能扩频码的关键要素，二者需要进行优选，优选的目的是(1)产生具有期望特征的扩频码；(2)防止迭代交织结构进入病态。

2.1 交织器的选择

交织器的选择包括两个问题：(1)选择何种交织器；(2)交织序列的长度能否任意选择。Turbo码出现后，为优化Turbo码性能对交织器进行了大量研究工作[9]，出现了规则交织器和非规则交织器两大类的多种交织器方案，其中非规则交织器具有较好的交织增益。虽然可选的交织器结构非常多，但是并非都可以用于构造扩频码，某些类型的交织器会导致迭代过程进入病态。例如自反交织器[10]，其设计目的是交织器和解交织器使用相同的交织序列以降低实现资源，其矩阵表示为S-1=S，那么S2n=E，采用这种交织器的迭代输出为：

(6)

其结果是迭代交织结构无法生成随机的输出序列，迭代交织结构处于病态，用于迭代交织的交织器需要进行自反性检验。

在使用迭代交织构造扩频码的过程中，输出序列的随机性是选择交织器最重要的测度。在不同的交织器结构中，随机交织器和S随机交织器具有良好的随机化效应。特别是S随机交织器，输入序列中的相邻符号交织后的距离至少为

为交织序列长度，本文选择S交织器作为构造扩频码的交织器。对于第二个问题，文献[12]提出了构造任意长度S交织器的方法。

2.2 种子序列构造

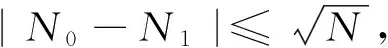
在基于迭代交织的扩频码构造方法中，通过对种子序列的控制可以实现完美平衡性。由于在迭代交织运算中，输出序列的01个数保持不变，因此只要种子序列U0的满足完美平衡的条件，那么所有迭代交织后的序列都满足完美平衡性。生成具有完美平衡性的种子序列可以采用两种策略：(1)筛选法，任意生成01序列，拒绝所有不满足01完美平衡性的序列，直至获得一个满足完美平衡性的序列；(2)规则构造法，按照某种规则构造01完美平衡性的序列，一种可行方案是采用0、1交替构造种子序列。

2.3 实现步骤

基于迭代交织方案构造扩频码的步骤如下，输入条件为扩频码长度N，扩频码候选集合元素数M，种子序列为U0，交织序列为S，交织器为S随机交织器，交织器通过自反性检验，生成过程采用矩阵表示。

步骤1.参数初始化。

采用规则构造方法种子序列U0，其中

(7)

将种子序列赋予输入序列U=U0，迭代计数器k=1。

步骤2.交织生成扩频码。

输入序列U通过交织器S产生输出序列Vk，即

Vk=US

(8)

保存为扩频候选集合中的第k个元素，Vk反馈回输入端作为下一次的输入序列U=Vk。

步骤3.迭代交织。

检查迭代计数器，如果k=M停止迭代，否则计数器加1，返回步骤2进行下一次迭代。

至此，候选扩频码中已经包含M个长度为N的扩频码序列，候选集合中码序列是进行后续扩频码设计工作的基础。

3 性能仿真与分析

为验证使用迭代交织生成器生成扩频码的性能和复杂度，以GPS、Galileo和BDS的接口控制文件(interfacecontroldocument，ICD)中的扩频码作为比较对象，共选择不同生成方法、不同的码长的扩频码方案11种，码长包括1 023、2 046、4 092、10 230比特，生成方法包括Gold序列、截断m序列、Weil码、随机存储码等。使用迭代交织生成器构造4组同样码长的扩频码方案(IIC-1203、IIC-2046、IIC-4092、IIC-10230)，比较的性能测度包括：01个数差、偶自相关、奇自相关、偶互相关、奇自相关，性能比较如表1所示。

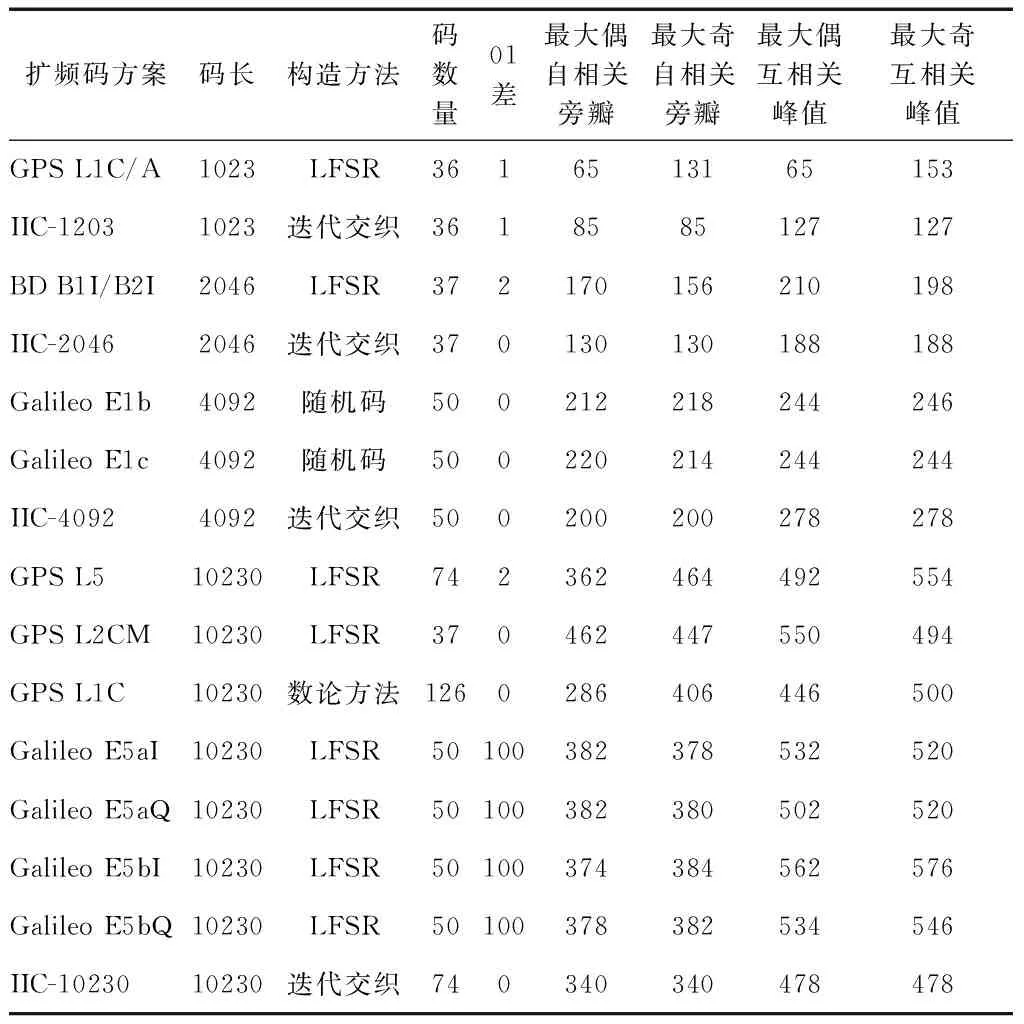
表1 扩频码性能比较

综合分析表1中的扩频码方案和性能测度可知：

(1)迭代交织扩频码在所有长度上具有完美01平衡性；

(2)迭代交织扩频码具有良好的自相关性，奇偶自相关性能比较平衡，GPS L1C/A、L1C扩频码具有偶自相关优势，但奇自相关没有优势；

(3)迭代交织扩频码具有良好的互相关性，奇偶互相关性能比较平衡，GPS L1C/A、L1C、Galileo E1信号具有互相关优势，但优势不显著；

上述迭代交织扩频码生成使用Matlab语言编程实现，在个人计算机(person computer，PC)上的构造时间从20 s至2 h不等。如果增加迭代次数可以进一步改善自相关和互相关性能。当前实验中使用的固定交织器并非必要条件，交织器动态更新也不存在技术障碍。

4 结束语

BDS的成功需要具有自主知识产权、高性能的信号体制方案，本文提出的迭代交织码可以同时满足灵活选择码长和性能良好的要求。以GPS、Galileo和BDS系统ICD中11种不同构造方法、不同码长的扩频码为对象进行性能评估和比较，迭代交织码在主要性能测度上与现有ICD方案相比相当或更优，迭代交织码为BDS信号体制设计提供了一种候选方案。基于迭代交织的扩频码生成器不仅适用于卫星导航系统，而且可用于任意使用二进制序列作为扩频码的无线扩频通信、测量系统。

[1] ZEPERNICK H J，FINGER A.Pseudo Random Signal Processing Theory and Application[M].Chichester：John Wiley & Sons Ltd，2005：225-227.

[2] IS-GPS-200F，Navstar GPS Space Segment/Navigation User Interfaces[S].

[3] IS-GPS-800B，Navstar GPS Spaces Segment/User Segment L1C Interfaces[S].

[4] OS SIS ICD Issue 1，European GNSS(Galileo)Open Service Signal In Space Interface Control Document[S].

[5] BRAYER K，CARDINALE O.Evaluation of Error Correction Block Encoding for High-speed HF Data[J].IEEE Transactions on Communication Technology，1967，15(3)：371-382.

[6] ANDREWS K，HEEGARD C，KOZEN D.A Theory of Interleavers[EB/OL].[2014-09-21].www.cs.cornell.edu/～kozen/papers/interl.pdf.

[7] GARELLO R，MONTORSI G，BENEDETTO S，et al.Interleaver Properties and Their Applications to the Trellis Complexity Analysis of Turbo Codes[J].IEEE Transactions on Communication Technology，1967，15(3)：371-382.

[8] BERROU C，GLAVIEUX A.Near Optimum Error Correcting Coding and Decoding：Turbo-Codes[J]. IEEE Transactions on Communication Technology，1996，44(10)：1261-1271.

[9] ANDREWS K.Turbo Codes and Interleaver Design[D].New York：Cornell University，1999.

[10] HO M S C，PIETROBON S S，GILES T.Interleavers for Punctured Turbo Codes[C]//Proceedings of IEEE Asia-Pacific Conference on Communications.Singapore：IEEE，1998：520-524.

[11] DOLINAR S，DIVSALAR D.Weight Distributions for Turbo Codes Using Random and Nonrandom Permutation：TDA Progress Report 42-122s[R].Pasadena，California：Jet Propulsion Laboratory Pasadena California，1995.

[12] LI Xiao-wen，CHEN Zhen-dong.A Design of Improved Flexible-length S-random Interleaver[C]//Proceedings of the 3rd International Conference on Computer Research and Development(ICCRD).Shanghai：IEEE，2011：391-394.

[13] MENEZES A J，OORSCHOT PC，VANSTONE S A.Handbook of Applied Cryptography[M].Boca Raton：CRC Press，1997：181-182.

A Flexible-Length Spreading Code Generator Based on Iterative Interleaving

ZHU Jian-feng，AN Jian-ping，WANG Ai-hua

(School of Information and Electronics，Beijing Institute of Technology，Beijing 100081，China)

Spreading code design is an important item of China BDS signal structure.It is difficult to meet the requirements of flexible code length and good performance in spreading code design at the same time.Independent intellectual property right is another goal of BDS signal structure.A flexible-length spreading code generator based on interleaving operation and feedback-iterate structure is proposed in this paper.Random sequence is build by the random effect of interleaving operation.The output sequences of iterative operations forms the candidate set of spreading codes.The critical of interleaving operator and seed sequence selection are discussed also.Four spreading codes families with 1023，2046，4092，10230 bits length are designed by using iterative interleaving generator.The result of evaluation shows that the performance of new code families is equivalent or better than spreading codes of GPS，Galileo and BDS.The new generator can used to design spreading codes with flexible code length and good performance.The iterative interleaving code has the benefit of perfect code balance，low generation complexity and provides a candidate for BDS signal design.

spreading code generator；iterative interleaving；flexible code length；interleaving operator

2014-10-14

国家高技术研究(863)发展计划(2011AA120502)。

朱建锋(1977)，男，河南封丘县人，博士生，研究方向为卫星导航信号设计与评估理论。

P

A

2095-4999(2015)-01-0023-04