基于FEM-SPH 耦合算法的船舶破冰数值模拟

胡 昕，詹成胜

(武汉理工大学，湖北武汉430063)

0 引言

随着极地航线的开辟，对冰区船舶与海冰的相互作用进行研究变得十分必要。冰排是面积足够大的漂浮冰体，通常是大面积的冰层，要想通过冰区水域必须与冰层发生挤撞［1］。国内外的研究热点主要在冰排与海工结构物如防波堤、闸墩、海洋平台桩腿的相互作用等［2—3］方面。目前学者们对于船舶与冰山、块状冰体或者冰排碰撞［1，4—6］结构响应研究的比较多，直接考虑船冰水三者耦合作用模拟船舶破冰过程的研究很少。因此，研究船舶与冰、水耦合系统作用具有重要的理论意义与实际工程价值，可以为冰区航行船舶的抗冰冲击强度分析提供依据。

由于传统的有限元方法在涉及流固耦合问题时遇到很多的困难，而FEM-SPH(有限元法-光滑质点流体动力学)耦合算法可以作为一种求解复杂流固耦合问题的新思路，它克服了因传统有限元网格严重畸变而引起的数值计算困难。本文以在层冰中破冰航行的KVLCC2船型为数值模拟对象，用光滑质点流体动力学这种无网格法模拟水，从而可以实现流体和固体系统的动态耦合分析。用合适的有限元网格模拟层冰，赋予冰适当的材料属性，软件可以模拟层冰的具体破坏形式以及破坏的动态过程。

1 算法简介

1.1 SPH 算法

1977年Lucyt和Gingold等分别提出了光滑质点流体动力学(Smoothed Particle Hydrodynamics，SPH)方法，并且成功应用于天体物理领域中。近年来该方法被广泛应用于处理结构动力学问题，主要是用于结构大变形解体、碎裂等分析(如高速碰撞、流固耦合碰撞等)［7］。

SPH基本思想是用一系列粒子表示问题域，用积分表示法来近似场函数，基于当前支持域分布的粒子，在每一时步通过粒子近似求解场函数及其导数，将粒子近似法应用于所有的场函数相关项中，得到只与时间相关的离散化形式，最后可以进行显式积分求解。这些使得SPH方法具有无网格、自适应、稳定以及拉格朗日性质。

函数核近似式、函数导数核近似式:

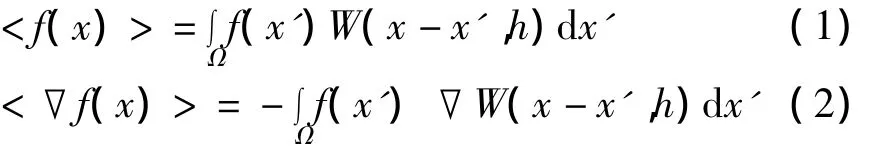
在粒子i处函数粒子近似式、函数导数粒子近似式:

式中:▽为梯度算子;W(x-x'，h)为光滑核函数，h为光滑长度，用来定义光滑核函数的影响区域;mj、ρj(j=1，2，...，N)为粒子j的质量和密度，N 为粒子j支持域内的粒子总数。

利用上面的粒子近似式可以将流体质量、动量和能量控制方程离散为下面的近似式:

式中:dρi/dt、dUi/dt、dEi/dt分别为粒子 i相应的随体导数。

当粒子i周围2倍光滑长度h内的粒子分布比较均匀时，用粒子近似式计算可以得到相当好的结果［8］。

1.2FEM-SPH耦合算法

FEM-SPH耦合算法实质是一种接触(自我接触、点面接触、面面接触等)算法。当SPH粒子与有限单元节点之间间距超过接触厚度(人工变量)时，将会在接触界面之间产生穿透，此时SPH粒子和有限元节点之间将会有接触力作用。任何位于有限元节点支持域内的SPH粒子都会对该节点产生接触力，反之任何位于SPH粒子支持域内的有限元节点也都会对该粒子产生接触力。

界面穿透量为Penetration，接触力FC大小可用式(8)、式(9)计算:

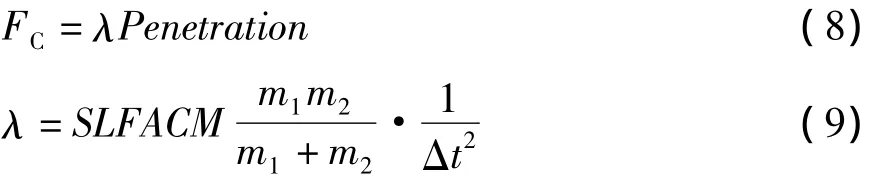
式中:SLFACM为接触力惩罚系数;Penetration为穿透厚度;Δt为时间步长;λ为接触刚度。

图1为接触穿透示意图，其中，Hcont为材料的接触厚度，为人工变量。

图1 接触穿透示意图

求出接触力后，将接触力以外力的形式加入到SPH动量方程和有限元动力学方程中［9］:

式中:M为结构质量矩阵;C为结构阻尼矩阵;K为结构刚度矩阵;F为外载荷矩阵;FC为接触力;Ü、U、d分别为某时刻的加速度、速度和位移。

SPH数值积分过程中采用变光滑长度的方法消除光滑长度改变造成的影响［10］。根据粒子之间接触力施加的原理(和光滑长度相关)，当界面之间没有穿透时，粒子节点之间就没有接触力，所以在计算过程中，不需要定义接触面以及接触面的法线方向。该算法对复杂接触面以及有限元网格变形较大的情况都适用。

2 数值模拟模型及参数

2.1 计算模型

本算例选用KVLCC2船型的缩尺(缩尺比为15.4)模型作为计算船体，模拟该船在层冰中连续破冰的工况。船模参数见表1。计算域模型和有限元网络、SPH模型如图2所示。

兼顾计算效率和计算结果，计算域范围设定为12 m×5 m×0.896 5 m。

表1 KVLCC2船模主尺度

图2 计算域模型和有限元网格、SPH模型

图2 (a)、(b)分别示意了计算域模型和网格模型，其中图2(a)示意了模型由船体、冰层、水(SPH粒子)、池壁边界4部分组成，池壁边界是一个没有顶面的空心长方体，水可以在池中自由运动，冰层恰在自由液面上且冰层与池壁接触的单元进行了全约束;图2(b)展示了遮蔽池壁后模型局部网格模型，船体网格为shell壳单元，数量为29 930，单元平均大小为0.017 75 mm;冰网格为solid实体单元，单元平均大小为0.017 75 mm，冰厚为38.9 mm，网格数量为328 192;水为SPH单元，数量为135 806，粒子的生成可以由六面体网格转化。

2.2 材料模型

冰力模型试验既具有液流模型试验的一切特点，同时也是一种材料力学特性的模型试验，因此根据冰力模型试验中的动力相似(重力相似、弹性力相似)可以导出试验中一些主要物理量的比尺。冰力模型试验物理量比尺见表2［11］。

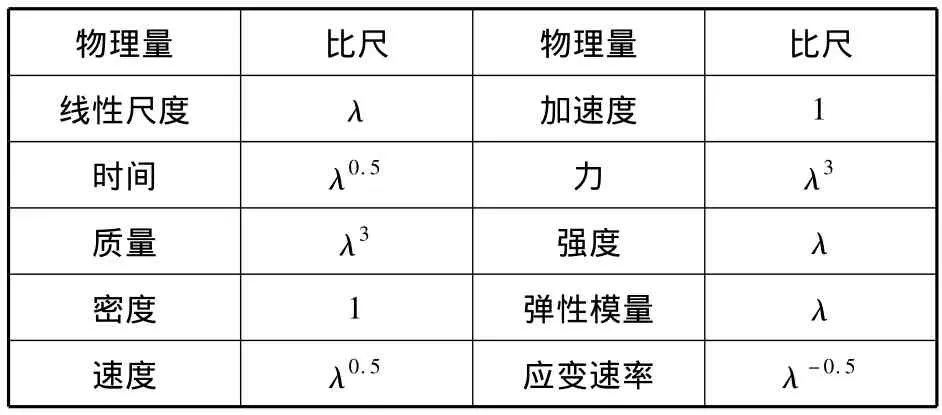
表2 冰力模型试验物理量比尺

根据以上比尺，可以计算得到缩尺模型所需要的冰材料属性参数。模型冰材料属性见表3。

表3 模型冰材料属性

冰的破坏随应变速率的不同表现为韧性破坏和脆性破坏，冰在高应变速率时的破坏表现为脆性破坏。本文计算中冰的应变速率远大于冰的韧脆破坏分界点的应变速率，因此采用高应变速率时的材料模型［12］。

本文数值模拟中，船体看作刚体模型，材料采用一般结构用钢;水体为SPH粒子，材料采用Murnaghan状态方程表示:

式中:P0为参考压力，P0=0;B为体积模量，B=27 300;ρ0为参照密度，ρ0=1 000 kg/m3;c为材料声速;ρ为流体计算密度;γ为指数系数，γ=7。

2.3 接触模型和模型约束

接触模型用来模拟计算模型中不同部分之间的相互作用，相互作用的面有主、从之分，主、从面之间不能有初始穿透。从属面的网格要比主面网格细密，防止主从穿透，因为穿透可能会引起沙漏现象的发生，后者导致计算出错。

本文计算中的接触模型定义有:船冰接触、船水接触、冰水接触、水池壁接触。上述接触模型中船冰接触，定义冰为从属面，其余定义水为从属面。接触力比例因子为人工变量，取为默认值0.1。接触深度为判断主从面之间是否接触的一个阀值，取值小于节点间距或者粒子间距，为人工变量，取值原则是要保证不能有初始穿透。

SPH单元属性设置中，核函数取为默认4阶贝塞尔核函数。软件中核函数光滑长度是变化的，变化范围一般取值为初始光滑长度的0.2～5倍。初始光滑长度和粒子半径有关。

本文计算中，对池壁单元和冰排最外围单元进行六自由度约束，对船舶进行垂向约束即不考虑船舶的升沉和纵倾。计算中也不考虑重力场的影响。刚性船舶经过0.1 s加速至1.401 m/s，然后匀速破冰前行。

3 数值模拟结果分析

为了和文献［13］中的数据作对比，除船舶主尺度外，文献中的主要参数经过换算后与本文计算一致。文献［13］中的船舶主尺度换算后的尺寸为(长×宽×吃水):5.517 2 m×1.168 m×0.422 m。

经过计算输出状态、求解器、程序版本、结束时间设置等，计算时间2 s，船舶受力稳定，结果收敛。其中航行方向的冰力时程曲线结果见图3，0.5 s后冰阻力稳定后平均值为180 N，文献［13］实验测得的船舶冰阻力换算后为225 N。由于二者船型、船宽和吃水不同，且KVLCC2船型没有做过冰区航行破冰试验，并不能确定本文计算结果的准确性，但是在冰力的量级上经过换算符合实测数据。本文计算船舶宽度小，计算得出的冰力极值小于实验值，佐证了结论:接触宽度的增大极大地影响着极值冰力的大小［14］。

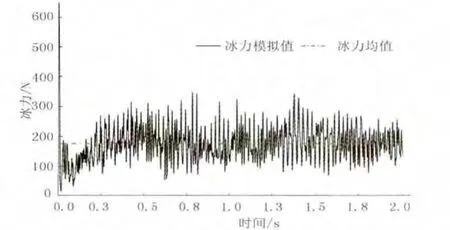
图3 冰力时程曲线

从图3可知，船冰刚开始接触时冰力最大超过了600 N，随着冰排的破裂，冰力迅速下降，最后在180 N上下波动，稳定后的冰力峰值接近400 N。图中冰力稳定后第1次峰值大约在0.8 s，第2次峰值接近1.4 s，因为这时有新的横向裂纹产生(见图4中④、⑧)。随着裂纹的扩展，处于裂纹线上的单元被删除，冰力时程曲线呈现规则波动，一旦裂纹扩展结束，要产生新的裂纹时，冰排在受到挤压过程中并没有单元被删除，此时冰力达到峰值。第3次峰值在1.6 s，由于前面初始裂纹的作用，此时的峰值明显小于前2次。

图4中各图显示了不同时刻冰排的动态断裂过程。冰排断裂过程中，在本文的船舶尺度和船速下冰排的断裂主要以弯曲断裂为主。通过删除失效的冰单元实现冰排的断裂，而冰单元的失效是由于裂纹尖端的应力集中，冰排局部Von Mises应力高达1.5×105Pa。

从图4可以知道:当冰排和船首接触时，船舶艏肩和艏部船舯最先出现裂纹并进行裂纹扩展，0.583 s船首两侧也出现了2道横向裂纹并扩展，接着在1.155 s船首部从边界斜(环)向宽度方向产生了2道裂纹把首部冰排分成了2个扇形的浮冰块，再往后还是产生类似的斜(环)向裂纹把扇形冰块儿后面的左右2块冰排切断。

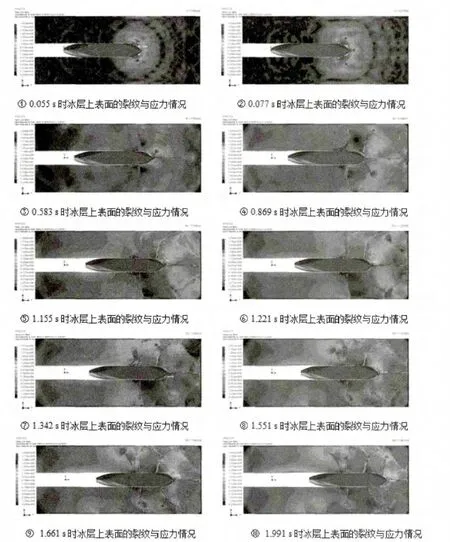
图4 海冰断裂动态过程

由于海冰断裂过程中裂纹尖端某些单元被删除，导致了冰排受力不均，使得裂纹现象并非完全对称，船舶两侧冰排也不是同时发生裂纹，呈现了一定的随机性。

一般来说，质量较好、均匀强度较高的海冰破碎周期呈正态分布，常见的破碎周期为3～4 s［15］。本文破冰周期取为从横向裂纹形成到扇形浮冰块儿形成的时间间隔，经过换算到实船尺度大约为3.2 s，与统计的最常见的海冰的破碎周期相符。

考虑船舶破冰工况下水的阻力变化这方面的资料较少，且缺乏实验数据，本文计算虽然直接用SPH粒子模拟了水的作用，但是其准确性还有待验证。图5给出了计算得出的水的阻力时程曲线，稳定后水阻力均值为80 N，根据经验此值偏大。由于本文对流固耦合计算采用的是接触碰撞算法，和传统CFD计算原理区别很大，所以水动力计算的准确性和专业CFD软件相比还有不小的差距。

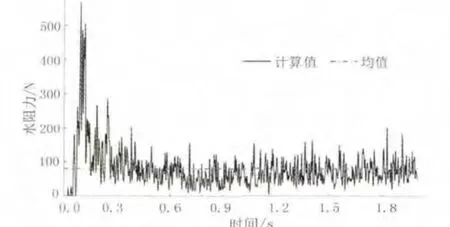
图5 水阻力时程曲线

4 结论

本文用SPH方法模拟水对船舶和冰排的作用，验证了SPH方法用于解决流固耦合问题是可行的。粒子之间的接触判断特别费时，因此在计算效率上还需要提升。

本文模拟了模型尺度下的船舶破冰过程，可以为模型试验提供参考。

文中数值模拟了海冰弯曲断裂过程，其冰力时程曲线与文献［13］中船舶冰力数据相符。在本文破冰速率下，冰排的破坏呈现脆性破坏。冰力时程曲线峰值对应于特定形式的裂纹(如本文中的横向裂纹)产生之前的一个过渡状态。

船型会影响流场及船艏兴波，进而对冰的破坏产生影响。文中船艏的形式并非破冰型艏，导致冰排向上弯折断裂。由于KVLCC2船型艏部干舷很小，部分冰块甚至冲上了甲板，因此合适的破冰型艏有利于破冰航行，更加有利于航行安全。

本文对KVLCC2船型破冰过程进行了数值模拟，对船舶的抗冰载荷结构设计和船舶冰区航行安全有一定的参考价值。

［1］ 张健，陈聪，张淼溶，等.船舶与冰排碰撞结构响应研究［J］.船舶工程，2014，36(6):24-26.

［2］ 路卫卫.冰排与建筑物挤压破坏有限元模拟分析研究［D］.天津:天津大学，2007.

［3］ 单思镝.河冰对桥墩撞击作用的数值模拟分析［D］.哈尔滨:东北林业大学，2011.

［4］ Daley C，Kim H.Ice collision forces considering structural deformation［C］//ASME 2010 29th International Conference on Ocean，Offshore and Arctic Engineering.American Society of Mechanical Engineers，2010:817-825.

［5］ Liu Zhenhui，Amdahl J，Loset S.Integrated Numerical Analysis of An Iceberg Collision With a Foreship Structure［J］.Marine Structures，2010(1):1-19.

［6］ 何伟.基于ANSYS/LS-DYNA的船舶与冰碰撞分析研究［D］.大连:大连海事大学，2013.

［7］ 张洪涛，赵美英，等.SPH和FEM耦合方法分析机翼前缘鸟撞的响应问题［J］.科学技术与工程，2009，9(7):1802-1806.

［8］ 徐志宏，汤文辉，罗永.光滑粒子模拟方法在超高速碰撞现象中的应用［J］.爆炸与冲击，2006，26(1):53-58.

［9］ 张志春，强洪夫，高巍然.SPH-FEM接触算法在冲击动力学数值计算中的应用［J］.固体力学学报，2011，32(3):319-324.

［10］ 强洪夫，高巍然.完全变光滑长度SPH法及其实现［J］.计算物理，2008，25(5):569-575.

［11］ 孙金亮.海上结构冰载荷的有限元分析和试验研究［D］.天津:天津大学，2007.

［12］ 张宿峰.流冰与桥墩的相互作用［D］.哈尔滨:东北林业大学，2014.

［13］ Su B，Riska K，Moan T.A numerical method for the prediction of ship performance in level ice［J］.Cold Regions Science and Technology，2010，60(3):177-188.

［14］ 韩雷，李锋，岳前进.冰-锥相互作用破坏全过程的有限元模拟［J］.中国海洋平台，2007，22(2):22-27.

［15］ 武文华，于佰杰，许宁，等.海冰与锥体抗冰结构动力作用的数值模拟［J］.工程力学，2008，25(11):192-196.

［16］ 张雄，刘岩.无网格法［M］.北京:清华大学出版社，2004.