基于DPCA和Radon变换的多通道SAR微动目标检测*

陈稳，张智军，秦占师，向建军，马赢

(空军工程大学 航空航天工程学院，陕西 西安 710038)

基于DPCA和Radon变换的多通道SAR微动目标检测*

陈稳，张智军，秦占师，向建军，马赢

(空军工程大学 航空航天工程学院，陕西 西安 710038)

为实现强杂波噪声条件下SAR微动目标检测，在DPCA信号的距离压缩域提出基于Radon变换和基于时频分析—逆Radon变换的2种微动目标检测方法。在距离压缩域，微动目标回波表现为沿方位向直线，利用Radon变换对直线的聚焦性实现微动目标检测；对DPCA信号作时频分析，微动目标引起的微多普勒频率表现为正弦形式，利用逆Radon变换对正弦曲线的聚焦性实现微动目标检测。通过对比，基于Radon变换的检测方法参数估计性能更好，而基于时频分析—逆Radon变换的检测方法具有更高的检测概率。最后，通过实验仿真验证了所提方法的有效性。

合成孔径雷达；微动目标; DPCA; Radon变换; 逆Radon变换

0 引言

目标或其组成部分除主体平动以外的振动、旋转等小幅运动称之为微动[1-2]。微动能反映目标精细运动状态，为雷达图像解译和目标识别提供了更加精细、稳定和可靠的依据。微动特征提取是当前目标探测与识别领域的热点，不仅可利用逆合成孔径雷达(inverse synthetic aperture radar，ISAR)成像技术对空间目标的微多普勒进行研究，也可利用合成孔径雷达(synthetic aparture radar，SAR)成像技术对地海面目标的微多普勒特征进行研究[3-4]。然而，大多数文献关注参数估计而非检测，而检测是识别的前提。

传统SAR-GMTI(ground moving target indication)技术难以检测微动目标。一方面，微动不能用低阶模型近似而不利于目标信息的长时间积累，使回波多普勒产生非线性调制；另一方面，SAR微动目标常淹没在强杂波中，微动使目标能量在多普勒域和图像域均发生分散[5]，不利于检测。已有相关文献对此问题进行研究：文献[6]利用时频分析技术提取振动目标多普勒信息，但没有解决交叉项抑制和提高时频分辨率间的矛盾；文献[7]根据目标微多普勒特征估计微动参数，但是未考虑强杂波噪声的影响；文献[8]利用数值模拟和实测数据研究了毫米波SAR体制下地面振动、旋转目标的微多普勒效应，但未给出性能稳健的检测方法；文献[9]采用自适应Chirplet变换和Hough变换提取微多普勒特征，实现低分辨雷达中微动多目标分辨，但未考虑杂波和噪声的影响，且时频分辨率低；文献[10]提出基于时频分析和杂波抑制的双通道SAR自旋目标检测方法，实现强杂波背景下的微动目标检测，但杂波对消技术没有消除噪声的影响。以上方法给SAR微动目标检测提供了技术支撑，但微动目标常淹没在强地杂波中，且传统的杂波对消技术无法消除系统噪声的影响。

本文模拟SAR振动目标的回波模型，采用相位中心偏执天线(displaced phase center antenna,DPCA)技术[11]对消杂波，在距离压缩域提出基于Radon变换[12-13]和基于时频分析—逆Radon变换2种微动目标检测方法，实现强杂波噪声条件下的振动目标检测。

1 双通道SAR回波模型

构造双通道机载SAR系统几何模型如图1。载机速度为va，高度为h，脉冲重复周期为T，天线间距为2d，采用单发双收模式。点目标P沿某轴振动，振幅为rm，振动角频率为ω，φ0为初相，振动中心Pnc的坐标为(xnc,-ync,0)。假设满足DPCA条件d=mvaT(m=1,2,3,…)，即两通道回波可完全配准。

图1 双通道SAR微动几何Fig.1 Geometrical model of multi-channel SAR-GMTI

令α0=π/2，α1=π/2(地距向振动)，β1=0，则t时刻前置天线与目标距离为

rmcos(ωt+φ0).

(1)

同理，t时刻等效虚拟天线与目标距离为

rmcos(ωt+φ0).

(2)

进行配准后的距离表示为

R2reg(t)=R2(t+mT)≈

rmcos[ω(t+mT)+φ0].

(3)

假设雷达发射带宽为Br、中心波长为λc的线性调频信号，则经过相干检波和距离压缩处理后，两通道接收信号为

(4)

式中：A0为常数，由天线双程方向图和目标后向散射系数决定。

沿距离压缩后得峰值，提取目标方位回波为

(5)

DPCA通过将配准后的两通道回波相减，使得静止地面背景被抑制。在原始数据域将两通道信号相消得

Δs(t)=s1(t)-s2(t)=

A0[exp(jφ1)-exp(jφ2)]=

(6)

代入式(1)，(2)，取模得目标DPCA信号幅度为

(7)

式(7)看出，由于静止目标的ω和rm均为0，于是Δs=0，表明静止目标回波信号被对消。而微动目标因为ω和rm均不为0，信号得以保留。对式(7)进行泰勒展开，考虑到|θ|≤10°时，sinθ≈θ,则式(7)可近似为

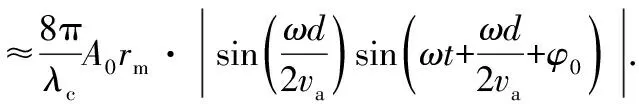
(8)

此时，近似条件为

(9)

rmω表示目标微动的最大瞬时速度，此约束条件较为宽松，在实际SAR系统中容易满足，因此式(8)具有普适性。式(8)表明，微动目标的DPCA信号幅度为正弦函数绝对值形式，且该正弦函数的频率同目标微动频率，幅度与目标微动幅度和频率有关。

同理，微动目标DPCA信号的相位可近似为

(10)

可见，其相位也表现出正弦调制特点。因此，微动目标DPCA信号可近似为正弦调幅-正弦调频信号。

2 Radon变换

如图2所示，假设f(t,ω)为平面(t,ω)上的二维函数，将原直角坐标旋转φ角得到新的直角坐标(u,v)，以不同的u值平行于v轴积分，所得结果即为Radon变换。其数学表达式为

δ(u-tcosφ-ωsinφ)dtdω.

(11)

可见，Radon变换实际上就是将(t,ω)平面上任意一条直线u-tcosφ+ωsinφ映射到(u,φ)平面上一点，本文用符号Pf(u,φ)表示f(t,ω)的Radon变换。

图2 Radon变换示意图Fig.2 Sketch map of Radon transform

3 多通道SAR振动目标检测

3.1 基于Radon变换的微动目标检测方法

由上面分析得到，振动目标回波在距离压缩域表现为沿方位向的直线，结合第3节分析Radon变换对直线的聚焦性能，本节对距离向压缩域信号进行Radon变换，则微动目标所在距离单元处将出现尖峰。设定门限Th，峰值超过该门限时，判定该距离单元存在微动目标，反之不存在。门限可设为局部数据标准差σ的倍数，即

Th=lσ.

(12)

对相应距离单元处的方位向信号作时频变换即可获得其微多普勒谱。具体操作流程如图3。

图3 基于Radon变换微动目标检测流程Fig.3 Flow chart of micro-motion targets detection based on Radon transform

3.2 基于时频分析和逆Radon变换微动目标检测方法

由第2节对Radon变换原理的分析，考虑平面(x,y)上一点(x0,y0),经过该点的直线u=x0cosθ+y0sinθ经三角变换后得

u=Bsin(θ+φ0),

(13)

对经过该点的直线连续改变角度θ进行Radon变换时，u随θ在平面(u,θ)上作正弦变化。所以，(u,θ)平面上一条正弦曲线对应着(x,y)平面上的一个定点(x0,y0)，可通过逆Radon变换求出该点。也即，逆Radon变换可实现正弦曲线到参数空间的映射。

由式(10)可得目标回波瞬时多普勒频率为

(14)

式中：第1项为载机运动产生的多普勒频率；第2项为散射点振动产生的微多普勒调制。

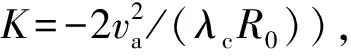
fm=Csin(θ+φm),

(15)

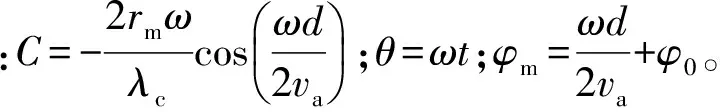
由第3节分析可知，微动目标产生的多普勒频率为正弦曲线。因此，微动目标散射点时频像可表示为

R(fm,θ)=δ(fm-Csin(θ+φm)).

(16)

由中心切片定理，逆Radon变换后图像为

ej2πkxx+j2πkyydfmdkxdky=

δ(x-Csinφm)δ(y-Ccosφm)，

(17)

式中：kx=vcosθ；ky=vsinθ。

可见，时频面正弦曲线fm=Csin(θ+φ)经过逆Radon变换后被映射到参数空间上的点(Csinφm,Ccosφm)。在逆Radon变换域提取图像特显点，则可根据特显点的坐标估计微动目标参数，如下式:

(18)

图4 基于逆Radon变换微动目标检测流程Fig.4 Flow chart of micro-motion targets detection based on inverse Radon transform

4 实验仿真分析

设置大小为400 m(方位向)300 m(距离向)的实验场景。场景内有2个静止目标和一个位于场景中心的振动目标。目标散射强度为1，振动参数为rm=0.02 m，ω=60π rad/s，φ0=45°。载机速度为150 m/s，波长0.06 m，带宽200 MHz，采样率PRF=1 536 Hz，脉宽Tp=1.2 μs，基线长度L=0.78 m，d=10vaT=0.98 m。经计算脉压前通道的信杂比SCR约为-13.01 dB。

4.1 DPCA距离压缩域

图5和图6为距离压缩后通道1和通道2回波信号的幅度图，可见在距离压缩域，振动目标与静止目标均表现为沿方位向直线。此时，能够检测到回波中存在3个目标信号，但是无法确认微动目标的存在。DPCA对消后，如图7所示，仅振动目标被保存。根据之前距离压缩域回波信号的分析，振动目标振幅远小于SAR距离分辨率，在距离压缩域表现为沿方位向的直线。而其他运动形式的回波信号在距离压缩域不会表现出直线形式，可根据此特性初步判断回波中存在振动目标。

图5 通道1原始回波Fig.5 Original echo of channel 1

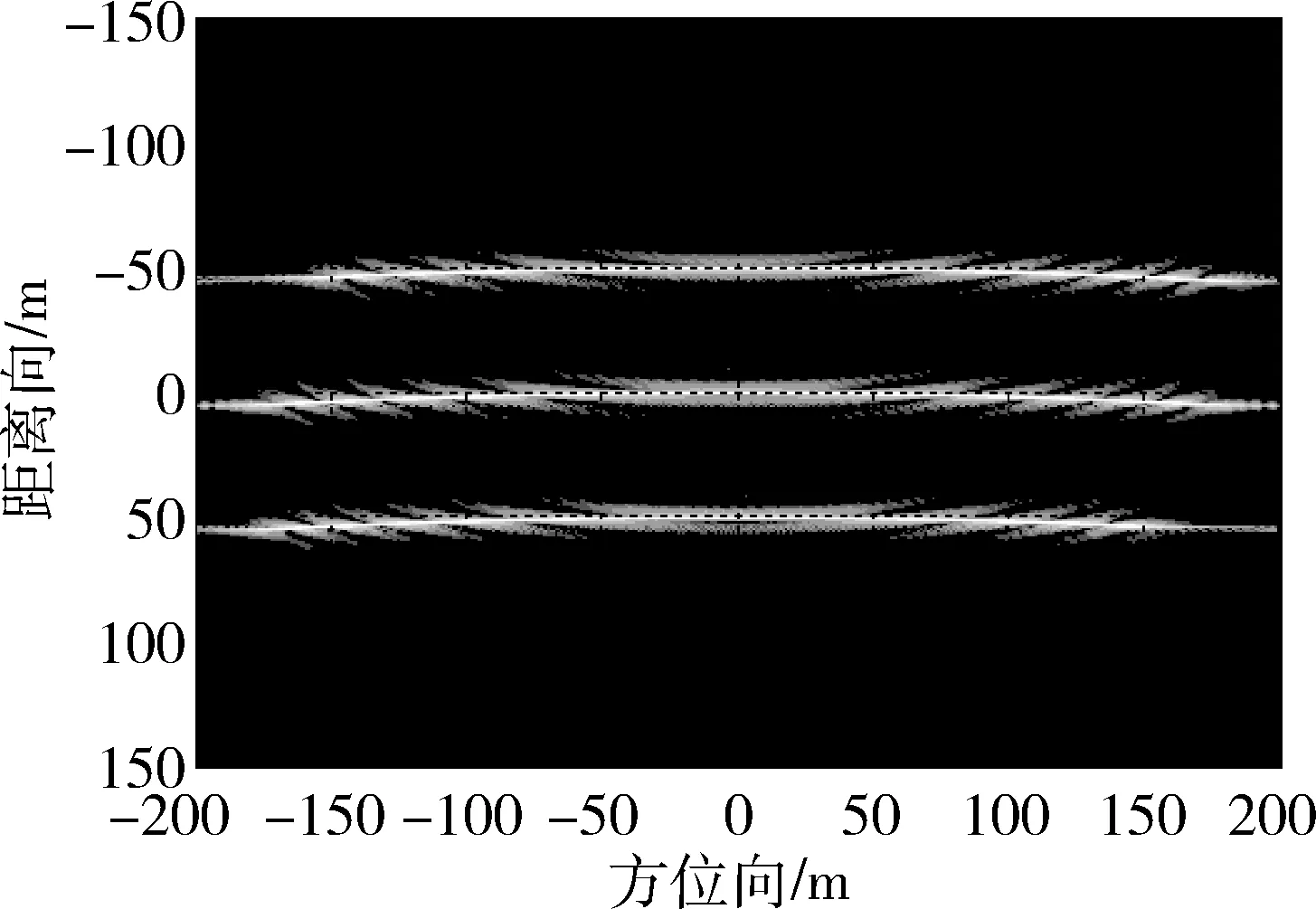
图6 通道2原始回波Fig.6 Original echo of channel 2

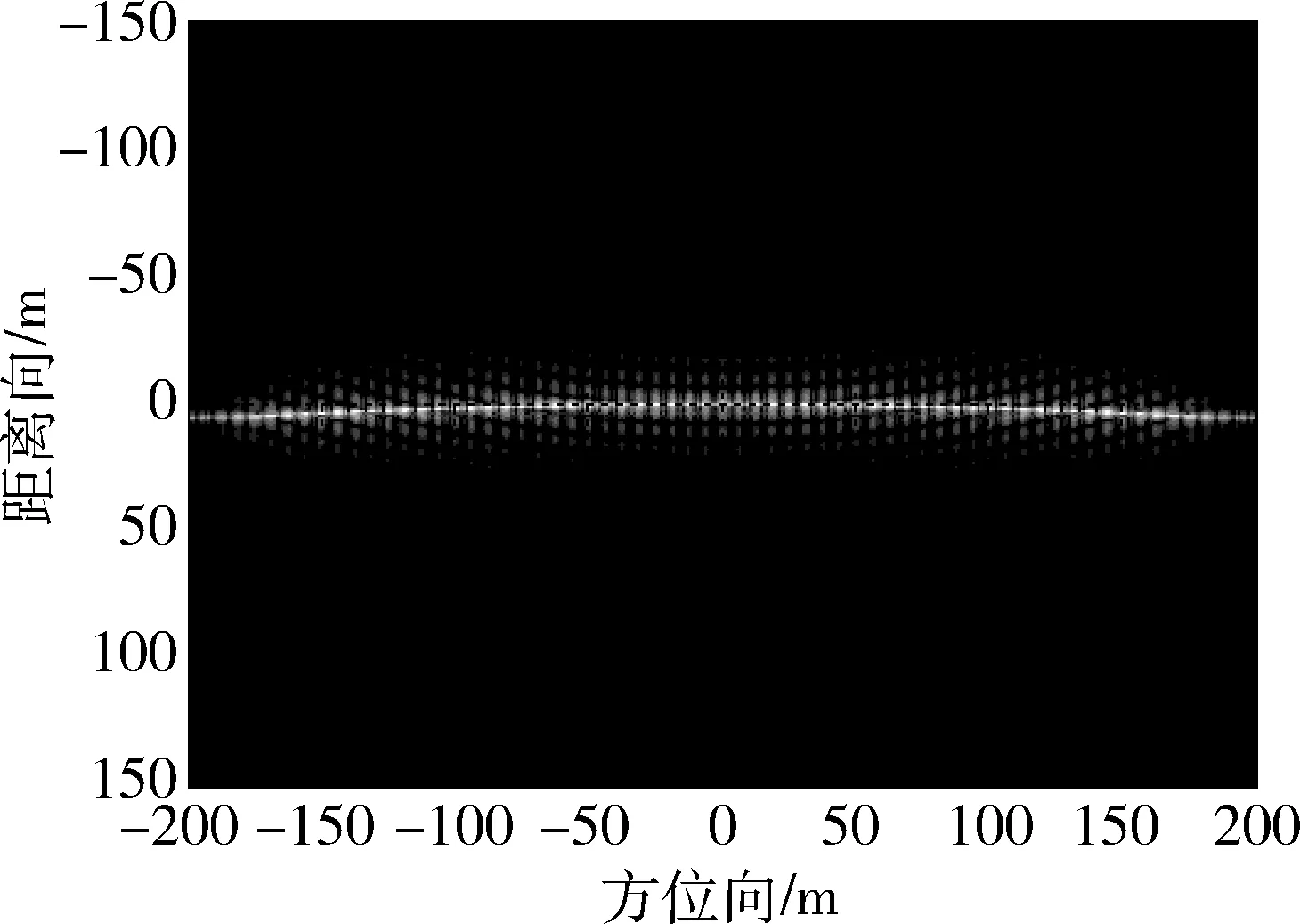
图7 DPCA对消后结果Fig.7 Result of DPCA

4.2 无噪和加噪时两种方法检测结果

按照2.1节的基于Radon变换微动目标检测方法，对DPCA信号进行Radon变换，在振动目标所处距离单元出现尖峰，如图8所示，与理论分析结论一致。

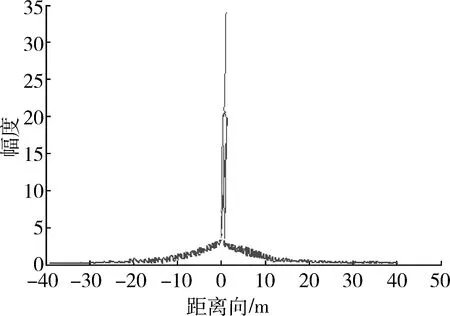
图8 DPCA信号Radon变换结果Fig.8 Radon transform on DPCA

而按照2.2提出的基于时频分析和逆Radon变换方法，对平动补偿后的信号进行时频变换得到微多普勒谱图如图9所示。可见微动引起的多普勒频移为正弦形式，与理论分析一致。利用逆Radon变换对正弦信号的聚焦性，对此谱图进行逆Radon变换后，在逆Radon变换域得到一个特显点，如图10所示，同样实现了振动目标的检测。

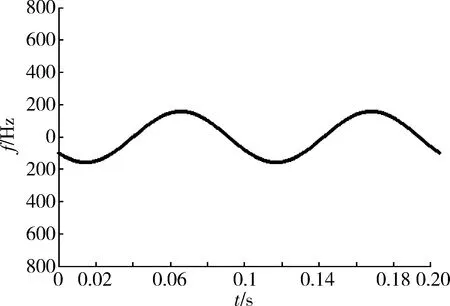
图9 微动目标回波谱图Fig.9 Spectrum of micro-motion target’s echo

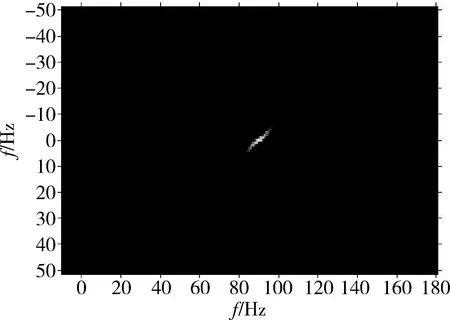
图10 微多普勒谱图的逆Radon变换Fig.10 Inverse Radon transform on spectrum

考虑噪声的影响，在通道信噪比为-5 dB时得到DPCA对消结果如图11。设置门限值为，由于噪声的影响，很难从对消结果中检测出振动目标。

图11 噪声条件下的DPCA信号Fig.11 DPCA with noise

采用基于Radon变换的检测方法，对DPCA信号进行Radon变换，得到强噪声条件下的变换结果如图12所示，在振动目标的距离单元上存在尖峰，实现强噪声条件下的检测。

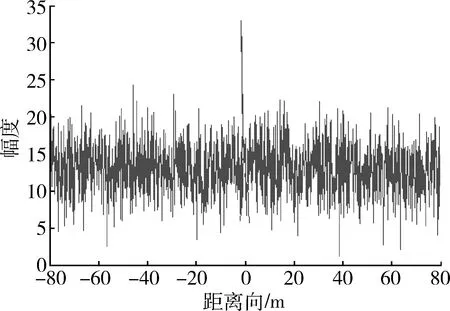
图12 强噪声条件下DPCA信号Radon变换Fig.12 Radon transform on DPCA with noise

采用逆Radon变换方法，对微多普勒谱图进行逆Radon变换，得到如图13所示结果。比较图13和图10，噪声对逆Radon变换影响很小，这是由于逆Radon变换对随机噪声不聚焦。因此，基于逆Radon变换的振动目标检测方法抗噪性好。

图13 强噪声下微多普勒谱图的逆Radon变换Fig.13 Inverse Radon transform on spectrum with noise

4.3 2种方法性能比较

为分析检测性能，在不同信噪比条件下进行1 000次蒙特卡罗仿真，得到如图14所示的检测性能曲线，其中红线代表基于逆Radon变换的检测性能，蓝线代表基于Radon变换的检测性能。可见，基于时频分析——逆Radon变换方法的检测概率在SNR≥7 dB时能达到80%以上；而基于Radon变换方法的检测概率在SNR≥-6 dB时能达到80%以上。因此，2种检测方法在强噪声条件下的检测性能良好，基于时频分析-逆Radon变换方法的检测性能优于基于Radon变换检测方法的性能，这是由于时频分析和逆Radon变换都具有抑制噪声的能力。

最后，根据检测结果，利用式(10)和(18)可估计振动参数。为分析参数估计性能，在不同信噪比条件下进行1 000次蒙特卡罗仿真，取参数估计结果与原始参数进行比较，得到参数估计误差曲线如图15所示。2种方法对振动频率和幅度的估计精度都在99%以上，且基于Radon变换的估计性能优于基于时频分析-逆Radon变换方法，这是由于基于时频分析-逆Radon变换方法在进行平动补偿和特显点提取时都存在不可避免的误差。

图14 2种方法的检测性能曲线Fig.14 Detection ability of two proposed methods

图15 2种方法的参数估计精度Fig.15 Parameter estimate precision of two methods

5 结束语

SAR微动目标检测是SAR图像解译和目标识别的关键。本文深入分析多通道SAR微动目标回波信号，指出：回波在距离压缩域表现为沿方位向的直线，可利用Radon变换对直线的良好聚焦性实现微动目标检测；目标微动引起的多普勒频率表现为正弦形式，可利用逆Radon变换对正弦曲线的聚焦性实现微动目标检测。

本文提出的检测方法利用DPCA技术实现杂波的稳健对消，利用Radon变换和逆Radon变换的良好聚焦性抑制了系统噪声对检测概率和参数估计精度的影响，拓宽SAR-GMTI的检测范围，为雷达目标识别提供了更加精细、更加稳定和更加可靠的目标信息，具有重要的理论价值和实际意义。

[1] CHEN Victor C, LI Fa-yin, HO Shen-shyang, et al. Micro-Doppler Effect in Radar: Phenomenon, Model, and Simulation Study[J].IEEE Trans. On Aerospace and Electronic Systems, 2006, 42(1): 2-21.

[2] CAI Cheng-jie, LIU Wei-xian, Fu Jeffrey, et al. Radar Micro-Doppler Signature Analysis with HHT[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(2):929-938.

[3] 张伟,童创明,张群,等.基于DPCA杂波抑制的地面振动目标微多普勒提取[J].系统工程与电子技术,2011,33(4):738-741. ZHANG Wei, TONG Chuang-ming, ZHANG Qun, et al. Micro-Doppler Extraction of Ground Vibrating Targets Based on SAR/DPCA Technique[J]. Systems Engineering and Electronics, 2011,33(4):738-741.

[4] 白雪茹,周峰,邢孟道,等.空中微动旋转目标的二维ISAR成像算法[J].电子学报,2009,37(9):1937-1943. BAI Xue-ru, ZHOU Feng, XING Meng-dao, et al. 2D ISAR Imaging Algorithm for Air Micro-Motion Targets[J]. Acta Electronica Sinica, 2009,37(9):1937-1943.

[5] 吴晓芳,刘阳,王雪松,等.旋转微动目标的SAR成像特性分析[J].宇航学报,2010,31(4):1181-1189. WU Xiao-fang, LIU Yang, WANG Xue-song, et al. Analysis of SAR Imaging Characterristics of Targets with Rotational Micro-Motion[J]. Journal of Astronautics, 2010,31(4):1181-1189.

[6] SPARR T, KRANE B. Time-Frequency Analysis of Vibrating Targets in Airborne SAR Systems[J]. IEE Proceedings-Radar Sonar and Navigation, 2003, 150(3):173-176.

[7] LIU Yong-xiang, LI Xiang, ZHUANG Zhao-wen. Estimation of Micro-Motion Parameters Based on Micro-Doppler[J]. IET Signal Process, 2010, 4(3):213-217.

[8] RÜEGG M, MEIER E, NUESCH D. Vibration and Rotation in Millimeter-Wave SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007,45(2): 293-304.

[9] 黄小红,贺夏,辛玉林,等.基于时频特征的低分辨雷达微动多目标分辨方法[J].电子与信息学报,2010,32(10):2342-2347. HUANG Xiao-hong, HE Xia, XIN Yu-lin, et al. Resolving Multiple Targets with Micro-motions Based on Time-frequency Feature with Low-Resolution Radar[J].Journal of Electronics and Information Technology, 2010,32(10):2342-2347.

[10] 张伟,童创明,张群,等.基于时频分析的双通道SAR自旋目标检测[J].航空学报,2011,32(10):1914-1923. ZHANG Wei,TONG Chuang-ming,ZHANG qun,et al.Rotating Targets Detection with Dual-Channel SAR Based on Time-Frequency Analysis[J]. Acta Aeronautica et Astronautica Sinica,2011,32(10): 1914-1923.

[11] 刘安娜,陈力,赵斐,等.基于DPCA-FrFT的三通道SAR-GMTI方法[J].电子学报,2011,39(9): 2091-2097. LIU An-na, CHEN Li, ZHAO Fei, et al.Study on DPCA-FrFT Based Multi-Channel SAR-GMTI[J]. Acta Electronica Sinica, 2011,39(9): 2091-2097.

[12] 于媛.基于Radon变换的LFM信号检测与参数估计[J].现代防御技术,2013,41(1):136-141. YU Yuan. Detection and Parameter Estimation of Linear Frequency Modulated Signals Based on Radon Transform[J].Modern Defence Technology, 2013,41(1):136-141.

[13] 张伟,童创明,张群.基于ATI技术和Radon变换的振动目标微多普勒提取[J].电子学报,2011,39(10):2431-2436. ZHANG Wei, TONG Chuang-ming, ZHANG Qun. Micro-Doppler Extraction of Vibrating Target Based on ATI Technique and Radon Transform in SAR[J]. Acta Electronica Sinica, 2011,39(10):2431-2436.

Micro-Motion Targets Detection with Dual-Channel SAR Based on DPCA and Radon Transform

CHEN Wen，ZHANG Zhi-jun，QIN Zhan-shi，XIANG Jian-jun，MA Ying

(AFEU,Aeronautics and Astronautics Engineering School, Shaanxi Xi’an 710038, China)

In order to detect micro-motion targets against strong ground clutter, the DPCA (displaced phase center antenna) is introduced to cancel the clutter in SAR(synthetic aperture radar)-GMTI(ground moving target indication) system, then two detection algorithm of micro-motion targets are proposed: the first one is based on the Radon transform, the other one based on time-frequency analysis and inverse Radon transform. Under the range-compressed data domain, the echo presents a beeline along the direction of azimuth. Similarly, the micro-motion can be detected by inverse Radon transform, because the micro-Doppler frequency produced by micro-motion is a sine wave which can be presented by time-frequency transform. Compared with the two algorithms, the method based on Radon transform can achieve better micro-motion parameter estimation result, while the method based on inverse Radon transform can realize bigger probability in detecting micro-motion target. Simulation results show effectiveness of the proposed algorithm.

synthetic aperture radar(SAR)；micro-motion target；displaced phase center antenna(DPCA); Radon transform; inverse Radon transform

2014-04-02；

2014-06-21

航空科学基金(20145596025)

陈稳(1990-)，男，湖南浏阳人。硕士生，研究方向为微波信号处理及工程应用。

通信地址：222300 江苏省连云港市东海县航空西路999号 E-mail：971930995@qq.com.

10.3969/j.issn.1009-086x.2015.03.027

TN958；TN957.51

A

1009-086X(2015)-03-0151-07