基于修正转弯模型的交互多模型跟踪算法*

苗伟，李昌玺，吴聪

(1.空军预警学院，湖北 武汉 430019； 2.国防信息学院，湖北 武汉 430010)

基于修正转弯模型的交互多模型跟踪算法*

苗伟1，李昌玺1，吴聪2

(1.空军预警学院，湖北 武汉 430019； 2.国防信息学院，湖北 武汉 430010)

临近空间高超声速飞行器具有极快的飞行速度和独特的机动模式，传统单模型跟踪方法不能对此类目标进行有效跟踪。提出了基于修正转弯模型的交互多模型跟踪算法，该算法修正了转弯模型，利用当前统计模型思想对目标角速度进行实时估计。首先分析了临近空间高超声速目标的特性，然后根据目标运动方程，对目标角速度进行实时估计，最后通过交互多模型实现对临近空间高超声速目标的跟踪。蒙特卡罗仿真结果表明，IMM跟踪算法能够有效跟踪临近空间高超声速目标，且跟踪的精确度、稳定性等明显优于单模型。

临近空间；高超声速目标；转弯模型；交互多模型

0 引言

临近空间高超声速飞行器是世界军事强国为争夺未来空天优势而竞相发展的重要武器，其极快的飞行速度和独特的机动模式，对现役防空系统构成了极大的挑战[1]。开展临近空间高超声速飞行器探测防御系统的关键技术研究，对维护我国国防安全具有重要的现实意义。

对空间的高速目标的雷达探测，国内外诸多学者从信号处理、信号波形以及雷达体制等方面进行了大量的工作[2]。文献[3]提出了基于参考加速度的跟踪模型，在目标弱机动时有较好的估计精度，但仍然存在目标运动模式简单等不足。文献[4]使用了参考加速度模型的交互多模型(interacting multiple model，IMM)算法，同时在对多基地雷达造成的非线性问题中采用了UKF(unscented kalman filter)滤波，取得了较好的跟踪效果。文献[5]采用交互多模型的结构，并加入未知角速度的匀速转弯模型，避免了目标机动，提高了滤波跟踪的距离精度和方位精度。

但单一的运动模型不能表征速度快、机动性强的高超声速飞行器的飞行轨迹。交互多模模型[6-7](IMM)是能够有效跟踪机动目标的模型之一，代价比较高。

鉴于此，本文提出了一种适用于临近空间高超声速飞行器的修正转弯模型(modified coordinate turn，MCT)，并将其引入IMM跟踪算法，拟实现对周期跳跃飞行的临近空间高超声速目标进行有效跟踪。

1 问题描述

临近空间高超声速目标具有区别于传统飞航导弹和弹道导弹的目标特性[1-2,8-9]：

(1) 飞行速度快：高超声速目标的飞行Ma数在5～25;

(2) 巡航高度高：高度范围在20～100 km；

(3) 机动能力强：加速度范围在0～5g，角速度范围在0～0.3 rad/s，巡航段为跳跃式飞行轨道，如图1所示；

(4) 目标后向散射截面积(radar cross section，RCS)小，一般在0.01～0.1 m2；

(5) 高超声速目标表面高温导致产生等离子体，会折射和吸收电磁波信号。

上述特点及临近空间高超声速目标独特的飞行轨迹如图1所示，给预警和拦截带来了很大的挑战。

图1 飞行轨迹示意图[1]Fig.1 Flight track sketch diagram

IMM跟踪算法步骤主要有交互输入、滤波计算、概率更新和交互输出，如图2所示。其核心是模型集的设计，子模型既要稳定可靠，简单易行，又要尽可能准确地描述目标实际机动情况。

图2 IMM工作原理图Fig.2 IMM working principle diagram

图2中，滤波器可以采用多种不同的跟踪模型，传统IMM跟踪算法对目标的非机动运动采用匀速(constant velocity，CV)模型，对机动运动采用匀加速(constant acceleration，CA)模型，对于机动更灵活的运动则采用“当前”统计(current statistical，CS)模型。IMM的计算过程主要包括输入交互、滤波计算、概率更新和输出交互4个步骤。具体计算过程参见文献[3,10]。

转弯模型(coordinate turn，CT)也称作协同转弯模型，能够较为真实地反映目标的机动范围和机动强度的变化，常用于常转弯速率运动目标的跟踪。将CT模型引入IMM中，多个模型并行工作，虽然能够增大对目标机动的覆盖范围，但是，针对临近空间高超声速目标，由于CT模型需要预先设定运动角速度,当目标周期跳跃飞行时，其转弯角速度变化较快，如果假定的角速度与目标实际运动转弯速率相近时，跟踪精度较高，否则跟踪精度下降，甚至导致跟踪失败。

2 基于修正转弯模型的交互多模型

MCT模型[11]在传统CT模型的基础上，假定目标角速度服从一阶时间相关过程，结合目标转弯运动的几何关系，并借助“当前”统计模型的思想，对目标转弯角速度进行实时修正，解决了传统CT模型不能有效描述临近空间高超声速飞行器运动特性的问题。当临近空间高超声速飞行器在高超声速飞行时，其相邻时刻的转弯角速度不可能发生突变，假设飞行器转弯角速度ω(t)服从一阶时间相关过程，其时间相关函数为指数衰减形式：

(1)

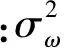
对时间相关函数Rω(t)应用Wiener-Kolmogorov白化程序后，ω(t)可用输入为白噪声的一阶时间相关模型来表示：

(2)

(3)

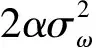
根据临近空间高超声速飞行器转弯运动的几何关系[12]有

(4)

由式(3),(4)可以得到MCT模型的连续时间系统状态方程为

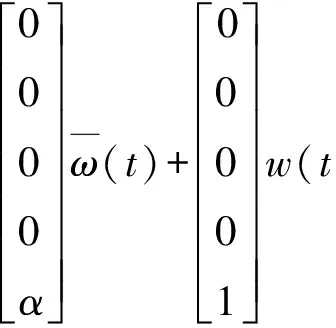
(5)

对飞行器转弯角速度的计算借助了“当前”统计模型的思想，假设ωmax表示飞行器转弯角速度正的最大值，ω-max表示飞行器转弯角速度负的最大值，则有

(6)

根据以上公式可推导出系统状态更新方程和协方差更新方程。在临近空间高超声速飞行器飞行过程中，假设飞行器在任何时刻的运动状态都可由给定的模型集{M1,M2,M3}来描述，初始模型概率记为

(7)

模型Mi转移到模型Mj是按照马尔可夫链转移的，转移概率Pij为已知：

(8)

然后进行CV模型、CA模型和MCT模型的IMM计算。

3 仿真分析

假设临近空间高超声速飞行器在临近空间进行跳跃机动飞行，飞行器起始状态为x(0)=(0 m,325 m/s,13 200 m,0 m/s,0 rad/s)，总飞行时间为1 000 s，机动频率α=1/60，最大转弯角速度ωmax=0.3 rad/s，飞行器发生机动时刻及对应加速度大小如表1所示。

表1 目标机动运动情况表Table 1 Target maneuver instance

假设主动雷达能够连续探测到飞行器在垂直平面的位置和速度(含有噪声)，雷达的量测周期T=1 s。模型间的转移概率

模型初始概率P=(0.25，0.50，0.25)。在Matlab7.1中进行100次蒙特卡罗仿真，当状态噪声和量测噪声均方根分别为r1=110，r2=110时，新模型与CS模型、Singer模型和Jerk模型在x和y方向上的位置均方根误差如图3所示。

仿真结果表明，传统CT模型出现了滤波发散，无法完成对临近空间高超声速飞行器的跟踪。从图3中可以看出，新模型的位置均方根误差要明显小于其他3个模型的，且新模型比较稳定，在飞行器机动变化较大时也能保持较好的跟踪状态。CS模型较Singer模型和Jerk模型的效果要好。这是因为，飞行器不是强机动的，加速度的变化率不是特别大，Jerk模型受机动频率的影响较大；Singer模型具有比CA和CV模型更宽的覆盖范围，具有较大的机动适应性；CS模型能较为真实地反映飞行器机动范围和强度的变化，是目前较好的实用模型。基于CV模型、CA模型和MCT模型的新模型既具有较宽的覆盖范围，又能及时修正“当前”飞行器机动角速度，使模型更符合临近空间高超声速飞行器的实际运动情况。

新模型与CS模型、Singer模型和Jerk模型在x和y方向上的速度均方根误差如图4所示。

从图4中可以看出，新模型的速度均方根误差要比其他模型的小，总体误差比较稳定，Jerk模型的速度误差大，CS模型的速度误差与新模型的相当，但是出现个别点的误差突变，例如在x方向t=60 s左右，出现较大的误差，这是因为此时飞行器发生了加速度从0跳变到45 m/s2的机动, 且角速度发生了较大变化。

使用Matlab中的tic和toc命令对各个模型的整个滤波过程进行计时，结果如表2所示。

表2 各模型跟踪耗时情况表Table 2 Time consuming of each model

从表2中可以看出，新模型跟踪算法的耗时长于其他单模型的，随着过程噪声和量测噪声的增大，各模型的耗时稍微有所增加。因为新模型跟踪算法在滤波的过程中，要完成输入交互、各模型的滤波计算和输出交互等步骤。且随着模型集中模型数量的增加，新模型的计算量也增加，但是从计时的结果可以看出，这个耗时量是可以接受的，最重要的是，新模型在外界环境发生变化时，其耗时量增加并不明显。这也说明了，每个模型都有一定的局限性，对于一个具体的战术情况而言，机动模型的性能不可能足够理想。

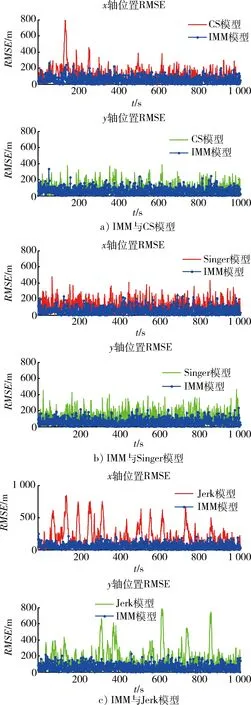
图3 位置均方根误差比较Fig.3 Cartogram of location root mean square error

图4 速度均方根误差比较Fig.4 Cartogram of velocity root mean square error

4 结束语

本文提出了基于修正转弯模型的交互多模型跟踪算法，该算法修正了传统转弯模型，利用“当前”统计模型思想对目标角速度进行实时估计。仿真结果表明，新算法能够实现对临近空间高超声速飞行器的有效跟踪，且稳定性强，跟踪精度明显高于单模型，不足之处在于计算量大于单模型。但是，新算法为临近空间高超声速飞行器的精确跟踪提供了一种思路，具有一定的现实意义和指导意义。如何根据临近空间高超声速飞行器不同阶段的运动特性来实时调整模型参数和模型数量，从而增加模型精度和减小运算量，是下一步的研究重点。

[1] 金欣,梁维泰，王俊，等.反临近空间目标作战若干问题思考[J].现代防御技术,2013,41(6):1-7. JIN Xin，LIANG Wei-tai，WANG Jun, et al. Discussion on Issues of Anti-Near-Space-Target Operation[J].Modern Defence Technology, 2013,41(6):1-7.

[2] 汪连栋，曾勇虎，高磊，等.临近空间高超声速目标雷达探测技术现状与趋势[J].信号处理，2014,30(1):72-85. WANG Lian-dong, ZENG Yong-hu, GAO Lei,et al. Technology Status and Development Trend for Radar Detection of Hypersonic Target in Near Space[J].Journal of Signal Processing, 2014,30(1):72-85.

[3] 关欣,赵静,张政超,等.一种可行的高超声速飞行器跟踪算法[J].电讯技术,2011,51(8):80-84. GUAN Xin, ZHAO Jing, ZHANG Zheng-chao, et al. A Feasible Tracking Algorithm for Hypersonic Aircraft[J].Telecommunication Engineering. 2011,51(8):80-84.

[4] 张燕鹏，薛俊诗，胡凯.基于多基地雷达的高超声速目标跟踪研究[J].火控雷达技术，2013,42(4):18-21. ZHANG Yan-peng，XUE Jun-shi，HU Kai. Study on Tracking Hypersonic Targets Based on Multistatic Radar[J].Fire Control Radar Technology, 2013,42(4):18-21.

[5] 吴超，单奇. 一种用于制导雷达的交互多模型跟踪滤波算法[J].雷达与对抗，2013,33(2):25-30. WU Chao，SHAN Qi. An Interacting Multiple Model Tracking and Filtering Algorithm for Guidance Radars [J].Radar & ECM, 2013,33(2):25-30.

[6] 孙庆鹏, 孔祥维, 卢聪聪，等.用于非线性机动目标跟踪的新型IMM 算法[J].智能控制技术电光与控制，2008,15(8):14-19. SUN Qing-peng, KONG Xiang-wei, LU Cong-cong，et al. Two New IMM Algorithms for Nonlinear Maneuvering Target Tracking [J].Electronics Oprics & Control, 2008,15(8):14-19.

[7] 周政, 刘进忙, 李振兴.基于STC-IMM结构的自适应多模型跟踪算法[J].控制与决策，2013,28(8):1226-1230. ZHOU Zheng,LIU Jin-mang,LI Zhen-xing. Adaptive Multiple-Model Tracking Algorithm Based on STC-IMM Structure[J]. Control and Decision, 2013,28(8):1226-1230.

[8] GRAHAM C, JOHNSON H, ALBA C, et al. Analysis of Modal Growth on The Leeward Centerplane of the X-51 Vehicle[R].USA: University of Minnesota,2009.

[9] Jeffrey S Robinson，John G Martin.An Overview of NASA′s Integrated Design and Engineering Analysis (IDEA) Environment[R].USA: American Institute of Aeronautics and Astronautics,2011.

[10] MAZOR E, AVERBUCH A, BAR S Y, et al. Interacting Multiple Model Methods in Target Tracking: a Survey[J].IEEE Trans. On Aerospace and Electronic Systems,1998,34(1): 103-123.

[11] 肖松，谭贤四，李志淮,等. 临近空间高超声速目标MCT 跟踪模型[J].弹箭与制导学报，2013，33(1)： 185-188. XIAO Song，TAN Xian-si，LI Zhi-huai，et al. Near Space Hypersonic Target MCT Tracking Model[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2013，33(1)： 185-188.

[12] 王华楠，刘高峰，顾雪峰.自适应转弯模型的交互多模型算法研究[J].弹箭与制导学报，2008，28(5)： 241-248. WANG Hua-nan, LIU Gao-feng, GU Xue-feng. Research on Adaptive Turning Model in Grid Multiple Model Algorithm[J]. Journal of Projectiles, Rockets, Missiles and Guidance,2008，28(5)：241-248.

Interactive Multiple Model Tracking Algorithm Based on the Modified Model of Turning

MIAO Wei1,LI Chang-xi1，WU Cong2

(1.Air Force Early Warning Academy, Hubei Wuhan 430019,China; 2.Institute of National Defense Information,Hubei Wuhan 430010,China)

The continuous success of hypersonic aircraft flight test in near space has become a real threat to space attack-defense counter，but the traditional tracking methods based on a single model cannot effectively track such target. A new interacting multiple model (IMM) tracking algorithm based on correction turn model is proposed, and the real-time state is estimated using the current statistical model. First, the near space hypersonic targets characteristics are analyzed. Then, the real-time target angular velocity is estimated by using the target motion equation. Finally, using the interacting multiple model, the near space hypersonic target can be successfully tracked. Monte Carlo simulations results verify the effectiveness of the proposed method, and the precision and the stability of tracking, which are better than that of the single model.

near space; hypersonic target; coordinate turn model; interacting multiple model(IMM)

2014-03-21；

2014-06-28

苗伟(1990-)，男，山西晋中人。硕士生，研究方向为高超声速目标。

通信地址：430019 湖北省武汉市黄浦大街288号空军预警学院研究生管理大队21队 E-mail：931245658@qq.com

10.3969/j.issn.1009-086x.2015.03.021

TN953;TP391.9

A

1009-086X(2015)-03-0113-06