箔条云干扰模型及仿真分析*

渠立永，刘君，秦建飞，吕振坚

(解放军理工大学 电磁环境效应与光电工程重点实验室，江苏 南京 210007)

箔条云干扰模型及仿真分析*

渠立永，刘君，秦建飞，吕振坚

(解放军理工大学 电磁环境效应与光电工程重点实验室，江苏 南京 210007)

针对反雷达伪装中箔条云干扰方法分析了零记忆非线性变化法(ZMNL)的幅度分布和功率谱分布模型，通过ZMNL法对于箔条云回波信号的产生机理讨论了一种新的建模方法。根据上述数学模型，对箔条云回波进行了仿真与模拟，提出了对于反雷达伪装中的应用可行性。

反雷达伪装；箔条云；分布模型;仿真

0 引言

箔条干扰技术现在仍然是现代战争中反雷达伪装的一个重要组成部分。近年来，特别是海湾战争以后，各军事强国均投入了大量的人力和财力对传统的箔条材料进行革新，相继推出了毫米波箔条、垂直极化箔条和光箔条等新型干扰箔条材料。目前，箔条干扰材料已从单一功能向多功能复合箔条干扰材料和宽频干扰箔条等方向研究和发展。为了检验箔条的干扰性能，简单有效的方法就是通过计算机对实施箔条干扰的回波信号建模进行仿真；因此，箔条回波信号模型的建立对于研究抗箔条干扰技术的效果具有重要的参考价值。

从20世纪50年代初期开始，对箔条云的散射机理及其应用就得到了广泛而深入的研究，至70年代已经取得了较为成熟的理论成果，并且在实践中得到大量成功应用。如Pyati V P[1]探讨了箔条云电磁散射的统计特性，在半波长箔条服从空间均匀随机取向并忽略互耦影响的前提下得到箔条云后向散射截面积的概率密度分布为指数分布；杨学斌等[2-3]基于布朗运动模型研究了箔条云团的扩散问题等等。李金梁[4]等在不考虑箔条云整体运动的前提下研究了箔条云的电磁散射特性，分析了箔条云的回波信号幅度分布及功率谱特性。目前研究重点是对箔条云在大气中的扩散过程建立准确的模型以及箔条云团在飘降过程中雷达散射截面和由于飘降引起的雷达回波多普勒频谱扩展等问题。

1 ZMNL法的雷达杂波仿真

由于现代雷达的分辨率越来越高，使得相邻散射单元的回波在时间和空间上均存在一定的相关性。一般来说，当一个杂波单元内包含有大量独立散射体时，雷达杂波包络服从瑞利分布，所以目前箔条云干扰幅度分布采用这种分布：

(1)

功率谱分布采用高斯型，其归一化功率谱密度函数为[5-6]

(2)

式中：fc为杂波中心频率；σc为杂波均方谱宽。

目前对于雷达杂波的方法，较有代表性的主要有3种[6]，最常见的方法是零记忆非线性变化法(zero-memory non-linearity transform,ZMNL)法,即通过产生具有特定概率密度函数和功率谱密度函数的随机序列来描述杂波信号，可以实现雷达杂波的几种常用分布的仿真，但其应用受到功率谱形状等因素的制约。由于它易于实现，且在相关高斯序列产生以后速度较快，在目前相关雷达杂波仿真中得到较多应用。

根据ZMNL的基本原理[6]，其基本思想是，首先产生相关高斯随机过程，然后经过某种非线性变换得到所要求的相关随机序列。ZMNL法需要找到高斯序列与所需序列相关系数之间的非线性关系g(·)，且非线性关系随不同的分布而不同，故不能对协方差矩阵和概率密度函数进行独立控制。如图1所示[7],具体地说，要产生相关对数正态分布、韦伯分布、K一分布杂波序列的过程[8],所以用这种方法需要找出序列{v}与{z}的相关函数之间的非线性关系来求得相关序列{w}，即通过w的相关系数ρij和输出z的相关系数Sij之间的关系来确定H(ω)。

但是由于实际在确定过程中存在高斯超几何函数，故不易求其反函数来得到ρij和Sij的关系，一般的方法是画出ρij和Sij关系曲线存入一个表中，然后由给定的Sij再经查表以求得相应的ρij值。这在实际使用中是比较麻烦的。

图1 零记忆非线性变换法(ZMNL)原理图Fig.1 Zero-memory non-linearity transform

本文就是通过箔条云回波信号的产生机理来讨论其建模方法。

2 箔条云回波建模及仿真

2.1 箔条干扰特性分析

箔条干扰的实质是：箔条在交变电磁场的作用下感应交变电流，根据电磁辐射理论，这个交变电流要辐射电磁波，即产生二次辐射，使雷达荧光屏上显示类似噪声的杂乱回波以掩盖目标回波，从而对雷达起无源干扰作用。箔条干扰是目前使用最多的一种无源干扰手段。其回波信号受很多因素影响，如大气密度、湿度、气流等，因此只能从统计意义描述它的特性，如反射面积、极化和多普勒频移等。在干扰建模中，利用箔条云回波的以下性质[9-10]：

箔条干扰是大量随机分布的箔条振子的响应总和。箔条总的有效反射面积等于箔条数乘以单根箔条的平均有效反射面积。设箔条为半波长的理想导线，则单根箔条的有效反射面积[11]

σ1=0.86λ2cos4θ.

(3)

考虑箔条在三维空间的任意分布，则箔条的平均有效反射面积为单根箔条的面积在空间立体角中的平均值，即

(4)

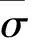
(5)

2.2 箔条回波信号的时域特性

箔条投放到空中后受大气密度、风速、气流等影响，严格意义上箔条干扰统计特性具有非平稳性，但考虑如下情况：

(1) 箔条在空中充分分散开，处于缓慢下降过程，并且进入接收天线波束的箔条数和退出波束的箔条数近似相等；

(2) 在箔条间隔2个波长以上时，可忽略偶极子间的互耦作用；

(3) 散射信号的振幅和相位互不相关，偶极子随机取向。

在上述条件下，可把箔条云散射信号看作平稳信号，且为各偶极子回波矢量和，合成回波信号为

(6)

式中:u为合成干扰信号幅度；θ为合成干扰信号相位；Ak为第k个箔条回波信号幅度；φk为第k个箔条回波信号相位。

当N很大时箔条云回波信号的幅度u为瑞利分布：

(7)

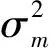
2.3 箔条云回波信号的多普勒效应

箔条从弹体内被抛散出去的一瞬间只有水平移动，速度很快，能产生较大频移，但时间很短。随后箔条随风速平移且下降，下降过程由于重量的不均衡和空气阻力作用以一定倾角绕重力线旋转，不同箔条的倾角和转速具体数值也不同。所以单根箔条的运动形式是平动和转动的组合。箔条云可以看作一种随机介质，其整体运动方式是在垂直下降运动上附加了一个风速。因此，箔条运动方式产生的多普勒效应有：

(1) 箔条平动引起多普勒频移，一般箔条随大气以风速沿一定斜角下落，其在雷达轴线方向的运动分量可以产生一个频移量：

(8)

式中:vα为箔条云运动的平均速度；α为vα方向与雷达轴线的夹角;λ为雷达信号波长。

(9)

(2) 箔条云中的箔条在下降过程中互相碰撞和分布的不均匀以及自身的转动运动使得箔条的平动速度不断起伏，这个速度的变化使其在观测方向的速度分量也不断变化，从而导致箔条和观测点之间的距离不断变化，因此回波频谱有一定展宽，其速度vc满足高斯分布。

(10)

根据上述2点可认为箔条云回波频谱是具有频移和一定展宽的高斯型函数。

2.4 箔条云回波信号的功率谱密度

假设箔条偶极子各向运动等可能，偶极子速度分布为麦克斯威尔函数q(v)的条件下，箔条回波电压的自相关函数可表示为

exp{-[2π/(aλ)]2τ2}，

(11)

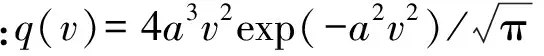
则箔条回波功率的协方差函数

(12)

对其作傅里叶变换得

(13)

式(13)表明，箔条回波功率的功率谱密度具有高斯函数形式。且当偶极子速度具有麦克斯威尔分布率时，若偶极子运动各向同性，则偶极子在雷达电波方向的径向速度分布具有高斯函数形式[12]，即与箔条云回波频谱为一展宽的高斯分布函数相符。

2.5 箔条云回波信号建模

根据箔条云回波信号为各偶极子回波信号矢量和的产生机理，设雷达一分辨单元内有k根箔条，入射雷达信号s(t)=exp(j2πf0t)，则对每一根箔条其回波信号有以下变化：

(1) 箔条平动引起多普勒频移：

(14)

(2) 箔条云内部互相碰撞及箔条转动的径向速度分量vr引起多普勒频移fd2。vr服从高斯分布：

(15)

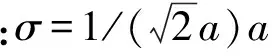
根据上述数学模型，对箔条云回波进行模拟：

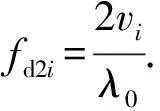
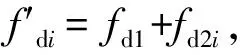
(3)第i根箔条的回波信号为

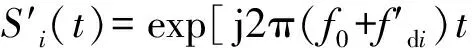
(4)总的箔条云回波信号为

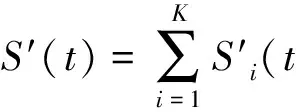
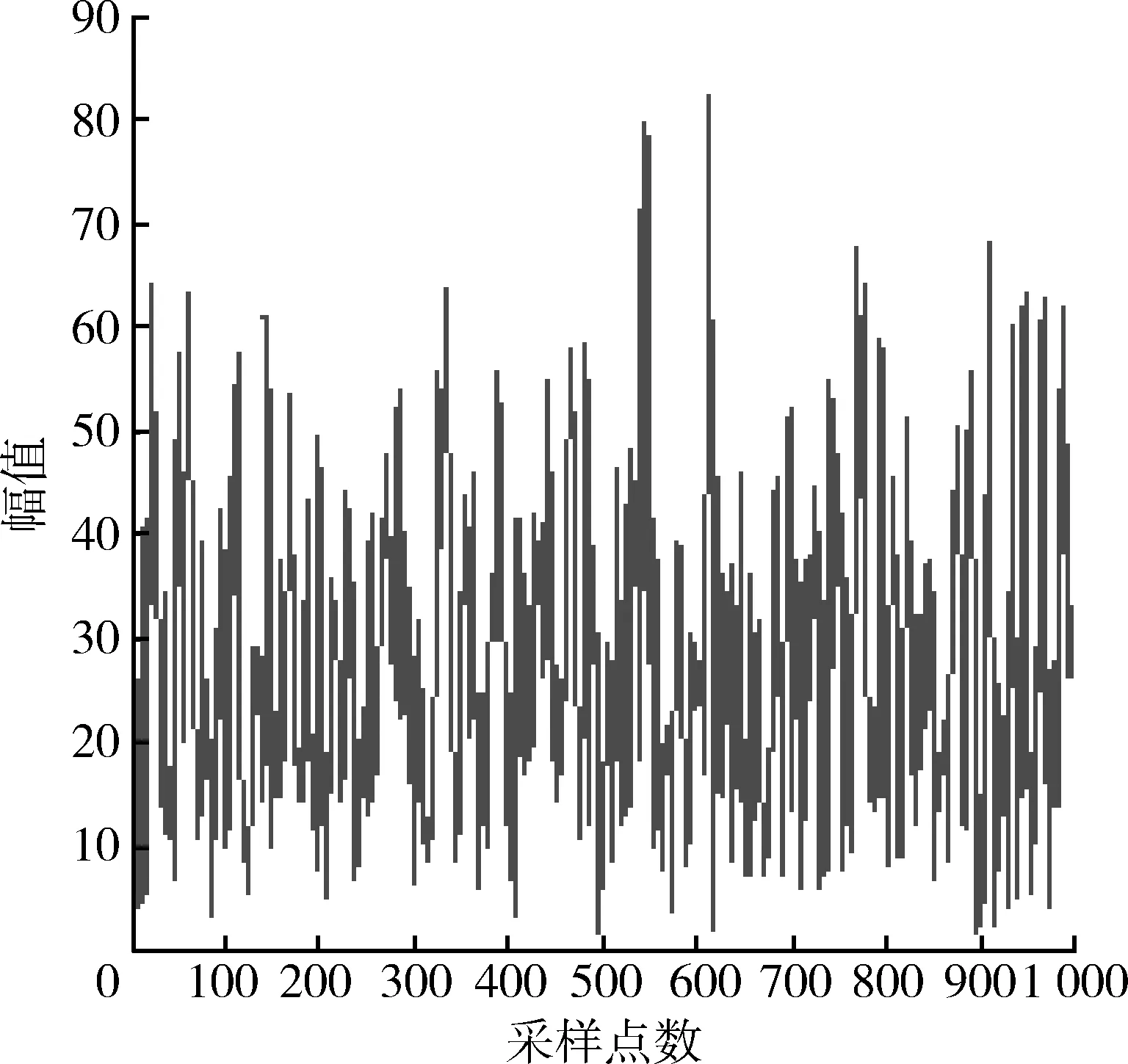
图2 箔条云干扰时域回波信号Fig.2 Time domain echo signal of chaff jamming

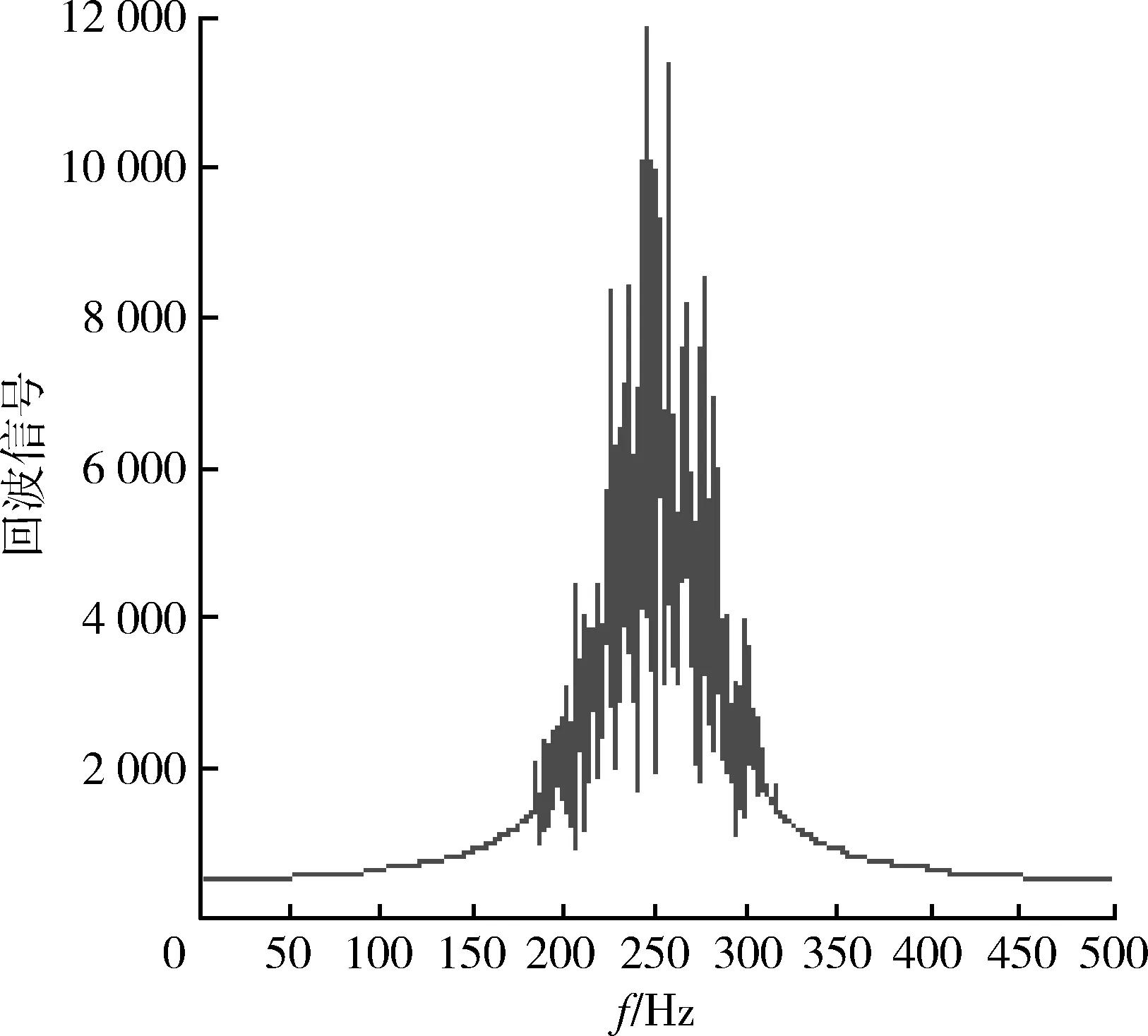
图3 箔条云干扰回波频谱Fig.3 Frequency echo signal of chaff jamming

设K=1 000，f0=200 Hz，fd1=50 Hz，σ=20，仿真结果如图2～5所示。可以看出仿真出的回波信号频谱符合高斯型，相位满足[-π,π]均匀分布，幅度概率密度函数满足瑞利分布，因此可把此随机信号序列近似看作箔条云回波信号。

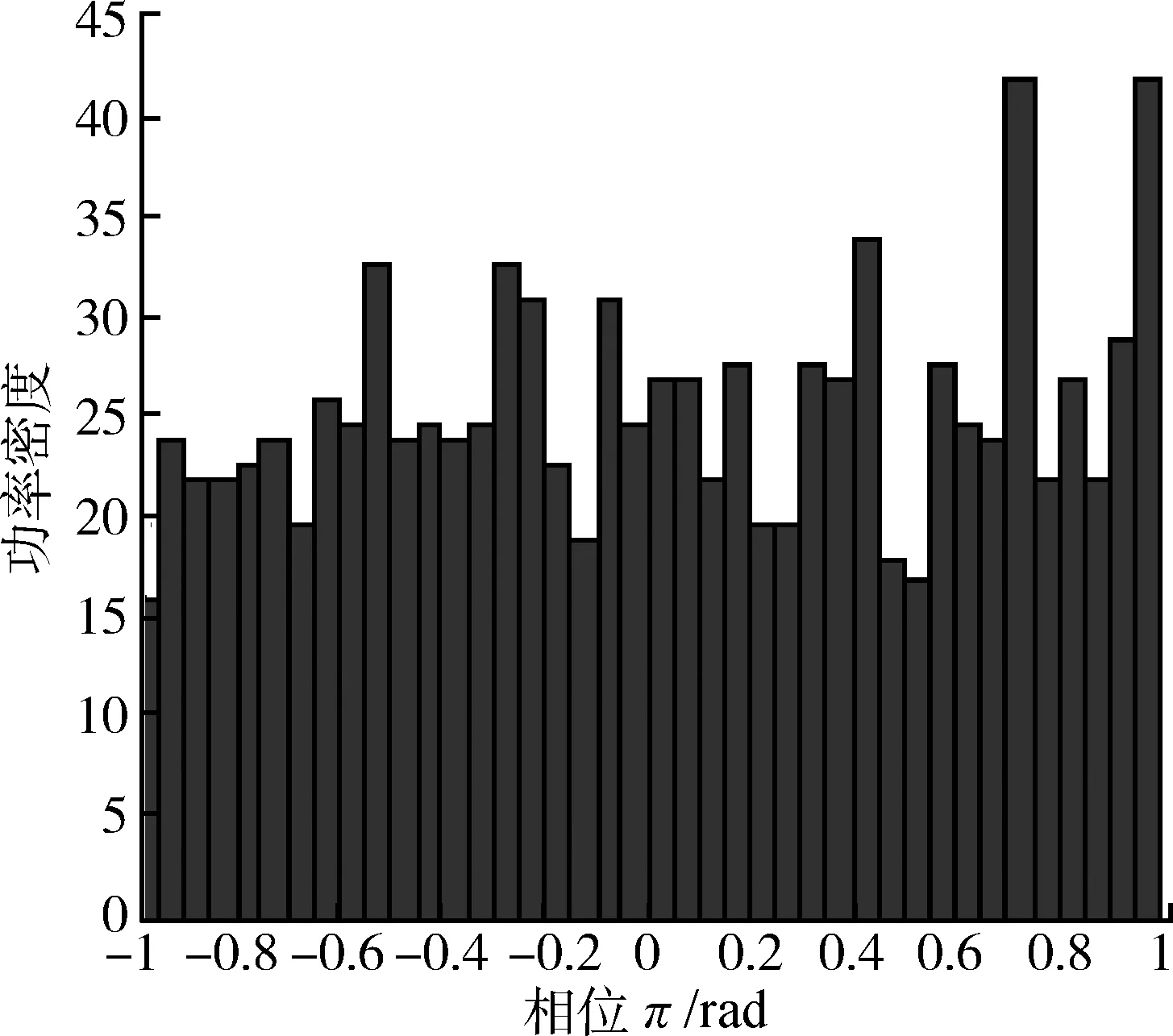
图4 箔条云干扰回波信号相位分布Fig.4 Phase echo signal of chaff jamming

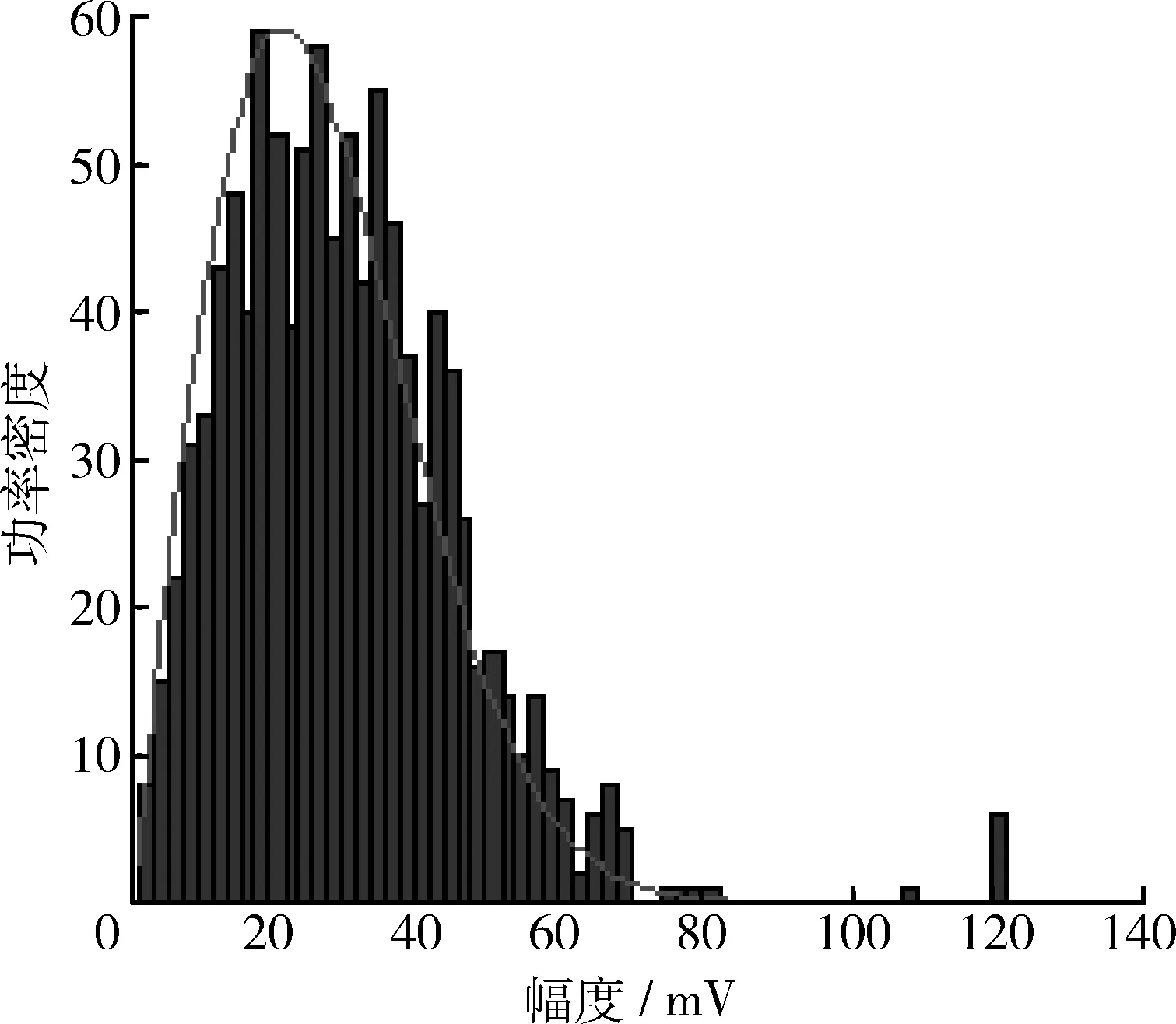
图5 箔条云干扰回波信号幅度Fig.5 Amplitude echo signal of chaff jamming

3 结束语

箔条干扰一直是一个不断研究的问题，本文根据现有的一些无源干扰信号模型，考虑到用ZMNL法仿真箔条云干扰信号中的计算问题，研究了基于其产生机理的建模方法。在反雷达伪装中，箔条干扰是一个快速而有效的技术，通过分析计算，给出了箔条云回波时域信号，回波频谱以及回波信号的相位分布和信号幅度，对反雷达伪装中箔条干扰具有重要的指导意义。而对于箔条干扰还需要进一步考虑回波信号的统计特性，以提高其干扰效果。

[1] PYATI V P．Statistics of Electromagnetic Scattering From Chaff Clouds[R]．ADA013929，1975.

[2] 杨学斌，吕善伟．箔条云团的后向散射截面积[J]．航空学报，1998，19(7)：81-83. YANG Xue-bin, LÜ Shan-wei. Backscattering Cross Section of Chaff Clouds[J].Acta Aeronautica et Astronautica Sinica, 1998,19(7):81-83.

[3] 杨学斌，吕善伟．箔条云团的布朗运动扩散模型[J]．北京航空航天大学学报，2000，26(6)：650-652． YANG Xue-bin, LÜ Shan-wei. Brown Motion Diffusion Model for Chaff Clouds[J].Journal of Beijing University of Aeronautics and Astronautics,2000,26(6):650-652.

[4] 李金梁，王雪松．箔条云的全极化频谱特性[J]．红外与毫米波学报，2009，28(3)：198-203． LI Jin-liang，WANG Xue-song. Full-Polarimetric Spectral Characteristics of Chaff Clouds [J].Journal of Infrared and Millimeter Wave 2009,28(3):198-203.

[5] MARIER L J. Correlated K-Distributed Clutter Generation for Radar Detection and Track[J]. IEEE on AES, 1995, 31(2): 568-580.

[6] 杨凤凤,周智敏. 基于 ZMNL 法的雷达杂波仿真[J]. 现代雷达,2003，25(9) ：22-24. YANG Feng-feng, ZHOU Zhi-min.Radar Clutter Simulation Based on ZMNL[J].Modern Radar,2003,25(9) : 22-24.

[7] 陈静. 雷达箔条干扰原理[M].北京：国防工业出版社，2007. CHEN Jing. Radar Chaff Jamming Principles[M].Beijing: National Defense Industry Press,2007.

[8] JAMES L．CorrelatedK-Distributed Clutter Generation for Radar and Track[J]．IEEE Trans On AES，1995，31(2)：568-580.

[9] 刘景萍,黄文良，赵惠昌. 箔条云的反射特性研究[J]．弹道学报,2000，12(3)：50-54. LIU Jing-ping，HUANG Wen-liang,ZHAO Hui-chang. Reflecting Signal of Chaff for Radio Fuzes [J]. Journal of Ballistics,2000,12(3): 50-54.

[10] 吴晓芳，李金良.SAR的箔条干扰技术研究[J].现代雷达，2010，32(7)：58-62. WU Xiao-fang, LI Jin-liang. A Study on Chaff Jamming Technology of SAR[J]. Modern Radar, 2010,32(7):58-62.

[11] 林象平.电子对抗原理[M].北京：国防工业出版社，1982. LIN Xiang-ping. Electronic Countermeasure Principles[M].Beijing: National Defense Industry Press,1982.

[12] 刘畅，占光．新的箔条散射截面数学模型及其仿真[J]. 吉林大学学报:信息科学版,2011,29(4):320-323. LIU Chang, ZHAN Guang. New Mathematical Model of Chaff’s RCS and Its Simulation[J]. Journal of Jilin University： Information Science ed,2011,29(4):320-323.

Model of Chaff Cloud and Simulation Analysis

QU Li-yong，LIU Jun，QIN Jian-fei，LÜ Zhen-jian

(PLA，University of Science And Technology，National Key Electromagnetic Environmental Effects and Electro-Optical Engineering，Jiangsu Nanjing 210007，China)

The zero-memory non-linearity transform (ZMNL) amplitude distribution and power distribution model are summarized in connection with anti-radar camouflage. A new modeling method of chaff cloud echo is presented based on its mechanism of generation. According to the model, the simulation and modeling on chaff cloud are calculated, and the feasibility is analyzed.

anti-radar camouflage; chaff cloud; distribution model; simulation

2014-04-19；

2014-06-16

渠立永(1974-)，男，江苏丰县人。讲师，硕士，研究方向为反雷达伪装。

10.3969/j.issn.1009-086x.2015.03.018

TN972+.4；TP391.9

A

1009-086X(2015)-03-0098-04

通信地址：210007 南京市海福巷1号解放军理工大学电磁环境效应与光电工程重点实验室伪装室

E-mail：quliyong@163.com