基于样条滤波的航天器相对运动检测方法*

孙福煜，王华

(国防科技大学 航天科学与工程学院，湖南 长沙 410073)

基于样条滤波的航天器相对运动检测方法*

孙福煜，王华

(国防科技大学 航天科学与工程学院，湖南 长沙 410073)

近距离相对运动检测在交会对接、航天器随动抓捕等领域有着重要的作用。基于三状态样条滤波算法，对接近航天器的运动状态进行实时预报并对其机动进行检测。首先构建两航天器的相对动力学模型并将其应用于三状态样条滤波算法中，通过检测滤波新息来对目标机动发生或消除进行判断，最后利用一个双脉冲交会的实例进行了仿真分析。仿真结果表明，该方法具有较高的精度和检测效率。

样条滤波；交会对接；机动检测；相对自主导航

0 引言

机动目标检测的应用领域非常广泛，在国防和民用方面都有重要的价值。它与现代导航技术相结合，可以实现对狭窄航道和港口内船只的预警和调度，也可以实现对空间运动目标的跟踪与拦截。它还常用于弹道导弹防御、精确制导和低空突防等[1]。

在追踪航天器的逼近过程中，目标航天器上安装的相对测量敏感器通常可获得两航天器间的视线距离、俯仰角、方位角和视线速率等测量参数中的全部或部分，且这些测量参数均带有一定的测量偏差[2]。而轨道规避控制需要的是两航天器的相对位置和相对速度，所以相对导航系统需要基于上述测量参数对两航天器间的相对位置和相对速度进行估计。文献[3-4]提出了一种模糊Kalman滤波新算法，利用航向角变化量和观测残差作为检测目标机动的参数；文献[5-7]针对滤波增益调整随意性问题，提出了一种修正的基于机动检测的机动目标跟踪算法；文献[8-10]提出一种改进的方差自适应机动目标跟踪算法，利用新息平方的统计量和当前加速度均值，对目标当前运动状态进行估计。

本文以上述文献为基础，基于三状态样条滤波，采用噪声协方差自适应方法对测量数据进行滤波，实现目标航天器对追踪航天器状态的估计与机动检测，最后进行了仿真验证。仿真结果表明，该方法具有较高的精度和检测效率。

1 相对动力学模型

1.1 坐标系定义

航天器轨道坐标系

航天器轨道坐标系Oxyz，其原点位于航天器质心，Oz轴由航天器质心指向地心，Oy轴与航天器轨道的角动量方向相反，Ox轴使得该坐标系成为右手直角坐标系，如图1所示。

图1 目标航天器轨道坐标系Fig.1 Target orbit coordinate system

特别的，当航天器轨道偏心率很小，可作近圆轨道假设时，该坐标系的Ox轴方向与航天器的速度方向是一致的。该坐标系常用于近程段相对运动的研究，此时Ox轴称为V-bar，Oy轴称为H-bar，Oz轴称为R-bar。

1.2 相对运动方程

在追踪航天器与目标航天器相对距离较近时，一般用追踪航天器、目标航天器相对动力学方程来描述2个航天器的相对状态。本文采用C-W方程[11]作为相对动力学方程，即

(1)

对于圆轨道或近圆轨道，当相对距离较小时，使用该方程计算的精度可以满足动力学计算的要求。

将式(1)可以写成状态方程的形式：

(2)

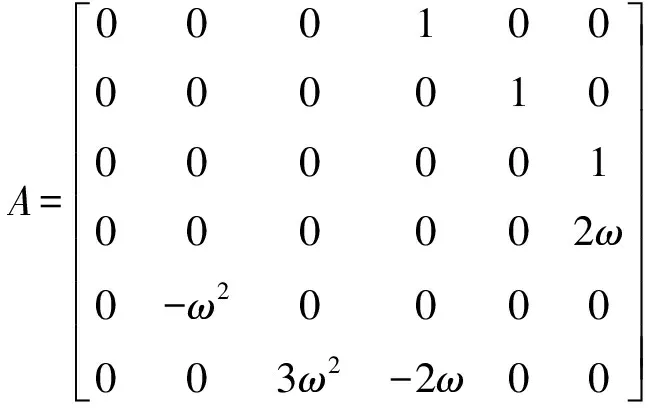
由状态方程式(2)可以得到状态转移矩阵：

(3)

式中：τ=ω(t-t0)。

若将状态转移矩阵分成4个3×3的方阵，即

(4)

令

(5)

并令初始条件X(t0)=X0，则可以求解任意时刻的状态变量：

(6)

对于n次脉冲机动，假设在ti时刻施加了脉冲Δvi，i=1,2,…,n，则式(6)可以表示为

(7)

2 基于样条滤波机动检测方法

三状态样条滤波是两状态样条滤波方法的扩展，即将二维状态变量(位置和速度)中增加加速度，对状态变量的位置、速度和加速度进行估计。

2.1 状态方程

在每个观测间隔T内，假设位置参数的三阶磨光函数(加速度的变化率)为常数S(k)，并计入一个随机加速度变化率εk，为正态白噪声序列。为了直接估计机动加速度，有状态方程

(8)

记状态方程为

Xk+1=ΦXk+ΒSk+Wk，

(9)

则

Wk=Βεk。

2.2 观测方程

假设状态方程和观测方程在目标航天器轨道坐标系下建立，则每个时刻目标的状态为轨道坐标系下的相对位置和速度矢量，观测方程即为相对测量设备的观测量(r，A，E)与目标状态(p，v，a)的关系。

相对测量设备探测数据(r，A，E)与航天器轨道系下的相对位置矢量(xr，yr，zr)T有如下转换关系：

(10)

2.3 三状态样条滤波算法

(1) 选取初值

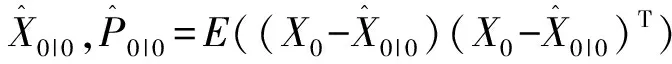
(2) 状态预测

(11)

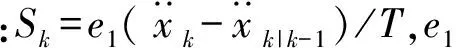
(12)

(3) 观测值预测

(13)

(4) 观测矩阵计算

(14)

(5) 计算增益矩阵

(15)

当检测到目标机动时，可以适当增大增益矩阵的模值。R为观测噪声协方差矩阵，为对角阵，对角线元素为噪声方差。

(6) 状态估计

(16)

(17)

2.4 机动检测方法

目标机动的发生使原来模型与实际的目标动态特性不一致，从而导致跟踪误差增大，新息过程发生急剧变化。通过检测滤波新息可对目标的机动作出判断，这是样条滤波机动检测决策的基本思想。

(18)

式中：n为观测维数，代表观测量的个数，对于位置x，y，z观测，n=3。

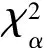
检测到机动以后，通过调节Qk和Rk，重新分配状态估计中预测部分和观测补偿部分的权重。

3 仿真结果

式(8)～(18)阐述了基于三状态样条滤波的航天器机动检测方法。本节通过一个近距离双脉冲接近的仿真算例来验证上述方法的合理性和准确性。

3.1 算例配置

表1 仿真试验参数设置Table 1 Simulation configuration parameters

3.2 仿真结果及分析

基于以上算例，采用三状态样条滤波算法对机动目标的状态进行滤波估计，得到如下图2，3所示结果。

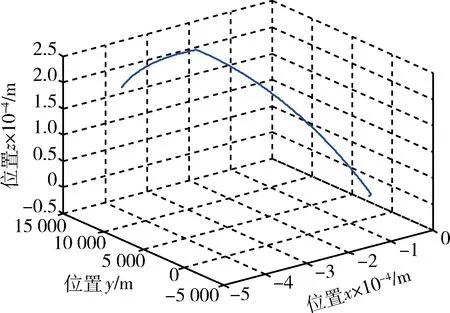
图2 相对位置变化曲线Fig.2 Change in relative position

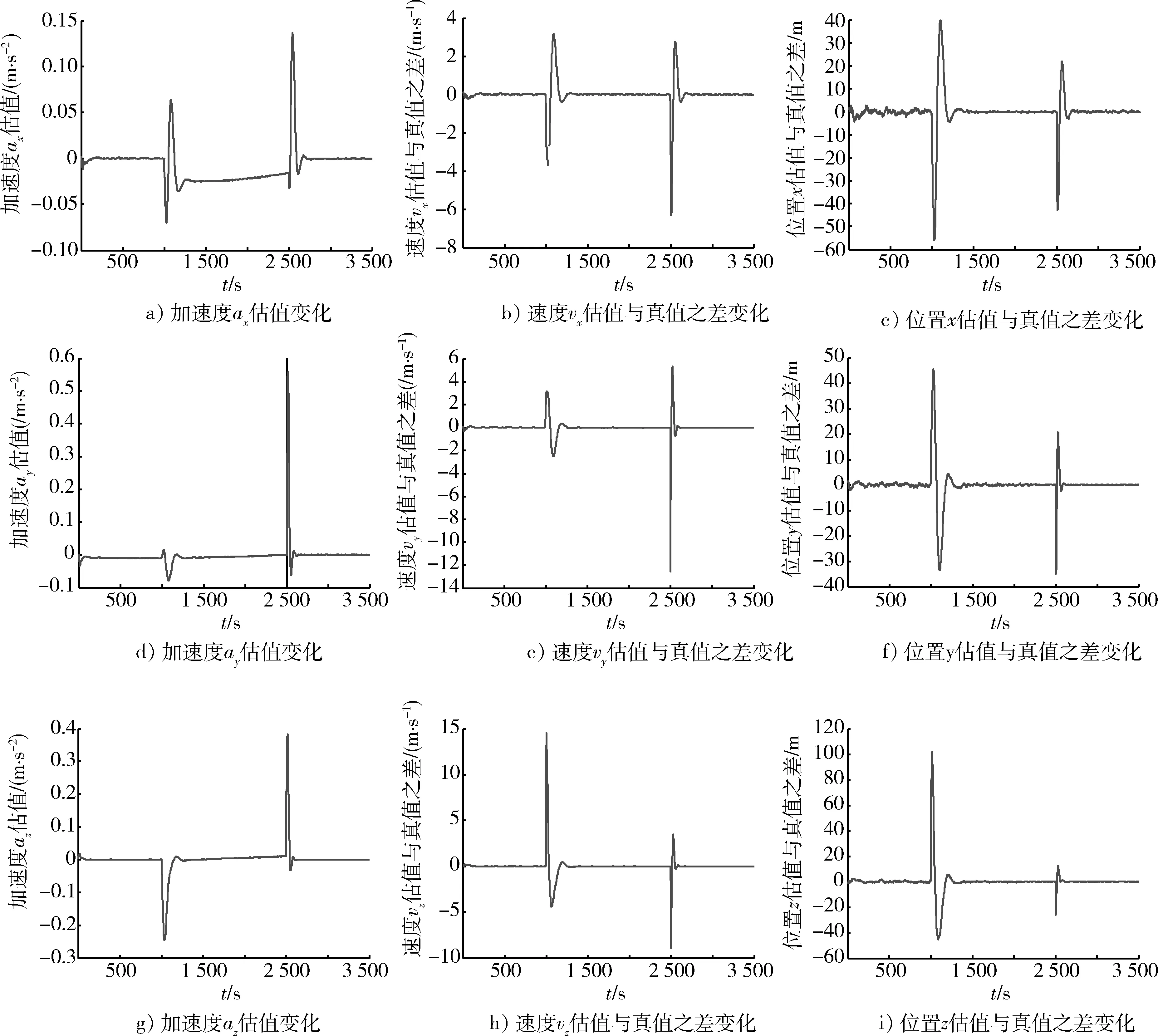
图3 滤波检测结果Fig.3 Result of filter

由图2可以看出，经过2次脉冲变轨后，追踪器与目标器的相对距离达到了预定的5 000 m左右。

由图3可以看出，当机动脉冲为正值，速度估值与真值之差曲线第1波峰为负，且幅度与脉冲值呈一定正比关系。即正值脉冲施加瞬间，速度估值与真值之差为负，脉冲值越大，速度估值与真值之差越小。原因是滤波所计算出的估计值中，一部分是依靠预测值，当脉冲为正，真实速度大于预估值，所以滤波所得到的估计值要小于真值。当脉冲为负值，现象和原因与上述相反。

位置估值与真值之差的正负和机动脉冲正负关系，与速度的现象一样。不同之处是位置估值与真值之差在首脉冲施加后，变化的幅值要大于第2次脉冲施加后变化的幅值。原因是在测量角度(仰角和方位角)误差一定的情况下，距离越大，位置误差就越大。并且测量距离误差也是随着位置的变化而变化，位置越远，测量距离误差就越大，这一点增强了上述现象的发生趋势。

将滤波估计值重新反算为测量数据，并与标准测量数据相减，得到滤波误差，与施加的量测噪声相比，可以用来比较滤波算法的性能。结果如图4～6所示。

由图4～6可以看出：

(1) 测量角度误差在第2次脉冲施加后，变化的幅值要远大于第1次脉冲施加后变化的幅值。原因是位置误差一定，距离越小，测量角度误差越大。这也与前面所述的位置误差与测量角度误差变化相一致。

(2)相对距离在2 397 s时刻达到最小值，约为4 824.421 m，此时距离误差中量测噪声和滤波误差均达到最小，分别为1 m和0.3 m。

图4 仰角滤波误差与量测噪声比较曲线Fig.4 Comparison of filter errors with measurement noise in pitching

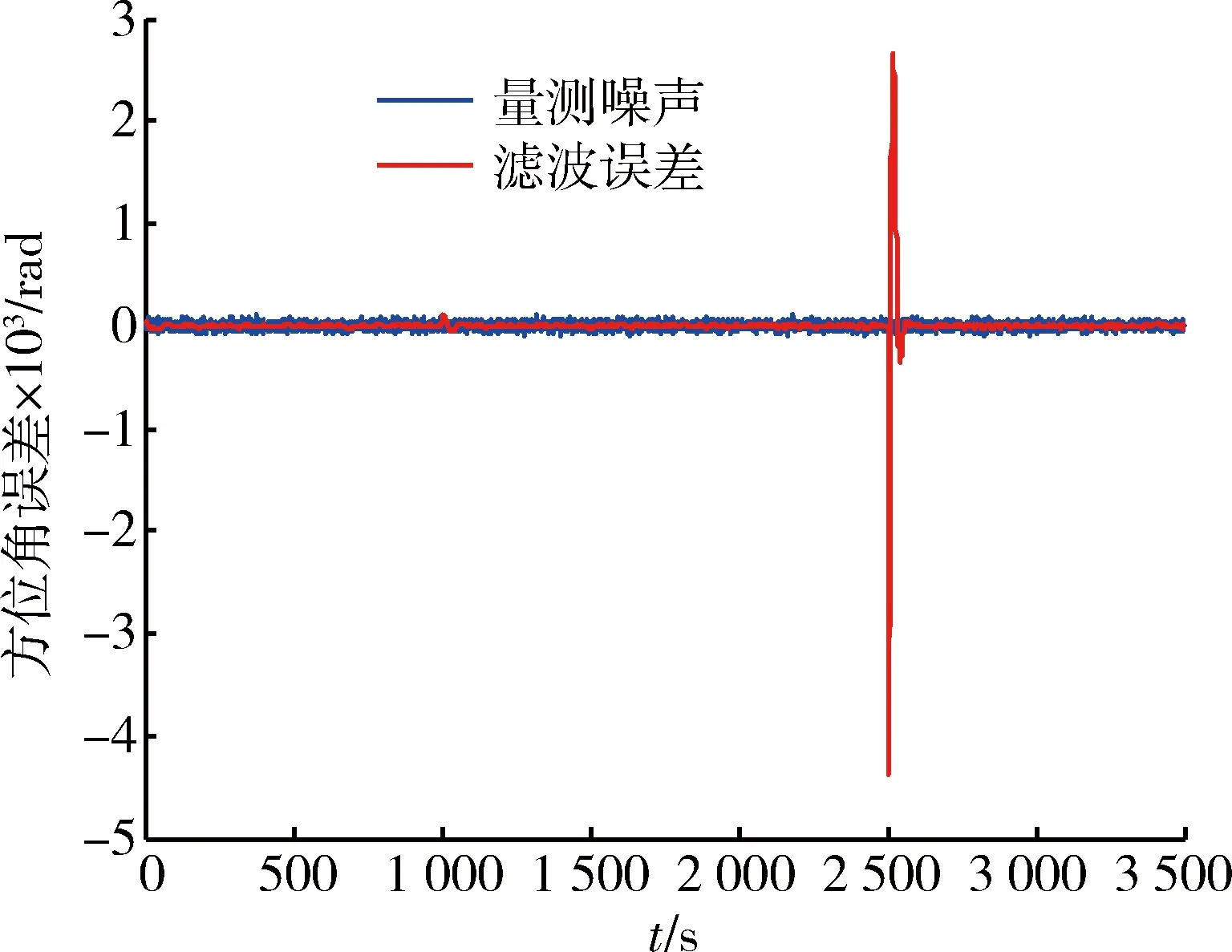
图5 方位角滤波误差与量测噪声比较曲线Fig.5 Comparison of filter errors with measurement noise in azimuth

图6 距离滤波误差与量测噪声比较曲线Fig.6 Comparison of filter error with measurement noise in range

(3)目标每次开始机动时，估计值存在一个巨大的误差(第1个波峰幅值很大)。对于样条滤波方法来说，误差第一波峰是不可避免的，因为样条滤波的当前时刻的加速度变化率是由上个时刻的数据预估的。也就是说，即便观测数据是完全精确的，机动检测也会有一个时刻的延迟。如果当前时刻实际变化与上个时刻相反，则预测与真实情况就完全相反，再加上由于观测误差引起的机动检测延迟，就出现了误差第1波峰。通过增加系统噪声进行补偿，可以有效减小第1波峰，但是在保证精度情况下调节能力有限。

(4)如果目标没有发生机动，仅从预测的角度来说，观测十几个点后就会收敛，收敛时间约为7 s。如果目标发生机动，就会出现误差第1波峰的现象，收敛时间就会相应的延长，需要观测几十个点的时间，约为200 s。

4 结束语

本文针对交会对接逼近段追踪器对目标器的接近过程，首先构建了两个航天器的相对动力学模型，然后采用三状态样条滤波算法对两航天器间的相对位置、速度和加速度进行实时估计，通过检测滤波新息来对追踪器机动的发生或消除进行判断，最后通过仿真验证了本文所提出方法的有效性。今后的工作可以围绕系统噪声自适应方面来开展。目标发生机动前，保持系统噪声为一个小量，保证估计精度；检测到目标发生机动后，适当增加系统噪声，可以有效减小第1波峰对系统带来的不利影响。

[1] 沈莹.机动目标跟踪算法与应用研究[D].西安：西北工业大学，2007. SHEN Ying. Tracking Algorithm and Application Research for Maneuvering Target[D]. Xi’an:Northwestern Polytechnical University, 2007.

[2] 刘也，余安喜，朱炬波，等.弹道目标实时跟踪中的滤波方法综述[J].宇航学报，2013，34(11)：1417-1426. LIU Ye, YU An-xi, ZHU Ju-bo. Survey of Filter Algorithms for Ballistic Target Real-Time Tracking[J]. Journal of Astronautics, 2013, 34(11): 1417-1426.

[3] 李鹏飞，黄建军，黄敬雄，等.一种模糊Kalman滤波机动目标跟踪的新算法[J].数据采集与处理，2009，24(4)：483-486. LI Peng-fei, HUANG Jian-jun, HUANG Jing-xiong, et al. Fuzzy Kalman Filter for maneuvering Target Tracking[J]. Journal of Data Acquisition&Processing, 2009,24(4):483-486.

[4] 王宏强，黎湘，刘丹，等.非线性系统中的机动目标跟踪算法[J].国防科技大学学报，2002，24(4)：57-60. WANG Hong-qiang, LI Xiang, LIU Dan, et al. Maneuvering Target Tracking in the Nonlinear System[J]. Journal of National University of Defense Technology, 2002, 24(4): 57-60.

[5] 关成斌，王国宏，王晓博.一种新的基于机动检测的机动目标跟踪算法[J].海军航空工程学院学报，2007，22(1)：148-150. GUAN Cheng-bin, WANG Guo-hong, WANG Xiao-bo. A New Algorithm on Tracking Maneuvering Target Based on Maneuver Detection[J]. Journal of Naval Aeronautical Engineering Institute, 2007, 22(1):148-150.

[6] 李理敏，龚文斌，刘会杰，等.基于自适应扩展卡尔曼滤波的载波跟踪算法[J].航空学报，2012，33(7)：1319-1328. LI Li-min, GONG Wen-bin, Liu Hui-jie, et al. A Carrier Tracking Algorithm Based on Adaptive Extended Kalman Filter[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1319-1328.

[7] 于洋，胡晓芳，刘砚菊.机动目标跟踪的改进自适应滤波算法研究[J].沈阳理工大学学报，2013，32(1)：56-59. YU yang, HU Xiao-fang, LIU Yan-ju.An Improved Adaptive Filtering Algorithm Research of Maneuvering Target Tracking[J]. Journal of Shenyang Ligong University, 2013, 32(1): 56-59.

[8] 孟庆虎，刘宝光.方差自适应机动目标跟踪算法研究[J].计算机仿真，2012，29(9)：10-13. MENG Qing-hu, LIU Bao-guang.Research on Improved Adaptive Tracking Algorithm for Maneuvering Targets[J]. Computer Simulation, 2012, 29(9):10-13.

[9] 唐政，郝明，周鹏，等.基于自适应卡尔曼滤波的机动目标跟踪算法[J].电子科技，2013，26(4)：78-81. TANG Zheng, HAO Ming, ZHOU Peng, et al.Tracking Algorithm for Maneuvering Target Based on Adaptive Kalman Filter[J].Electronic Science & Technology, 2013,26(4):78-81.

[10] 周航，冯新喜，王蓉，等.基于自适应扩展H∞滤波的机动目标被动跟踪[J].系统工程与电子技术，2013，35(2)：256-262. ZHOU Hang, FENG Xin-xi, WANG Rong, et al. Maneuvering Target Passive Tracking Based on Adaptive ExtendedH∞Filter[J]. Systems Engineering and Electronics, 2013, 35(2):256-262.

[11] 郗晓宁，王威.近地航天器轨道基础[M].长沙：国防科技大学出版社，2003:242-250. XI Xiao-ning, WANG Wei. Fundamentals of Near-Earth Spacecraft Orbit[M]. Changsha: National University of Defense Technology Press, 2003: 242-250.

[12] 汪雄良，周海银，朱炬波.三状态样条滤波与平滑[J].数学理论与应用，2002，22(1)：109-112. WANG Xiong-liang, ZHOU Hai-yin, ZHU Ju-bo. Three-States Pline Filter and Smooth Method[J]. Mathematical Theoryand Applications, 2002, 22(1): 109-112.

Relative Motion Detection Method of Spacecraft Based on Spline-Filter

SUN Fu-yu， WANG Hua

(National University of Defense Technology，College of Aerospace Science and Engineering，Hunan Changsha 410073，China)

The relative motion detection plays an important role in close rendezvous and docking, spacecraft follow-arresting and other fields. Based on three-state spline filter, the real-time forecasting of the chaser motion and detecting its maneuver is proposed. Firstly, a relative dynamic model of two spacecrafts is built and is applied to three-state spline filter algorithm, then the occurrence or elimination of chaser maneuver is judged by filter innovation. Finally, an example of double pulse rendezvous is presented and the filtering results are compared with the real measured values. The results show that this method has higher accuracy and detection efficiency.

spline filter；rendezvousand docking；maneuver detection；relative auto-navigation

2013-12-26；

2014-06-13

孙福煜(1989-)，男，辽宁沈阳人。硕士生，主要从事轨道动力学与控制、导弹攻防系统仿真等方面的研究。

通信地址：410073 长沙市开福区德雅路109号国防科大航天科学与工程学院 E-mail：sunfuyu89@126.com

10.3969/j.issn.1009-086x.2015.03.013

TN713；V448.2

A

1009-086X(2015)-03-0070-07