弹性支承梁固有频率影响因素研究*
2015-05-05马晨光刘昌洪陈晓岚
马晨光,刘昌洪,陈晓岚
(北京电子工程总体研究所,北京 100854)
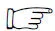
弹性支承梁固有频率影响因素研究*
马晨光,刘昌洪,陈晓岚
(北京电子工程总体研究所,北京 100854)
通过将折叠舵简化为梁模型来研究一种典型结构折叠舵频率的影响因素。对于梁内出现的弹性支承情形,采用了以分段表示的运动微分方程、简支和自由边界条件以及弹性支承处连续性条件来描述。根据梁的振动的基本方程,推导出弹性支承弯曲振动梁的频率方程的解析表达式,并利用数值方法计算出在不同条件下弯曲振动梁的频率,研究弹簧刚度,有效比刚度,以及支承点位置对固有频率的影响。
弹性支承;振动方程;弹簧刚度;比刚度;支承位置
0 引言
现代防空导弹为了提高作战单元的火力密度,减小发射筒(或箱)的外形尺寸,一般采用折叠舵面,折叠舵面与舵轴通常为铰链连接,并通过一定的展开机构来驱动。导弹的折叠空气舵由于折叠间隙的影响使空气舵的弯曲频率大幅度下降,进而容易引发颤振问题,导致飞行试验失败,目前该问题已成为折叠舵结构设计的瓶颈。本文通过将折叠舵简化为梁模型,研究不同因素对梁模型振动频率的影响。
国内外学者已经推导出在基本边界条件(两端简支、两端固定、悬臂梁)下等截面直梁的弯曲振动频率方程[1-2],并且对其进行了详细的分析,得出梁在弯曲振动时的固有频率会因为边界条件的不同而不同。
杨晓东等[3]研究了带有扭转弹簧支承梁的固有特性,宋殿义等[4]研究了两端线性弹簧支承梁的自振频率,并分析弹性支承刚度对频率的影响,马连生等[5]研究了不同梁理论之间简支梁特征值的解析关系。
本文以具有弹性支承的弹性梁的问题为例,具体分析了弹性支承的弹性系数、支承位置和材料有效比刚度对梁的振动频率和稳定性的影响。
1 折叠舵模型的简化
现代防空导弹一般采用折叠舵面,舵面与舵轴通常为铰链连接,连接部分的刚度为舵面固有频率的重要影响因素。一种典型的折叠舵结构如图1所示。

图1 舵面简化为梁模型Fig.1 Simplify the folding rudder into a beam
将舵面简化为梁过程如下:转轴处连接刚度是非线性的,为了便于研究,将2根转轴分别视为简支和弹性支承,支撑点位置xb对应折叠舵两转轴距离;弹簧弹性系数k对应折叠舵两转轴的连接刚度;主要研究上述因素对弯曲频率的影响。
2 梁的频率方程推导
如图2所示,具有弹性支承的等截面直梁,密度为ρ,截面弯曲刚度为EI,长度为l,左端M处为简支,右端N处为自由端,B处为弹性支承,弹簧弹性系数为k。
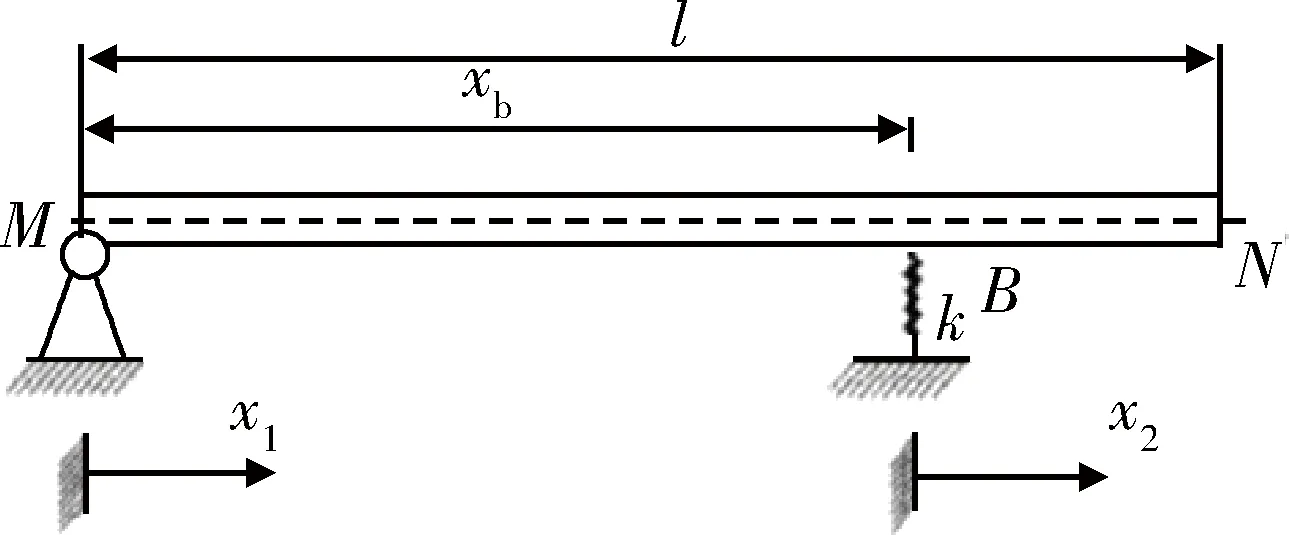
图2 带弹性支承的简支梁Fig.2 Simply supported elastic beams with internal elastic supports
目前,一些学者对含有弹性支承的梁的振动和稳定性问题的研究中,一般采用把弹性支承处的约束力用广义Dirac-delta函数表示为连续分布力[6-7],这样,运动微分方程中将出现多个δ函数,然后用积分方程法求解。例如XU M[8-9]等采用积分方程法研究了具有弹性支承弹性梁的自由振动和具有弹性支承的矩形板的自由振动问题;赵凤群等[10]分析了在切向均布随从力作用下含有弹性支承的非保守弹性矩形板的稳定性问题。
虽然积分方程法能有效地求解微分方程中含有多个δ函数的问题,但若方程中同时包含函数的偶数和奇数阶导数,或边界条件不是简支时,用积分方程法求解就有困难。本文建立了分段表示的运动微分方程[11],将支承的作用看成连续性条件,这样方程中将不出现δ函数。
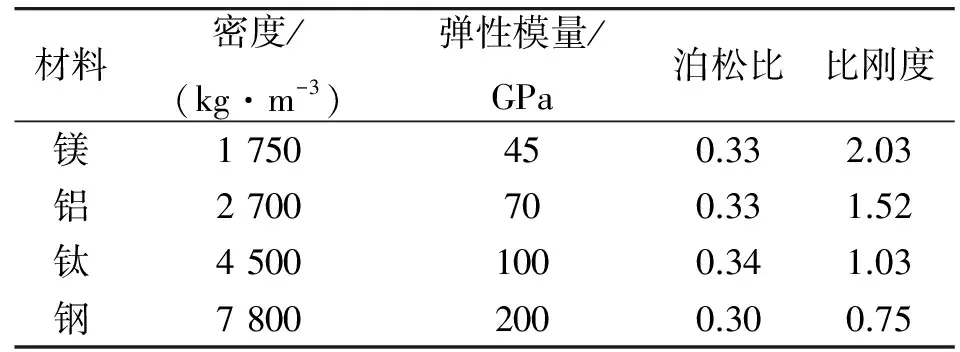
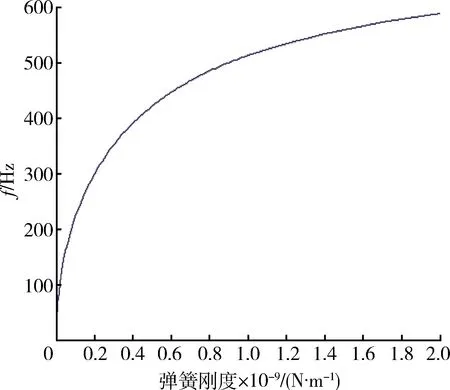
将梁分为2部分进行考虑,xi(i=1,2)表示梁横截面位置坐标,其中0 梁的弯曲振动微分方程为 (1) 设a2=EI/ρA,则式(1)变为 (2) 对式(2)的求解可以采用分离变量法。假定式(2)的解有如下形式 w(x,t)=φ(x)q(t). (3) 将式(3)代入式(2),化简后得 (4) 此方程两边必须等于同一常数,设此常数为,可得 (5) 设式(5)的基本解为φ(x)=esx,则特征方程为 s4-β4=0. (6) 其特征根为±iβ和±β,则其上述特征方程通解为 φ(x)=Asinβx+Bcosβx+Csinhβx+Dcoshβ, (7) 式中:积分常数A,B,C,D由边界条件确定,其典型边界条件见表1。 表1 梁横向振动典型的边界条件Table 1 Typical boundary conditions of bending vibration beams 由上述边界条件以及弹性支承处连续性方程可得 M处:ω1(0)=0,M1(0)=0; N处:M2(1-xb)=0,Q2(1-xb)=0; B处:ω1(xb)=ω2(0),θ1(xb)=θ2(0); M1(xb)=M2(0),Q1(xb)-Q2(0)=kω2(0). 将振型函数代入边界条件,可得 (8) 上述式(8)方程组有非零解的条件为 (-2(k/B)sin(βxb)sinh(βxb)cos(β(l-xb))· cosh(β(l-xb))-(k/B)sin(βxb)·sinh(βxb)·cosh(β(l-xb))cosh(β·(l-xb))-(k/B)sin(βxb)· sinh(βxb)cos(β(l-xb))cos(β(l-xb))-(k/B)· sin(βxb)sinh(βxb)sin(β(l-xb))sin(β(l-xb))+ (k/B)sin(βxb)sinh(βxb)sinh(β(l-xb))· sinh(β(l-xb))+(k/B)sin(βxb)sin(β(l-xb))· cosh(β(l-xb))cosh(βxb)-(k/B)sin(βxb)· cos(β(l-xb))sinh(β(l-xb))cosh(βxb)-(k/B)· sinh(βxb)sin(β(l-xb))cos(βxb)cosh(β(l-xb))+ (k/B)sinh(βxb)cos(β(l-xb))cos(βxb)· sinh(β(l-xb))+2sin(βxb)sinh(βxb)cosh(β· (l-xb))sin(β(l-xb))+2sin(βxb)sinh(βxb)· sinh(β(l-xb))cos(β(l-xb))+2sin(βxb)cosh(β· (l-xb))cosh(βxb)cos(β(l-xb))+2sin(βxb)· sinh(β(l-xb))cosh(βxb)sin(β(l-xb))+ 2sinh(βxb)sin(β(l-xb))cos(βxb)sinh(β· (l-xb))-2sinh(βxb)cos(β(l-xb))cos(βxb)· cosh(β(l-xb))-2cos(β(l-xb))cos(βxb)· sinh(β(l-xb))cosh(βxb)+2sin(β(l-xb))· cos(βxb)cosh(β(l-xb))cosh(βxb)=0, (9) 式中:B=EIβ3。 根据式(9)并利用数值方法[12]求出某些特定状态下的β,进而可以进一步求出梁的振动固有频率ω,并且可以分析不同参数对振动频率的影响。 首先验证上述理论的准确性,采用有限元分析软件进行建模计算,建立的模型如图3所示。 图3 梁的振动频率有限元计算模型Fig.3 Finite element model of bending vibration beams 其中梁的截面尺寸为0.03 m×0.03 m,长度为0.2 m,材料属性如下:密度为7 800 kg/m3,弹性模量200 GPa,泊松比为0.3。约束条件为一端简支,中间弹性支承,支承点位置距端点0.02 m。弹簧取值在106~107N/m范围内,理论值和计算值结果对比如图4所示。 由图4中曲线可以看出,理论值和软件仿真计算值基本一致,上述理论能够准确得出一端简支,中间弹性支承的梁的振动频率。 图4 有限元计算与理论推导结果对比Fig.4 Theoretical value and calculated value 3.1 材料有效比刚度对振动频率的影响 研究材料有效比刚度对频率的影响,仍然采取上文所建立模型,几何参数不变,在弹簧刚度变化范围为100~2 000 N/m时,改变模型材料属性,研究梁的频率的变化情况。材料参数特性如表2所示。 表2 几种典型材料参数Table 2 Typical material parameters 梁的振动频率和比刚度的关系如图5所示。 图5 不同材料梁的振动频率Fig.5 Frequency of beams for different materials 从图5中可以看出,梁的有效比刚度越大,振动频率越高。同时可以看到,当弹簧刚度较小时,不同材料的梁振动频率相差不大,说明弹簧刚度对振动的影响起主要作用,有效比刚度影响较小;当弹簧刚度值较大时,有效比刚度对振动频率影响较大,不同材料的梁振动频率差距明显。 3.2 弹簧弹性系数对振动频率的影响 固定支承位置,弹簧弹性系数从10~2×109N/m范围内变化时,梁的振动频率的变化规律如图6所示。 图6 梁振动频率随弹簧刚度变化图Fig.6 Frequency of beams for different spring stiffness 在弹簧支撑位置和材料参数保持不变的情况下,梁的固有频率随着弹簧刚度的增大而增加,但是弹簧刚度增大到一定值之后,固有频率的增长趋势趋于缓和。这说明当弹簧刚度在一定的低范围内(0~2×109N/m)变化时,对频率影响较大,当大于一定范围内时,对频率影响明显减弱。 3.3 弹性支承位置对振动频率的影响 固定弹簧的弹性系数等条件,改变弹簧的支承位置,研究不同支承位置下梁的振动频率的变化。 梁的振动频率和支承位置的关系如图7所示。从图中可以看出在特定的弹簧刚度范围内(k=100~2 000 N/m)梁的固有频率随着支承位置Xb值的增大而增大。支承位置离简支点较近时,频率随弹簧刚度变化不大,支承位置离简支点越远,弹簧刚度对频率的影响越明显。 图7 梁振动频率随支承位置变化图Fig.7 Frequency of beams for different support locations 本文推导了弹性支承等截面直梁弯曲振动的频率方程,从频率方程中得到在某些特定状态下的一阶固有频率,并分析了影响频率的参数及变化规律。支承条件确定的情况下,梁的固有频率会随着梁的有效比刚度的增长而增大,另外,固有频率随着支承位置xb值的增大呈现增大的趋势。梁的固有频率随着弹簧刚度的增大而增加,但是弹簧刚度增大到一定值之后,固有频率的增长趋势趋于缓和。这说明当弹簧刚度在一定的低范围内(0~2×109N/m)变化时,对频率影响较大,当大于一定范围内时,对频率影响明显减弱。 [1] 季文美,方同,陈松漠.机械振动[M].北京:科学出版社,1985. JI Wen-mei,FANG Tong,CHEN Song-mo. Mechanical Vibration[M]. Beijing:Science Press,1985. [2] THOMSON W T. Theory of Vibration with Applications[M].New Jersey:Prentice-Hall,Inc,Englewwood Cliffs,1972. [3] 杨晓东,金基铎,邹光胜.不同支承条件下弯曲振动梁的频率方程及特征值[J].沈阳航空工业学院学报,2000,17(4):1-6. YANG Xiao-dong,JIN Ji-duo,ZOU Guang-sheng. Freguency Equations and Eigenvalues of Different Supported Beams[J].Journal of Shenyang Institute of Aeronautical Engineering,2000,17(4):1-6. [4] 宋殿义,蒋志刚,陈北雁.弹性支承梁自振频率分析[J].江苏建筑,2005,19(1):30-31. SONG Dian-yi,JIANG Zhi-gang,CHEN Bei-yan. Analysis on Self-Vibration Frequency of Strut Beam[J]. Jiangsu Construction,2005,19(1):30-31. [5] 马连生,欧志英,黄达文.不同梁理论之间简支梁特征值的解析关系[J].工程力学,2006,23(10):91-95. MA Lian-sheng,OU Zhi-ying,HUANG Da-wen. Analytical Relationships of Simply-Supported Beam’s Eigenvalues Using Different BeamTheories[J]. Engineering Machanics,2006,23(10):91-95. [6] CHENG Y K,ZHOU Ding. Vibrations of Rectangular Plates with Elastic Intermediate Line-Supports and Cons Traits[J]. Thin-Walled Structures,2000,37(3):305-331. [7] HUANG M H,THAMBIRATNAM D P . Free Vibration Analysis of Rectangular Plates on Elastic Intermediate Supports[J]. Journal of Sound and Vibration,2001,240(3):567-580. [8] XU Ming-tian,CHENG De-lin. A New Approach to Solving a Type of Vibration Problem[J]. Journal of Sound and Vibration,1994,177(4):565-571. [9] 许明田,程德林.用积分方程法解板的振动问题[J].应用数学和力学,1996,17(7):655-660. XU Ming-tian,CHENG De-lin. Solving Vibration Problem of Thin Plates Using Integral Equation Method[J]. Applied Mathematics and Mechanics,1996,17(7):655-660. [10] 赵凤群,王忠民.点弹性支承的非保守矩形薄板的稳定性[J].西安理工大学学报,1998,14(4):398-403. ZHAO Feng-qun,WANG Zhong-min. The Stability of Non-Conservative Rectangular Plate with Spring Attachments[J]. Journal of Xi’an University of Technology,1998,14(4):398-403. [11] 赵凤群,王忠民,刘宏昭.转动惯量和弹性支承对非保守杆稳定性的影响[J].工程力学,2005,22(4):38-42. ZHAO Feng-qun,WANG Zhong-min,LIU Hong-zhao. Effects of Moment of Inertia and Internal Elastic Supports on the Stability of Non-Conservative Rods[J]. Engineering Machanics,2005,22(4):38-42. [12] 龚纯,王正林.MATLAB语言常用算法程序集[M].北京:电子工业出版社,2008. GONG Chun,WANG Zheng-lin. The Aggregate of MATLAB Algorithm Programming[M]. Beijing: Publishing House of Electronics Industry,2008. [13] 吴云书.材料的比强度和比刚度[J].宇航学报,1985,7(3):81-85. WU Yun-shu. The Specific Strength and Specific Stiffness of Materials[J]. Journal of Astronautics,1985,7(3):81-85. Influencing Factors of Elastic Supported Beams Frequency MA Chen-guang,LIU Chang-hong,CHEN Xiao-lan (Beijing Institute of Electronic System Engineering, Beijng 100854, China) The frequencies of a typical structure folding rudder are investigated by simplifying the folding rudder into a beam. For beams with internal elastic supports, the vibration equations at each section and continuous conditions at internal elastic supports as well as boundary conditions are given. Based on the bending vibration differential equation and its general solution of the beams, the analytical expressions of frequency equation of bending vibration beams with the elastic support are derived. And the frequencies are calculated by using numerical method. The influences on the frequency by the coefficient of the spring, the specific stiffness and the location of the elastic support are analyzed. elastic support; vibration equation; spring stiffness; specific stiffness; support location 2014-03-10; 2014-07-18 有 马晨光(1988-),男,河北衡水人。助工,硕士,研究方向为飞行器结构力学。 通信地址:100854 北京市142信箱30分箱 E-mail:billzhuyan@gmail.com 10.3969/j.issn.1009-086x.2015.03.008 TJ761.1+3;TJ760.3 A 1009-086X(2015)-03-0043-06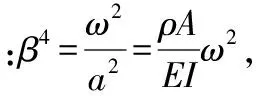

3 计算结果与分析

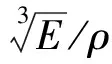


4 结束语
