自寻的导弹制导回路等效时间常数估算方法*

袁耀，高庆丰

(北京电子工程总体研究所，北京 100854)

自寻的导弹制导回路等效时间常数估算方法*

袁耀，高庆丰

(北京电子工程总体研究所，北京 100854)

给出了自寻的导弹制导回路模型，提出了二阶系统等效时间常数的估算方法。利用该方法对制导回路动力学系统进行等效时间常数的求解，最终得到制导回路五阶系统的等效一阶系统模型。通过等效前后制导回路系统的无量纲脱靶量仿真，验证了该等效时间常数估算方法的正确性。

制导回路；等效时间常数；估算方法

0 引言

自寻的导弹的脱靶量与导弹的末制导飞行时间关系密切，一般要求导弹制导飞行时间大于制导系统总的时间常数的10倍[1-4]，即制导回路的控制刚度大于10。制导回路的动力学滞后模型为高阶系统，为了在设计初期判断末制导飞行时间是否满足要求，需要求出制导回路动力学滞后模型的等效时间常数，将制导回路的动力学滞后环节用一阶等效滞后环节代替[5-9]。

1 自寻的导弹制导回路结构

图1给出了自寻的导弹的制导回路结构[3]，系统中存在3个动力学环节，分别为导引头动力学滞后环节、制导滤波器动力学滞后环节和自动驾驶仪动力学滞后环节。

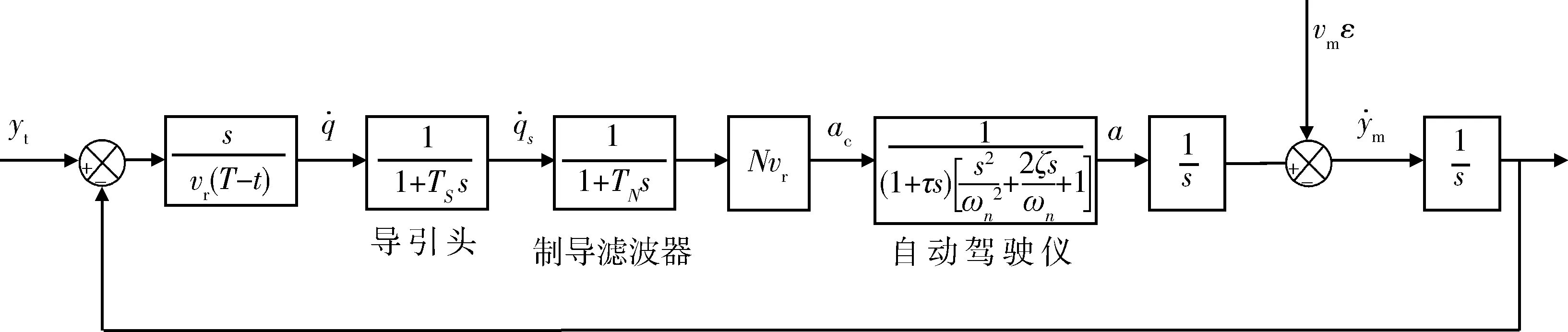
图1 自寻的导弹制导回路结构Fig.1 Guidance loop of homing missile

自动驾驶仪采用三回路自动驾驶仪，由三阶系统表示，其动力学模型为[10]

综上，制导回路可表示为

(1)

式中：a为导弹的法向加速度；N为导航比；vr为弹目相对速度。

2 二阶系统的等效时间常数

对于二阶系统，表征其振荡特性的是固有频率ωn和阻尼系数ζ。将系统的等效时间常数定义为动态响应达到其稳态值63%所需要的时间。在此定义下，该时间常数并不能准确地等于所谓“一阶时间常数”，但能较好地近似表征实际响应。二阶系统对阶跃输入的动态响应到达稳态值的63%时对应的ωnt值所求得的时间值t就是对应的时间常数τ[1]。

任何一个二阶线性系统的特性方程均可用如下形式表示：

(2)

二阶线性系统对单位阶跃输入的动态响应方程式为

(3)

ζ=1.0时，

h(t)=1-(1+ωnt)e-ωnt；

(4)

ζ>1.0时，

(5)

令h(t)=0.63，并将选定的ζ值代入相应方程，即可解出ωnt。按定义，该ωnt值就是对应于选定的ζ值的ωnτ数值。表1为利用这一方法解算得到的ωnt值。

表1 ζ与ωnt对应关系Table 1 Relationship between ζ and ωnt

沿用关于二阶系统近似等效时间常数的概念，可确定由2个一阶时间常数所组成二阶系统的近似等效时间常数[1]。

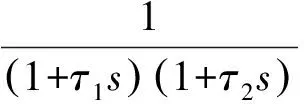
(6)

式(6)的特性方程为

τ1τ2s2+(τ1+τ2)s+1=0.

(7)

对比式(2)和(7)可知

(8)

(9)

由此可得

(10)

按下列步骤可近似确定与时间常数τ1+τ2等效的时间常数τ3：

(1) 利用式(10)计算得到ζ；

(2) 利用式(3)～(5)计算得到与ζ对应的ωnτ3；

(3) 利用式(8)计算得到ωn；

(4) 利用第(2)步和第(3)步的计算结果计算得到τ3。

3 制导回路等效时间常数估算方法

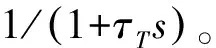
3.1 导引头加制导滤波器的等效时间常数

(1) 计算ζ

(2) 计算ωnτ4

查表1，ζ=1对应的ωnτ4=2.15。

(3) 计算ωn

(4) 计算τ4

即导引头加制导滤波器的等效时间常数τ4=0.322 5 s。

3.2 自动驾驶仪的等效时间常数

原自动驾驶仪模型中τ=0.3，ωn=35 rad/s，ζ=0.7，代入模型可得

则τ5=0.04。

与3.1节类似，可求得等效时间常数

τ6=0.349 2 s.

3.3 制导回路的等效时间常数

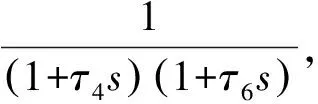
4 仿真验证[11-12]

4.1 不同导航比条件下仿真验证

取初始误差ε=0.2 rad，导弹速度vm=500 m/s，取导航比分别为N=3和N=4。对图1所示的制导回路和由第3节得到的等效回路模型进行仿真，2种导航比条件下由初始误差产生的脱靶量仿真结果见图2,3。由图2，3可看出，导航比N=3，在导弹制导飞行相对时间T/τT=8时，导航比N=4，在导弹制导飞行相对时间T/τT=10时，等效前后的制导回

图2 无量纲脱靶量曲线(ε=0.2 rad，N=3)Fig.2 Normalized miss distance (ε=0.2 rad, N=3)

路脱靶量均趋于0，等效模型可以较好地反映原高阶系统特性，该等效方法对不同导航比条件均适用。

图3 无量纲脱靶量曲线(ε=0.2 rad，N=4)Fig.3 Normalized miss distance (ε=0.2 rad, N=4)

4.2 不同初始误差条件下仿真验证

取导航比N=3，导弹速度vm=500 m/s，取初始误差分别为ε=0.3 rad和ε=0.5 rad。对图1所示的制导回路和由第3节得到的等效回路模型进行仿真，2种初始误差条件下由初始误差产生的脱靶量仿真结果见图4，5。由图4，5可看出，2种初始误差条件下，在导弹制导飞行相对时间T/τT=8时，等效前后的制导回路脱靶量都趋于0，等效模型可以较好地反映原高阶系统特性，该等效方法对不同初始误差条件均适用。

图4 无量纲脱靶量曲线(ε=0.3 rad，N=3)Fig.4 Normalized miss distance (ε=0.3 rad, N=3)

图5 无量纲脱靶量曲线(ε=0.5 rad，N=3)Fig.5 Normalized miss distance (ε=0.5 rad, N=3)

4.3 不同目标机动条件下仿真验证

分别取目标加速度at=10 m/s2和at=30 m/s2，对图1所示的制导回路和由第3节得到的等效回路模型进行仿真，2种目标机动条件下的脱靶量仿真结果见图6，7。由图6，7可看出，2种目标机动条件下，在导弹制导飞行相对时间T/τT=8时，等效前后的制导回路脱靶量都趋于0，等效模型可以较好地反映原高阶系统特性，该等效方法对不同目标机动条件均适用。

图6 无量纲脱靶量曲线(at=10 m/s2，N=3)Fig.6 Normalized miss distance (at=10 m/s2, N=3)

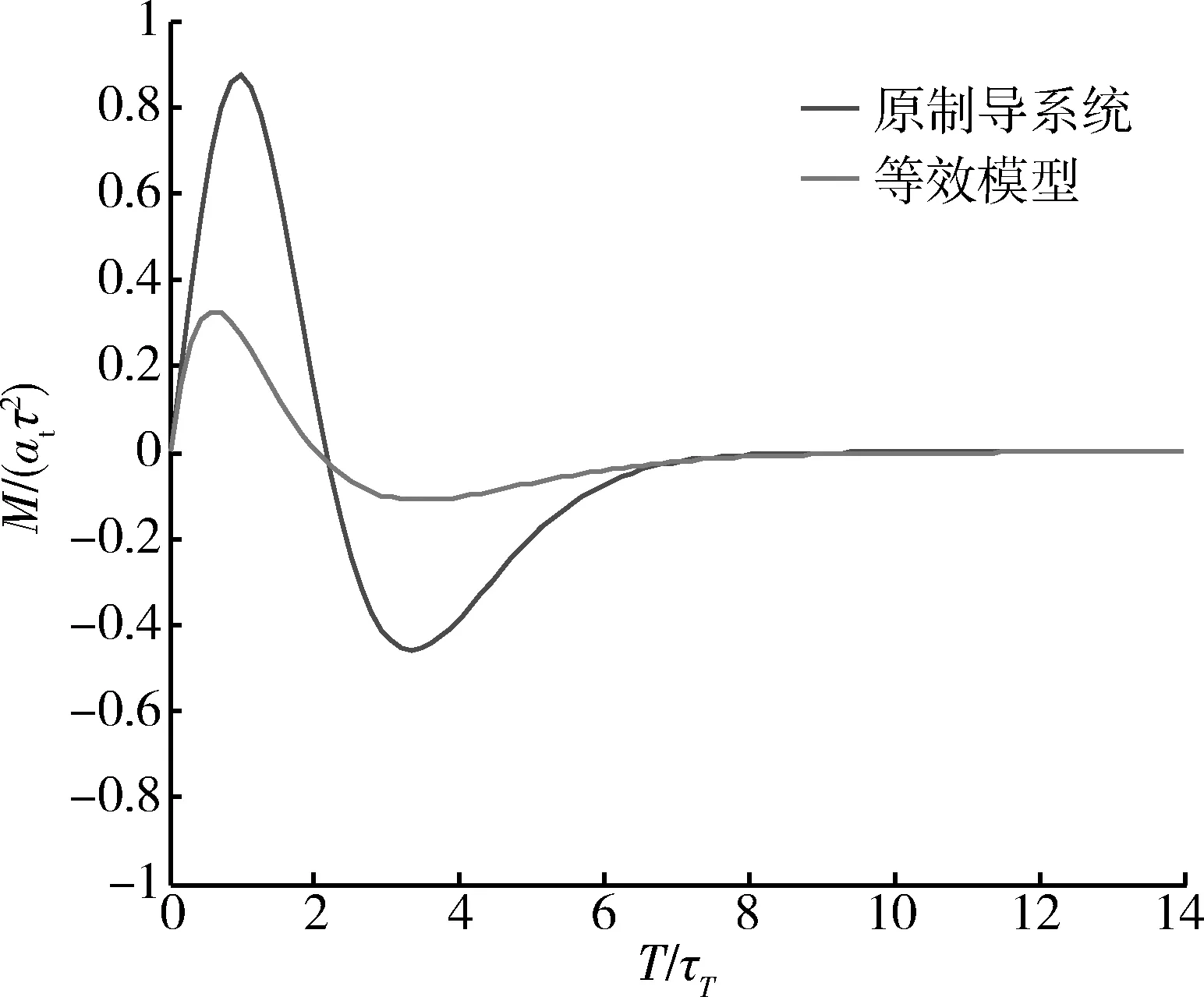
图7 无量纲脱靶量曲线(at=30 m/s2，N=3)Fig.7 Normalized miss distance (at=30 m/s2, N=3)

5 结束语

本文通过估算二阶系统的等效时间常数，求解出等效的一阶系统模型。经过等效求解，得到自寻的导弹制导回路高阶系统的等效时间常数，将制导回路的动力学滞后环节用一阶等效滞后环节来代替。制导回路仿真结果表明，该方法对不同导航比、不同初始误差、不同目标机动条件下均适用，简化后的一阶等效滞后环节可以较好地反映原高阶系统特性，可用于设计初期判断末制导飞行时间是否满足要求。

[1] 约瑟 J·哲尔格尔. 系统工程初步设计[M]. 北京：国防工业出版社，1965. Joseph J. Jerger. Systems Preliminary Design[M]. Beijing: Nation Defense Industry Press, 1965.

[2] 陈佳实. 导弹制导和控制系统的分析与设计[M]. 北京：中国宇航出版社，1984. CHEN Jia-shi. Analysis and Design of Missile Guidance and Control System[M]. Beijing：China Astronautic Publishing House，1984.

[3] ZARCHAN P. Tactical and Strategic Missile Guidance[M]. Washington D C: American Institute of Aeronautics and Astronautics, 1994.

[4] Rafael Yanushevsky. Modern Missile Guidance[M]. Boca Raton，London，New York：CRC Press，2007.

[5] 斯威特洛夫 B.T.，戈卢别夫 N.C.. 防空导弹设计[M]. 北京：中国宇航出版社，2004. Svetlov B T, Golubev N C. Air Defense Missile Design[M]. Beijing:China Astronautic Publishing House, 2004.

[6] 张望根. 寻的防空导弹总体设计[M]. 北京：中国宇航出版社，1991. ZHANG Wang-gen. Homing Air-Defense Missile Design[M]. Beijing：China Astronautic Publishing House，1991.

[7] 余超志，姚德源，夏咸松，等.导弹概论[M]. 北京：北京工业学院出版社，1986. YU Chao-zhi，YAD De-yuan,XIA Xian-song,et al. Introduction to Missile[M]. Beijing：Beijing Industry Institute Press，1986.

[8] 钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M].北京：北京理工大学出版社，2008. QIAN Xing-fang，LIN Rui-xiong，ZHAO Ya-nan. Dynamics of Missle[M]. Beijing：Beijing Institute of Technology Press, 2008.

[9] 赵善友. 防空导弹武器寻的制导控制系统设计[M]. 北京：中国宇航出版社，1992 ZHAO Shan-you. Guidance and Control System Design of Homing Air Defense Missile[M]. Beijing：China Astronautic Publishing House，1992.

[10] 胡寿松. 自动控制原理[M]. 北京：科学出版社，2001. HU Shou-song. Automatic Control Principle[M]. Beijing：Science Press，2001.

[11] 林德福，祁载康. 比例导引末导时间的等效时间常数估算法[J]. 系统仿真学报, 2006,18(11)：3026-3029. LIN De-fu, QI Zai-kang. Estimation on Engagement Time of Proportional Navigation Guidance System using Approximate Time Constant[J]. Journal of System Simulation，2006,18(11)：3026-3029.

[12] GARNELL P. Guided Weapon Control Systems[M]. 2nd ed. Qi Zai-kang, Xia Qun-li,Translated.Beijing: Beijing Institute of Technology，2004.

Estimation Method of Approximate Time Constant in Guidance System of Homing Missile

YUAN Yao，GAO Qing-feng

(Beijing Institute of Electronic System Engineering，Beijing 100854，China)

The guidance system model of homing missile is presented. The estimation method of approximate time constant in two-order system is proposed. Based on the method, the approximate time constant of guidance dynamic system is obtained with solutions, and the approximate one-order system model of the five-order guidance system is gained. By comparing the simulation results of the normalized miss distance between the two guidance systems, estimation method of approximate time constant is validated.

guidance loop; approximate time constant; estimation method

2014-03-13；

2014-07-20

有

袁耀(1984-)，女，湖南湘潭人。工程师，硕士，研究方向为导弹总体技术。

10.3969/j.issn.1009-086x.2015.03.010

TJ765

A

1009-086X(2015)-03-0055-05

通信地址：100854 北京市142信箱30分箱