多干扰源环境下多基地雷达主瓣干扰抑制方法*
2015-05-05王强张永顺司文涛
王强,张永顺,司文涛
(空军工程大学 防空反导学院,陕西 西安 710051)
多干扰源环境下多基地雷达主瓣干扰抑制方法*
王强,张永顺,司文涛
(空军工程大学 防空反导学院,陕西 西安 710051)
针对空间多干扰源方向未知时,干扰抑制效果差这一问题,提出了一种新方法。首先利用改进的MUSIC算法对干扰方位信息进行估计,重新建立干扰模型,然后再进行接收站之间联合干扰对消。结合仿真实验分析可知,经过以上2步处理,信号峰值幅度可达到0.05 V,输出信干噪比改善量约为25~30 dB。实验结果表明,该方法具有有效性。
多干扰源;多基地雷达;主瓣相消
0 引言
当天线主波束内存在多个干扰源的情况下,常见的自适应波束形成技术、极化滤波技术、自适应干扰相消技术均不能有效实现干扰抑制[1-2]。近年来,随着多基地雷达相关技术的逐渐成熟,其在雷达电子对抗、目标识别、成像等方面的应用越发广泛,特别是对“三大同步问题”的积极研究,确保了多基地雷达空间相干特性的有效发挥。空间相干多基地雷达,即多基地相参雷达,能够实现多个接收站间信号的联合处理,充分利用其丰富的站间信息资源。文献[3]中明确指出,多基地相参雷达的一个重要优势:在已知干扰源干扰方向的前提下,可实现主波束内干扰信号的对消而不抑制目标回波。倘若空间有多个干扰方向未知的干扰源,由于未知因素的存在,将会给接收站之间的联合信息处理造成影响,干扰抑制性能还有待研究。
结合以上分析,本文着重研究天线主瓣内存在多个干扰源,且干扰方向未知时,多基地相参雷达抗主瓣干扰的性能。
1 目标回波信号模型
假设多基地雷达由一个发射站与m个接收站组成,各接收站之间基线长度的布设,影响着目标回波信号在站间输入端的相关性。倘若基线长度满足站间弱相关的条件,当发射信号照射目标时,考虑到实际接收信号的幅度有效值与初相位的随机性,可将第i个接收站的目标回波信号可表示为
Si(t)=Asis0(t-Δtsi)exp{j[(ω0+Δωsi)(t-Δtsi)+φsi]},
(1)
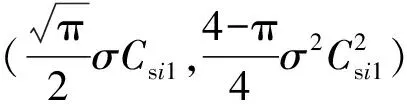
2 干扰信号模型
由于干扰信号的类噪声与复随机特点,其模型可通过互功率谱来建立。针对天线主瓣内存在多个方向未知干扰源的情况,模型的建立将主要分为2个步骤:①估计不同干扰源空间方位信息;②结合估计信息,建立干扰信号模型。
2.1 不同干扰源空间方位信息的估计
在估计干扰源空间方位方向信息时,考虑到多个干扰源空间角度相近,为了提升对干扰源的分辨性能,及时准确获知空中干扰源的数量,本文提出了一种改进的多重信号分类(multiple signal classification,MUSIC)算法来实现干扰源空间方位信息的估计,具体过程如下。
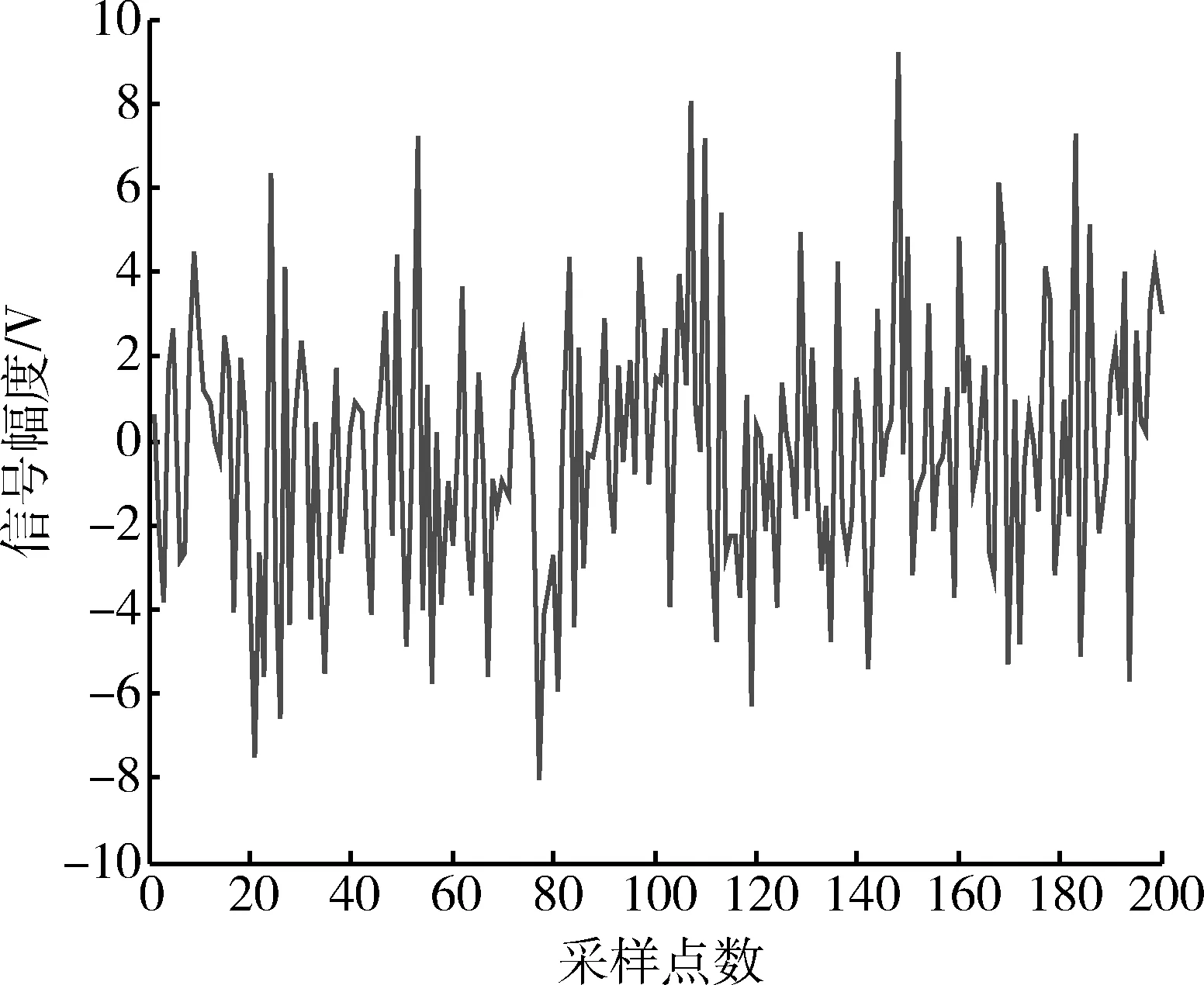
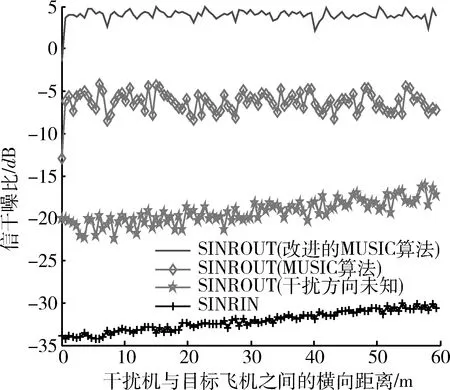
假设有m个接收站,空间存在p(p X=(x1,x2,…,xm)T=S+J+N, (2) 式中:S为m个接收站的目标回波信号矢量,S=(s1,s2,…,sm)T;J为p个干扰源产生的干扰信号矢量,J=(j1,j2,…,jp)T;N为不同接收站的内部噪声矢量。 (3) 式中:Q为快拍次数。 (4) 式中:Θj,Θsn分别为干扰子空间、信号与噪声子空间;Λj,Λsn分别为干扰对角阵、信号与噪声对角阵。 针对文献[10-11]中的相关内容,对MUSIC算法的空间谱表达式作出改进。改进的空间谱表达式为 (5) 式中:γ(α)为干扰的导向矢量;κ的表达式为 (6) 2.2 模型的建立 由于从天线主瓣进入接收机的干扰信号是一种类似噪声的复随机信号,因此可用互功率谱来反映干扰特性。则m个接收站输入端的干扰与噪声互功率谱矩阵[3-12]为 (7) 式中:Ψ为n×n矩阵,且对角线元素分别为各自接收站内部噪声的功率谱密度(power spectral density,PSD);Γk(w)为第k个干扰源归一化复包络PSD;Χk(w)为n×1矩阵,其第i(i=1,2,…,n)个元素为 (8) 假设空中有一架目标飞机正朝着地面多基地雷达系统匀速等高飞行,其初始位置同单基地雷达(transmitter and receiver,TR)雷达站距离为200 km,飞行高度10 km,飞行速度600 m/s。该飞机上携带有2架小型干扰机,在某一时刻干扰机均被投放,进行随队掩护飞行,并对TR雷达站形成了主瓣干扰。已知2架干扰机的飞行方向略微偏离目标飞机,偏离度分别为0.1°与0.6°,其他飞行参数同目标飞机一致。仿真从干扰机被投放时刻开始,记该时刻t=0,至偏角较大的干扰机与目标飞机横向距离为60 m时结束。已知发射站发射脉冲信号,信号载频为1 GHz,采样频率为5 GHz,数据预处理延迟通道个数为5。 结合文献[3]中提到的主瓣干扰对消算法,设定多基地雷达系统为TR-R2型,3个接收站呈等角环行部署方式,且两两之间的基线长度均为25 km。仿真分别利用经典MUSIC算法与改进的MUSIC算法进行干扰源方位信息估计,得到不同的干扰模型,进而研究其对干扰抑制的影响。具体仿真结果如图1~5所示。 图1 干扰对消前的输出信号波形Fig.1 Output signal wave before interference cancellation 图2 干扰方向未知时的对消效果Fig.2 Cancellation effect in unknown interference direction 图3 采用MUSIC算法估计方位后的对消效果Fig.3 Cancellation effect after estimation azimuth by using MUSIC algorithm 图4 采用改进MUSIC算法估计方位后的对消效果 Fig.4 Cancellation effect after estimation azimuth by using improved MUSIC algorithm 图5 输入与输出SINR的比较Fig.5 Comparison between input and output SINR 分析并比较图1~5可得以下结论:①干扰对消前,目标回波信号被干扰信号完全淹没,且干扰信号幅度普遍超出-2~2 V的范围;②干扰方位未知情况下进行干扰相消,目标回波信号依然被干扰信号淹没,但干扰信号幅度有所下降,幅度范围在-0.09~0.03 V之间;③若先采用MUSIC算法估计方向,然后再进行干扰对消,目标回波信号显现,峰值幅度约为0.016 V,而采用改进MUSIC算法处理后,峰值幅度可达到0.05 V;④通过对输入与输出信号与干扰加噪声比(signal to interference plus noise ratio,SINR)的比较可知,将改进的MUSIC算法与干扰相消相结合,SINR改善效果最优,改善量约为25~30 dB。 本文意在研究多干扰源环境下多基地雷达抑制主瓣干扰的性能,在干扰方向未知时,首先通过提出一种改进的MUSIC算法估计干扰方位信息,重新建立干扰模型,然后进行干扰相消。仿真结果表明,经过以上处理后,无论从干扰对消效果,还是从输出SINR改善情况分析,该方法均是有效的,具有一定应用价值。 [1] DAI Huan-yao, WANG Xue-song, LIU Yong, et al. Novel Research on Mainlobe Jamming Polarization Suppression Technology [J]. Science China, 2012, 55(2): 368-369. [2] 刘柏君. 高频雷达中基于多频信号的波束形成方法研究[D].哈尔滨:哈尔滨工业大学, 2011. LIU Bai-jun. Research on Beamforming Based on Multi-Frequency Signals in HF Radar [D].Harbin: Harbin Institute of Technology, 2011. [3] Victor S Chernyak.Fundamentals of Multisite Radar Systems:Multistatic Radars and Multiradar Systems[M]. Beijing:Publishing House of Elsctronics Industry,2011:70-222. [4] 司伟建,蓝晓宇,刘学. 提高二维DOA估计分辨率的改进MUSIC算法[J]. 西安电子科技大学学报:自然科学版, 2012,39(2):139-140. SI Wei-jian, LAN Xiao-yu, LIU Xue. Modified MUSIC Algorithm for Improving the Resolution of 2-D Direction of Arrival Estimation. Journal of Xidian University:Natural Science ed, 2012,39(2):139-140. [5] 梁国龙,张锴,范展,等. 单矢量传感器MUSIC算法的DOA估计及性能评价[J]. 哈尔滨工程大学学报, 2012,33(1):31-32. LIANG Guo-long, ZHANG Kai, FAN Zhan, et al. Performance Evaluation of DOA Estimation Using A Single Acoustic Vector-Sensor Based on An Improved MUSIC Algorithm[J]. Journal of Harbin Engineering University, 2012, 33(1): 31-32. [6] AKKAR S,GHARSALLAH A. Reactance Domains Unitary MUSIC Algorithms Based on Real-Valued Orthogonal Decomposition for Electronically Steerable Parasitic Array Radiator Antennas[J]. IET Microwaves, Antennas & Propagation, 2012,6(2):226-227. [7] HE Jin,SWAMY M N S,OMAIR AHMAD M. Efficient Application of MUSIC Algorithm Under the Coexistence of Far-Field and Near-Field Sources[J]. IEEE Transactions on Signal Processing, 2012,60(4):2067-2069. [8] 谢白玉, 赵鹏. 基于改进MUSIC算法的信号DOA估计[J]. 微计算机信息, 2011, 27(11): 162-163. XIE Bai-yu, ZHAO Peng. A Method of DOA Estimation by Modified MUSIC Algorithm[J]. Microcomputer Information, 2011, 27(11): 162-163. [9] 王阳, 鲁祖坤, 石宇, 等. MIMO雷达中基于Cyclic-Music算法的DOA估计[J]. 中国雷达, 2012, 30(4): 30-31. WANG Yang, LU Zu-kun, SHI Yu, et al. DOA Estimation Based on Cyclic-Music Algorithm in MIMO Radar[J]. China Radar, 2012, 30(4): 30-31. [10] 秦润东,李永彤,于清津. 基于实值分解技术的Root-MUSIC 算法[J]. 海上靶场学术, 2012(9):66-67. QIN Rui-dong, LI Yong-tong, YU Qing-jin. Root-MUSIC Algorithm Based on Real-Valued Decomposition Technique[J]. Sea Shooting Research, 2012(9):66-67. [11] 刘志刚, 汪晋宽, 王福利. 基于实值分解技术的循环root-MUSIC 算法[J]. 系统仿真学报, 2006, 18(9): 2438-2442. LIU Zhi-gang, WANG Jin-kuan, WANG Fu-li. Cyclic root-MUSIC Algorithm Based on Real-Valued Decomposition[J]. Journal of System Simulation, 2006, 18(9): 2438-2442. [12] KONG Ling-jiang, YANG Mei, ZHAO Bin. Adaptive Detection for Shared-Spectrum Multistatic Radar in Gaussian Clutter[C]∥ 2012 IEEE Radar Conference, Atlanta, May 7, 2012:310-31. Main-Lobe Jamming Suppression Method in the Presence of Many Disturbance Sources WANG Qiang,ZHANG Yong-shun,SI Wen-tao (AFEU,Air and Missile Defense School,Shaanxi Xi’an 710051, China) Aiming at, a kind of new method is proposed to solve the problem of bad jamming suppression effect on direction of the unknown space interference sources Firstly, it estimates the source azimuth information using improved multiple signal classification (MUSIC) algorithm and establishes interference model anew, secondly, makes the joint interference cancellation among different receivers. Combing the simulation experiment, we can know the signal peak amplitude reach 0.05 V and the output signal to interference plus noise ratio (SINR) improves about 25~30 dB through above two step. The experimental result states this method is effective. many disturbance sources; multistatic radar; main-lobe cancellation 2013-11-27; 2014-06-29 陕西省自然科学基金资助项目(2010JQ8007) 王强(1989-),男,陕西三原人。硕士生,主要从事多基地雷达信号处理研究。 通信地址:710051 陕西省西安市长乐东路甲字一号防空反导学院研2队 E-mail:1019611183@qq.com 10.3969/j.issn.1009-086x.2015.03.006 TN973;TN953+.7 A 1009-086X(2015)-03-0035-04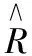
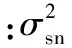

3 仿真实验与分析



4 结束语
