基于改进遗传算法的雷达网优化部署方法研究*
2015-05-05甘刚李桂祥左治方朱新权
甘刚,李桂祥,左治方,朱新权
(空军预警学院,湖北 武汉 430019)
基于改进遗传算法的雷达网优化部署方法研究*
甘刚,李桂祥,左治方,朱新权
(空军预警学院,湖北 武汉 430019)
雷达网的综合效能直接影响着作战能力,研究雷达网的优化部署旨在提高其综合效能。针对雷达网优化部署涉及的影响因素众多、难以综合考虑的问题,从雷达网的覆盖率、重叠度 、“四抗”能力以及费效比方面对雷达网优化部署进行约束,通过定量分析研究,并且利用改进的遗传算法加以实现,给出一种雷达网优化部署的可行办法,仿真结果表明了优化部署的可行性。
雷达网;综合效能;影响因素;优化部署;约束;遗传算法
0 引言
防空预警系统经过几十年的建设和部署,基本形成了覆盖全国的防空预警雷达网,但是面对日益复杂的目标环境、不断复杂的电子战环境和日益恶劣的战场环境存在面临隐身、低空、小型目标来袭,防空预警网络存在“看不见、看不远”的问题,面对高空、高速火力打击,防空预警网络存在“看不高、跟不上”的问题,面对全时域、全空域、全频域、高强度的电子干扰,防空预警网络存在干扰后的“看不远、识别难”的问题,面对多手段、高效能的反辐射攻击,防空预警网络可能存在“生存难”等问题。
而且遗憾的是,由于装备制造工艺要求跟不上、装备部署受地形限制、缺乏完全发挥装备性能的技术骨干以及对防空预警网络构建的综合性研究不够等原因,致使防空预警雷达网的效益不高,主要表现在:
(1) 责任区有些区域覆盖不到、重叠不够,有些区域覆盖冗余;
(2) 雷达网对抗综合性电磁干扰、隐身目标、低空/超低空突防以及反辐射导弹能力较弱;
(3) 雷达网雷达数量较多,费效比降低等。
由此可见,雷达网的优化部署需要考虑的约束条件多,同时任务要求高,可以定性为非线性、多约束、多目标的复杂优化问题,但是雷达网优化部署的研究意义不言而喻,而且亟需更为可行的指导理论。本文即是从上述不足出发,通过建模仿真对雷达网的优化部署进行研究。
目前的相关研究工作一是研究的雷达网包含装备数量较少[1-3],应用性不强;二是研究雷达网单个影响因素的多,综合把握的少[4-6],难以推广;三是受人工智能算法本身固有的缺点影响[7-10],研究结果有待系统评估检验。本文在上述研究以及文献[11]的研究基础之上,进一步深化雷达网的优化部署,力争对提高雷达网的综合性研究做出贡献。
1 优化部署问题分析
雷达网是指2部(含)以上架设于不同地点或不同高度上的雷达构成的防空网,它通过情报站信息融合,使得其综合性能或覆盖空域优于单部雷达[12]。不同体制、不同波段的雷达装备因其工作原理和一些技术参数等方面的不同,它们的装备性能各有所长和不足,雷达网的优化部署即是科学合理部署,通过单个雷达性能的优势互补使得构成的防空网综合性能更优。
1.1 雷达网优化部署原则
雷达网的优化部署应该按照以下原则进行[9,13]:
(1) 雷达装备的部署最重要是依据上级指挥决策者对责任区的部署意图和敌我兵力部署情况统一布局。
(2) 在雷达装备数量最优(最合理)的条件下,要满足责任区的覆盖要求,即探测范围尽可能大,此时雷达网的费效比也最大。
(3) 雷达网对空域的覆盖不仅包括平面的覆盖还包括高度的覆盖,而且重要高度层的目标区域要求达到一定的重叠度。
(4) 雷达网中的雷达工作频段要尽可能宽,从而达到抗干扰和抗隐身目标的目的,但是为避免网内同频干扰,各雷达之间的距离要计算好;同时可以在适当的地理位置架设无源雷达等来提高雷达网的抗干扰性能。
(5) 雷达网的部署要重视低空补盲,防止低空/超低空突防,除了常规低空补盲雷达之外,可以在适当的地理位置架设气球载雷达等进行低空补盲。
(6) 确保雷达网有较好的抗ARM能力以及一定的机动性,这也是提高雷达网生存能力的体现之一。
1.2 雷达网优化部署约束条件及模型
雷达网的优化部署约束条件实际上是对部署原则的数学描述,本文主要考虑以下几个约束条件。
(1) 平均高度层覆盖系数
便于建立模型,将雷达网的覆盖空域等效为M个高度层,每个高度层覆盖面积看做半径为Rmax的圆面积。这里的“覆盖”是指雷达网对目标的探测概率P不小于规定的概率值Pdo,即P≥Pdo。将高度层覆盖责任区网格化,根据式(1)对网格进行赋值di,i≤N,即每当一部雷达探测到目标一次,目标所在的网格赋值变1,同一目标同时被i部雷达探测到时,网格赋值相应叠加i,i≤N次。
(1)
赋值效果如图1所示。

图1 责任区赋值效果图Fig.1 Effect of assignment in area
高度层覆盖系数ρ可表示为
ρ=(n1+n2+…+ni)/n0,
(2)
式中:ni为覆盖i次的格数;n0为责任区网格总数。
平均高度层覆盖系数可表示为
(3)

(2) 重叠度系数
重叠度系数建模思想和平均高度层覆盖系数的建模思想一致,区别在于重叠度要求雷达覆盖的次数多一些。因此,重叠度可以表示为
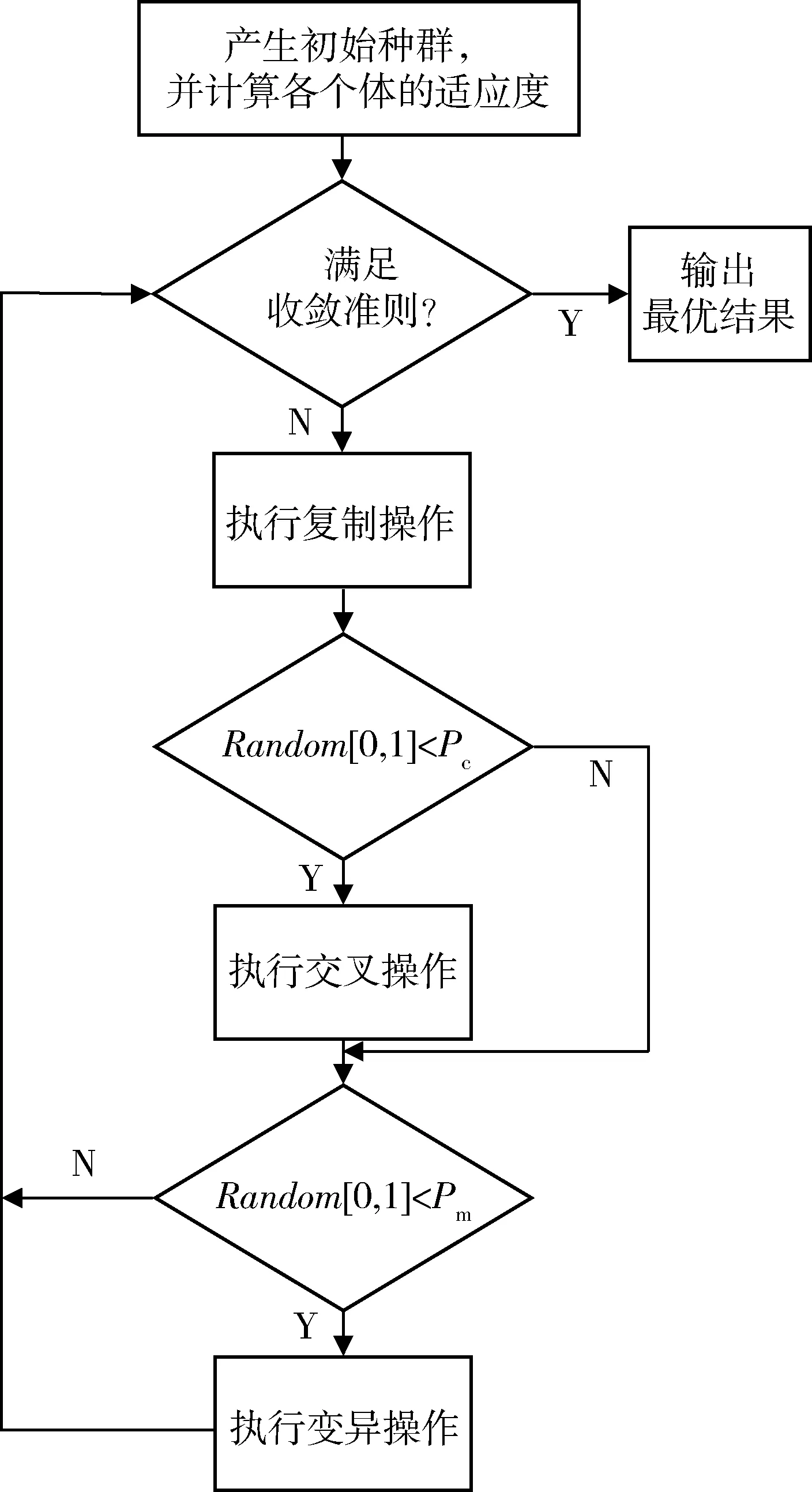
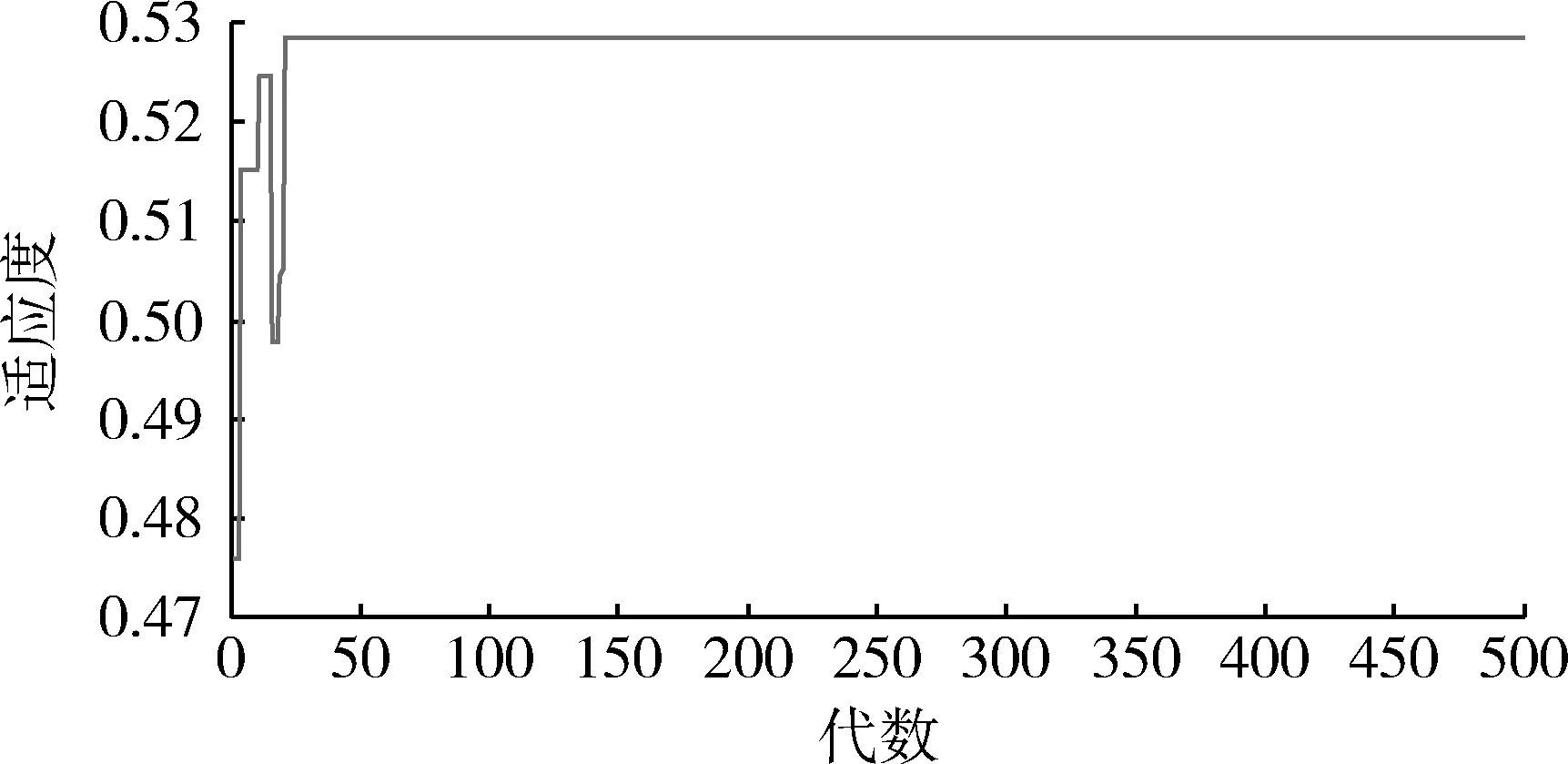
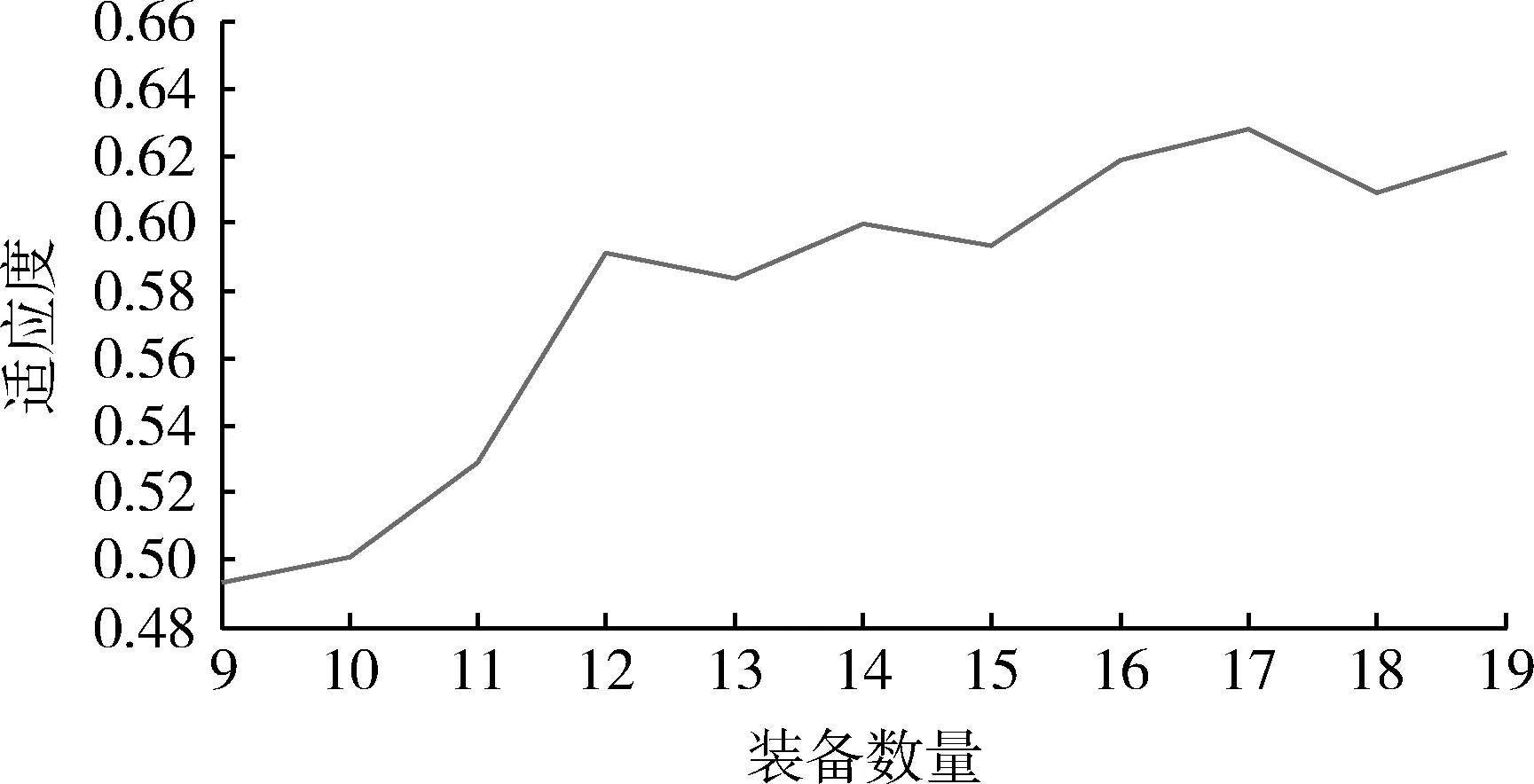
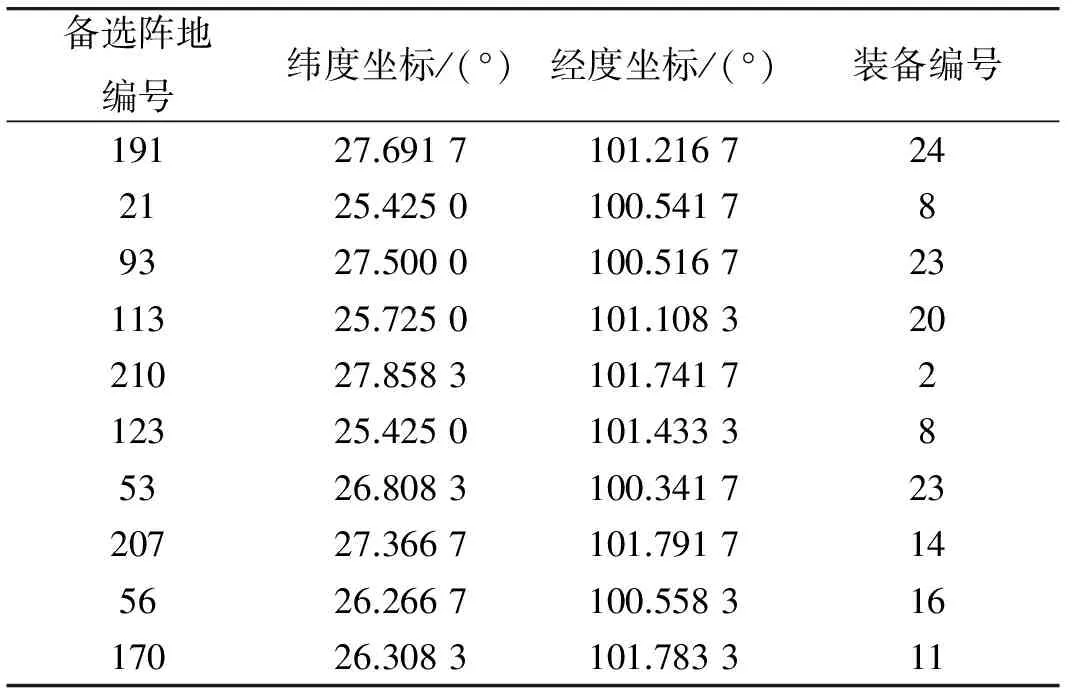
φj=(nj+nj+1+…+ni)/n0,j (4) 式中:j为重叠次数,一般j≤3。 (3) 抗干扰能力系数[14] 雷达网抗干扰除了雷达固有的技术措施外,和组网带来的频域重叠、极化覆盖以及信号种类等附加因子紧密相关,尤其是频域抗干扰,是目前应用最多、最有效的措施。 1) 频域重叠 频域重叠是指网内各雷达带宽的重叠,雷达网的抗干扰能力与其带宽呈正相关,因此雷达网的带宽要尽可能的大。假设由N部雷达组成的雷达网中第部雷达的带宽为Δfi,i=1,2,…,N,共有n部雷达带宽有重叠,重叠带宽为Δfj,j=1,2,…,n,则频域重叠系数η可表示为 (5) 2) 极化覆盖 雷达网中的极化类型越多,抗干扰能力就越强,用极化覆盖系数表征雷达网极化类型的多少。假设由N部雷达组成的雷达网中有n种极化类型,则极化覆盖系数J可表示为 J=n/N. (6) 3) 信号种类 雷达网中的信号种类越多,抗干扰能力就越强,用信号种类参数表征雷达网信号种类的多少。假设由N部雷达组成的雷达网中有n种信号类型,则信号种类参数S可表示为 S=n/N. (7) 综上,抗干扰能力系数AJ通过加权可表示为 AJ=ω1η+ω2J+ω3S, (8) (4) 抗隐身能力系数 雷达网抗隐身目标的措施主要包括与雷达本身相关的平均发射功率等,以及利用隐身目标的频域窗口、极化域窗口和空域窗口等[14]。为保证雷达网综合性能各影响因素的独立性,极化形式多样性和频率域在抗干扰模型中已经考虑,故此处不作考虑;空域窗口是针对已知来袭方向,在来袭方向未知的情况下考虑空域抗隐身意义不大,因此,抗隐身模型中主要突出功率抗隐身。 单部雷达的抗隐身能力(AS)i可以表示为 (AS)i=PtGtTτ/F, (9) 式中:Pt为雷达平均发射功率;Gt为天线增益;T和τ分别为目标驻留时间和脉冲宽度;F为噪声系数。 假设(AS)max为雷达网中单部雷达抗隐身能力得最大值,则由N部雷达组成的雷达网抗隐身能力系数AS可以表示为 (10) 即雷达网中各雷达的平均抗隐身能力值和最大抗隐身能力值之比。 (5) 抗低空突防能力系数 目前雷达网抗低空/超低空突防主要是通过技术实现提高雷达的杂波中可见度,或者使用低空补盲雷达。杂波中可见度为雷达的固有参数,本文只考虑低空补盲雷达数量的增加对雷达网抗低空突防能力的影响。假设由N部雷达组成的雷达网中有n部低空补盲雷达,则抗低空突防能力系数可表示为 AL=n/N. (11) (6) 抗反辐射导弹(ARM)能力系数 雷达网抗ARM技术上主要是通过诱偏系统,实际操作中除了设置诱饵,加装ARM告警系统,一般利用米波雷达实现抗ARM。假设由N部雷达组成的雷达网中有n部米波雷达,则抗ARM系数可表示为 AA=n/N. (12) 1.3 雷达网综合性能模型 雷达网的综合性能可以通过1.2节的约束条件来系统性表征,即: F=ω1ρ+ω2φj+ω3(A,J)+ ω4(AS)+ω5(AL)+ω6(AA) (13) 2.1 遗传算法概述 遗传算法(generation algorithm,GA)是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法,其原理是生物通过选择、遗传和变异等维持优秀基因并促使群体进化。GA具有群体并行搜索功能、不容易陷入局部收敛等突出优点[15]。 GA主要步骤包括:编码、初始化、设置参数、确定适应度函数、选择、交叉以及变异等遗传操作。编码一般常用的有二值编码、多值编码以及实数编码等;选择操作又称复制,目的是保留染色体中的优秀基因,常用的有轮盘赌选择和比例复制;交叉操作是两个染色体重组新的个体,是GA的主要操作,通过交叉操作使得GA搜索效率飞速提升,常用的有算术交叉、单点交叉等;变异操作是某个染色体的某个基因发生突变,目的是增加个体多样性,同时提高局部搜索能力使得GA加速向最优解收敛。常用的变异有常规位变异和均匀变异等。 2.2 遗传算法流程 在了解GA的主要步骤之后,GA的流程图(图2)表示如下,共有7个步骤: 图2 GA流程图Fig.2 Flow chart of GA Step 1 编码,制定收敛准则,确定适应度函数,设置好GA参数; Step 2 初始化种群,计算每一个体适应度,并判断适应度最大的个体对应的解是否满足收敛准则,是则输出结果,否则进入Step 3; Step 3 根据适应度,按照一定方式进行复制操作; Step 4 在闭区间[0,1]上随机选定一个随机数r1和交叉概率Pc进行比较,r1 Step 5 按交叉概率进行交叉操作; Step 6 在闭区间[0,1]上随机选定一个随机数r2和变异概率Pm进行比较,r2 Step 7 按交叉概率Pm进行遗传操作,然后返回Step 2。 2.3 改进遗传算法设计 对于雷达网优化部署这一复杂问题,本文进行了以下改进算法设计,具体如下: (1) 编码 文献[11]提出一种阵地选择方法,给据此方法选择出来的备选阵地编号,同时给现有装备进行编号,则染色体前半部分基因为备选阵地编号,后半部分基因为装备编号,编码成功后备选阵地编号和装备编号一一对应。二值编码致使染色体过长,并且解码复杂,因此选择实数编码。 (2) 初始化 假设雷达网装备数量为N,则染色体长度为2N,初始种群建议[16]取3N。雷达网装备数量和责任区面积有一定的关系,利用放大缩小的思想,大致可以确定两者关系如下: (14) (3) 确定适应度函数 适应度函数采用雷达网综合性能函数。 (4) 制定收敛准则 采用混合决策型收敛准则,即规定GA运行到指定代数前已经收敛,收敛则立即停止,否则运行到指定代数停止。 (5) 确定遗传算子 选择操作采用比例复制;交叉操作选择适合实数编码的算术交叉,交叉概率为Pc∈[0,1];变异操作采取适合实数编码的均匀变异,变异概率为Pm∈[0,0.1]。 (6)结合实际 考虑选择费效比最优的雷达装备部署方案,雷达装备数量分别取(N-1)和(N+1)重复步骤(2)~(5),并最终对比3次分别得到的最优部署方案,选择费效比优的输出保存。 改进的GA优点体现在:一是编码方式简单易懂又符合站点和装备一一对应的部署实质,且有效避免了染色体过长带来的解码复杂以及运算量大等问题;二是混合决策收敛准则符合雷达网构建的思想,即满足任务要求的性能,次之也要尽可能地逼近,且有效减少了GA运行次数;三是考虑费效比,使GA码长可变,利于得到最优解。 假设某责任区主要负责200 m高空的警戒任务,防区面积为60 000 km2,根据公式(14)可大致求出需要10~19部装备,本文从费效比角度,选择10部装备进行仿真。从备选阵地库中选择10个站点,从装备数据库中选择10部性能不同的装备进行优化部署,每一个装备编号都代表数据库中的固定装备。要求警戒系数F≥0.5。则应用改进的遗传算法进行仿真,装备数量N=10,则染色体长度为20,初始种群为30;交叉概率取Pc=0.8,变异概率取Pm=0.05,分别对9,10,11部装备进行GA优化部署,各运行500次,如果未收敛的话即停止,仿真分析如下: (1) 仿真条件 装备数量根据式(14)可得大概值,本文取9~11部;警戒系数至少大于0.5;权重系数的确定要突出抗低空突防能力,因此,结合防区任务分别取相应的典型值为:ω1=0.3;ω2=0.1;ω3=0.1;ω4=0.05;ω5=0.4;ω6=0.05。 (2) 仿真数据 表1为当装备数量分别为9,10,11,优化代数为200,300,500时,得到的部署综合性能。 表1 不同代别、不同装备数量时的综合性能Table 1 Performances of radar-net of different time and different number of equipment 9~11部雷达组成的雷达网性能仿真图分别如图3~5所示。 图3 9部装备组成的雷达网性能Fig.3 Performance of radar-net of 9 equipments 图4 10部装备组成的雷达网性能Fig.4 Performance of radar-net of 10 equipments 图5 11部装备组成的雷达网性能Fig.5 Performances of radar-net of 11 equipments 最后,对由不同装备数量构成的雷达网的综合性能进行仿真,即不同染色体对应的适应度,通过描点可得,如图6所示。 图6 不同装备数量下的雷达网性能Fig.6 Performances of radar-net of different number of equipment 由表1和图6可得出结论,对于责任区面积一定时: 1) 雷达网装备数量和雷达网的综合性能呈正相关; 2) 每一个责任区都存在一个最适宜的装备数量Nmax构成的雷达网,之前随着装备数量Nmax的增加,F增加较快;Nmax之后随着装备数量N的增加,F增加不明显。 本例中,从满足任务要求和费效比角度出发,选择10部装备构成的雷达部署方案即可。10部装备构成的雷达网详细部署情况见表2。 表2 10部装备部署情况表Table 2 Deployment situation of radar-net of 10 equipments 在表2的基础上,对应查找装备序列的编号,即可得到实际的装备情况,这和GA中的解码是类似的。 本文针对雷达网优化部署问题从覆盖率、重叠度以及“四抗”能力上进行约束分析,并建模仿真得到了雷达网优化结果,证明了本文提出方法的可行性,得出了每个责任区都存在一个最适宜的装备数量构成的雷达网满足任务需求,而且给出了确定最适宜装备数量的模型,对部队指挥决策有一定的指导意义。有一点需要深入探讨的是各约束条件之间的独立性处理的不够完善,以及因此对雷达网性能带来的影响值得进一步研究。 [1] 高尚.两部雷达最佳部署问题研究[J].数学的实践与认识,1999,29(3):52-55. GAO Shang.Research on Optimal Deploy Problem of Two Sets of Radar[J].Mathematics in Practice and Theory, 1999,29(3):52-55. [2] 孙亮.两部雷达部署的研究[J].数学的实践与认识,2003,33(4):22-25. SUN Liang. Research on Optimal Deploy of Two Sets of Radar[J].Mathematics in Practice and Theory, 2003,33(4):22-25. [3] 肖华勇,彭国华.多部雷达最佳部署的遗传算法研究[J].数学的实践与认识, 2002,32(6):979-982. XIAO Hua-yong,PENG Guo-hua. Research on Optimal Deploy Problem of Multiple Sets of Radar with Genetic Algorithm [J].Mathematics in Practice and Theory, 2002,32(6):979-982. [4] 李侠,蔡万勇,花良发,等.责任区雷达组网系统抗干扰优化部署算法[J].系统工程与电子技术,2007,29(8):1254-1257. LI Xia,CAI Wan-yong,HUA Liang-fa. Algorithms of Anti-Jamming Optimized Arrangement for Radarnetworking System with Warning Area [J]. Systems Engineering and Electronics, 2007,29(8):1254-1257. [5] 徐庆民,姚佩阳,陈元元,等.基于微分进化算法的区域雷达网抗干扰优化方法[J].现代防御技术,2009,37(3):105-108. XU Qing-min, YAO Pei-yang,CHEN Yuan-yuan.Approach to Regional Radar Net Anti-Jamming Optimization Based on Differential Evolution Algorithm [J]. Modern Defense Technology, 2009,37(3):105-108. [6] 祝长英, 李成海,卢盈齐.雷达组网反隐身的优化布站问题研究[J]. 电光与控制,2009,16(4):69-71. ZHU Chang-ying, LI Cheng-hai, LU Ying-qi. Research on Optina1 Deployment of NettedRadar for Detecting Stealth Target [J]. Electronics Optics & Control, 2009,16(4):69-71. [7] 王中杰,李侠,周启明,等.基于多约束条件遗传算法的雷达网优化部署[J].系统工程与电子技术,2008,30(2):265-268. WANG Zhong-jie,LI Xia,ZHOU Qi-ming.Optimal Deployment of Radar Network Based on Multi-Constrained GA[J].Systems Engineering and Electronics, 2008,30(2):265-268. [8] 王薇,韩传久.基于蚁群算法的雷达组网优化布站方法[J].微计算机信息,2007,23(10): 13-16. WANG Wei,HAN Chuan-jiu.Research on Optimal Disposition of Sets of Radar Based on Ant Colony Algorithm[J].Microcomputer Information, 2007,23(10): 13-16. [9] 何庆元.基于粒子群优化算法的雷达网优化布站研究[D].桂林:桂林电子科技大学,2006. HE Qing-yuan.Researching on Optimize Embattle of Radar Netting Based on Particle[D].Guilin:Guilin University of Electronic Science and Technology,2006. [10] 张培珍,杨根源,武志东,等.模拟退火算法在雷达网优化部署中的应用[J].现代防御技术,2010,38(6):18-21. ZHANG Pei-zhen,YANG Gen-yuan,WU Zhi-dong,et al. Application of Simulated Annealing Algorithm on Radar Netting Optimal Disposition[J].Modern defence technology, 2010,38(6):18-19. [11] 甘刚,李桂祥,左治方.基于DEM的米波雷达阵地选择方法研究[J].空军预警学院学报,2014,28(3):187-188. GAN Gang,LI Gui-xiang,ZUO Zhi-fang. Research on Selection of Meter-Wave Radar Site Base on DEM[J].Journal of Air Force Early Warning Academy, 2014,28(3):187-188. [12] 徐锦起,李侠,朱建平,等.地面对空监视雷达网体系结构研究[J].现代防御技术,2003,31(4):35-36. XU Jin-qi,LI Xia,ZHU Jian-ping. Research on the System Structure of Surveillance Radar Net [J].Modern Deffence Technology,2003,31(4):35-36. [13] 蔡婧.雷达组网系统的优化组网方法研究[D].镇江:江苏科技大学,2010:12-14. CAI Jing. Study on the Method of Radar Networking System Optimization of Network[D].Zhenjiang:Jiangsu University of Science and Technology, 2010:12-14. [14] 陈永光,李修和,沈阳.组网雷达作战能力分析与评估[M].北京:国防工业出版社,2006:28-174. CHEN Yong-guang,LI Xiu-he,SHEN Yang.Analysis and Evaluation of Netted Radar Operational Capability[M].Beijing:National Defense Industry Press, 2006:28-174. [15] 王凌.智能优化算法及其应用[M].北京:清华大学出版社,2001:36-38. WANG Ling.Intelligent Optimization Algorithms with Applications[M].Beijing:Tsinghua University Press, 2001:36-38. [16] 吕晋君.遗传算法的改进及其在优化上的应用研究[D].太原:太原理工大学,2010. LÜ Jin-jun. Studies on Improvement of Genetic Algorithmand its Applications in Optimization [D]. Taiyuan:Taiyuan University of Technology,2010. Study on Radar-Net Deployment Optimization Method Based on Improved Genetic Algorithm GAN Gang,LI Gui-xiang,ZUO Zhi-fang,ZHU Xin-quan (Air Force Early Warning Academy,Hubei Wuhan 430019, China) The comprehensive efficiency of radar network directly affects its operational capability, and to study radar-net deployment optimization aims to increase the comprehensive efficiency. For the problem of radar-net deployment optimization involves many influencing factors and complexity, radar-net deployment optimization is constrained from coverage rate, degree of overlapping, “Four Anti-threaten ability” and cost-benefit ratio and the optimization is achieved through the method of quantitative analysis and improved genetic algorithm. A feasible measure of the radar-net deployment optimization is proposed, and simulation and test results illustrate its feasibility. radar net; comprehensive efficiency;influence;deployment optimization;constrain; genetic Algorithm 2014-09-30; 2015-01-14 甘刚(1989-),男,陕西宝鸡人。硕士生,研究方向为防空预警相关。 通信地址:430019 湖北省武汉市江岸区黄浦大街288号 E-mail:18653324504@163.com 10.3969/j.issn.1009-086x.2015.04.007 TN95;TP301.6 A 1009-086X(2015)-04-0036-07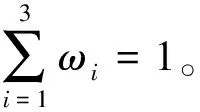
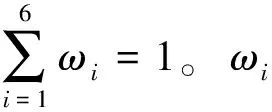
2 优化部署算法设计
3 优化部署实例仿真



4 结束语
