吊挂刚度对车体及牵引变压器振动指标的影响分析

屈晶晶， 张立民

(西南交通大学 牵引动力国家重点实验室， 四川成都 610031)

吊挂刚度对车体及牵引变压器振动指标的影响分析

屈晶晶， 张立民

(西南交通大学 牵引动力国家重点实验室， 四川成都 610031)

介绍了用于动车组车体和牵引变压器振动评定的两种指标，建立了车体-变压器有限元模型。改变车体与牵引变压器之间的连接参数——吊挂刚度，并在变压器及车体空簧处施加不同速度级下的对应实测振动信号，提取车体端部及变压器上部和底部振动响应，计算车体平稳性及变压器振动烈度。结果表明：当在350 km/h速度级下时，车体平稳性随着牵引变压器垂向吊挂刚度的增大而减小，在385 km/h速度级下时平稳性则随着垂向吊挂刚度的增大先减小后增大；车体平稳性随着横向吊挂刚度的增大则不发生明显改变；牵引变压器的振动烈度随着其吊挂刚度的增大也不发生明显改变。可得结论：牵引变压器自身的振动受吊挂刚度变化的影响较小；牵引变压器的垂向吊挂刚度较横向吊挂刚度对车体平稳性指标的影响程度更为显著。

振动与波； 车体-变压器； 吊挂刚度； 平稳性； 振动烈度

随着科技的不断进步，高速列车在我国迅猛发展。速度的提升可谓是高速列车发展最为显著的一个特征——从最初引进速度200 km/h的高速列车技术，到如今利用自主科技研制速度350,380 km/h的“和谐号”动车组[1]。速度的飞跃代表了我国高速列车科研与应用的雄厚实力，同时极大地方便了旅客的出行。然而高速列车运行中难以避免的振动，也随着速度的提升而加剧。动车组车体和牵引变压器之间通过吊挂连接，作为振动的重要参数，吊挂刚度对动车的运行安全性以及提速的影响不容小觑[2]，有必要对其进行分析，弥补当前研究的不足。由于目前实际研究的难度较大，因此先仿真研究动车组车体和牵引变压器在不同的吊挂刚度和激励工况下，其振动评定指标变化的规律，分析吊挂刚度对车体和牵引变压器振动的影响。这可以为动车组的减振设计、舒适度改进提供参考依据和研究基础，具有一定的应用意义。

1 振动评定指标

1.1 车体—变压器有限元模型建立

车体结构主要由底架、侧墙、车顶和端墙等4部分组成[3]。根据实际结构特点进行有限元建模，车体模型主要用壳单元对车体结构进行模拟，将牵引变压器视为一个质量块下挂于车体下方，其中牵引变压器与车体间弹性连接采用弹簧单元(COMBIN14)进行模拟。系统总质量约为35.1 t，牵引变压器重6.5 t，车体和配重约28.6 t，计算模型包括126 953个节点，199 632个单元(196 940个壳单元，4个刚度矩阵单元-模拟橡胶垫，2 688个实体单元)ANSYS仿真模型如图1所示。

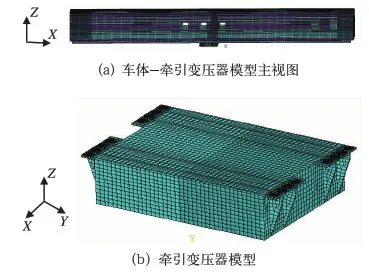
图1 ANSYS仿真模型图

1.2 平稳性指标

根据国家标准GB 5599-85《铁道车辆动力学性能评定和试验鉴定规范》(以下称为“规范”)规定，车体的振动评定采用平稳性指标，引用德国Sperling的平稳性指标的基本思想，计算公式为[4]:

(1)

式中W为平稳性指标；A为振动加速度,g；f为振动频率,Hz；F(f)为频率修正系数，由大量试验统计得出，见表1。

表1 频率修正系数

评定平稳性的等级分为3级，如表2所示。

表2 客车平稳性指标等级

根据“规范”，测点应选择在车体内部地板上两轮对中心连线中点前后各1 000 mm的位置处，一共4个测点，依次命名为测点1、测点2、测点3和测点4，如图2所示。

图2 车体平稳性的测点位置

1.3 振动烈度

当牵引变压器产生振动时，以变压器的振动烈度作为振动评定指标值。按照GB 5913-86《柴油机车车内设备机械振动烈度的评定方法》的规定，振动烈度是指设备在一定工况条件下，在选定的位置上按不同方向(一般是沿纵向、横向、垂向3个方向)测量出振动速度的有效值，利用矢量合成，计算出机械振动速度的均方根值，符号为vrms，单位为mm/s[5]。

机械振动烈度的基本计算公式为：

(2)

式中vx为选定位置(测点)上纵向振动速度均方根值,mm/s；vy为选定位置(测点)上横向振动速度均方根值,mm/s；vz为选定位置(测点)上垂向振动速度均方根值,mm/s；Nx为纵向测点数；Ny为横向测点数；Nz为垂向测点数。

振动烈度评定中的机械设备一般分为6大类，见表3。

第1类到第4类机械设备的振动烈度评价标准，见表4。

根据牵引变压器实际工作条件的特殊性以及牵引变压器要求坚固的机械结构、耐振动和冲击等自身特点，此处采用比较保守的判定方法，将其列为第一类机器进行振动评定。

针对变压器振动特点将测点放置于变压器和车体连接的4点处以及变压器底部的4点处，从上到下按逆时针方向依次命名为测点5、测点6、测点7、测点8、测点9、测点10、测点11、测点12，如图3所示。

表3 振动烈度评定中的机械设备分类

表4 常用机械设备的振动烈度等级表

图3 牵引变压器振动烈度的测点位置

2 仿真计算

2.1 激励点选取

设定每一种工况下车体和牵引变压器都将有信号激励。仿真所采用的原始信号为某线路试验中动车组分别在350 km/h和385 km/h速度级下的车体空簧处以及变压器4端隔振器处的实测振动加速度信号。因此，为提高仿真计算的精度和可靠性，激励点选取在车体的空气弹簧处和牵引变压器的4端隔振器处，如图4所示。

图4 车体和变压器激励加载

2.2 原始信号处理

由于ANSYS软件无加速度激励,因此将原始加速度信号经二次积分所得的位移信号作为激励进行加载。根据实测信号的特点，采取两种不同的信号处理方式。其中，牵引变压器的原始信号为明显规律的倍频信号，因此经快速傅里叶变换(FFT)以后取信号的前五阶主频，再二次积分得到变压器激励位移函数，将其加载在牵引变压器的4端隔振器处；车体空簧处的原始信号为随机信号，无明显规律，则直接将其进行二次积分得到位移信号，以矩阵的形式加载在模型的车体空簧处。

2.3 工况说明

由文献[6]可知，牵引变压器纵向吊挂刚度的变化对车体和变压器的振动评定无明显影响。因此本文同时改变牵引变压器垂向吊挂刚度和横向吊挂刚度，刚度变化设在40%～200%之间，表5为该模型中牵引变压器的原始吊挂刚度值，表6为仿真计算的刚度变化值。

表5 牵引变压器原始吊挂刚度值 MN/m

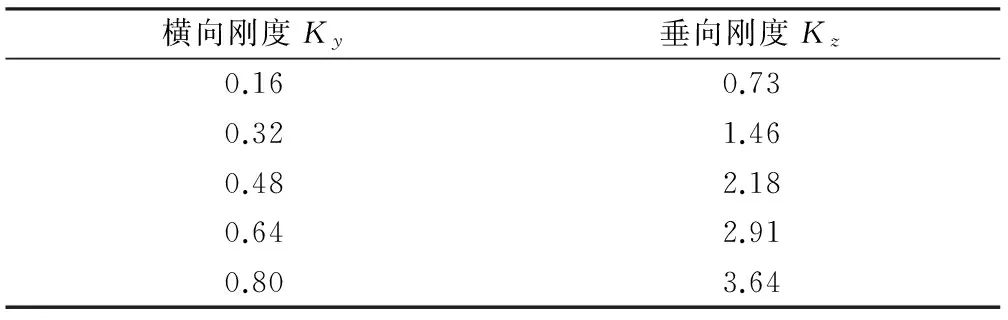
表6 仿真计算中牵引变压器的变刚度值 MN/m

对车体空簧处和牵引变压器同时进行激励，提取车体测点处的横向振动加速度、垂向振动加速度进行平稳性指标的计算，以及变压器测点处的纵向振动速度、横向振动速度、垂向振动速度进行振动烈度的计算。

3 结果分析

3.1 车体平稳性

以车体地板测点3的平稳性为例，不同速度级下平稳性与吊挂刚度的关系如图5～图8所示。

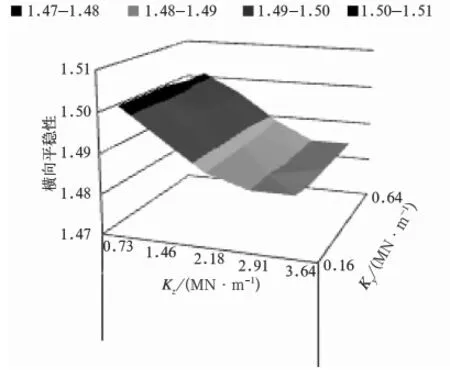
图5 横向平稳性随吊挂刚度变化图(v=350 km/h)

图6 垂向平稳性随吊挂刚度变化图(v=350 km/h)

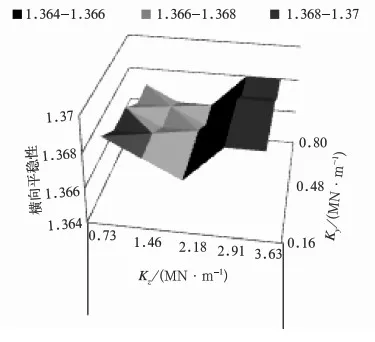
图7 横向平稳性随吊挂刚度变化图(v=385 km/h)

图8 垂向平稳性随吊挂刚度变化图(v=385 km/h)

由图5和图6可以看出，在350 km/h速度级时，平稳性随着牵引变压器垂向吊挂刚度Kz的增大逐渐减小，在Kz=3.64 MN/m时最小；而牵引变压器横向吊挂刚度的改变对平稳性的大小没有明显影响。

由图7和图8可以看出，在385 km/h速度级时，平稳性随着牵引变压器垂向吊挂刚度Kz的增大先减小后增大，在Kz=2.18 MN/m时最小；而牵引变压器横向吊挂刚度的改变同样对平稳性的大小没有明显影响。

3.2 牵引变压器的振动烈度

提取测点5、6、7、8、9、10、11、12的纵向、横向和垂向振动速度计算牵引变压器的振动烈度，如图9和图10所示。

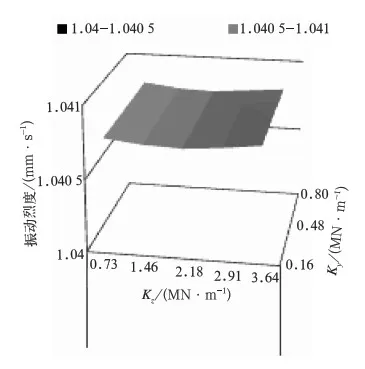
图9 振动烈度随吊挂刚度变化图(v=350 km/h)

由图9和图10可以看出，无论牵引变压器垂向、横向吊挂刚度如何改变，其振动烈度均无明显变化。

3.3 不同速度级下的振动评定指标的比较

除了牵引变压器的吊挂刚度变化会对振动评定指标产生影响以外，不同的运行速度对车体和牵引变压器的振动评定指标也会产生一定的影响。

图10 振动烈度随吊挂刚度变化图(v=385 km/h)

对于车体运行平稳性而言，同样以测点3为例，如图11和图12所示。

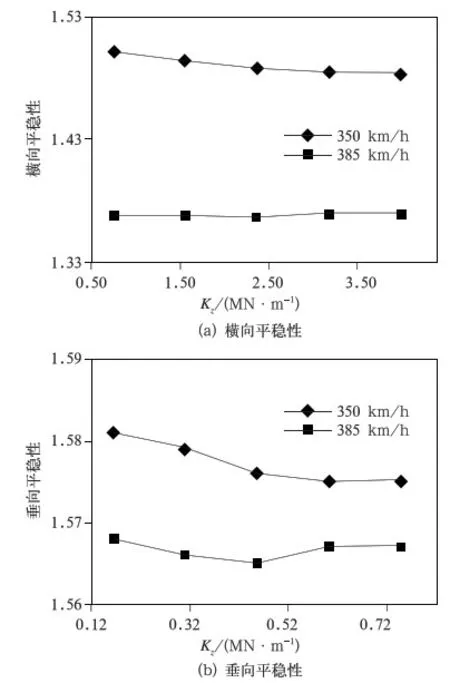
图11 两个速度级下测点3的平稳性随垂向刚度Kz变化的对比(横向刚度Ky=0.16 MN/m)

由图11和图12可知，动车在速度350 km/h下的车体平稳性均略大于在速度385 km/h下的车体平稳性。文献[7]对京津城际铁路高速列车在350 km/h及以上的行驶速度下的车辆振动状态进行了试验分析，有如下规律：在一定范围内，速度提升，车体的横向、垂向振动加速度均有不同程度的减小。由式(1)可知，车体平稳性由振动加速度计算而来。因此，本文针对350 km/h和385 km/h两个速度级而言，速度增大，车体平稳性略有减小，与文献[7]符合。

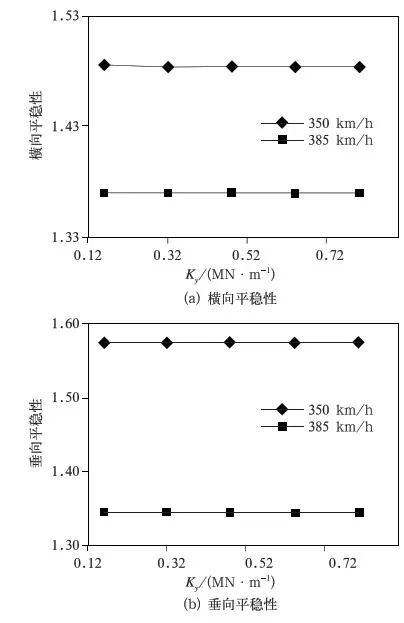
图12 两个速度级下测点3的平稳性随横向刚度Ky变化的对比(垂向刚度Kz=2.91 MN/m)

牵引变压器的振动烈度同样会受到动车运行速度的影响，如图13和图14。

图13 振动烈度随垂向刚度Kz变化图(横向吊挂刚度Ky=0.48 MN/m)

由图13和图14可知，当动车在385 km/h速度级时，其振动烈度较在350 km/h速度级时略有增加。由牵引变压器的主要工作原理和振动机理可知[8]，随着列车运行速度的提高，外界激励对牵引变压器的影响加剧，增加了牵引变压器的振动，不过还需要通过充分的理论分析和大量试验进行验证。

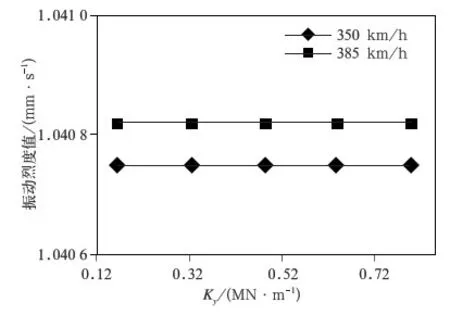
图14 振动烈度随横向刚度Ky变化图(垂向吊挂刚度Kz=2.18 MN/m)

4 结 论

针对原始实测信号的具体特点，增加仿真计算的实用性，分别采用快速傅里叶变换和矩阵变换得到位移激励信号，加载至仿真模型，通过对计算结果的分析，得出如下结论：

(1) 牵引变压器垂向吊挂刚度对车体的横向、垂向平稳性影响较大。其中当动车运行速度为350 km/h时，在垂向吊挂刚度Kz=3.64 MN/m时车体平稳性最小；当动车运行速度为385 km/h时，在垂向吊挂刚度Kz=2.18 MN/m时车体平稳性最小。

(2) 牵引变压器的横向吊挂刚度对车体的平稳性几乎没有影响。

(3) 牵引变压器吊挂刚度的改变对其振动烈度影响不大。

(4) 385 km/h的运行速度下车体平稳性指标值比350 km/h的略小。

(5) 385 km/h的运行速度下牵引变压器的振动烈度比350 km/h的略有增大。

[1] 任晋峰.高铁车辆车体振动基础性研究[D].大连:大连交通大学，2012.

[2] 余建勇,张立民,黄晓宇,唐琴.车下吊挂设备对整备车车体模态的影响[J].噪声与振动控制，2012,05:97-99.

[3] 蓝剑红.CRH3型动车组车体刚度有限元分析[D].成都:西南交通大学，2012.

[4] GB 5599-85.铁道车辆动力学性能评定和试验鉴定规范[S].北京:国家标准局,1985.

[5] GB 5913-86.柴油机车车内设备机械振动烈度的评定方法[S].北京:国家标准局,1986.

[6] 班希翼.更高速列车牵引变压器连接参数优化设计[D].成都:西南交通大学，2014.

[7] 张曙光.高速列车设计方法研究[M].北京:中国铁道出版社，2009.

[8] 黄晓宇.高速列车车体与牵引变压器耦合振动研究[D].成都:西南交通大学，2013.

Hanging Stiffness’ Effect on MU Vehicle and Traction Transformer Vibration Evaluation Indexes

QUJingjing，ZHANGLimin

(The State Key Laboratory of Traction Power,Southwest Jiaotong University, Chengdu 610031 Sichuan,China)

A vehicle-transformer finite element model is constructed to research the vibration evaluation indexes of the vehicle and the traction transformer. The model is stimulated by signal from two different velocities when the hanging stiffness between vehicle and traction transformer are changing. The vibration response of vehicle and transformer is obtained to calculate the ride index and vibration intensity. The curves are drawn out to summarize the changing trends of the vibration evaluation indexes: At the speed of 350 km/h the ride indexes decrease with the increasing vertical hanging stiffness; At the speed of 385km/h the ride indexes decrease then increase with the increasing vertical hanging stiffness; The ride indexes have no change with the increasing horizontal hanging stiffness; The vibration intensity of the traction transformer is unchanging as the hanging stiffness increase. Finally, the conclusions of the study are summarized. Hanging stiffness have little effect on traction transformer; the vertical hanging stiffness have greater influence on the ride index than the horizontal ones.

vibration and wave; vehicle-transformer; hanging stiffness; ride index; vibration intensity

1008-7842 (2015) 06-0035-06

)女，硕士生(

2015-05-19)

U264.3

A

10.3969/j.issn.1008-7842.2015.06.09