高速列车空心轴的边缘效应及微动分析*

张 雨， 张开林， 王晓鹏， 王秋实

(西南交通大学 牵引动力国家重点实验室， 四川成都 610031)

高速列车空心轴的边缘效应及微动分析*

张 雨， 张开林， 王晓鹏， 王秋实

(西南交通大学 牵引动力国家重点实验室， 四川成都 610031)

利用有限元ANSYS软件仿真与弹性力学理论对比分析某高速列车轴箱轴承与空心轴过盈配合产生的边缘效应，研究了车轴空心系数对边缘效应应力集中程度的影响规律，同时结合微动磨损理论分析增大车轴孔径在配合边缘区产生裂纹的工程现象，研究表明，空心车轴的空心系数不宜超过0.5，研究结果为空心车轴的设计、运用提供理论参考。

空心轴; 边缘效应; 有限元; 微动磨损

铁路车辆采用轴箱装置将轮对与转向架联系起来，使轮对的高速旋转运动转化为车体沿线路的平动，作为铁路车辆现代化的技术之一的轴箱滚动轴承的使用，大大降低了车辆起动阻力和运行阻力，保证了高速列车的安全运行[1]。轴箱滚动轴承与车轴采用过盈配合，合适的过盈量可以有效防止轴承与车轴之间发生滑动，避免车轴与轴承之间的磨损和温升，能够充分发挥轴承的承载能力，延长使用寿命。现代铁路车辆为了达到列车轻量化的要求，车轴一般都采用空心轴，合适的轴孔不仅能节约材料，还能够降低簧下质量，提高列车的动力学性能[2]。但在实际运用中，空心车轴经过疲劳评定满足疲劳要求的情况下，仅增大车轴的轴孔径，会导致轴承内圈与车轴的配合边缘区出现裂纹，严重影响车轴的安全使用。过盈配合面的边缘区出现较大的应力集中现象，称之为边缘集中效应，是导致轴承与车轴之间发生微动磨损的重要因素。利用ANSYS仿真，验证了边缘应力集中现象的存在，结合弹性力学理论分析车轴孔径对边缘效应的影响，并运用微动磨损理论解释增大孔径在配合边缘区产生裂纹的机理。

1 过盈配合弹性力学分析

根据弹性力学理论[3]，轴承与车轴的过盈配合，可以把轴承内圈与车轴简化为平面应力状态下的薄壁圆环和厚壁圆筒进行分析。

1.1 轴承内圈内径变化

由于轴承内圈是轴对称结构，切向位移与剪切应力都为零，应力、应变表达式只与径向尺寸有关，各应变分量如下：

(1)

式中εr、εθ为径向、周向应变分量；u为径向位移；r为任意点的径向尺寸。

根据广义胡克定律可以得到平面应力下应力应变关系：

(2)

式中σr、σθ为径向、周向应力；E为材料的弹性模量；μ为材料的泊松比。

极坐标下平衡微分方程：

(3)

结合式(1)～式(3)，得到轴承内圈平面微分方程，如下：

(4)

结合边界条件，当r=b时，径向压力σr=-p，当r=c时，径向压力σr=0，其中b表示轴承内圈的内半径，c表示轴承内圈的外半径，p表示轴承内圈与车轴过盈配合的正压力。由此可以得到，轴承内圈的接触面径向位移u1为：

(5)

式中E1为轴承内圈材料的弹性模量；μ1为轴承内圈材料的泊松比。

1.2 车轴外径变化

对于车轴，根据广义胡克定律可以得到平面应变下应力应变关系：

(6)

结合式(1)、式(3)、式(6)，得到车轴的平面微分方程，如下：

(7)

由边界条件：当r=b时，径向压力σr=-p，当r=a时，径向压力σr=0，其中b表示车轴的外半径，a表示车轴的内半径，p表示轴承内圈与车轴过盈配合的正压力。由此可以得到，车轴的接触面径向位移u2为：

(8)

式中E2为车轴材料的弹性模量；μ2车轴材料的泊松比。

1.3 过盈接触正压力

根据轴承内圈和车轴的过盈配合接触面的径向位移公式，可以得出轴承的过盈配合的过盈量为：

车轴与轴承内圈的配合正压力为：

当车轴与轴承内圈的材料一致时，配合正压力简化为：

(9)

2 过盈配合边缘效应有限元分析

2.1 轴承内圈与车轴建模

以某高速列车的轴箱轴承与车轴为研究对象，建立轴承与车轴过盈配合有限元模型。轴承与车轴的过盈配合模型，可以简化为建立轴承内圈与车轴的配合模型，同时由于轴承与车轴是轴对称结构，建模时只取其结构的四分之一作为计算模型，对称面施加对称约束。轴承内圈外径180 mm，车轴与轴承配合直径140 mm，过盈量取0.30 mm，摩擦系数取0.2，轴承内圈与车轴的材料弹性模量取2.1e5 N/mm2，泊松比为0.3。为精确模拟过盈配合的边缘效应，对接触面及附近的部分网格进行合理细化。车轴与轴承的结构示意图见图1。

图1 车轴与轴承的结构示意图

2.2 边缘效应有限元分析结果

图2 不同空心系数下的Von_Mises等效应力图

图3 不同空心系数下的接触应力图

图4 不同空心系数下的边缘效应因子图

图2、图3表明，不论是接触应力还是等效应力，对于空心系数不同的车轴，其分布规律都大致相同，接触面中段应力分布均匀，边缘效应很明显。随着空心系数的增大，等效应力呈先缓慢后快速下降的趋势，最大等效应力下降幅值相对接触面中间区域等效应力下降幅值较小。当空心系数小于0.5时，最大接触应力基本不变，当空心系数大于0.5时，最大接触应力快速上升。图4表明，随着空心系数的增大，边缘应力集中因子呈指数形式增大，当空心系数大于0.5时，边缘应力集中因子急剧增大，导致边缘区域出现裂纹。

3 过盈配合微动磨损分析

微动是两接触表面的极小振幅(微米级)的运动，通常发生在一个振动环境下的近似紧固配合的接触表面。微动可以造成接触面摩擦磨损，引起构件咬合和松动，加速裂纹的产生和扩展，降低构件的疲劳寿命[4]。轴承与车轴在高速旋转运行时，轴承与车轴的过盈配合，在保持过盈量不变的情况下，过盈区域相对应的节点位移幅值对微动磨损有很大影响[5]。本文在车轮安装座处施加轴重180 kN，约束车轴两端，得到车轴与轴承在轨道上静止时的变形。图5给出不同空心系数下轴承的轴向位移幅值曲线。图6给出不同空心系数下车轴的轴向位移幅值曲线。

图5 不同空心系数下轴承内圈的轴向位移幅值曲线

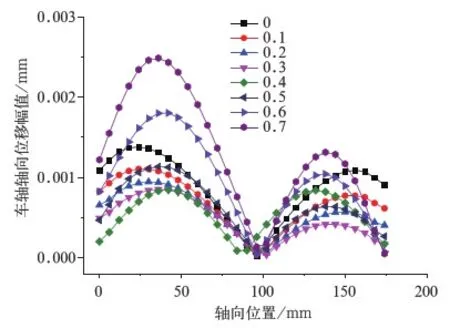
图6 不同空心系数下车轴的轴向位移幅值曲线

由图5可知，不同空心系数下，轴承内圈轴向位移变化幅值的趋势是一致的，都是由中间位置向两边增大，边缘节点轴向位移幅值最大。随着空心系数的增加，轴承轴向位移幅值降低。图6可知，不同空心系数下，车轴的轴向位移幅值都呈现波浪式变化的趋势。随着空心系数的降低，车轴轴向位移幅值下降，当空心系数超过0.5时，车轴轴向位移呈增大趋势。

微动磨损不仅取决于车轴与轴承的变形，更取决于接触区域的相对变形。取车轴与轴承的过盈配合边缘节点的轴向位移幅值，用轴承的轴向应力幅值减去车轴的轴向应力幅值，得到对应节点的轴向相对变形幅值，变化曲线见图7。

图7 不同空心系数下轴承与车轴边缘对应节点的轴向变形幅值曲线

由图7可知，随着空心系数增大，车轴与轴承过盈配合边缘区域应力集中最大值对应节点的相对变形幅值呈非线性下降趋势，当空心系数超过0.5时，位移幅值下降幅度明显增大。

国外研究分析表明[6]，当接触区域位移幅度较大时，接触区易发生滑移现象，这会导致表面产生磨损，不仅可以消除可能存在的初始微裂纹，还可以避免裂纹核的形成。当车轴空心系数超过0.5时，轴承与车轴相对位移幅值大幅降低，造成过盈配合边缘区域初始微裂纹的形成，严重影响车轴的使用寿命。

4 结 论

本文利用有限元对车轴与轴承过盈配合进行仿真，结合弹性力学和微动磨损理论，分析车轴空心系数对边缘效应的影响，探索接触边缘区形成裂纹的机理。通过对比研究，得出以下结论：

(1) 车轴与轴承过盈配合存在严重的边缘效应，随着空心系数的增加，等效应力与接触应力都呈下降趋势；

(2) 随着空心系数的增加，边缘效应因子呈指数形式上升；

(3) 随着空心系数的增加，接触边缘对应节点的轴向相对位移幅值呈非线性下降趋势；

(4) 结合边缘效应和微动磨损，建议车轴空心系数不宜超过0.5，这样既保证了列车的轻量化和良好的动力学性能，又可以减少裂纹的萌生，提高车轴的安全使用寿命。

[1] 严隽耄，傅茂海. 车辆工程[M]. 北京：中国铁道出版社，2008.

[2] 鲍维千. 机车总体及转向架[M]. 北京：中国铁道出版社，2012.

[3] 杨桂通. 弹性力学[M]. 北京：高等教育出版社，1998.

[4] 周仲荣，Vincent L. 微动磨损[M]. 北京：科学出版社，2002.

[5] 贾国海，龚金科，鄂加强等. 齿轮轴过盈配合对轴肩微动磨损的影响研究[J].湖南大学学报(自然科学版)，2013，40(5):31-36.

[6] B.Yang，S.Mall. Mechanics of two-stage crack growth in fretting fatigue[J]. Eng Fracture Mech，2008，75(6):1507-1515.

Fretting Analysis and Edge Effect of High-speed Train Hollow Shaft

ZHANGYu,ZHANGKailin,WANGXiaopeng,WANGQiushi

(Traction Power State Key Laboratory, Southwest Jiaotong University, Chengdu 6130031 Sichuan, China)

This paper analyzed edge effect which caused by the interference fit between axle box bearing and hollow shaft on a high-speed train, by comparing the finite element software ANSYS simulation and the elasticity theory. The impact of hollow shaft coefficient to stress concentration degree on the edge is studied, and is engineering phenomenon of crack initiation in the edge area caused by increasing the hollow shaft inside ratio is analyzed by combining the fretting wear theory. The results show that the hollow coefficient of hollow shaft should not be more than 0.5. It provid theory reference for the design and use of hollow shaft.

hollow axle; edge effect; FEA; fretting wear

1008-7842 (2015) 06-0015-04

*国家自然基金资助项目(51205324);牵引动力国家重点实验室自主研究课题资助项目(2015TPL-T10)

男，硕士研究生(

2015-07-11)

U260.11+1

A

10.3969/j.issn.1008-7842.2015.06.04