ADS的液态LBE-氦气换热器优化

孟瑞雪，蔡 军，淮秀兰,*，陈 飞,2

(1.中国科学院 工程热物理研究所，北京 100190；2.华北水利水电大学，河南 郑州 450011)



ADS的液态LBE-氦气换热器优化

孟瑞雪1，蔡 军1，淮秀兰1,*，陈 飞1,2

(1.中国科学院 工程热物理研究所，北京 100190；2.华北水利水电大学，河南 郑州 450011)

基于遗传算法，分别以火积耗散数和总成本为目标函数，对ADS的液态LBE-氦气换热器进行多参数优化。结果表明，两种优化方法使换热器有效度分别提高10.5%和3.8%，总成本分别降低5.9%和27.0%，但优化过程分别以增加传热面积和牺牲传热性能为代价。综合对比两种优化方法得到的换热器性能、成本消耗、收益等因素，发现以火积耗散数为目标函数的优化方法更具优势。

ADS；遗传算法；换热器优化；火积耗散数；总成本

为实现核电的可持续发展，早在20世纪90年代，核物理学家提出了分离-嬗变的核燃料循环与乏燃料后处理策略。随后，欧盟各国、美、日、俄等核能科技发达国家均制定了与之相应的ADS中长期发展路线。2011年，中国科学院启动ADS战略性先导科技专项[1]，初步采用液态LBE作为一回路冷却剂，而氦气凭借良好的传热特性和化学反应惰性成为二回路冷却介质的选择之一。为深入开展LBE与氦气之间的流动传热特性研究，中国科学院工程热物理研究所设计了LBE-氦气换热综合实验测试平台(LELA)，该实验平台包括LBE回路和氦气回路。

换热器性能优化对提高能源利用率有重要意义，而合理选择目标函数是优化的关键。从经济性角度考虑，总成本最小法是最传统的优化方法，但该方法忽略了传热效果这一因素，在追求低成本的过程中是否降低了换热器性能有待研究；从不可逆损失角度考虑，Bejan[2]最早提出了熵产最小的优化方法，但该方法在逆流换热器传热有效度ε<0.5的情况下出现了“熵产悖论”[3]。Guo等[4]认为熵是表征热功转换过程的物理量，而换热器设计中人们更关心热量传递的速率或效率。通过热电比拟，Guo等[5]引入火积描述物体的传热能力，并基于变分分析，提出了适用于导热过程优化的火积耗散极值原理。通过电热模拟实验研究，过增元等进一步验证了该理论[6]，并通过与熵产最小方法的对比，证明了对于以热量传递为目的的换热器，基于火积耗散极值原理的优化方法更具优势[7]。基于该理论，郭江峰等[8-11]开展了大量换热器优化方面的研究。然而，以往的换热器传热优化大多基于常规流体换热器(水-水换热器等)，关于流动工质为低普朗特数液态金属的换热器优化鲜有报道。

本文分别基于火积耗散极值原理和成本最小方法对新型LBE-氦气换热器进行多参数优化，对比分析两种优化方法获得的结果，验证基于火积耗散极值原理的优化方法在LBE-氦气换热器优化中的可行性和相对优势。

1 换热器物理模型

LELA采用管壳式换热器作为两个回路间的换热设备，流动形式为单管程-单壳程逆流流动，换热管呈正三角形排列，管程流体为LBE，壳程流体为氦气。换热器的三维简化模型及管孔布置如图1所示，其已知边界条件和初步设计的结构参数列于表1。

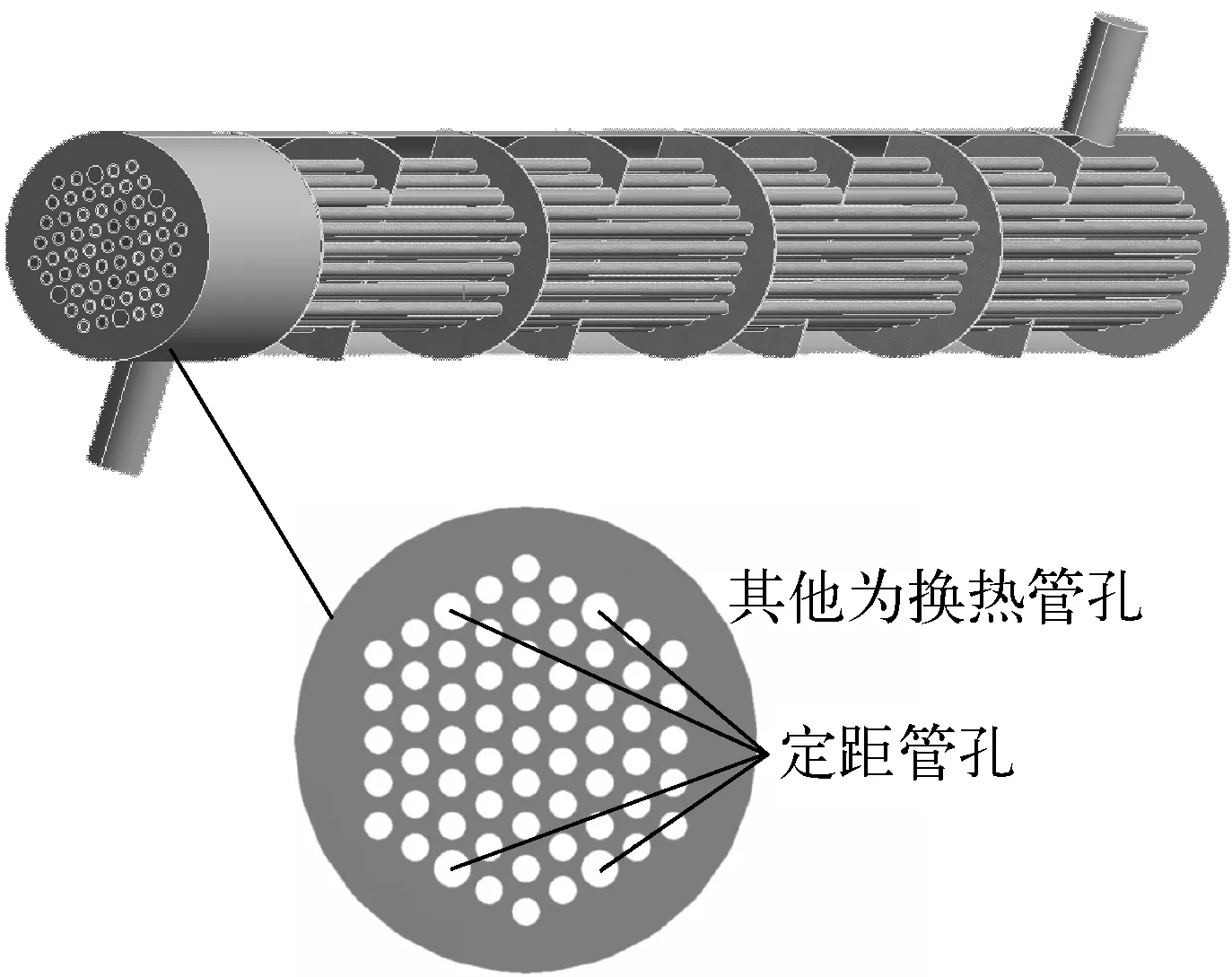
图1 LELA换热器简化模型Fig.1 Simplified heat exchanger model of LELA

表1 换热器参数Table 1 Parameters of heat exchanger

2 优化的理论依据

2.1 对流传热系数

与常规换热器不同的是，该换热器采用液态金属LBE作为管程工质，其普朗特数Pr(10-2量级)远小于常规流体的普朗特数(>0.6)，适用于常规流体的传热关联式不再适用于LBE。基于此，Chen等[12]证明了在恒热流条件下，Cheng等[13]提出的传热关联式(式(1))能更准确描述LBE的传热特性。

Nut=A+0.018Pe0.8

(1)

(1)

管程LBE的对流传热系数可写为：

(2)

其中：λ为流体导热系数；下标t代表管侧；Nu、Pe分别为努塞尔数和贝克莱数。

壳程对流传热系数采用通用的Bell-Delaware方法计算，换热器总传热系数K、传热有效度ε、压降Δp以及换热器运行总消耗功率Wp依据文献[14]计算得出。

2.2 火积耗散数

Guo等[4]定义火积Eh为定容热容量QVh与温度乘积的一半，反映了流体的热传递能力。

(3)

其中，QVh=McVT，则有：

(4)

火积耗散数反映了流体热传递能力损失，由有限温差传热及流体阻力等因素引起，等于流体入口处的火积与出口处的火积之差。有限温差传热引起的换热器的火积耗散数ΔET为：

(5)

将液态LBE和氦气近似视为定物性流体，则(cV)h1=(cV)h2，(cV)c1=(cV)c2，得：

(6)

将液态LBE视为不可压缩液体，氦气视为理想气体，流体阻力引起的换热器的火积耗散数ΔEp[15]为：

(7)

换热器的总火积耗散数为：

(8)

将其无量纲化，得换热器的火积耗散数[16]：

(9)

其中：下标1、2、c、h分别代表进口、出口、冷流体、热流体；cV为比定容热容，J/(kg·K)；T为温度，K；ρ为密度，kg/m3；p为压力，MPa；Rs为壳侧氦气的压缩因子；Q为实际换热量，W，根据Q=εQmax计算得出，Qmax为换热器最大可能换热量[14]。

2.3 总成本消耗

本文研究的管壳式换热器采用不锈钢材料，运用经验公式计算成本及收益[17]。

投入成本Ci有：

(10)

运行成本Cod有：

(11)

总成本Ctot有：

(12)

由于传热有效度提高而增加的收益为：

ΔC=CE(Mcp)min(Th1-Tc1)ΔεHyr

(13)

其中：a1=8 000；a2=259.2；a3=0.91；S为换热器总表面积，m2；yr为运行年数；CE为能量成本，CE=1.2 ￥/(kW·h)；H为每年的运行时长，取7 000 h；i为年折旧率，取10%；cp为比定压热容，J/(kg·K)。

3 优化设计与结果分析

3.1 遗传算法

遗传算法以自然选择和遗传理论为基础，是一种将生物进化适者生存规则与群体内部染色体随机信息交换、变异机制相结合的全局寻优算法[18]，该算法能得到一组近似最优解。本文基于遗传算法，分别以火积耗散数和总成本为目标函数进行优化，其流程如图2所示。

3.2 优化设计

选定优化参数[do，n，Bs，Al，Tc2]，其中，换热管外径do取标准值[19]；Bs为折流板间距与壳体内径之比，取标准值[20]。优化参数取值范围下限为[0.010，20，0.2，1.854 6，663]，上限为[0.057，500，1，2.941 3，763]。

根据图2所示算法，编写相应的适应度函数和相关计算程序。设定变量个数为5，初始种群数为50，交叉概率为0.5，变异概率为0.1，遗传代数为500。目标函数的收敛曲线如图3、4所示，可看出，随遗传代数的增加，火积耗散数ΔEN和总成本Ctot均迅速减小，并在100代后趋于稳定，最终达到最小值。

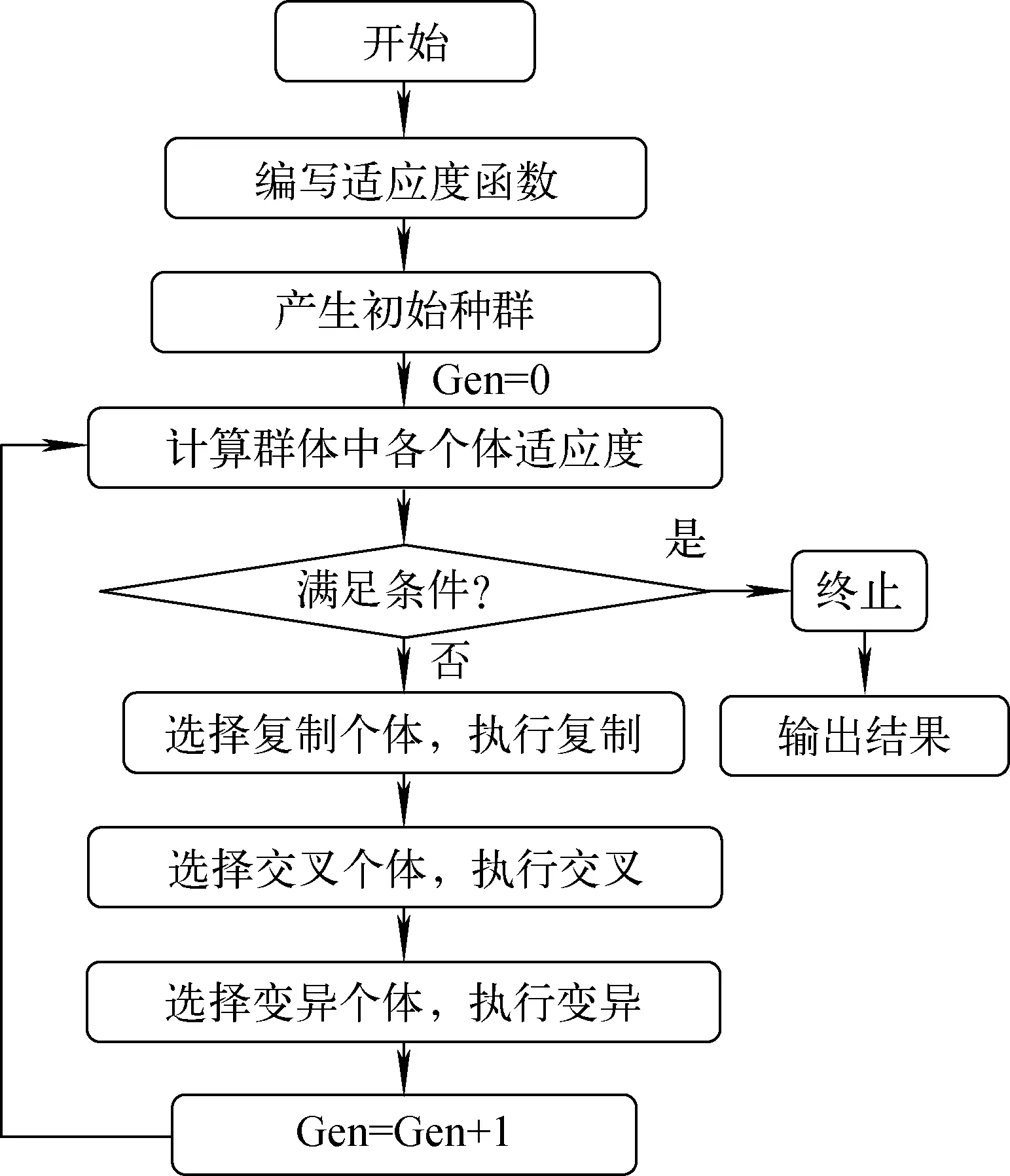
图2 遗传算法流程图Fig.2 Flow chart of genetic algorithm

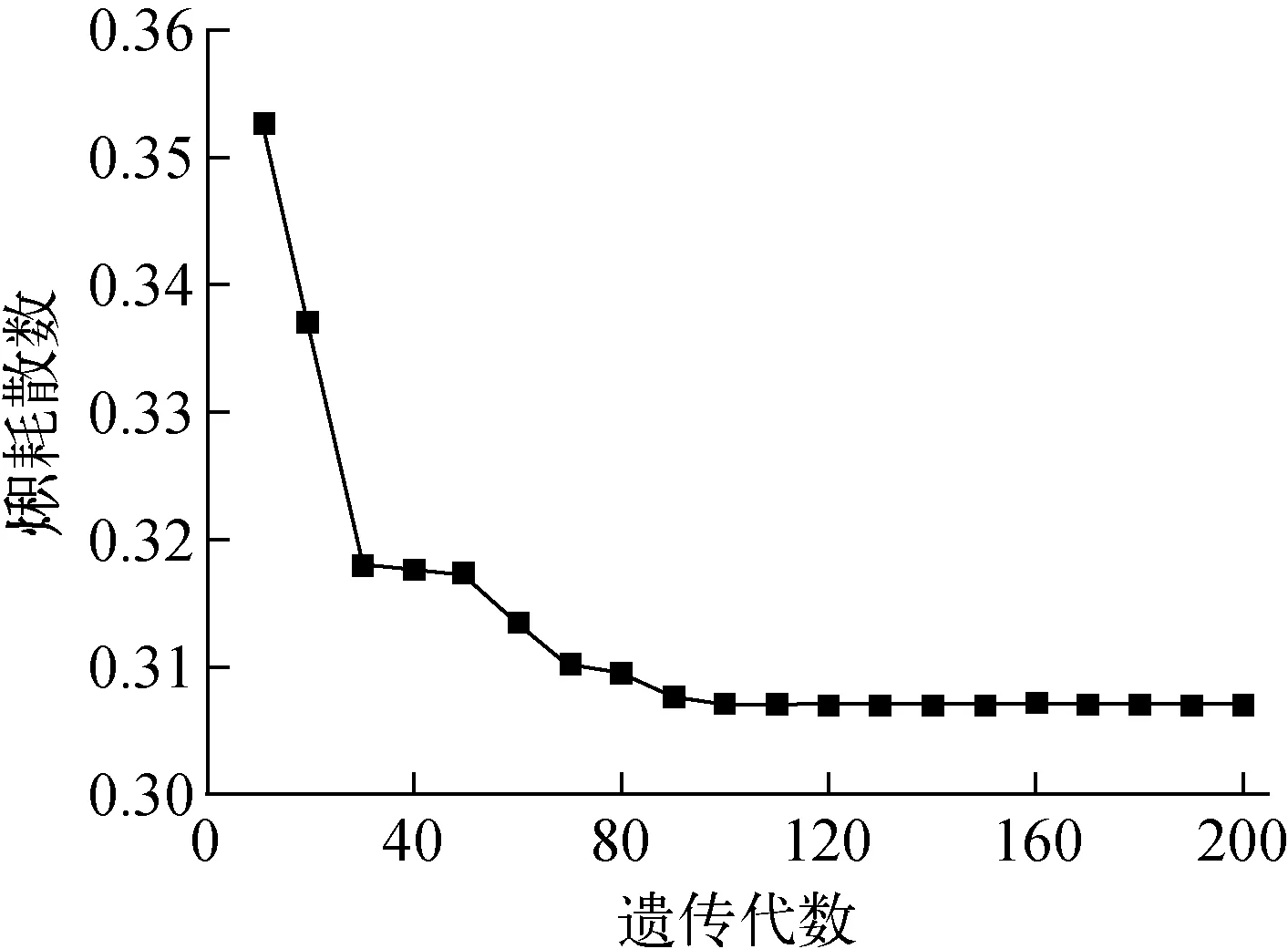
图3 火积耗散数逐代收敛曲线Fig.3 Convergence curve of entransy dissipation number with generation

3.3 结果分析

1) 以火积耗散数为目标函数的优化结果

传热单元数NTU反映了换热器传热能力的大小，ε为实际传热量与最大可能传热量的比值[14]，其随火积耗散数的变化曲线如图5所示。可看出，随火积耗散数的减小，传热单元数及传热有效度均不断增大，尤其火积耗散数小于0.33后，两参数均随火积耗散数的减小迅速增大。这表明，随着火积耗散数的减小，换热器的传热能力与实际传热量均得到提升，换热器性能大幅提高。

图4 总成本逐代收敛曲线Fig.4 Convergence curve of total cost with generation

图5 传热有效度、传热单元数随火积耗散数的变化曲线Fig.5 Variation of effectiveness and heat transfer unit number with entransy dissipation number

图6 总消耗功率、传热面积随火积耗散数的变化曲线Fig.6 Variation of total consumption power and heat transfer area with entransy dissipation number

换热器传热面积Fo及总消耗功率Wp随火积耗散数的变化曲线如图6所示。可看出，随火积耗散数的减小，换热器消耗的总功率随之减小，但所需的传热面积却随之大幅增加，使得换热器的运行成本有所减小，而投入成本有所增加。

2) 以总成本为目标函数的优化结果

传热单元数及传热有效度随总成本的变化曲线如图7所示。可看出，随总成本的降低，传热单元数及传热有效度呈下降趋势，尤其在总成本小于2.5万元后，两参数随总成本的减小迅速下降。这表明，随着总成本的减小，换热器的传热能力及传热量均不断降低，换热器性能大幅下降。

图7 传热有效度、传热单元数随总成本的变化曲线Fig.7 Variation of effectiveness and heat transfer unit number with total cost

换热器传热面积及其总消耗功率随总成本的变化曲线如图8所示。可看出，随总成本的减小，换热器所需传热面积及总消耗功率均近似呈直线下降趋势，从而使换热器的投入成本和运行成本均大幅减小，这也与目标函数的优化趋势一致。

图8 总消耗功率、传热面积随总成本的变化曲线Fig.8 Variation of total consumption power and heat transfer area with total cost

3) 优化结果对比分析

优化结果与初始参数对比列于表2。

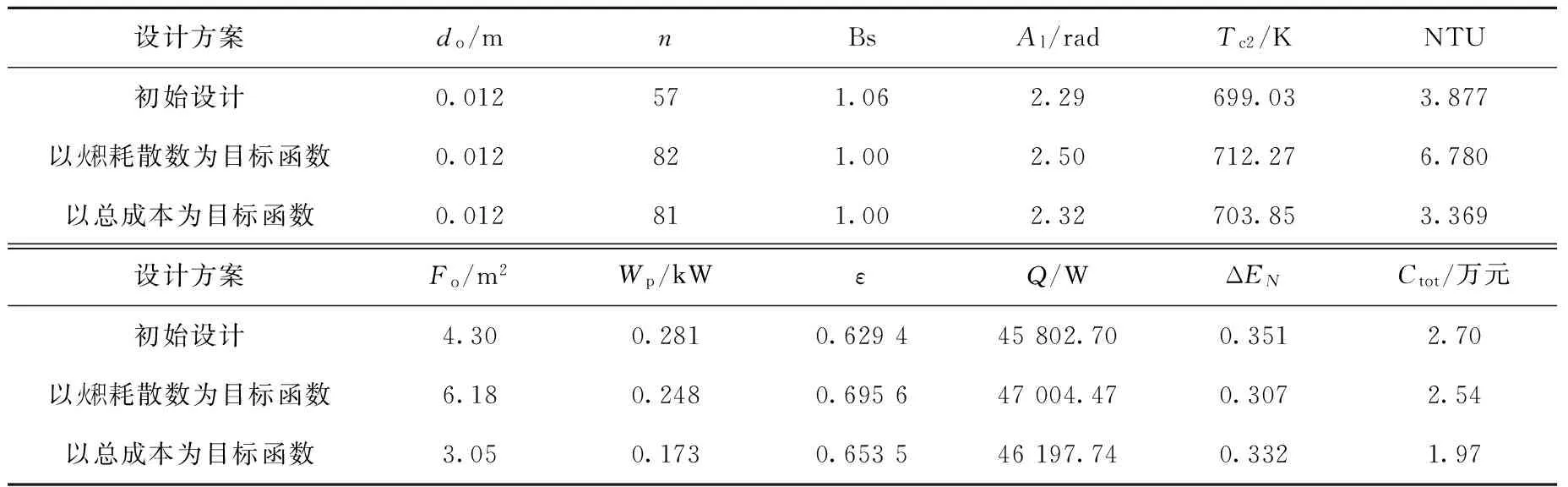
表2 优化结果对比Table 2 Comparison of optimization results

对比Q发现，两种优化方法得到的换热器总传热量均有所增加；对比ε得出，以火积耗散数为目标的优化方法使换热器的传热有效度较优化前提高10.5%，以总成本为目标的优化方法提高3.8%。由此表明，两种优化方法均提高了换热器的传热性能和传热量，以火积耗散数为目标的优化得到的换热器性能更好。

对比Ctot发现，以火积耗散数为目标的优化方法使换热器的总成本较优化前降低5.9%，以总成本为目标的优化方法降低27.0%。由此表明，两种优化方法均使换热器的总成本有所降低，但以火积耗散数为目标的优化得到的换热器比以总成本为目标的优化得到的换热器多消耗总成本0.57万元。

计算得出，以火积耗散数为目标的优化比以总成本为目标的优化得到的换热器传热有效度大，Δε=0.042 1。由式(13)计算得，增加的有效度使换热器每年增加收益ΔC=2.389 7万元，足以抵消总成本的增加。从换热器成本及收益角度综合考虑，以火积耗散数为目标的优化仍具有优势。

观察表中5个优化参数do、n、Bs、Al、Tc2可看出，两种优化方法得到的结果主要由n的大幅增加、Al的增大及Tc2的升高得到。换热管直径始终不变，说明对于该换热器，管径12 mm已是最优值。

4 结论

本文运用遗传算法，分别以火积耗散数和总成本为目标，对ADS的液态LBE-氦气换热器进行了优化研究，得到如下结论。

1) 以火积耗散数为目标优化时，随火积耗散数的减小，换热器性能大幅提高，总消耗功率的降低使运行成本相应减小，但传热面积的增大使投入成本增加。

2) 以总成本为目标优化时，随总成本的降低，传热单元数及有效度大幅下降。说明该优化方案虽使换热面积和总消耗功率减小，降低了制造和运行成本，但也很难得到最优的换热效果。

3) 相对于初始设计，两种优化方法均提高了换热器性能，并降低了总成本。就传热性能而言，以火积耗散数为目标的优化方法具有绝对优势；就成本而言，以火积耗散数为目标优化得到的换热器成本虽然高于以总成本为目标优化得到的换热器成本，但不足以抵消其传热有效度增加带来的收益。因此，以火积耗散数最小为目标的优化方法更能实现最优的换热效果。

4) 基于火积耗散极值原理的优化方法在LBE-氦气换热器的优化中是可行的，且在其他液态金属换热器的优化中具有普适性。

[1] 詹文龙，徐瑚珊. 未来先进核裂变能ADS嬗变系统[J]. 中国科学院院刊，2012，27(3)：375-381.

ZHAN Wenlong, XU Hushan. Advanced fission energy program: ADS transmulation system[J]. Journal of Chinese Academy of Sciences, 2012, 27(3): 375-381(in Chinese).

[2] BEJAN A. Second law analysis in heat transfer[J]. Energy and Buildings, 1980, 5(8-9): 720-732.

[3] BEJAN A. Advanced engineering thermodynamics[M]. New York: Wiley, 1997.

[4] GUO Zengyuan, CHENG Xinguang, XIA Zai-zhong. Least dissipation principle of heat transport potential and its application in heat conduction optimization[J]. Chinese Science Bulletin, 2003, 48: 406-410.

[5] GUO Zengyuan, ZHU Hongye, LIANG Xin-gang. Entransy: A physical quantity describing heat transfer ability[J]. Heat Mass Transfer, 2007, 50: 2 545-2 556.

[6] 朱华晔，陈泽敬，过增元. 火积耗散极值原理的电热模拟实验研究[J]. 自然科学进展，2007，17(10)：1 692-1 698.

ZHU Huaye, CHEN Zejing, GUO Zengyuan. Investigation of the principle of extremum entransy dissipation in electrothermal simulation[J]. Progress in Nature Science, 2007, 17(10): 1 692-1 698(in Chinese).

[7] 柳雄斌，孟继安，过增元. 换热器参数优化中的熵产极值和火积耗散极值[J]. 科学通报，2008，53(24)：3 026-3 029.

LIU Xiongbin, MENG Ji’an, GUO Zengyuan. Extreme entropy generation and extreme entransy dissipation in heat exchanger optimisation[J]. Chinese Science Bulletin, 2008, 53(24): 3 026-3 029(in Chinese).

[8] 郭江峰. 换热器的热力学分析与优化设计[D]. 济南：山东大学，2011.

[9] GUO Jiangfeng, XU Mingtian, CHENG Lin. The entransy dissipation minimization principle under given heat duty and heat transfer area conditions[J]. Chinese Science Bulletin, 2011, 56(20): 2 071-2 076.

[10]LI Xuefang, GUO Jiangfeng, XU Mingtian, et al. Entransy dissipation minimization for optimization of heat exchanger design[J]. Chinese Science Bulletin, 2011, 56(20): 2 174-2 178.

[11]郭江峰，许明田，程林. 基于火积耗散数最小的板翅式换热器优化设计[J]. 工程热物理学报，2011，32(5)：827-831.

GUO Jiangfeng, XU Mingtian, CHENG Lin. Optimization design of plate-fin heat exchanger based on entransy dissipation number minimization[J]. Journal of Engineering Thermaphysics, 2011, 32(5): 827-831(in Chinese).

[12]CHEN Fei, HUAI Xiulan, CAI Jun, et al. Investigation on the applicability of turbulent-Prandtl-number models or liquid lead-bismuth eutectic[J]. Nuclear Engineering and Design, 2013, 257: 128-133.

[13]CHENG X, TAK N I. Investigation on turbulent heat transfer to lead-bismuth eutectic flows in circular tubes for nuclear applications[J]. Nuclear Engineering and Design, 2006, 236: 385-393.

[14]史美中，王中铮. 热交换器原理与设计[M]. 南京：东南大学出版社，2009.

[15]许明田，程林，郭江峰. 火积耗散理论在换热器设计中的应用[J]. 工程热物理学报，2009，30(12)：2 090-2 092.

XU Mingtian, CHENG Lin, GUO Jiangfeng. An application of entransy dissipation theory to heat exchanger design[J]. Journal of Engineering Thermaphysics, 2009, 30(12): 2 090-2 092(in Chinese).

[16]GUO Jiangfeng, CHENG Lin, XU Mingtian. Entransy dissipation number and its application to heat exchanger performance evaluation[J]. Chinese Science Bulletin, 2009, 54(15): 2 708-2 713.

[17]CAPUTO A C, PELEGEGGE P M, SALINI P. Heat exchanger design based on economic opitimization[J]. Applied Thermal Engineering, 2008, 28: 1 151-1 159.

[18]雷英杰. MATLAB遗传算法工具箱及应用[M]. 西安：西安电子科技大学出版社,2005.

[19]中华人民共和国国家质量监督检疫总局，国家标准化管理委员会. GB 13296—2007 锅炉/热交换器用不锈钢无缝钢管[S]. 北京：中国标准出版社，2007.

[20]国家质量监督检疫总局，国家标准化管理委员会. GB 151—1999 管壳式换热器[S]. 北京：中国标准出版社，1999.

Optimization of Liquid LBE-helium Heat Exchanger in ADS

MENG Rui-xue1, CAI Jun1, HUAI Xiu-lan1,*, CHEN Fei1,2

(1.InstituteofEngineeringThermophysics,ChineseAcademyofSciences,Beijing100190,China;2.NorthChinaUniversityofWaterResourcesandElectricPower,Zhengzhou450011,China)

The multi-parameter optimization of the liquid LBE-helium heat exchanger in ADS was conducted by genetic algorithm with entransy dissipation number and total cost as objective functions. The results show that the effectiveness of heat exchanger increases by 10.5% and 3.8%, and the total cost reduces by 5.9% and 27.0% respectively with two optimization methods. Nevertheless, the optimization processes trade off increasing heat transfer area and decreasing heat transfer effectiveness respectively against achieving optimization targets. By comprehensively considering heat exchanger performance and cost-benefit, the optimization method with entransy dissipation number as the objective function is found to be more advantageous.

ADS; genetic algorithm; heat exchanger optimization; entransy dissipation number; total cost

2014-03-21;

2014-05-28

中国科学院战略性先导科技专项资助项目(XDA03010500)

孟瑞雪(1988—)，女，河北衡水人，硕士研究生，工程热物理专业

*通信作者：淮秀兰，E-mail: hxl@mail.etp.ac.cn

TK172

A

1000-6931(2015)07-1266-07

10.7538/yzk.2015.49.07.1266