基于Cokriging的三维重力张量随机反演
2015-05-03黄天统朱自强鲁光银曹书锦
黄天统, 朱自强, 鲁光银, 曹书锦
(中南大学 地球科学与信息物理学院,长沙 410083)
基于Cokriging的三维重力张量随机反演
黄天统, 朱自强*, 鲁光银, 曹书锦
(中南大学 地球科学与信息物理学院,长沙 410083)
重力张量是重力位的二阶导数,与传统的重力测量相比,重力张量具有更高的分辨率。协同克里格法是地质统计学中常见的一种方法,使用协同克里格法对三维重力张量各分量数据进行随机反演。由于位场数据在深度方向上的分辨率较低,因此需通过使用深度加权函数和钻孔数据来解决这一问题,对比了带深度加权和带钻孔数据的协同克里格反演结果。反演结果表明,协同克里格法能够较好地反演重力张量各分量数据,两种方式都能够较好地反演出地下异常位置,带深度加权的协同克里格法反演出来的密度值与实际值有一定的偏差,而带钻孔数据的协同克里格法能够较好地反演出剩余密度值,并且对于不同埋深的异常体都能很好地反映。
协同克里格; 重力张量; 反演; 钻孔数据; 深度加权函数
0 引言
作为一种前沿性的重力测量方法,重力张量测量在国外开展已有十余年。与常规的重力测量相比,重力张量测量的是重力位的二阶导数,对地下介质密度的变化反映更加灵敏,能够更加直接地突出目标体的边界[1],因此选择一种合理的数值算法对重力梯度张量进行反演具有重要意义。LI Xiong[2]提出的全空间的重力梯度张量计算公式,为重力梯度张量理论计算提供了依据,也是重力梯度张量反演理论的基础;李耀国[3-4]在重磁数据三维反演时,为了提高反演在深度方向的分辨率,引入了深度加权函数;Zhdanov等人[5]实现了三维重力梯度张量数据聚焦正则化反演,反演结果对异常体的尖锐边界反映明显;王浩然[6]将李耀国的方法应用到重力梯度张量反演,构建了联合反演目标函,并对反演密度进行约束,反演结果能够很好地反映地下异常体位置和剩余密度;陈少华[7]利用预条件共轭梯度对重力梯度张量各分量数据进行联合反演取得了很好的效果。
地质统计学是数学地质领域中发展迅速且应用广泛的一门学科,它是在区域化变量理论的基础上,运用变差函数这一主要工具,研究变量在空间分布的随机性与结构性[8-9]。协同克里格法[10]则把区域化变量的最佳估值方法从单一属性发展到两个以上的协同区域化属性。国外有部分学者将地质统计学方法运用到地球物理反演方面,取得了一定的成果。Bosch[11-12]对密度的后验概率方程应用蒙特卡罗方法较好地反演出初始模型;Chasseriau[13]应用先验模型的协方差对重力数据进行了反演。协同克里格法能够简便地结合钻孔数据,使得反演结果更加准确可靠。Shamsipour[14-15]等人利用地质统计学结合钻孔数据对重力数据进行了三维cokring反演和条件模拟,反演结果能够准确地确定异常边界和剩余密度。Erwan Gloaguen等人[16]将协同克里格法运用于钻孔地质雷达波速反演取得了很好的效果。作者将协同克里格方法应用于重力张量的反演,并结合深度加权和钻孔数据,反演结果能够较好地反演出地下异常体的边界和剩余密度值。
1 方法原理
1.1 重力张量模型正演
重力张量是重力位的二阶导数,在笛卡尔坐标系下,根据牛顿万有引力定律,一个剩余密度为ρ,体积为V的地质体,在它外部空间中的任意一点的重力位为:
(1)
其中:G是万有引力常量;r是任意观测点P(x,y,z)到异常点Q(ξ,η,ζ)的方向矢量。那么重力张量表达式写成矩阵形式:
(2)
式中:Γ表示全重力梯度张量。重力张量共有9个分量,由于在无源空间里重力的旋度和散度都为"0",因此重力梯度张量中只有5个独立分量Vxx、Vxy、Vxz、Vyz、Vzz。对于长方体,重力张量各分量的离散正演公式[2]为:
(3)
(4)
(5)
(6)
(7)
(8)
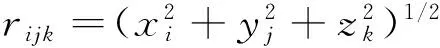
若地下剖分的长方体单元格的数量为m,测点数为n,将重力张量各分量写成统一的表达式:
Vαβ=Sαβρ
(9)
其中:α、β分别取值为x、y、z,不同的取值对应不同的重力张量分量;Vαβ为n×1维的观测数据向量;ρ为m×1维单元格剩余密度的值;Sαβ为n×m维的雅克比矩阵;矩阵S的元素Sij表示第j个单元格在第i个测点的响应。
1.2 协同克里格原理
协同克里格方法是地质统计学中重要而且十分有效的方法之一,它既能反映统计相关信息,又能反映空间位置的相关信息[17]。协同克里格方法是通过运用主要变量和次要变量的空间相关性来提高主变量的估计。在这里剩余密度ρ以及其估计值ρ*是主要变量,重力张量V是次要变量。假设重力张量和剩余密度的期望是为“0”,即E[ρ]=E(V)=0,若期望不为零,可先减去平均值,最后再补偿。可以从 式(10)矩阵的对角元素上求出估计方差:
(10)
其中:CVV是重力张量的协方差矩阵;Cρρ是密度的协方差矩阵;CρV是密度和重力张量的交互协方差矩阵;Λ是权系数矩阵;ρ和V是多维的随机变量。最小化式(10)的估计方差可以得到一个简单的协同克里格的解:
CVVΛ=CVρ
(11)
最后利用一个理想的权系数可以从重力张量场中求解出密度的估计值:
ρ*=ΛTV
(12)
协同克里格方差就可以通过公式(13)求解:
σck=diag(Cρρ-ΛTCVρ)
(13)
矩阵A=Cρρ-ΛTCVρ中的非对角元素表示估计误差的协方差。
1.3 协同克里格反演
从公式(9)可以看出,剩余密度和重力张量的协方差矩阵是线性相关的:
CVV=SCρρST+C0
(14)
其中:C0是重力张量观测误差的协方差矩阵,一般情况下,C0是一个对角阵。
CVρ=SCρρ
(15)
如果不考虑观测误差,即C0=0,就有式(16)成立:
=S(SCρρ)T(SCρρST)-1V=V
(16)
从式(16)可以看出,在没有误差的情况下,利用协同克里格计算出来的剩余密度就等于观测场的剩余密度。
由于重力张量数据和其他位场数据一样,在深度方向上的分辨率较低,反演出来的构造都会集中在地表。因此要想加强深度方向上的分辨率还得进行一定的处理。如果已知钻孔的数据资料,则可以提高深度方向上的分辨率,如果钻孔处的剩余密度值为ρF,通过扩展式(11)可以得到类似的公式:
(17)
CVρF为重力张量与钻孔剩余密度的交互协方差,矩阵CρFV=CVρFT为钻孔剩余密度与重力张量的交互协方差,CρFρ为钻孔剩余密度与区域剩余密度的交互协方差,Λ和Φ是最小化方差估计的权系数,Giroux[18]推导了式(17)中各变量的求取方法。
ρ*=ΛTV+ΦTρF
(18)
那么协同克里格方差就可以通过式(19)求解:
(19)
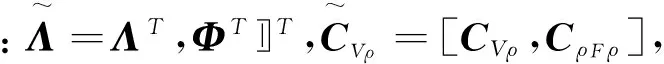
在没有钻孔数据的情况下,则可以通过引入深度加权因子[4]来补偿深度方向上的衰减,从而增强深度方向的分辨率。
(20)
其中:z是网格单元的中心埋深;β一般情况下取一个接近2的数;z0为一个取决于长方体单元尺寸和埋深的常数。通过调节z0和β的值,合理补偿地下构造在深度上的分布。
1.4 模型协方差估计
假设E[ρ]=E(V)=0,那么观测的数据的协方差矩阵可以写成[14]:
(21)
由于测区密度在水平方向被截断,使协方差矩阵CVV、CVρ都是不稳定的,因此传统的估计方法不能直接运用。Asli等人[19]运用理论变差和实际变差图像的方法(V-V图像法)解决了这一问题。
1)假定一个剩余密度协方差矩阵Cρρ的初始模型。变差函数与协方差矩阵之间的关系式为:
C(h)=C(0)-γ(h)
(22)
γ(h)为模型的变差模型,例如式(23)为球体变差模型,h为空间距离,通过改变变差模型可以调节Cρρ。对于简单的模型球体变差模型能够很好地拟合,若当球体变差模型无法满足拟合精度要求时,可以选择其他变差模型[20]。

(23)
其中:C1为块金常数;C1+C为基台值;C为拱高;a为变程。
2)根据式(21)计算CVV的实验值CVV-exp,根据式(14)计算CVV的理论值CVV-th,并将两个矩阵重排成两个向量νexp和νth。


(24)

2 模型算例
分别以单个长方体和水平方向上不同埋深、不同密度的两个长方体为研究模型,利用协同克里格的方法对两个模型进行反演分析。
2.1 模型一
将场源空间划分为20×20×20=8 000个单元格,在x、y、z三个方向单元格的长度均为50 m,如图1(a)所示,场源空间存在一个400 m×400 m×200 m的长方体,长方体顶部埋深为200 m,底部埋深为400 m,长方体水平中心位置为(475 m,475 m),剩余密度为1 000 kg/m3,x、y方向点距为50 m,测线长度为1 000 m,钻孔位置在(475 m,475 m),钻孔数据如图1(b)所示,模型一重力张量正演结果如图2所示。
运用V-V图像法,取步长Nlag=100,调节模型协方差矩阵使理论协方差矩阵和实验协方差相近,以Vzz的反演为例,通过拟合变差模型,最小化式(24),得到球体变差模型C=7 000 (kg/m3)2,C1=0,ax=350 m,ay=350 m,az=350 m。反演结果如图3所示。

图1 模型一图

图2 模型一重力张量正演结果
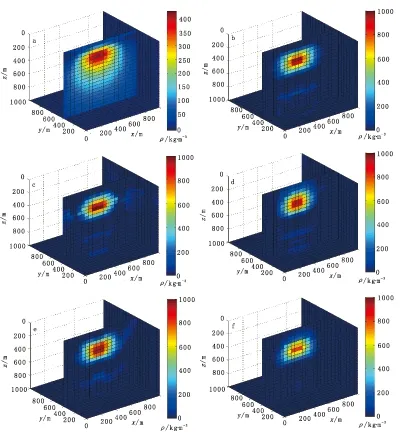
图3 模型一协同克里格反演结果(切片在y=400 m处)
对比图3(a)和图3(b),对于单个的长方体,带深度加权的协同克里格反演和带钻孔数据的协同克里格反演,都能够比较准确地反演出地下异常的位置,但带钻孔数据的协同克里格反演对异常位置确定的效果,明显优于带深度加权的协同克里格反演的结果。对于反演的密度值,带深度加权的协同克里格反演出来的密度值与初始模型有较大的偏差,而带钻孔数据的协同克里格反演能够较好地反演出密度值。观察图3(b)至图3(f)可以看出,结合钻孔数据,重力张量各分量反演出来的结果,都能较好地确定地下异常体的位置和剩余密度值。
2.2 模型二
如图4(a)所示,地下空间水平方向存在两个长方体,大小都为200 m×200 m×200 m,左侧长方体水平中心位置为(275 m,500 m),顶部埋深为200 m,底部埋深400 m,剩余密度为1 000 kg/m3;右侧长方体水平中心位置为(675 m,500 m),顶部埋深为100 m,底部埋深300 m,剩余密度为500 kg/m3,钻孔位置在(300 m,500 m)和(700 m,500 m),钻孔数据如图4(b)所示,模型二重力张量正演结果如图5所示。
以Vzz的反演为例,通过拟合变差模型,最小化式(24),得到球体变差模型C=5 000 (kg/m3)2,C1=0,ax=300 m,ay=300 m,az=400 m。反演结果如图6所示。
对比图6(a)和图6(b),当反演在水平方向不同埋深、不同密度的两个长方体时,两种方法都能够很好地反演出地下异常的位置,对于反演的密度值,带深度加权的协方差方法反演出的埋深较浅的异常体密度值比埋深较深的异常体密度值大,与初始模型相反,这是由于在模型二的情况下,埋深较深的异常体在地表产生的重力张量异常要比浅部异常体在地表产生重力张量值小。带钻孔数据的协同克里格反演能够准确地确定两个长方体的具体位置和密度值。观察图6(b)至图6(f)可以看出,结合钻孔数据,重力张量各分量反演出来的结果都能较好地确定地下异常体的位置及剩余密度值。

图4 模型二图

图5 模型二重力张量正演结果
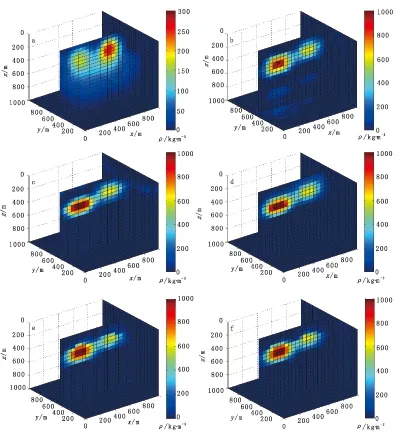
图6 模型二协同克里格反演结果(切片在y=450 m处)
3 结论
作者提出了基于协同克里格法重力张量随机反演,并通过长方体模型验算了协同克里格的反演效果,并得出以下结论:
1)利用协同克里格法能够反演重力张量各分量数据,反演结果能够较好地确定地下异常体的位置。
2)利用带深度加权函数的协同克里格方法反演出来的密度值跟初始模型有偏差,对多个异常体反演时,由于浅部异常的响应,带深度加权函数的协同克里格方法反演出的较深部信息不明显。
3) 利用钻孔数据反演出来的结果能够较好的确定剩余密度值,并且对不同埋深的异常体都能很好地反映。
[1] 王灿,朱自强,鲁光银,等. 重力梯度张量解析信号的正演模拟[J]. 中国有色金属学报,2013,23(9):2479-2497. WANG C, ZHU Z Q,LU G Y,et al. Forward simulation of analytic signals of gravity gradient tensor. The Chinese Journal of Nonferrous Metals, 2013,23(9): 2479-2497.(In Chinese)
[2] LI X, CHOUTEAU M. Three-dimensional gravity modeling in all space[J]. Surveys in Geophysics,1998,19: 339-368.
[3] LI Y G, OLDENBURG D W. 3-D inversion of magnetic data[J]. Geophysics,1996,61(2):394-408.
[4] LI Y G, OLDENBURG D W. 3-D inversion of gravity data[J].Geophysics,1998,63(1):109-119.
[5] ZHDANOV M, ELLIS R, MUKHERJEE S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data[J]. Geophysics,2004, 69(4):925-937.
[6] 王浩然,陈超,杜劲松.重力梯度张量数据的三维反演方法与应用[J]. 石油地球物理勘探,2013,48(3):474-481. WANG H R,CHEN CH,DU J S. 3-D inversion of gravity gradient tensor data and its applications.OGP,2013,48(3): 474-481.(In Chinese)
[7] 陈少华. 基于预条件共轭梯度法的重力梯度张量反演研究[D]. 长沙:中南大学,2012. CHEN SH H. Inversion research of gravity gradient tensor based on preconditioned conjugate gradient.Changsha: Central South University,2012.(In Chinese)
[8] 宋庆磊,杜德文,丁明,等. 协同克里格方法在东海表面温度场数据插值中的应用[J]. 海岸工程,2011,30(3): 49-55. SONG Q L,DU D W,DING M,et al. Application of co-kriging method to interpolation of surface temperature data in East China sea .Coastal Engineering, 2011,30(3):49-55.(In Chinese)
[9] 侯景儒,尹镇南,李维明. 实用地质统计学[M].北京:地质出版社,1998. HOU J R,YIN ZH N,LI W M. Practical geostatistics.Beijing: Geological Publishing House,1998.(In Chinese)
[10]季青,余明. 基于协同克里格插值法的年均温空间插值的参数选择研究[J]. 首都师范大学学报:自然科学版,2010,31(4):81-87. JI Q,YU M. Study on parameters setting of ordinary cokriging interpretation to average annual temperature.Journal of Capital Normal University: Natural Science Edition,2010,31(4): 81-87.(In Chinese)
[11]BOSCH M, MCGAUGHEY J. Joint inversion of gravity and magnetic data under lithologic constraints[J].The leading edge,2001,20:877-881.
[12]BOSCH M, MEZA R, JIMéNEZ R, et al. Joint gravity and magnetic inversion in 3D using Monte Carlo methods[J]. Geophysics, 2006,71(4):153-156.
[13]CHASSERIAU P, CHOUTEAU M. 3D gravity inversion using a model of parameter covariance[J]. Journal of Applied Geophysics, 2003, 52:59-74.
[14]SHAMSIPOUR P, CHOUTEAU M,MARCOTTE D. 3D stochastic inversion of magnetic data[J]. Journal of Applied Geophysics,2011(73): 336-347.
[15]SHAMSIPOUR P, MARCOTTE D, CHOUTEAU M. 3D stochastic inversion of gravity data using cokriging and cosimulation[J]. Geophysics,2010,75(1):I1-I10.
[16]GLOAGUEN E, MARCOTTE E, GIROUX B ET AL. Stochastic borehole radar velocity and attenuation tomographies using cokriging and cosimulation[J]. Journal of Applied Geophysics,2007,62:141- 157.
[17]鲁红英,肖思和,何建军,等. 三维地震资料储层参数建模方法研究——分形协同克里格法[J]. 成都理工学院学报,2002,29(6):694-697. LU H Y,XIAO S H,HE J J,et al. Research of method on reservoir parameters model using 3D seismic data containing rock-fractal cokriging.Journal of Cheng Du University of Technology,2002,29(6):694-697.(In Chinese)
[18]GIROUX B, GLOAGUEN E, CHOUTEAU M. bh_tomo—a Matlab borehole georadar 2D tomography package[J]. Computers and Geosciences,2007,33:126-137.
[19]ASLI M, MARCOTTE D,CHOUTEAU M. Direct inversion of gravity data by cokriging[C].In: Kleingeld, W., Krige, D. (Eds.), 6th International Geostatistics Congress, Cape town. South Africa.2000:64-73.
[20]孙洪泉.地质统计学及其应用[M].徐州:中国矿业大学出版社,1990. SUN H Q. Geostatistics and its application .Xuzhou:China University of Mining and Technology press,1990.(In Chinese)
3D stochastic inversion of gravity tensor based on Cokriging
HUANG Tian-tong, ZHU Zi-qiang*, LU Guang-yin, CAO Shu-jin
(School of Geosciences and Info-Physics, Central South University,Changsha 410083,China)
Gravity tensor is the second derivative of gravitational field. Compared with traditional gravitational exploration, gravity gradient tensor has a better resolution. Cokriging is a common method in geostatistics. In this paper, we applied cokriging to 3D stochastic inversion of each gravity tensor componentdata. Because potential field data have little resolution along the depth direction, we use depth weighting function and borehole data to solve this problem, and we compare the inversion results between both above methods. The inversion results show that the cokriging method can invert each gravity tensor component data. And both methods are capable of inverting the position of causative in the subsurface. In addition inversion results with depth weighting function cannot precisely recovered the anomalous bodies. But incorporating borehole date into inversion can improve the results with better resolution along the depth.
cokriging; gravity tensor; inversion; borehole date; depth weighting function
2014-07-01 改回日期:2014-08-14
国家自然科学基金(41174061,41374120); 中南大学自由探索计划(2011QNZT011)
黄天统(1991-),男,硕士,从事重磁相关领域的研究,E-mail:huang3200101@163.com。
*通信作者:朱自强(1964-),教授,博士,主要从事重磁相关领域的研究,E-mail:13507319431@139.com。
1001-1749(2015)04-0428-09
P 631.1
A
10.3969/j.issn.1001-1749.2015.04.04
