基于磁偶极子模型水平钻进目标定位的算法研究
2015-05-03彭海蛟丁红胜白世武
彭海蛟, 丁红胜, 白世武
(1.北京科技大学 物理系,北京 100083;2.中国石油天然气管道科学研究院,廊坊 065000)
基于磁偶极子模型水平钻进目标定位的算法研究
彭海蛟1, 丁红胜1, 白世武2
(1.北京科技大学 物理系,北京 100083;2.中国石油天然气管道科学研究院,廊坊 065000)
在地下水平定向钻进技术中,为了实现水平定向钻进中的轨迹监控和精确导向,需要实时获取地下钻头的空间位置和姿态参数。这里基于磁偶极子模型下的磁场表达式,推导出采用通电螺线管线圈产生一个类似于磁偶极子的静磁场与时谐场的磁场分布。通过非线性和线性算法,对源端钻头与目标端的距离和相对方位进行定位,从而提高了它们的相对位置的测量精度。同时利用磁定位的非线性算法和线性算法,使其目标误差最小,精度高,速度加快,稳定可靠。
定向钻进技术; 磁偶极子; 螺线管; 磁定位; 定位算法
0 引言
定向对接连通井技术[1]就是利用可溶(燃)性矿产的开采特性,要求一个定向水平井与另一井的靶点或靶井对接连通,采用水平井钻井技术与定向钻探技术,使相距地面数百米的两井或多井,在地下数百米甚至上千米的目标开采处定向实行对接连通,从而来实现两井或多井连通采矿。因此需要建立井口与靶点或者靶井的定向对接井轨迹设计方法,以便及时准确地反映出对接井钻井的要求。
目前几乎所有用磁信号[2-3]来确定目标井钻井轨迹的一些常用方法,一般都是通过建立磁偶极子模型、利用测量出来的大量数据通过反演模型来确定出运动参数和目标位置。最常见的利用磁信号来实现目标定位的三种方法[4]:①利用N个传感器来确定出远场各点处的磁场信号,然后利用最小二乘法等一些参数拟合的算法来实现磁目标定位;②通过埃德森方程及子空间匹配技术,从而估算出目标的运动参数(这种方法必须依赖各种布设的方案);③通过很多更为复杂的测磁仪分别测量单点的磁场和磁场梯度分量,从而实现磁定位。
现阶段国内有很多人针对磁目标定位的一些问题做了大量的研究。王金根等人[5-6]提出了多种定位的方法:最优化定位、基于神经网络定位、函数组合法、 二次差分矩阵法和频谱匹配法等。还有一些常用方法可归结为磁场目标定位常用方法中的前两种[7-10]。
由于实际中没有真正的磁偶极子源,这里分析了采用通电螺线管线圈产生一个类似于磁偶极子[6,11]的磁场分布,致力于前两种方法,基于磁偶极子模型,研究了由源端到目标端的定位算法,通过对其误差函数的分析,提出了一种非线性算法与线性算法来计算出源端的位置参数和方向参数,从而实现目标定位。
1 螺线管线圈的静磁场与时谐场分析
分析长度为L,线径为d的单层密绕螺线管的外部磁场分布。以螺线管中心O点设为原点建立直角坐标系,如图1所示,P点是螺线管外部任意的一点,到O点的距离为r,OP与z轴之间的夹角为,Q点是P点在z轴上的投影。在球坐标系中P点的坐标可表示为(r,θ,φ),而在柱坐标系中可表示为(ρ,φ,Z)。沿螺线管轴方向任意取一段微元dz,P点到该中心的距离为R,P点到该中心螺线管轴方向所成的夹角为δ。若螺线管的载流电流为I,则该微元上通过的电流大小可表示为I·dz/d,于是根据静态磁偶极子物理模型得出载流环的磁场表达式为式(1)。
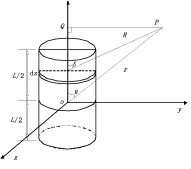
图1 螺线管外部磁场分布示意图
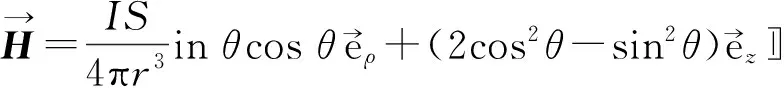
(1)
可得微元在P点处产生的磁场为
(2)
R2=(r2+z2-2rzcosθ)
(3)
式(2)为沿螺线管轴向上的任一微元在P点产生的磁场表达式,在区间(-L/2,L/2)上对该表达式进行积分,即得出螺线管在P点产生的磁场:
(4)
式(4)积分表达式可以分为两部分来进行,记为
(5)
(6)
将δ代入到式(5)与式(6)中积分得式(7)。
(7)
同样可得
(8)
即可得通电螺线管线圈外的磁场分布表达式:
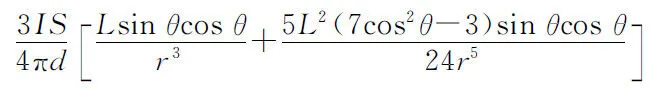
(9)

(10)
式(10)与磁偶极子磁场分布非常类似,只是磁偶极子为一个载流线圈,而单层的密绕螺线管可视为L/d个载流线圈的叠加。因此对于多层密绕螺线管,磁场分布可视为多个磁偶极子的叠加。而螺线管线圈的时谐场表达式除了包含谐变因子外,与静磁场是完全一样的,因此通电螺线管线圈产生的时谐场也就等效于磁偶极子准静态场,通电螺线管线圈的时谐场为:
(11)
2 静态磁偶极子模型
2.1 模型建立和公式推导
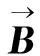
(12)
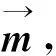
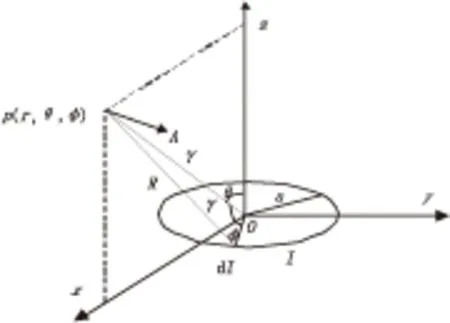
图2 磁偶极子模型
(13)
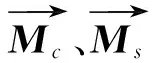
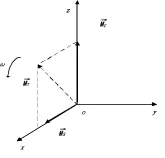
图3 旋转磁偶极子等效示意图
Y轴与近钻头旋转轴向一致,假设钻头旋转速率为ω(rad/s),t时刻后源端旋转过的角度为ωt,则正交磁偶极子等效为:
(14)

2.2 参考场的构造
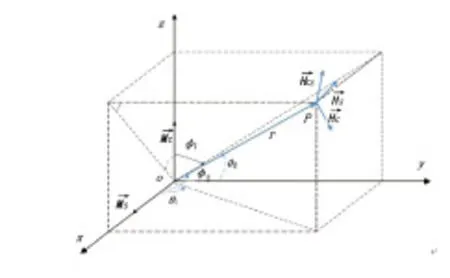
图4 磁场空间传播模型
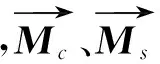

(15)
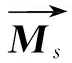
(16)
那么磁偶极子在远场各点处产生的磁场强度为:
式中:φ1为Z轴与OP的夹角,φ2为X轴与OP的夹角,θ1为X轴与P在XY平面上的投影之间角,θ2为Y轴与OP在YZ平面上的投影之间的夹角。

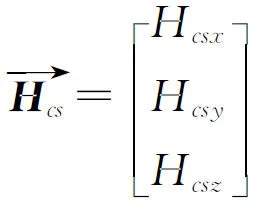
(17)
2.3 特征方位角和相对倾斜角的计算

(18)
将Hcs表达式代入到式(18)得α与φ0之间的关系:
(19)
(20)
由式(20)可算出相对倾斜角θ0因为磁偶极子是跟着源端钻头一起旋转的,而且P点的磁场是被椭圆极化的, 所以P点的磁场强度的最小值与距离r的关系可以表示为式(21)。
(21)
综上可知:旋转磁偶极子空间的坐标P(r,θ0,φ0),可以通过P点的特征磁场信号来确定,由极坐标系与直角坐标系的相互转化关系可得直角坐标(x,y,z), 从而确定源端钻头与目标端的相对位置关系。
通过旋转磁偶极子的高精度导向定位算法计算出源端钻头与目标端的相对位置关系,确定运动轨迹后,得到运动轨迹的倾角范围和位置范围,至少需要六个传感器确定定位定向中得方向参数和位置参数的六个未知参数。定义目标函数和误差函数,通过非线性算法使误差函数值最小,计算最合适的位置参数和方向参数。
3 磁场定位非线性算法与线性算法
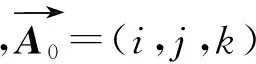
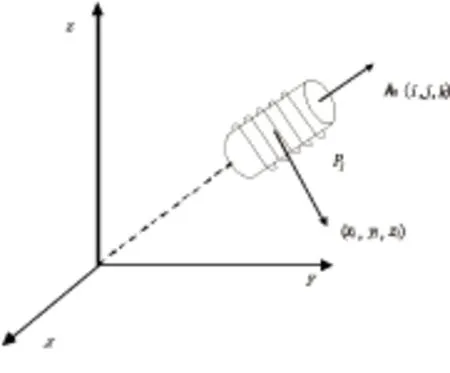
图5 磁场定位坐标系
当螺线管体的尺寸远小于源端与目标端的距离时,即螺线管线圈可以被看作是磁偶极子。由磁偶极子理论表达式(12)可得,螺线管线圈空间某(x1,y1,z1)T点上的磁场强度为:
(22)
i2+j2+k2=1
即磁场强度的三个正交分量可以表示为:
Hlx=HT×
(23)
Hly=HT×
(24)
Hlz=HT×
(25)

3.1 非线性算法
如果要确定六个未知的定位定向的位置参数和方向参数需要N(N≥6)传感器,由于存在噪声、温度、外界环境等因素的干扰,解可能会不唯一,根据以上原因我们定义一个目标函数,通过计算目标函数的最小值来获得定位定向参数的最优解,三个正交分量的磁场强度分别定义误差函数[13]如下:
(26)
(27)
(28)
式(26)、式(27)、式(28)中:N为传感器的数量,N≥6。
总目标误差E=Ex+Ey+Ez
根据上述误差函数,当总目标误差函数E达到最小时,计算出最合适的位置参数(a,b,c)和方向参数(i,j,k),即非线性最小方差求解。由于非线性算法在求解的过程中需要较长时间,为了解决非线算法速度慢的问题,进一步可使用线性算法。
3.2 线性算法
因为在磁定位利用非线性优化算法的过程中有局限性。首先非线性优化算法必须要给提前出一个初值,这样才能计算出最优解,如果给出的一个初值误差比较大时,由于磁偶极子模型存在着局部最优,这样的话非线性算法就很难得到全局最优解;其次利用非线性优化算法准确性不是很好,在整个过程中是需要大量的时间通过各种信号处理的方法来改善跟踪其准确性,而且非线性算法在求解过程中需要时间比较长。而线性算法能够解决上面的所有问题,此算法可以根据绝对矢量运算[14]来推导得到:
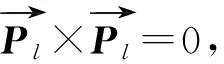
(29)

(30)
即:
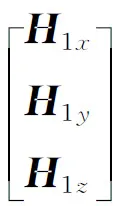
(31)
化简可得:
(H1x,H1y,H1zH1zyl-H1yzl,H1xzl-
(32)
同样可以利用六个三轴传感器,通过这些传感器来选择合适位置组成一个齐次线性方程组,从而计算出最合适的位置参数(a,b,c)和方向参数(i,j,k)。
4 结论
针对定向对接连通井技术的开采特性,为了实现两井或多井连通开采的需要,通过研究通电螺线管线圈产生一个类似于磁偶极子的磁场分布和静态磁偶极子与旋转动态磁偶极子的磁场信号分布规律,提出一种高精度导向定位的算法。利用磁定位的非线性算法与线性算法求解方程组对螺线管线圈进行空间定位。
为了提高目标定位的测量精度,利用磁场强度的三个正交分量定义了误差函数,利用磁定位的非线性算法通过求解方程组来实现定位,由于非线性算法在求最优解的过程中可能很难求得全局最优解和求解时间较长的缺点,为了解决这这些问题,利用磁定位的线性算法,计算位置参数和方向参数来实现定位。非线性算法求最优解需要依赖于初值,初值如果选定好,该算法的精度高,但是运算速度慢,而线性算法求解过程中不依赖于初值,运算速度快,但是该算法的精度低。如果采用线性和非线性算法的综合算法,就能够稳定的、快速地得到精度高的定位结果。
[1] 向军文, 刘春生. 定向对接连通井技术及其新进展 [J]. 中国井矿盐, 2002(1): 20-23. XIANG W J,LIU CH SH. Directional well technology and its development in communication . Chinese mineral salt,, 2002(1): 20-23.(In Chinese)
[2] 其木苏荣, 刘凤敏, 井孝功, 等. 水平层状介质中任意方向磁偶极子的电磁场分布 [J]. 大学物理, 2006(10): 31-36+40. QIMU SH R,LIU F M,JIN X G,et al. Horizontally stratified medium in any direction of the magnetic dipole electromagnetic field distribution . University Physics, 2006(10): 31-36+40.(In Chinese)
[3] 其木苏荣, 赵永芳, 井孝功. 偶极子在径向非均匀介质中的电磁场分布 [J]. 大学物理, 2004(08): 16-19. QIMU SH R,ZHAO Y F,JIN X G. The electromagnetic field in radial inhomogeneous medium distribution . University Physics, 2004(08): 16-19.(In Chinese)
[4] MERLAT L, NAZ P. Magnetic localization and identification of vehicles [C]. International Society for Optics and Photonics, 2003.
[5] 王金根, 龚沈光. 基于运动标量磁强计的磁性目标定位问题研究 [J]. 电子学报, 2002(7): 1057-1060. WANG J G,GONG SH G. Based on magnetic targeting sports scalar magnetometer problem . Acta Electronica, 2002(7): 1057-1060.(In Chinese)
[6] 唐劲飞, 龚沈光, 王金根. 磁偶极子模型下目标定位和参数估计的两种新方法 [J]. 电子学报, 2003(1): 154-157. TANG J F,GONG SH G,WANG J G. Two new parameter estimation method for targeting and lower magnetic dipole model . Journal of Electronics,2003(1): 154-157.(In Chinese)
[7] JIAPENG1 W, ENGINEERING Y Z S O E I, UNIVERSITY T, et al. Video processing and RFID based vehicle detection and identification system[C].China Communication and Transportation Association、American Society of Civil Engineers,2007.
[8] 杨云涛, 石志勇, 关贞珍, 等. 地磁场在导航定位系统中的应用 [J]. 中国惯性技术学报, 2007(6): 686-692. YANG Y T,SHI ZH Y,GUAN ZH ZH,et al. Earth's magnetic field used in navigation and positioning systems . Chinese Inertial Technology, 2007(6): 686-692.(In Chinese)
[9] 张建春, 王传雷. 水下磁性物体探测定位方法研究 [J]. 水运工程, 2009(10): 75-77. ZHANG J CH,WANG CH L.Underwater magnetic object detection and location method . Water Transport Engineering, 2009(10): 75-77.(In Chinese)
[10]边新迎, 李庆民, 李华. 舰船实时磁定位方法研究 [J]. 探测与控制学报, 2006(05): 35-38+55. BIAN X Y,LI Q M,LI H. Real-time magnetic positioning method of ship . Detection & Control, 2006(05): 35-38+55.(In Chinese)
[11]吴旭东, 侯文生, 郑小林, 等. 磁偶极子的定位模型及实验验证 [J]. 仪器仪表学报, 2008(2): 326-329. WU X D,HOU W SH,ZHEN X L,et al. Location magnetic dipole model and experimental verification . Journal of Scientific Instrument, 2008(2): 326-329.(In Chinese)
[12]田雨, 王成林. 有源交变磁场导向定位方法及实验研究 [J]. 电子测量技术, 2011(10): 4-7. TIAN Y,WANG CH L. Active alternating magnetic field oriented positioning method and experimental study . Electronic Measurement Technology, 2011(10): 4-7.(In Chinese)
[13]CHAO H, MENG M Q, MANDAL M. Efficient magnetic localization and orientation technique for capsule endoscopy[C], 2005. 2-6 Aug. 2005.
[14]HU C, MENG M-H, MANDAL M. A linear algorithm for tracing magnet position and orientation by using three-axis magnetic sensors [J]. Magnetics, IEEE Transactions on, 2007, 43(12): 4096-4101.
Algorithm study based on the magnetic dipole model on horizontal drilling target positioning
PENG Hai-jiao1, DING Hong-sheng1, BAI Shi-wu2
(1.Department of Physics, University of Science and Technology Beijing, Beijing 100083, China;2.Pipeline Research Institute of China National Petroleum Corporation, Langfang 065000, China)
In underground horizontal directional drilling technology, it needs to obtain the underground spatial position and posture parameters of the drill in real time to implement the horizontal directional drilling trajectory monitoring and precise orientation. Therefore, based on the magnetic field expression of the magnetic dipole model, the magnetic field distribution which is similar to the static magnetic field and the time-harmonic field of the magnetic dipole are deduced by using electric solenoid coil. To achieve positioningby means of the arithmetic of the relative orientation and the distance between the drill and the objective targets, the measurement accuracy of the relative position can be improved. In the mean time wetake advantage of the linear and nonlinearmethods of the magnetic localization to make the smallest target error,high precision, much more speed, stable and reliable.
horizontal directional drilling; magnetic dipole; solenoid; magnetic location; location algorithm
2014-08-12 改回日期:2014-11-04
国家自然科学基金资助(61072082);中央高校基础科研业务费(FRF-MP-12-008A)
彭海蛟(1987-),男,硕士,从事重磁方法研究,E-mail: penghaijiao1224@163.com。
1001-1749(2015)04-0422-06
P 631.2
A
10.3969/j.issn.1001-1749.2015.04.03
