基于OpenMP的一阶声波方程波场并行算法

方金伟， 白洪涛， 孙惠敏

(1. 吉林大学 a.地球探测科学与技术学院, b.公共计算机教学与研究中心, 长春 130012)



基于OpenMP的一阶声波方程波场并行算法

方金伟1a， 白洪涛1b*， 孙惠敏1a

(1. 吉林大学 a.地球探测科学与技术学院, b.公共计算机教学与研究中心, 长春 130012)

针对高阶交错网格技术的计算效率瓶颈，研究了一种基于OpenMP的一阶声波方程波场并行算法。通过对多组不同规模的模型测试，分析了并行效率在不同并行粒度下模型和CPU核心数目的关系。实验结果表明，该方法达到了与串行方法相同的数据精度，在微机商用多核CPU上获得了2倍多的性能提升。

一阶声波方程; 高阶交错网格; OpenMP; 并行效率

0 引言

地震波场数值模拟是一种研究复杂地区地震资料的有用手段。常见的波场模拟的方法：有限差分法、有限元法和伪谱法等，其中有限元法精度高，但计算量大，对计算机的内存要求高；有限差分法计算速度较快，占用内存小，编程相对简单，而且通过加密网格可以很好地压制频散效应，是目前应用最广泛的方法。凭借着一阶速度-应力弹性波方程无需对弹性常数进行空间微分的优点，所以此类波动方程在弹性波波场模拟中常被使用。交错网格技术最早由Madariaga R[1]提出，Virieux在同性介质正演中用到的差分精度为o(Δt2+Δx2)的交错网格，其相比于常规网格，在计算精度和效率均有所提高。Levande[4]把这种差分网格的精度进一步提高到了o(Δt2+Δx4)。Dablain[5]提出了高阶差分方法，解决了声波方程求解的精度和效率的矛盾。随后，Crase[6]又在求解二阶弹性波方程中用到了该方法。高阶差分可以通过选取合适的时间和空间阶数，采用空间的阶数高于时间的阶数的差分形式，既可以保证较高的计算精度，而且计算效率可以得到一定的提高，另外，可以选取尽可能大的空间步长，在保证精度的前提下，获得效率的提升。其后很多学者又对其进一步发展，董良国等[7]给出了一阶交错网格高阶差分解法，并详细讨论了其稳定性条件；刘洋等[8]从Taylor级数展开式出发，推导出任意阶导数的任意偶数阶精度差分格式，并给出相应差分系数的公式。高阶交错网格有限差分理论有很高的差分精度，但其计算效率还有一定的提升空间，这里将结合现代微机CPU多核技术，来提高该方法的实际计算效率。

在现有的工艺条件下，摩尔定律限制了通过提升指令的吞吐量和时钟速度来改善CPU性能的方法，故超线程、多核技术和计算机的缓存等技术孕育而生，尤其在微型商用机芯片中使用较多，多核技术更为瞩目。AMD、Intel等主要微机CPU厂商通过从提高主频转向整合多个核心引擎，来改变处理器的性能。目前常见的多核多线程开发工具有pThreads库、Win32 线程库以及OpenMP等。pThreads库是Linux下最常用的多线程支持库，Windows操作系统也有其移植版pthreads-win32，它具有很好的可移植性，但使用难度比较大；Win32 线程库拥有完善而复杂的函数库，目前比较成熟，但对编程人员有较高的要求；OpenMP用于共享内存并行系统的多线程程序设计的一套指导性的编译处理方案，降低了并行编程的难度和复杂度，灵活性强易使用。目前支持多线程开发工具OpenMP的有：MicrosoftVisualStudio、IntelC++编译器。OpenMP在并行在细粒度与粗粒度技术[9]上均具有很高的计算效率。这里采用一阶声波方程进行交错网格高阶差分方法模拟计算均匀层状介质波场，通过OpenMP并行化，测试不同模型下的不同粒度的并行效率。

1 一阶声波方程交错网格高阶差分方法

1.1 一阶声波方程

在不考虑体应力的情况下，二维一阶声波方程具体形式为式(1)：

(1)

其中：K=pv2为体积模量；v为纵波速度；vx为x方向上的速度分量；vz为z方向上的速度分量；p为声压；ρ为密度。

1.2 高阶有限差分原理

空间上2N阶差分，运用导数的高阶展式，

(2)

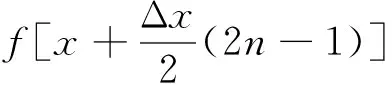
(3)

时间上2M阶差分原理如公式(4)所示：

(4)

其中:Δt为时间步长。

1.3 边界吸收

有限差分数值模拟中常采用完全匹配层(PML)边界吸收条件[10]，即在边界处加一匹配层，采用衰减效应的波动方程，通过改变阻尼因子来控制边界反射吸收的效果。常规的PML吸收条件针对一阶波动方程，将波场分裂成沿着垂直和平行于传播方向的两组，在人工边界处使得平行界面法向传播的平面波快速衰减，对其他方向波场不衰减，从而边界吸收的目的。对于一阶声波方程，只对声压分量进行分裂，因为速度分量是声压分量对相应的坐标轴的一阶空间导数。声压可以分解为px、pz两个部分，如公式(5)所示。

p=px+pz

(5)

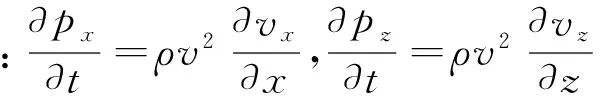
对应的边界吸收方程为公式(6)。

(6)

速度边界吸收方程为公式(7)：

(7)

其中： d(x)=-1.5vmaxlog(R)x2/δ3； d(z)=-1.5vmaxlog(R)z2/δ3；vmax为最大纵波速度；δ为匹配层厚度；R为理想状态下介质的反射系数。

1.4 稳定性条件

二维交错网格高阶有限差分格式的稳定性条件[11]，可由傅里叶分析方法可得到，其公式为式(8)。

(8)

式(8)中：vmax为最大纵波速度；Δt为时间采样间隔；Δx、Δz分别为x、z两个方向的网格间距。

2 基于OpenMP的并行化

2.1 并行算法流程

我们通过运用一阶速度-应力弹性波方程为波动方程，使用时间上二阶，空间八阶的交错网格，采用阻尼衰减对网格边界处理，对水平层状介质进行波场计算，并行程序的算法流程如图1所示。

2.2 程序算法正确性对比

通过不同模型的串行和并行算法分别得到波场记录(图2、图3)。图2是模型(800×1 200×800)的串行和细粒度并行结果对比；图3是模型(800×1 200×2 000)的串行和粗粒度并行结果对比。

由图2、图3可以看出，无论在细粒度还是粗粒度，并行算法获得与串行算法完全相同的计算结果。

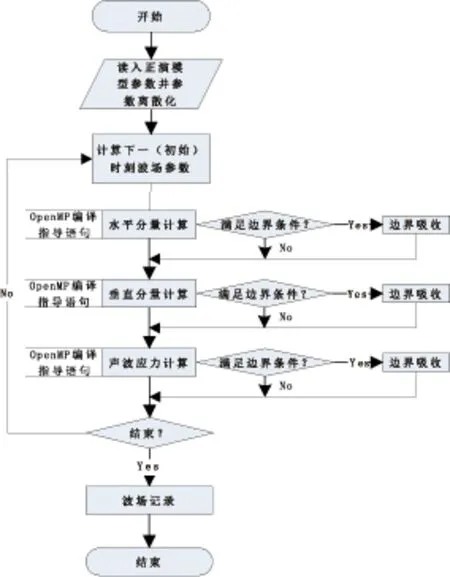
图1 波场并行算法流程图

图2 细粒度串、并行结果

图3 粗粒度串、并行结果

2.3 并行效率分析

通过进行多组模型的测试，从加速比和并行效率两方面来讨论并行算法的效率。测试平台为CPU 4核心, 主频1.5 GHz，集成开发环境Visual Studio 2010。

从表1可以看出，在细粒度并行情况下(当核心数目为1时，为串行结果)，随着核心数目的增加，加速比有较大的变化，当核心数目为3时，加速比最大，加速效率在两倍以上；随着模型的改变，加速比总体呈现增加的趋势。

从表2可以看出，在粗粒度并行情况下，随着核心数目的增加，加速比有大的变化，但总体上当核心数目为3时，加速比最大，且比细粒度下的加速比大；随着模型的改变，加速比并没有体现递增趋势。

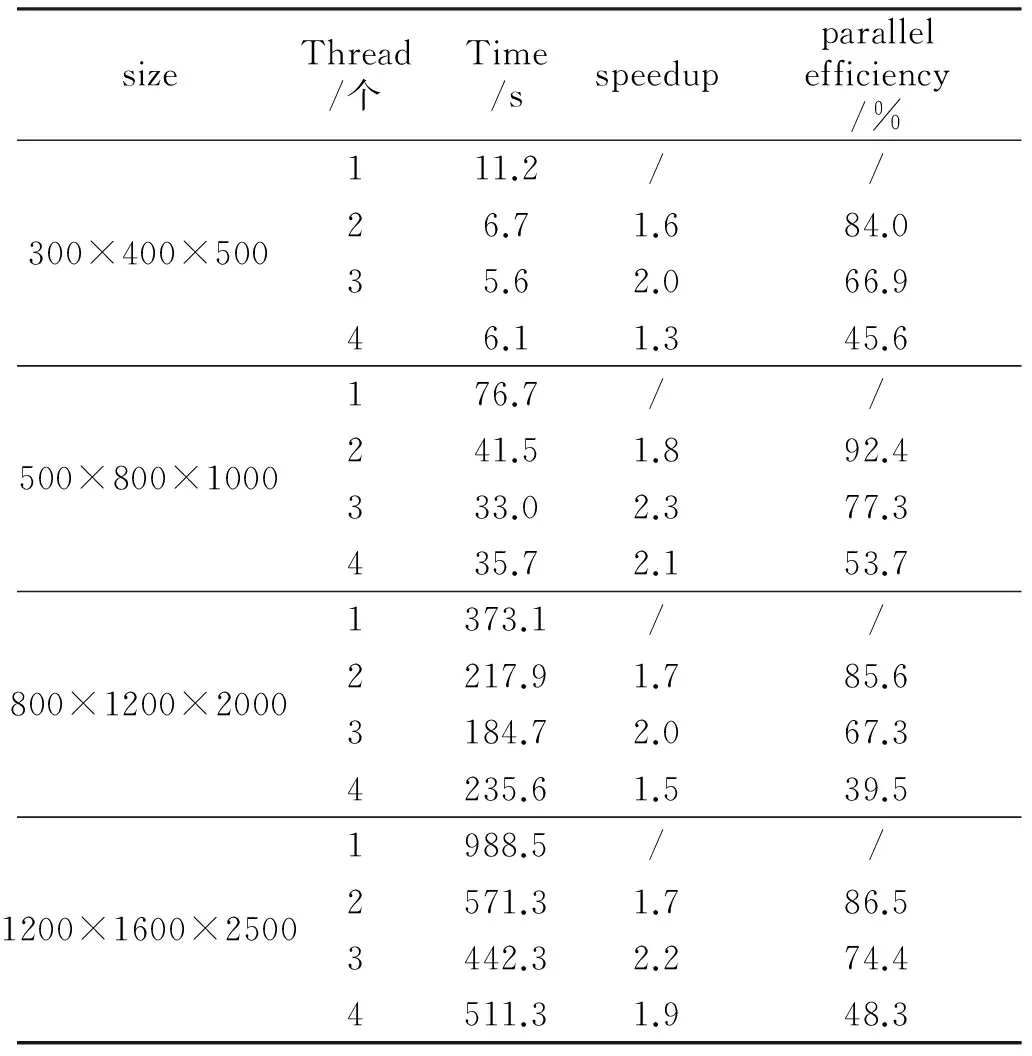
表1 细粒度并行不同模型的测试结果

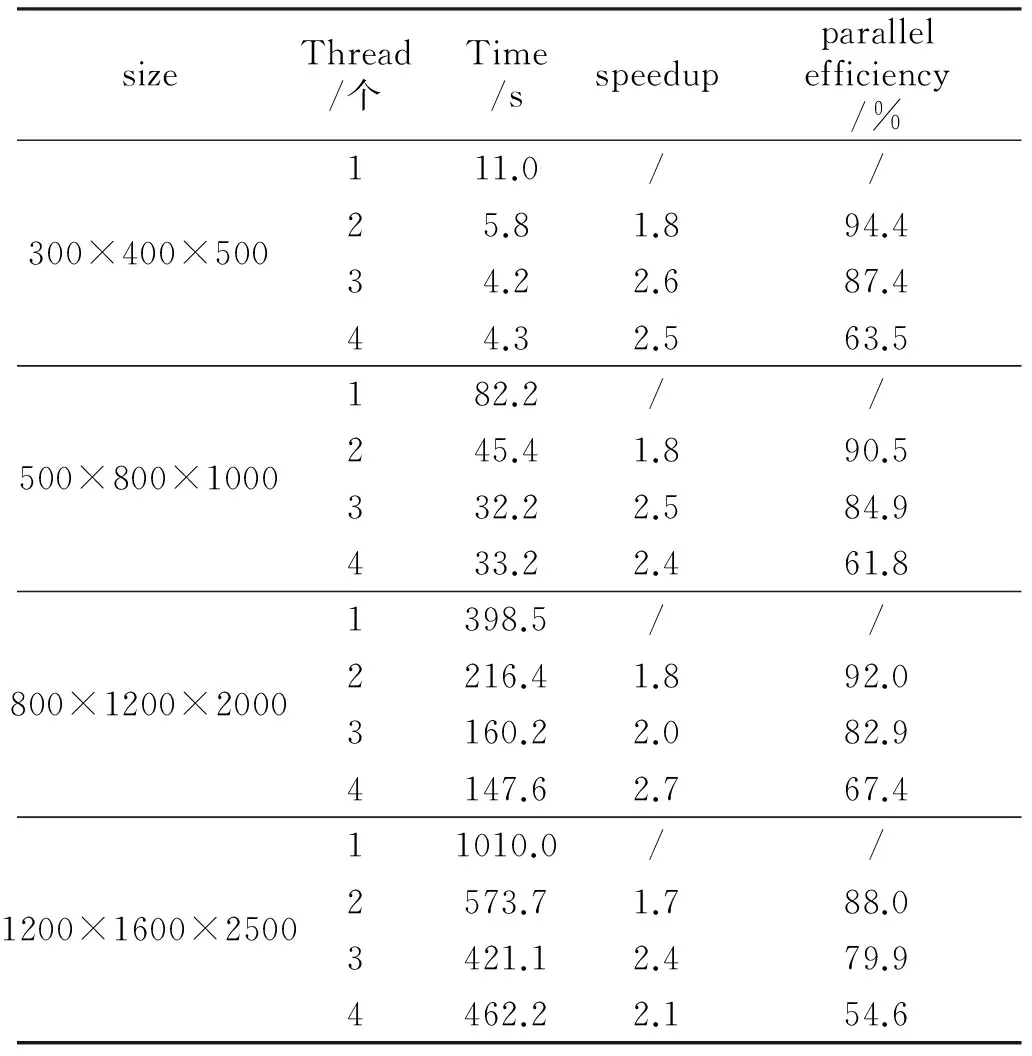
表2 粗粒度并行不同模型的测试结果

3 结论

采用了基于多核多线程技术，实现了基于OpenMP的一阶声波方程高阶有限差分数值并行模拟计算。在保证计算结果正确可靠的前提下，获得了较高的并行计算效率。作为一种简单又实用的技术，OpenMP具有可以跨平台、跨语言使用的特点，在波场模拟及一系列计算比较大量数据预算中使用，可以提高效率，从而缩短计算时间。

这里基于均匀层状介质的波场模拟计算，有望于在复杂介质中应用OpenMP技术探究其加速效果；另外，在地震记录中，往往多炮记录间有并行化处理，但在单炮记录中少见并行算法，所以在地震单炮记录的数据处理中有一定的应用空间。

[1] MADARIAGA R. Dynamics of an expanding circular fault[J]. Bulletin of the Seismological Society of America, 1976, 66(3): 639-666.

[2] VIRIEUX J. SH-wave propagation in heterogeneous media: velocity-stress finite-difference method[J]. Geophysics, 1984, 49(11): 1933-1942.

[3] VIRIEUX J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method[J]. Geophysics, 1986, 51(4): 889-901.

[4] LEVANDER A R. Fourth-order finite-difference P-SV seismograms[J]. Geophysics, 1988, 53(11): 1425-1436.

[5] DABLAIN M A. The application of high-order differencing to the scalar wave equation[J]. Geophysics, 1986, 51 (1): 54-66.

[6] CRASE E.High-order (space and time) finite-difference modeling of the elastic wave equation. 60th SEG meeting, San Francisco, USA[J]. Expanded Abstracts, 1990,987-991.

[7] 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419. DONG L G,MA Z T,CAO J ZH,et al. The staggered-grid high-order difference method of one-order elastic equation. Geophys, 2000,43(3):411-419.(In Chinese)

[8] 刘洋, 李承楚, 牟永光. 任意偶数阶精度有限差分法数值模拟[J]. 石油地球物理勘探, 1998,33(1):1-11. LIU Y, LI CH CH, MOU Y G. Finite-difference numerical modeling of any even-order accuracy.OGP, 1998,33(1):1-11.(In Chinese)

[9] 白洪涛. 基于GPU的高性能并行算法研究[D].长春:吉林大学, 2010. BAI H T. Research on high performance parallel algorithms based on GPU. Changchun: Doctoral Dissertation of Jilin University, 2010.(In Chinese)

[10]王永刚, 邢文军, 谢万学, 等. 完全匹配层吸收边界条件的研究[J]. 中国石油大学学报: 自然科学版, 2007, 31(1): 19-24. WANG Y G, XING W J, XIE W X, et al. Study of absorbing boundary condition by perfectly matched layer. Journal of China university of petroleum:natural science, 2007, 31(1): 19-24.(In Chinese)

[11]董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报, 2000, 43(6): 856-864. DONG L G, MA Z T, CAO J ZH. A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation. Geophysics, 2000, 43(6): 856-864.(In Chinese)

[12]黄易, 师学明, 范建柯, 等. 并行计算技术及其在勘探地球物理学中的现状与展望[J]. 地球物理学进展, 2010,25(2): 642-649. HUANG Y, SHI X M, FAN J K, et al. Review on parallel computing and its application in exploration geophysics. Progress in Geophys, 2010, 25(2): 642-649.(In Chinese)

[13]杜增利, 李亚林, 尹成, 等. 虚谱法一阶应力-速度方程地震数值模拟[J]. 石油地球物理勘探, 2009, 44(5): 637-641. DU Z L,LI Y L,YIN CH, et al. Pseudo-spectral method seismic numerical modeling of first-order stress-velocity equation. OGP, 2009, 44(5): 637-641.(In Chinese)

[14]牟永光, 裴正林. 三维复杂介质地震数值模拟[M].北京:石油工业出版社, 2005. MOU Y G, PEI ZH L. Seismic numerical modeling for 3-D complex media. Beijing: Petroleum Industry Press, 2005.(In Chinese)

[15]潘海滨. 交错网格地震波场模拟及频散校正策略[J]. 物探化探计算技术, 2009, 31(4): 369-373. PAN H B. Staggered-grid seism wave IC wave simulation and the correction of numerical disperse. Computing Techniques for Geophysical and Geochemical Exploration, 2009, 31(4): 369-373.(In Chinese)

[16]李振春, 张慧, 张华. 一阶弹性波方程的变网格高阶有限差分数值模拟[J]. 石油地球物理勘探,2008.43(6):711-718 LI ZH CH, ZHANG H, ZHANG H. Variable grid high order finite difference numeric simulation of first order elastic wave equation. OGP, 2008,43(6):711-718.(In Chinese)

[17]宁刚, 熊章强, 陈持逊. 波动方程有限差分正演模拟误差来源分析[J]. 物探与化探, 2008, 32(2): 203-206. NING G, XIONG ZH Q, CHEN CH X. An analysis of the error source in the wave propagation forward numerical simulation. Geophysical and Geochemical Exploration, 2008, 32(2): 203-206.(In Chinese)

A parallel algorithm of wave field using first-order acousticwave equation based on OpenMP

FANG Jin-wei1a， BAI Hong-tao1b*, SUN Hui-min1a

(1. Jilin University, a.College of Geo-Exploration Science and Technology,b.Center for Computer Fundamental Education, Changchun 130012, China)

The implementation of wave field forward modeling parallel computing algorithm is achieved using first-order acoustic wave equation based on OpenMP in this paper, aiming to getting a higher efficiency in comparison with that was in technique of the high-order staggered grid. The relationship between the number of cores and parallel efficiency is analyzed in changing models. The experiments demonstrate that our parallel algorithm can not only acquire the effective data accuracy, but also gain at least two times than the serial version in the multi-core CPU of commercial computer.

first-order acoustic wave equation; high-order staggered grid; OpenMP; parallel efficiency

2014-09-15改回日期：2014-11-25

国家自然科学基金(61272208)；中央高校基本科研业务费专项资金(JCKY-QKJC47,JCKY-QKJC49)；吉林省科技发展计划项目基金(201101039)

方金伟(1991-)，男，本科，主要研究波场正演模拟和参数反演，E-mail：fangjw2311@mails.jlu.edu.cn。

*通信作者：白洪涛(1975-)，男，博士后，主要从事高性能计算研究，E-mail：baiht@jlu.edu.cn。

1001-1749(2015)05-0622-06

P 631.4

A

10.3969/j.issn.1001-1749.2015.05.13