基于时间和空间方向差分稀疏约束的叠前AVO反演

马彦彦， 周 辉， 张洪礼

( 中国石油大学(北京) 油气资源与探测国家重点实验室, 北京 102249)



基于时间和空间方向差分稀疏约束的叠前AVO反演

马彦彦， 周 辉， 张洪礼

( 中国石油大学(北京) 油气资源与探测国家重点实验室, 北京 102249)

在叠前AVO反演中，常规的吉洪诺夫正则化方法不能突出异常体在纵向上的边界，并且忽略了地层的横向联系，导致反演结果产生边缘模糊现象。为了解决这一问题，这里基于Zeoppritz方程的Fatti近似公式和贝叶斯理论框架，以模型参数柯西分布作为先验约束，通过引入时间和空间方向的差分稀疏约束保护地层边界，并最终采用迭代重加权最小二乘算法实现纵、横波阻抗的同时多道反演。模型反演结果具有明显的地层边界和分层特征，表明该方法能够解决边缘模糊问题、保护不连续体的横向边界，大大提高了油气预测的准确度。

叠前AVO反演； 差分稀疏约束； 边界； 同时多道反演

0 引言

地震叠前AVO反演方法能够利用不同入射角度叠加数据和测井数据，得到直接反映储层岩性、物性参数的多种弹性参数，提高预测精度，日渐成为储层预测的主流方法之一。然而由于地震数据频带的限制，以及噪声、正演近似等因素的影响，导致该反演方法高度不适定[1]。许多学者通过在目标函数中引入先验信息作为正则化约束，例如吉洪诺夫正则化方法，以提高反演问题的稳定性。但是这种正则化方法常常会模糊地层岩性发生变化的位置和地质构造的边界等。随着石油勘探开发逐渐向隐蔽油气藏，特别是向砂岩油气藏方向转变，迫切需要准确刻画砂体的空间分布特征。因此研究基于边缘保护的反演方法能够更好地识别岩性，描述砂体分布。

边缘保护的思想最早起源于图像处理领域，主要采用全变分作为正则化约束项[2-3]。近年来，许多学者开始将该思想引入地球物理领域，采用边缘保护方法准确描述地下地质构造。Valenciano等[4]在柯西约束下运用边缘保护正则化方法进行层速度估计；Youzwishen等[5]在叠后地震资料中运用边缘保护正则化算法来估计纵波速度；Zhang等[6]提出一种自适应波阻抗模型重建方法，通过直接引入先验波阻抗信息和声波测井信息作为绝对约束，间接得到能够表征地层、断层等地质构造特征的相对约束的方式，解决叠后波阻抗反演的不适定及带宽有限问题；张赛民[7]应用似柯西分布函数作为正则化项，开展了基于边界保持块约束的叠后波阻抗反演和叠前AVA三参数同步反演研究；Anagaw等[8]提出一种基于边缘保护的地震成像方法，能够同时检测地层结构的纵向、横向不连续问题；Guitton[9]通过在全波形反演中引入块状正则化约束，获得块状速度模型，消除照明和反演假象，由于对速度模型采用水平导数稀疏约束，该方法还可以衰减高频噪声；Yuan等[10]基于反演的思想，以柯西分布作为先验分布，在贝叶斯理论框架下研究了边缘保护随机噪声衰减方法，取得了良好的效果；Tian等[11]以马尔科夫随机场的吉布斯分布形式作为先验约束，用Huber函数作为吉布斯分布的能量函数，在地层边缘得到保护的前提下反演纵波速度、横波速度和密度三个参数；Yuan等[12]提出了保构造的三维同时多道波阻抗反演方法，能够稳定地震反演，减小高波数噪声对反演结果的影响，探测地质构造的空间连续性，提升了现有地震波阻抗反演方法的精度。

常规的在叠前反演目标函数中引入的吉洪诺夫正则化约束存在一定的局限性：①该方法为时间方向全局光滑，不能突出异常体在纵向上的边界；②该方法忽略了地层结构的横向联系；③会受高波数噪声的影响。为了解决边缘模糊问题，同时保持抗噪作用，作者基于Zeoppritz方程的Fatti近似公式，从贝叶斯理论框架出发，以柯西分布作为先验约束，基于边界保持的思想，同时引入时间和空间方向差分稀疏约束，反演纵、横波阻抗，为储层预测和流体识别提供可靠数据。

1 方法原理

1.1 叠前正演公式

Zoeppritz方程的Fatti近似方程式[13]可表示为

R(θ)=(1+tan2θ)Rp-8γ2sin2θRs- (tan2θ-4γ2sin2θ)Rρ

(1)

根据Walker等的研究[14]，在反射系数小于0.3的情况下，反射系数可以用波阻抗对数表示。令模型参数

m=[lnZp,lnZs,lnρ]T，

其中：Zp、Zs、ρ分别为纵波阻抗、横波阻抗和密度向量。

根据Buland(2003)的研究[15]，可将正演地震记录的褶积过程表示为式(2)。

d=Gm=WADm

(2)

其中：W为子波褶积矩阵，A为Fatti近似方程式(1)中与角度有关的系数矩阵，D为纵向上的一阶差分矩阵。

因此地震记录与模型参数的关系可表示为

(3)

以叠前三参数同步反演为例，假定待反演的参数维度为N×M(M为道数，N为每道采样点数)，如果参与反演的角度道集个数为K，则式(2)中，观测数据d的维度为KN×M，正演算子矩阵G的维度为KN×3N，模型参数矩阵m的维度为3N×M。

1.2 基于时间和空间方向差分稀疏约束的叠前AVO反演

由前文可知，含噪地震记录可表示为式(4)。

d=Gm+n

(4)

其中：d=[d1,d2,…,dK]T为观测地震数据；G=WAD为正演算子；m=[lnZp,lnZs,lnρ]T为包含纵波阻抗、横波阻抗及密度三个分量的模型参数矩阵；n为观测噪声。

基于随机变量表达形式的贝叶斯公式可表示为式(5)。

p(m|d)∝p(m)p(d|m)

(5)

其中:p(m)表示模型参数m的先验概率分布；后验概率分布p(m|d)描述了对于给定观测数据d，模型参数的概率；p(d|m)为似然函数，描述观测数据与理论模型之间的差异。

假定噪声服从高斯分布，方差为σ2。若噪声不相关且均值为零，并假设每种噪声样本的方差为常数，则噪声向量的总概率为式(6)。

(6)

似然函数可以用噪声的概率分布表示，又n=d-Gm，则似然函数为式(7)。

(7)

对于地下地层而言，纵向波阻抗是稀疏的，具有明显的分块特征。当地层横向连续性较好时，可认为相邻地震道的波阻抗差值接近于“0”；当地层存在断层、尖灭、裂隙等地质构造时，会导致地震同相轴产生错断，在构造边界处，相邻地震道的波阻抗差值不再为“0”。因此可认为地层横向波阻抗差值是稀疏的。为此定义两个方向性一阶差分算子，其中水平(空间)方向记为C1，时间方向记为C2，具体可表示为如下稀疏阵形式：

(8)

(9)

假设模型参数m服从柯西分布，则其先验概率为式(10)。

(10)。

其中：μ为尺度因子。

最终，后验概率的表达式为式(11)。

(11)

给定后验概率分布p(m|d)，求取模型参数最常用的方式为寻找使得p(m|d)最优的最大后验概率估计，方程(5)改写为式(12)。

(12)

略去常数项，则最大化后验概率函数等价于使得式(13)最小。

(13)

其中：λ=2σ2。式(13)可表示为以下一般形式：

J=J0+λJm

(14)

其中：第一项J0反映了模型参数与正演算子合成地震记录与实际地震记录的相近程度；第二项Jm为模型参数约束项，基于柯西分布先验约束，通过引入横向约束和纵向约束，起到了边缘保护的作用。λ为加权因子，控制模型参数稀疏特征对反演结果的贡献。

对式(13)目标函数J求导，并令其等于零，得到

GT(Gm-d)+λCTQCm=0

(15)

显然，式(15)属于非线性求解问题，Youzwishen指出,对于这类问题可以采用迭代重加权最小二乘算法求解[16]。

2 例子

根据式(3)所示地震记录褶积过程及式(13)所示目标函数，这里采用Marmousi2局部模型进行方法测试。如图1所示，该局部模型地质构造复杂，速度变化剧烈，纵向上分块性较明显，发育许多薄层，横向上具有明显的地质构造边界，发育一条倾斜生长断层(黑色箭头)以及一个不整合面(红色箭头)，存在地层尖灭(椭圆区域)等地质现象，有利于检验本文方法的边缘保护作用。

地震观测数据采用合成记录方式得到。首先利用Fatti近似公式得到反射系数，然后将其与地震子波褶积，得到角度域合成记录。采用的地震子波为主频35Hz的零相位雷克子波，共生成5°、10°、15°、20°、25°五个角度的共角度域道集。

反演参数的低频信息对反演结果具有重要影响，有利于解决反演多解性问题，文本将低频信息作为初始模型代入求解公式。对图1所示真实模型进行0Hz～10Hz的带通滤波，得到待反演参数的低频初始模型如图2所示。

基于稀疏柯西分布先验信息约束，通过在反演目标函数引入横向空间约束C1和纵向时间约束C2，保护地层边界信息。在计算过程中，涉及到加权因子的选取问题，该值的大小主要通过试验的方法求取。

图3为不加约束项，即约束项权重为λ=0时的纵波阻抗、横波阻抗反演结果。与图1对比可以看出，反演结果的边界模糊，观察不到地层尖灭特征，横波阻抗反演结果剖面上几乎无法识别断层的断点位置(黑色箭头所指)。此外，对模型下方500ms以下的倾斜地层而言，未加边缘保护约束项时，反演方法几乎完全不能恢复其地层形态。

图4是选取最优边缘保护约束项权重时的纵波阻抗、横波阻抗反演结果。与图1、图3进行对比可以看出，反演结果得到很大改善，横向上的断层边界(黑色箭头所指)及地层尖灭(黑色椭圆所示)、纵向上的地层界面刻画地更加清楚，薄层(枚红色箭头所指)也得到很好恢复。

为了验证方法的抗噪性，对含噪合成记录进行反演测试。在合成的五个角道集地震记录中加入全频带随机噪声，研究约束项对于噪声压制及边缘保护的作用。加入的噪声占地震记录能量的20%。图5为最终反演结果，尽管较图4反演结果分辨率有所降低，但依然较好地保持了构造边界，地层尖灭、薄层等细节得到了较好恢复。

图1 Marmousi2真实模型局部显示

图2 初始模型

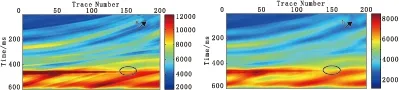
图3 无边缘保护时反演结果

图4 边缘保护反演结果

图5 含20%噪声时边缘保护反演结果

3 结论

作者提出了一种基于时间和空间方向的差分稀疏约束叠前AVO反演方法。该方法以模型参数柯西分布作为先验信息，通过引入纵向上的块约束和横向上相邻道之间的约束，实现同时多道叠前阻抗反演，解决常规正则化约束叠前方法带来的边缘模糊问题，能够保护地层的纵向边界，描述地层的横向连续性，刻画地质构造、地层岩性在横向上的边界。对模型资料进行反演处理，验证了该方法的反演效果和稳健性。

[1] 杨培杰, 印兴耀. 非线性二次规划贝叶斯叠前反演[J]. 地球物理学报,2008, 51(6):1876-1882.YANGPJ,YINXY.Non-linearquadraticprogrammingBayesianprestackinversion[J].ChineseJournalofGeophysics, 2008, 51(6): 1876-1882.(InChinese)

[2]GEMAND,REYNOLDSG.Constrainedrestorationandtherecoveryofdiscontinuities[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1992, 14(3): 367-383.

[3]BOUMANC,SAUERK.AgeneralizedGaussianimagemodelforedge-preservingMAPestimation[J].IEEETransactionsonImageProcessing, 1993, 2(7): 296-310.

[4]VALENCIANOAA,BROWNM,GUITTONA,etal.Intervalvelocityestimationusingedge-preservingregularization[C].The77thAnnualInternationalMeeting,SEG,ExpandedAbstracts, 2004, 2431-2434.

[5]YOUZWISHENCF,SACCHIMD.Edgepreservingimaging[J].JournalofSeismicExploration, 2006, 15: 45-58.

[6]ZHANGHB,SHANGZP,YANGCC.Adaptivereconstructionmethodofimpedancemodelwithabsoluteandrelativeconstraints[J].JournalofAppliedGeophysics, 2009, 67: 114-124

[7] 张赛民. 基于边界保持块约束叠后波阻抗及叠前AVA三参数同步反演研究[D]. 湖南: 中南大学, 2011.ZHANGSM.Researchofpost-stackimpedanceinversionandAVAThree-termSimultaneousInversionbasedonedgepreservingblockyconstrain[D].Hunan:CentralSouthUniversity, 2011.(InChinese)

[8]ANAGAWAY,SACCHIMD.Edge-preservingseismicimagingusingthetotalvariationmethod[J].JournalofGeophysicsandEngineering, 2012(9): 138-146.

[9]GUITTONA.Blockyregularizationschemesforfull-waveforminversion[J].GeophysicalProspecting, 2012, 60: 870-884.

[10]YUANSY,WANGSX.Edge-preservingnoisereductionbasedonBayesianinversionwithdirectionaldifferenceconstraints[J].Journalofgeophysicsandengineering, 2013, 10(2): 25001-25010.

[11]TIANYK,ZHOUH,CHENHM,etal.Bayesianprestackseismicinversionwithaself-adaptiveHuber-Markovrandom-fieldedgeprotectionscheme[J].AppliedGeophysics, 2013, 10(4): 453-460.

[12]YUANSY,WANGSX,LUOCM,etal.Simultaneousmultitraceimpedanceinversionwithtransform-domainsparsitypromotion[J].Geophysics, 2015, 80(2): 71-80.

[13]FATTIJL,SMITHGC,VAILPJ,etal.DetectionofgasinsandstonereservoirsusingAVOanalysis:a3DSeismicCaseHistoryUsingtheGeostackTechnique[J].Geophysics, 1994, 59(9): 1362-1376.

[14]WALKERC,ULRYCHTJ.Autoregressiverecoveryoftheacousticimpedance[J].Geophysics, 1983, 48(10): 1338-1350.

[15]BULANDA,OMREH.BayesianlinearizedAVOinversion[J].Geophysics, 2003, 68(1): 185-198.

[16]YOUZWISHENCF.Non-linearsparseandblockconstraintsforseismicinversionproblems[D].Alberta:UniversityofAlberta, 2001.

Prestack AVO inversion with space and time directional difference sparse constraints

MA Yan-yan, ZHOU Hui, ZHANG Hong-li

(China University of Petroleum, State Key Laboratory of Petroleum Resource and Prospecting, Beijing 102249, China)

In seismic prestack AVO inversion, the conventional Tikhonov regularization method can not highlight the vertical edge of geologic anomalies and usually ignores the lateral connection of strata, which will cause fuzzy edges in inversion results. To address this issue, based on the Fatti approximate formula of Zeoppritz equation and Bayesian framework, this paper introduces the space and time directional difference sparse constraints expressed by the Cauchy norm to protect edges, and realizes the simultaneous multitrace inversion of P-impedance and S-impedance with iteratively reweighted least squares algorithm. The inversion results for model have obvious stratigraphic edge and layered characteristics, and it indicates that the new method can solve the edge fuzzy problem, protect the lateral edge of discontinuities, and largely improve the accuracy of predicting reservoirs.

prestack AVO inversion; difference sparse constraint; edge; simultaneous multitrace inversion

2015-07-14改回日期：2015-08-03

国家自然科学基金项目(41174117)

马彦彦(1983-)，女，博士，主要研究方向为地震资料处理及储层预测，E-mail：cup_mayanyan@163.com。

1001-1749(2015)05-0616-06

P 631.4

A

10.3969/j.issn.1001-1749.2015.05.12