无界区域R1上的非线性梁方程的全局吸引子*
2015-05-02姜金平张晓明
姜金平, 张晓明
(延安大学 数学与计算机科学学院,陕西 延安 716000)
无界区域R1上的非线性梁方程的全局吸引子*
姜金平, 张晓明
(延安大学 数学与计算机科学学院,陕西 延安 716000)
研究了无界区域R1上的非线性梁方程,运用算子分解和带权空间上构造紧算子的方法,得到了该方程在无界区域R1上存在全局吸引子.
非线性梁方程;全局吸引子;算子分解
研究一类非线性梁方程,其形式如下
utt+Δ2u+δut+g(u)=h
(1)
u(x,0)=u1(x),ut(x,0)=u2(x)
(2)
其中u(x,t)描述了桥面在竖直平面内的变形,t∈R+,x∈R1;δ表示黏性阻尼.研究方程(1)这样具有耗散性质的无穷维动力系统解的长时间性态是数学物理中的一个重要问题[1].有关无界区域上的紧吸引子的存在性问题主要困难在于Hs(Rn)嵌入Hs1(Rn)(s>s1)是不紧的,即无界区域上Sobolev嵌入定理不再成立.1990年BabinAV修正了“紧正向不变集”[2]条件,引入带权空间构造紧算子,从而解决了无界区域上全局吸引子的存在性问题.文[3]研究了方程(1)在有界区域上的全局吸引子的存在性,但方程(1)在无界区域上的全局吸引子的存在性尚无结果.本文采用文献[4]和[5]中的算子分解技巧,解决了Hs(R1)嵌入Hs1(R1)(s>s1)不紧的问题,并且利用Kuratowskiα-非紧测度证明了解算子S(t)的渐近光滑性,最后由HaleJK[5]的定理得到无界区域R1上的非线性梁方程(1)-(2)全局吸引子的存在性.
1 解算子S(t)的存在性
E0=H2×L2(R1);E1=H3×H1(R1);E2=H4×H2(R1)
用‖·‖Ei(i=0,1,2)分别表示Ei中的范数.文中后面将会多次用到下面的Gagliardo-Nirenberg不等式
(3)
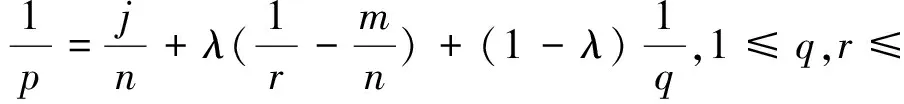
假设非线性函数g满足下面的条件:
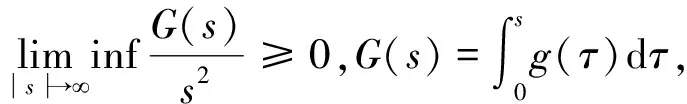
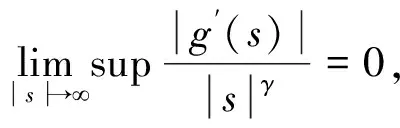
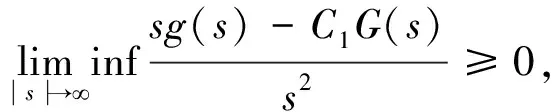
设任意有界集B0⊂E0,根据Poincare不等式,存在常数λ1使得
‖Δu‖≥λ1‖u‖
(4)
引理1 设δ>0,h(x)∈L(R+;L2(R1)),g(u)满足条件(H1)-(H3),∀(u1,u2)∈E0,则(u,ut)∈L(R+;E0(R1))且存在t1(R)>0,∀t≥t1(R),‖(u1,u2)‖E0≤R,有‖(u,ut)‖E0≤C.
证明 由条件(H1)、(H3),对任意u∈H2(R1),存在仅依赖于u的常数K1、K2,使得
(5)
(6)
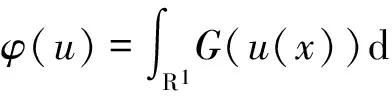
(7)
用ν=ut+εu与(1)在L2中作内积得:
(8)
根据(4)、(7)及Hölder不等式和Young′s不等式得
(9)
(10)
利用(6)式可得
(11)
结合(9)、(10)和(11),由(8)可得
(12)
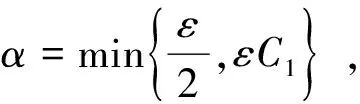
(13)
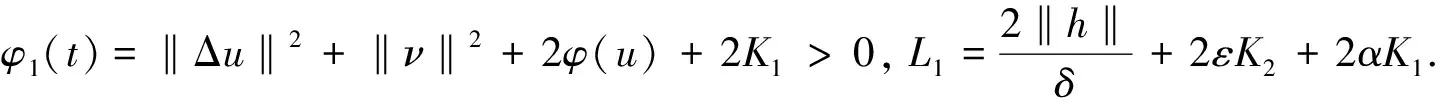
则由Gronwall引理可得
(14)
再利用Gagliardo-Nirenberg不等式‖u‖2≤C‖u‖‖Δu‖,则引理1得证.
引理2 设δ>0,h(x)∈L(R+;H1(R1)),g(u)满足条件(H1)-(H3),∀(u1,u2)∈E1,则(u,ut)∈L(R+;E1(R1))且存在t2(R)>t1(R),∀t≥t2(R), ‖(u1,u2)‖E1≤R,有‖(u,ut)‖E1≤C.
证明 用-Δν=-Δut+εΔu与(1)在L2中作内积,并用引理1可得
+(δ-ε)‖ν‖2+ε3‖u‖2+(g(u),-Δν)≤(h,-Δν)+εδμ2
(15)
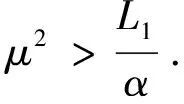
由条件(H2)、Young′s不等式和引理1,存在常数K3>0,使得‖g′(u)‖≤K3,则
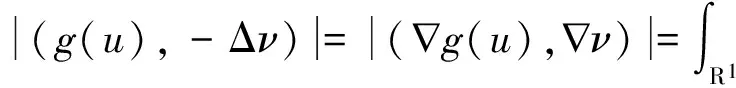
≤K3‖u‖‖ν‖≤ε‖ν‖2+C2
(16)
C2是依赖于K3、μ2、ε的常数.同样有:
(h,-Δν)≤ε‖ν‖2+C3
(17)
C3是依赖于‖h′‖、μ2、ε的常数.

+2ε3‖u‖2≤4L2+2εδμ2
(18)
记φ2(t)=‖Δu‖2+‖ν‖2+ε2‖u‖2.则对充分小的ε,有
(19)
由(3)式和Gronwall引理可得引理2.
引理3 设δ>0,h(x)∈L(R+;H2(R1)),g(u)满足条件(H1)-(H3),∀(u1,u2)∈E2,则(u,ut)∈L(R+;E2(R1))且存在t3(R)>t2(R),∀t≥t3(R),‖(u1,u2)‖E2≤R,有‖(u,ut)‖E2≤C
证明 用与引理1和引理2相同的方法可证该引理.
推论1 设h(x)∈L(R+;H2(R1)),∀(u1,u2)∈E2,有(u,ut)∈L(R+×R1).
定理1δ>0,h(x)∈L(R+;H1(R1)),g(u)满足条件(H1)-(H3),对任意(u1,u2)∈E1,方程(1)-(2)存在唯一解(u,ut)∈L(R+;E1(R1))且解算子S(t)是E1到E1连续的并有有界吸收集B1⊂E1(R1).
证明 由文献[6]中标准的Faedo-Galerkin方法易证解的局部存在,然后利用引理1和引理2的估计得解的整体性,唯一性可由S(t)在E1的连续性得到.
定理2δ>0,h(x)∈L(R+;H2(R1)),g(u)满足条件(H1)-(H3),对任意(u1,u2)∈E2,方程(1)-(2)存在唯一解(u,ut)∈L(R+;E2(R1))并有S(t)是E2到E2连续的且存在有界吸收集B2⊂E2(R1).
该定理的证明与定理1类似.
2 算子分解
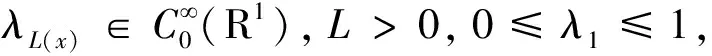
当L→+时,由于h(x)∈H2(R1),则序列hλL在H2(R1)上趋于h(x).对任意的ξ∈(0,1),有L(ξ)>0,使得
(20)
(21)
下面分解方程(1)-(2)对应的解算子S(t)=S1ξ(t)+S2ξ(t),其中S1ξ(t)满足S1ξ(t)(u1,u2)=(uξ,uξt)是如下方程的解:
uξtt+Δ2uξ+δuξt-ξΔuξ+g(uξ)=h-hξ-ξΔu
(22)
uξ(x,0)=u1(x),uξt(x,0)=u2(x)
(23)
记(wξ,wξt)=S2ξ(t)(u1,u2)是如下方程的解:
wξtt+Δ2wξ+δwξt-ξΔwξ+g(wξ)=hξ
(24)
(25)
引理4 在引理3的条件下,存在常数C>0,使得
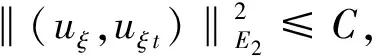

证明 用νξ=uξt+εuξ与(22)在L2中作内积,由引理1的估计可得
+δ‖νξ‖2+2ξε‖uξ‖2+2εC1φ(u)+2εC1K1
≤‖h-hξ‖‖νξ‖+ξ‖Δuξ(1-λL(ξ))‖‖νξ‖+2εK2+2εC1K1
(26)
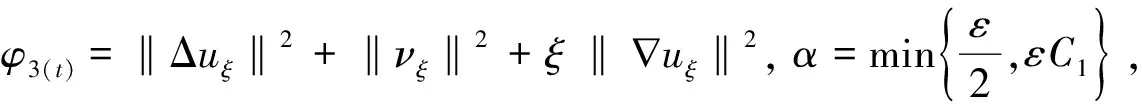
(27)
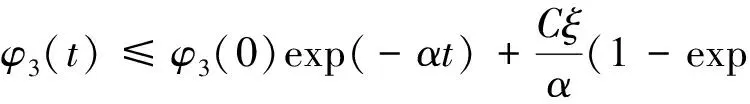
‖Δuξ‖2+‖uξ‖2+‖uξ‖2+‖uξt‖2≤C,∀ξ∈(0,1),∀t≥0
(28)
存在t1(ξ)>0,使得
‖Δuξ‖2+‖uξ‖2+‖uξ‖2+‖uξt‖2≤Cξ,∀ξ∈(0,1),∀t≥t1(ξ)
(29)
下面用-Δνξ=-Δuξt-εΔuξ和Δ2νξ=Δ2uξt+εΔ2uξ分别与(22)作内积,作与上面类似的讨论有
‖Δuξ‖2、‖Δ2uξ‖2、‖uξt‖2、‖Δuξt‖2≤C,∀ξ∈(0,1),∀t≥0
且存在t4(R)≥t3(R),使得
‖Δuξ‖2、‖Δ2uξ‖2、‖uξt‖2、‖Δuξt‖2≤Cξ,∀ξ∈(0,1),∀t≥t4(R)
引理证毕.
引理5 在引理3的条件下,存在一常数C(ξ)>0,使得
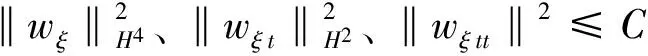
证明 由于u和ut在H4(R1)和H2(R1)中有界,uξ和uξt也在H4(R1)和H2(R1)中有界,则wξ=u-uξ在H4(R1)中有界且wξt=ut-uξt在H2(R1)中有界,因此由(24)得(wξtt,wξtt)=(ξΔwξ+hξ-Δ2wξ-δwξt-g(wξ),wξtt),则
‖wξtt‖2≤‖wξtt‖(‖ξΔwξ‖+‖hξ‖+‖Δ2wξ‖+‖δwξt‖+‖g(wξ)‖)
引理证毕.
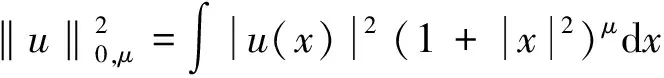

(30)
(31)
并且有估计式
(32)
引理6 在引理2的条件下,存在常数C(ξ)>0,使得
(ξ),∀ξ∈(0,1)
证明 用ψη=ψwξt+εψwξ与(24)作内积得
(33)
其中
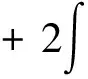
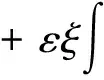
下面对各项作估计
再用相同的方法估计下面几项
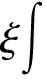
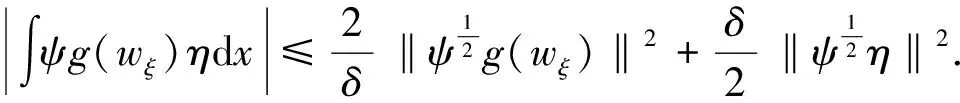
再用-ψΔη=-ψΔwξt-εψΔwξ与(24)作内积,同上可得
引理证毕.
3 全局吸引子的存在性
引理7[3,7]设s>s1,s、s1为整数,则Hs(Rn)∩Hs1(Rn;(1+x2)dx)到Hs1(Rn)紧嵌入.
定理3δ>0,h(x)∈L(R+;H2(R1)),g(u)满足条件(H1)-(H3),由(1)-(2)所生成的解半群S(t)在E1中有全局吸引子它按E1的拓扑吸引E2中的任意有界集.
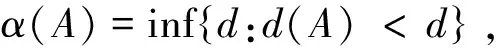
α(S(t)B)≤α(S1ξ(t)B)+α(S2ξ(t)B)=α(S1ξ(t)B)≤ε,∀t≥0
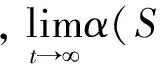
[1] 金俊林,王万雄.非线性可拉伸梁方程非自洽指数吸引子的存在性[J].云南民族大学学报:自然科学版,2013,22(5):341-345.
[2]BABINAV,VISKIKMI.Attractorsofevolutionequations[M].NewYork:ElsevierSciencePublishingCompany,1992.
[3] 马巧珍,孙春友,钟承奎.非线性梁方程强全局吸引子的存在性[J].数学物理学报:A辑,2007,27(5):941-948.
[4]GUOBOLING,LIYONGSHENG.AttractorfordissipativeKlein-Gordon-SchrodingerequationsinR3[J].J.Diff.Eq.,1997,136(2):356-377.
[5]LIYONGSHENG,GUOBOLING.AttractorfordissipativeZakharovequationsinanunboundeddomain[J].ReviewsinMathPhysics,1997,9(6):675-687.
[6]TEMAMR.Infinitedimensiondynamicalsystemsinmechanicsandphysics[M].NewYork:Springer-Verlag,1988.
[7]HALEJK.Asymptoticbehaviorofdissipativesystems[M].NewYork:AmericanMathematicalSociety,1988.
[8]BABINAV,VISKIKMI.Attractorsofparticaldifferentialevolutionequationinanunboundeddomain[J].Proc.Roy.Soc.Edinburgh,1990,116(A):221-243.
Global Attractor of the Nonlinear Beam Equations on Unbounded DomainR1
JIANG Jin-ping, ZHANG Xiao-ming
(College of Mathematics and Computer Science,Yan′an University,Yan′an 716000,China)
The nonlinear beam equations represent the vibration of the rode bed in downward direction.The nonlinear beam equations is investigated on unbounded domain R1.Byapplyingthemethodofdecomposingoperatorandconstructingcompactoperatorinweightedspace,theexistenceofglobalattractorisobtainedinR1.
Nonlinear beam equation;Global attractor;Decomposition of operator
2015-05-19
陕西省科技计划资助项目(2014K15-03-07);陕西省教育厅科研基金资助项目(14JK1841);延安市科技计划资助项目(2013-KS03).
姜金平(1974-),男,陕西洛川人,博士,副教授,硕士生导师,主要从事无穷维动力系统方面研究.E-mail:yadxjjp@163.com.
姜金平.
O
A
1007-9793(2015)04-0034-07
