导数在高中数学函数中的应用体会探索
2015-04-30黄书龙
黄书龙
【摘 要】导数属于一个比较特殊的函数,同时,导数的引出以及相关的定义都涵盖了函数的基本思想,新课程的改革中,也对导数的具体知识内容进行了相应的深化,同时切线、不等式以及数列等都带来了新的解决思路,对众多数学理论知识提供了更加便捷的解决方法。本文重点研究的是导数在高中数学函数教学中的具体应用,分别从函数图像的具体作法,函数具体单调性进行讨论以及函数具体的最值求解方法等三个方面进行分析。
【关键词】导数;高中数学;函数;应用;体会与探究
随着我国对高中课程的不断改革,高中数学的相关教学也逐渐从理论知识教学转化成实用性知识教学。导数的相关理论知识在研究曲线具体的切线以及解决实际问题中具有非常广泛的应用,于此同时,导数对于研究函数具体的单调区间,以及函数相应的最值问题,证明不等式,对方程进行求解,数列的求和等各个数学方面的知识都提供了非常便捷的解决方法,因此,导数的学习在高中数学的学习中占有非常重要的位置。利用导数的相关理论知识能够深入研究物理运动的具体变化,在如今现代化建设的众多领域中都具有非常广泛的应用。导数对高中数学的学习也具有非常重要的引导作用。本文主要研究的是导数在高中数学函数学习中的具体应用。
一、函数图像的具体作法
在高中数学的教材中,利用描点的方法作出各种函数图像,但是作图的过程以及效果都比较粗糙,并且并不十分准确,一般情况下,这种描点的方式只适用于一些非常简单的函数图像,对于一些非常复杂的函数,利用描点的方式很难做出相应的图像。现在利用导数的相应理论知识能够非常容易地做出比较准确的函数图像,同时方法比较方便简单。利用导数的相关内容分析整个函数具有的基本性质,判断函数呈现的单调性,最后求出函数的最值等内容,得出比较准确的函数图像。
例1:做函数图像y = x3+6x2?15x?20.
解:
得出函数具体的定义域为(?∞,+∞)。
(2)其中曲线与x以及y轴之前的交点为,(-1,0),(0,-20)。
(3)设y′=3x2+12x?15=0,最后解得数值x=?5或者x=1。
设y′′=6x+12=0,最后解得数值x=?2。
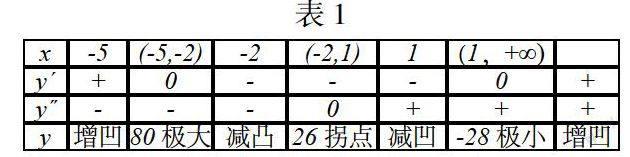
(4)通过列表的方式讨论函数具有的单调区间,函数的极值点,函数的凸性区间以及函数的拐点,如表1。
(5)不存在渐进线。
(6)根据具体数值做出最终的图像。
二、函数具体单调性进行讨论
函数具有单调性是所有函数自身具有的最基本的性质,也是对函数进行研究需要了解的基本的数学理论知识。单调性具体的定义对于处理各种单调性相关的问题具有非常强的技巧性,并且掌握起来并不容易,利用导数的相关知识内容判断函数具有的单调性,非常简短便捷,并且容易掌握,理解起来比较容易。
例2:函数f(x)=x3-3x,确定这一函数具体在哪一个区间呈现的是增函数,在哪一个区间呈现的是减函数。
分析:对上述函数进行求导,并且,求不等式f′( x)<0以及f′(x)>0具体的解,其中,f′(x)<0具体的解就是整个函数的单调区间。
解:由于函数具体的导数函数为f′(x)=3(x+1)(x-1),设f(x)′>0,最终可以得出x<1或者是x>1,因此上述函数具体的单调增区间是(?∞,?1)以及(1,+∞)。
函数具体的最值的求解方法
函数最值的相关问题也属于高中数学学习中的一个非常重要的知识内容,也属于高中数学的重点难点,函数的最值问题涉及到高中数学中各个方面的理论知识,涉及的面非常广泛,利用导数解决函数的最值问题,能够有效地简化整个解题的过程,并且整个过程也非常广泛,步骤比较清晰明确,方便学生理解,并能更加清楚地掌握相应的知识内容。
一般情况下,函数的闭区间在[a,b]属于可导区间,那么,函数在[a,b]这一区间具体的最值求法为,首先,需要求出函数在(a,b)上具体的驻点,其次,计算出函数在驻点以及端点内具体的函数值,通过比较可以得出,其中最大的一个数值及时最大值,其中最下的一个数值就是最小值。实际上,这一解决的方案可以利用本文中的第一个性质进行解答,也就是利用作图的方式解答。因此,在进行作图的整个过程中,需要求出具体的极值点以及函数的最值点,因此,利用作图的方式或者是利用求最值的方法都存在一些非常相似的步骤以及相同的数学思维方法。
例3:函数f(x)=x3-x2/2-2x+c2,如果,x∈[?1,2],那么f(x) 分析:面对这样的数学题目,想要找出解题的方法最重要就是要深刻地理解函数的相关理论知识,并学会灵活的运用,上题中,问题的实质就是确定函数y=g(x)具体的最大值是多少。 解:设g(x)=x3-x2/2-2x,因此任意的x都有x∈[?1,2],并且g(x)?c2-c恒成立,其中g′(x)=(x?1)(3x+2),如果x发生一定的变那么g(x)以及g′(x)也会同时发生变化,由于g(2)=2,因此,对于任意的x,并且x∈[?1,2],函数最大值为g(2)=2。最终得出,c∈(?∞,?1)∪(2,+∞)。 三、结束语 综上所述,导数是解决数学众多问题的一个关键工具,利用导数的数学思想对解决众多数学问题都具有非常重要的意义,也提供了一些非常方便简单的解题方法。尤其是利用导数的相关知识内容解决函数具有单调性、极值以及最值等数學问题中,非常方便并且容易掌握。在利用导数解决各种数学问题的整个过程中,能够引入非常优化的数学思维方法,整个解题过程也非常简单便捷,掌握了数学导数的相关知识内容,为高中学生提供了一种更加方便的数学解题工具,帮助学生深入地理解函数的基本概念,并通过导数直观地认识与理解函数的相关理论知识内容。 参考文献: [1]丁伟.中学数学教学参考[J].陕西师范大学中学教学参考杂志社出版,2010 [2]毕明黎,王丽.中学数学研究[J].华南师范大学数学科学学院,2011,(3) [3]高慧明.中学数学研究[J].华南师范大学数学科学学院,2011,(9)
