让学生担当课堂的主角
2015-04-28内蒙古赤峰市赤峰二中郭桂玲
☉内蒙古赤峰市赤峰二中 郭桂玲
让学生担当课堂的主角
☉内蒙古赤峰市赤峰二中 郭桂玲
新课程倡导教师积极转变教与学的方式,把主动权还给学生,教师应是学生发展的促进者,是学生学习的组织者、引导者、参与者和欣赏者.教师在充分放手让学生思考的基础上,又能准确启发指导.本文以“点到直线的距离”的教学为例说明.
一、教学设计思路
“点到直线的距离”是“坐标平面上的直线”一章的最后一节内容.我们希望找到一种教学方案,既渗透解析法的方程思想,又体会向量方法的便捷性,我们决定将问题交给学生,放手让学生去探究“如何求点到直线间的距离”这个问题.我们希望通过教学,帮助学生学会推导点到直线的距离公式,并掌握点到直线的距离公式;通过对点到直线间距离公式推导方法的分析、比较与体验,引导学生领悟公式推导过程中的数学思想和思维方法,培养学生分析问题和解决问题的能力.在教学过程中,点到直线的距离公式及其推导过程是教学重点;如何引导学生学习和领悟对问题的思维过程及所蕴含的教学思想方法,这应该是教学的难点.
二、教学设计过程
1.引入
通过师生对话问答回顾知识,将知识结构化,形成以下知识结构.
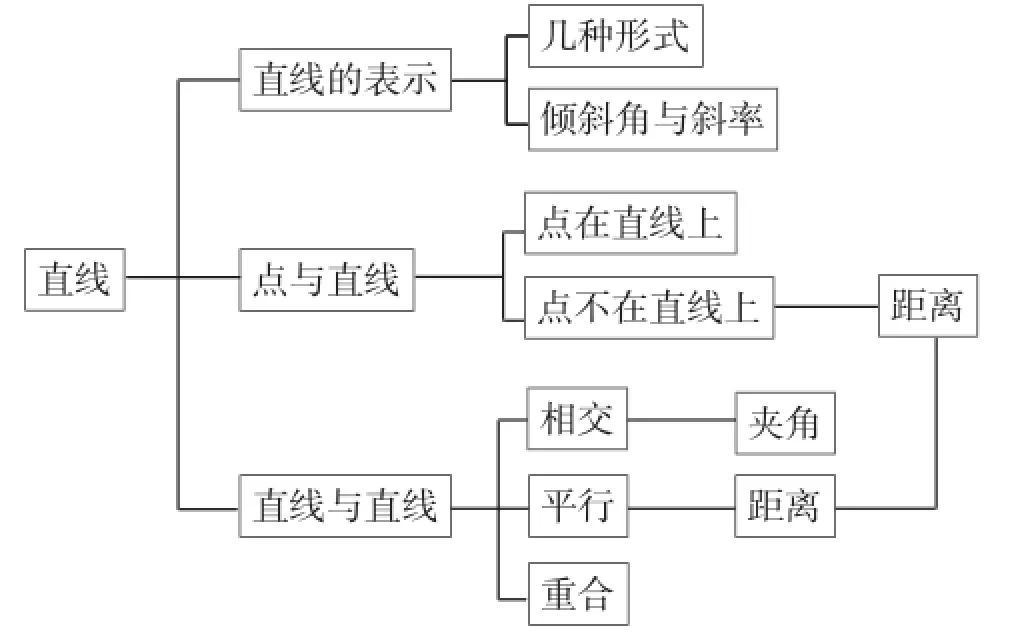
图1
说明:引入中,从学生原有的知识基础出发,通过知识的逻辑结构说明为什么学习点到直线的距离,激发学生学习的兴趣,强调理性思维.
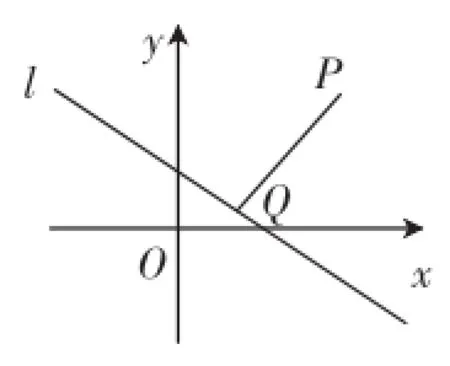
图2
2.点到直线的距离公式的推导
(1)明确并提出问题.
如图2,已知直线l∶Ax+By+C=0,直线外一点P(x0,y0),其中A、B、C、x0、y0为常数,如何表示点P到直线l的距离d?
在解决该问题前可以作如下铺垫.
师:什么是点到直线的距离?P到l的距离是一个确定的值吗?如何求点P(x0,y0)到直线l:Ax+By+C=0的距离?
师:作PQ⊥l于Q,如何计算线段PQ的长度?你能想到哪些方法?(同学们思考讨论)
说明:这里先回顾“什么是点到直线的距离?”从几何角度作出距离|PQ|,并指出点到直线的距离其实是点到直线上任意一点的距离的最小值.再指出点P到直线的距离是一个确定的值,它可以用常数x0、y0、A、B、C表示.最后引导学生思考问题的解决途径,进入讨论.
(2)推导点到直线的距离公式.
通过对问题的初步分析,我们将”求点到直线之间的距离”归结为“如何计算线段PQ的长度?”因为求线段长的方法有许多种,所以可以先由学生充分探索,再通过合理有效的组织,引导学生掌握方法的本源,寻找问题的解决方法.
①充分引导学生自主探索,展现问题解决的思维过程.
生1:计算Q点的坐标.
师:为什么想到求Q点的坐标?如何计算Q点的坐标?生1:有下列两种方法.
(1)解联立方程组,写出直线PQ的方程,联立PQ与l的方程,求解Q点的坐标(x1,y1).
(2)利用数量积计算Q点的坐标,设Q(x1,y1)
师:这种方法是一定可以做到底的,就是不知道解方程会不会给我们带来麻烦.先放一下,其他同学还有其他方法吗?
生2:为避免求Q点的坐标,可用面积相等.(示意想到黑板上作图说明)
生2:利用三角形面积公式可知|PQ|·|RS|=|PR|·|PS|,从而可求|PQ|.
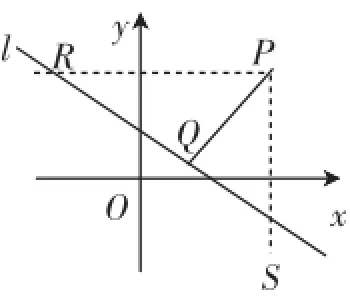
图3
生3:用向量的数量积.
师:为什么会想到数量积?
师:这个方法值得一试,设想一下它后续的一些步骤,可能会遇到什么问题?M点的坐标需要代换,如何代换?注意点M在直线上,能否得出结果,我们待会可以尝试一下.
师:还有其他方法吗?
学生又提出了利用三角比、勾股定理等平面几何知识,利用函数思想求距离的最小值等方法.
②合理选择解题方法,突出方程思想与向量方法.
师:所有这些都可以试一试,现在,我们选择两种典型的、有代表性的,也是有一般意义的方法:(1)用生2的方法解联立方程组,看看能否算出|PQ|的长度;(2)向量方法是一个重要的解决问题的方法,试一试能否用向量的数量积将|PQ|的长度算出来?
(学生分组讨论,派代表到黑板上板演)
生4:由P(x0,y0),可设R(x1,y0),S(x0,y2).又R、S在直

师:这个方法的关键是什么?
生4:利用了方程思想和整体代换思想.
师:好,我们再看用向量方法计算出|PQ|.
师;在这个方法中,你们认为关键是什么?
生:数量积及在直线上的点的坐标满足直线方程.
③回顾反思两种方法,体验其中的数学思想.
师:刚才我们用解析几何中两种典型的方法计算出:点P(x0,y0)到直线l:Ax+By+C=0的距离d.虽然方法有许多种,但是因为解析几何的核心思想是利用方程研究曲线,所以解联立方程组是基本方法,又因为向量在解析几何中是一个重要的知识和方法,计算简洁,体现了向量方法的优势,值得我们细细体会.
三、公式的应用
师:现在你们能推导两条平行线之间的距离公式吗?
问题:若直线l1:Ax+By+C1=0,l2:Ax+By+C2=0,其中A、B、C1、C2为常数,且C1≠C2,如何求l1与l2的距离?
这个问题由学生独立解决,教师主要是引导并介绍方法.
生6:利用点到直线的距离(转化为求点到直线间的距离).
在直线l1上取点P(x0,y0),则
由Ax0+By0+C1=0,得Ax0+By0=-C1,所
师:还有没有其他方法?
生7:也可以用向量的数量积(直接利用向量方法求距离).
师:这个式子可作为公式使用,但要注意A、B的一致性.
在新课标的要求下,我们要充分发挥学生的主观能动性,在突出学生自主学习的基础上,教师作适当引导.教师要善于捕捉来自于学生的智慧和火花,敢于采纳学生的点子和方案,这样有利于充分调动学生的积极性、主动性,有利于增强学生的自信心.给学生一个宽广的舞台吧,让学生担当课堂的主角,让他们的思维激情燃烧.
1.普通高中数学课程标准(实验)解读[M].南京:江苏教育出版社,2004.
2.方国才.新课程怎样教得精彩[M].北京:中国科学技术出版社,2006.A
