数学教学要重视知识的形成过程——以“极坐标”教学为例

☉广东省广州市真光中学 金明 叶东芳

数学教学要重视知识的形成过程
——以“极坐标”教学为例

☉广东省广州市真光中学 金明 叶东芳

一、问题提出

在中学数学教学中，由于受高考的影响，部分教师的教学还存在“急功近利”的思想，即高考考什么，我就教什么；不考的，就不教.在教学过程中，强调知识的应用，不重视它的形成与发展过程.学生学到的只是定理、公式等的应用，认为数学只是做题解题，体会不到学习数学的乐趣.如广东高考每年必考一道极坐标与参数方程的选做题，而此题主要考查极坐标的概念，直角坐标与极坐标的互化，为此一些老师上课时直入主题，只讲什么是极坐标系，极坐标与直角坐标的互化，然后通过大量的练习来巩固这两个知识点.至于为什么要构建极坐标系，怎样构建极坐标系，为什么要进行极坐标与直角坐标的互化等都不提，只重视套公式做题，不重视知识的形成过程、知识的发生和发展过程.长此下去，学生的学习缺乏后劲，不知数学知识的来源与发展；学生的学习兴趣不能持续，学习缺乏动力.为此，笔者以“极坐标”教学为例，设计了一堂重视知识形成过程的课例.

二、教学实录

1.创设问题情境，导出建立极坐标系的必要性

师：在现实生活中，经常出现要指明一个点的位置，如图1（ppt展示），有人在教学楼A处问你怎样找到图书馆C，请你给他指引路线.如何设计？

师：为什么要这样设计？依据是什么？

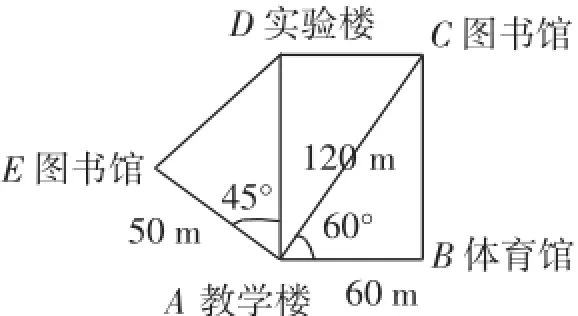
图1

生1：如图2，以A为坐标原点，AB为x轴，建立直角坐标系，则C点的坐标为（60，

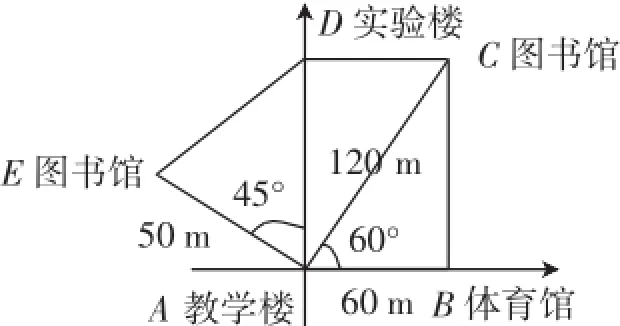
图2

生2：以A为起点，向东偏北60°的方向一直走120 m.

师：你的设计依据是什么呢？

生2：C在A的东偏北60°且距离A120 m处.

师：由生2的回答知：刻画一个点的位置，除了直角坐标系，还有新的方法，这个方法需要什么呢？

生3：需要方向和长度.

教学感悟：教学一开始，由一个具体的实际问题导出，指明刻画一个点的位置除了已学过的直角坐标，还有新的方法.新方法到底是什么呢？它的理论依据又如何？为极坐标系的建立作了铺垫.同时，激起了学生探索新知识的兴趣.

2.建构知识：如何建立极坐标系

师：能具体化吗？需要什么方向？怎样的长度？

生3：方向是东偏北60°，长度是距离A120 m.

师：一定要东偏北的方向吗？一定要到A的距离吗？

生4：方向也可以是东偏北30°，距离A120 m；一定要到A的距离.

师：物理学中我们学过参照系，刻画C点的位置是否也要参照什么东西？

生5：以A点为参照点就行.

师：真的吗？以A点为参照点怎样刻画C点的位置？

生5：距离A点120 m，哦，不对，还要有方向.

生6：以A点和直线AB作参照，能刻画C点的位置：AB逆时针旋转60°且距离A120 m就行.

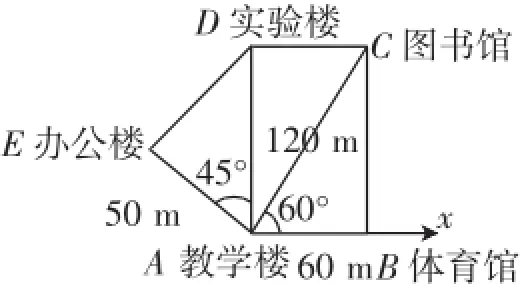
图4

图3

师：生6说的很好，刻画一个点的位置，由一个点和一条直线作参照就可行，为此我们引进一个新的坐标系——极坐标系.如图3，在平面内取一定点O，叫做极点，引一条射线Ox，叫做极轴，再选定一个长度单位和角度（通常是弧度制）及它的方向（通常取逆时针方向）.对于平面上任意一点M，用ρ表示线段OM的长度，ρ叫做点M的极径，用θ表示Ox到OM的角度，θ叫做点M的极角，则有序数对（ρ，θ）就叫做M的极坐标.根据刚才的定义，图1中如何建立极坐标系？各点的极坐标是什么呢？

师：对吗？生众：对.师：特别说明，A点为极点，其极径ρ=0，极角θ可以取任意角.

教学感悟：极坐标系是如何建立的？教师通过不断追问如何通过新方法刻画一个点的位置，为极坐标系的建立奠定了基础.引导学生类比物理学中的参照系，使学生体会到建立极坐标系要有极点与极轴.再讲解极坐标系中的有关概念：极点、极轴、极径、极角.这样学生就体会到知识的形成是自然的，不是教师强加的；学生就易于理解极坐标的有关概念了，对新知识的构建也找到理论依据了，激起了学生探索新知识的乐趣.

3.极坐标系的应用

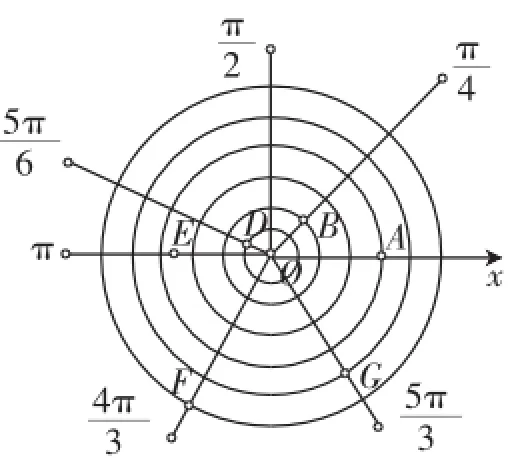
图5

生众：这几个点分别是：E、G、F、F.

问题2：写出图5中各点的极坐标：A（），B（），C（），D（），E（）.

生9：有没有别的表示方法？

（引起了大家的思考）

生8：没有吧，极坐标系已建立，是按逆时针方向.生9：好像还有，你看问题1中的两个F点.

师：生9能联系上下题发现问题，提出问题，很好.我们一起来讨论下面的几个问题：

①平面上一点的极坐标是否唯一？

②若不唯一，它的极坐标有多少种表示方法？

③坐标不唯一是由谁引起的？不同的极坐标是否可以写出统一表达式？

④提出怎样的假设，能使一个点的极坐标表示唯一呢？

（学生分小组讨论，小组长总结）

小组1：平面上一点的极坐标不唯一.因为旋转方向不一致，旋转角的大小不一样.

小组2：同意小组1的结论，旋转角可相差2kπ，一个点的极坐标有无数种表示方法.

小组3：坐标不唯一是由旋转方向不一致和旋转角的大小不一样引起的.不同的极坐标可以写出统一表达式（ρ，θ+2kπ），k∈Z.

小组4：只要旋转方向规定为逆时针方向，旋转角规定为（0，2π），则能使一个点的极坐标表示唯一.

师：很好，同学们的讨论很成功，以上4个小组的总结结论都是正确的.今后没特别说明，就按旋转方向规定为逆时针方向，旋转角规定为（0，2π）.

图6

师：生10做得很好，她能建立极坐标系，找出A、B的位置，再分析解答，建系找位置是我们刚学极坐标系的难点.

教学感悟：教师通过精心设计问题，引起学生思考，在解决问题的过程中，学生学会了探索与质疑.问题1和问题2的解答为生9的质疑作了铺垫.教师根据生9的质疑设计了4个问题让学生分组讨论，教师到各小组指导，最后小组代表作总结发言.学生做到了自主探索，合作交流，课堂教学充分地发挥了学生的主观能动性.教师所设计的讨论题是学生易误解的，又是能通过讨论解决的.通过讨论激起了学生的思维碰撞，激发了学生的学习动力.学生在探索中体验到数学学习的乐趣.

4.极坐标与直角坐标互化的必要性

师：我们再来思考一下问题4.

生11：我先建系，找出点M、N，如图7，下面就不知道怎么做了.

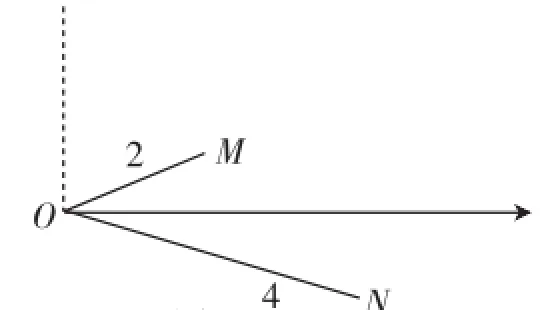
图7

师：有人能帮帮生11吗？

（生众沉默）

师：在极坐标系下求圆的方程没有学过，故同学们不会求情有可原.如果知道M、N两点的直角坐标，能求圆的方程吗？

生众：简单，只求圆心与半径就行.

师：我们能否将极坐标转化为直角坐标呢？怎样转化呢？

教学感悟：问题4的设计引出了极坐标与直角坐标互化的必要性，使学生进一步体验到：知识不是教师强加给学生的，而是客观实际的需求，激发了学生的学习兴趣，为探讨新知识做了铺垫.

5.极坐标与直角坐标怎样互化

生12：互化要有前提条件吧！

师：很好，互化确实需要前提条件：第一是坐标系的建立要一致，第二是要取相同的单位长度.如图8，以极点为坐标原点，极轴为x轴的正半轴，取相同的单位长度，建立直角坐标系.则M点的极坐标为（ρ，θ），M点的直角坐标为（x，y）.能建立它们的联系吗？

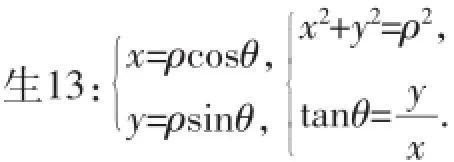
图8

师：对吗？其理论依据是什么？生14：对，理论依据是直角三角形中的三角函数.师：如图9，若点M在第二象限内，还适用吗？

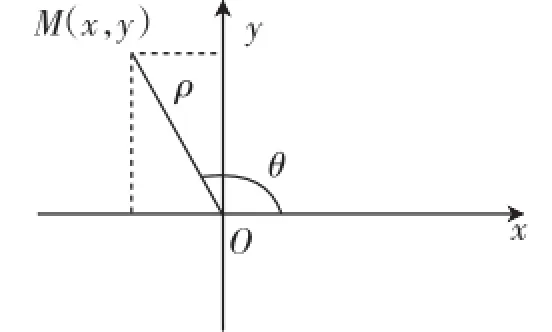
图9

生15：还适用，理论依据是三角函数的定义对任何象限都适用.

师：生15的回答很好，理论依据是三角函数的定义.

教学感悟：为什么能将极坐标转化为直角坐标？教师先设计一个学生解答起来有点困难的问题，引发学生思考，说明将极坐标转化为直角坐标的必要性.怎样转化呢？转化的理论依据是什么？教师通过不断追问找到其中的原因，构建了新、旧知识的联系，培养了学生寻根问底的习惯，使之逐渐形成良好的数学素养.

师：请同学们思考问题5.

师：对吗？

师：由此可见，不能盲目地套用公式，要想准确，先要画图确定位置.同学们思考一下刚才的问题4，能解答吗？

师：生19将极坐标转化为直角坐标，求出了圆的方程.但是以这个方程作为问题4的答案还是有点问题，因为题目中给出的是极坐标系，故所求方程还要化为极坐标系下的方程.

教学感悟：通过一组解题训练，巩固了知识：极坐标与直角坐标如何互化，体验了知识的应用，构建了知识体系.

三、教学反思

1.偏重数学结论而忽视数学过程，是数学教学过程中长期存在的问题

从学生方面来讲，同学间的相互交流仅是对答案，交流各自的解法，很少见到同学间有对数学问题的深层次讨论和对解题方法的创造性研究.至于思维变式、问题变式更难有涉及.从教师方面来讲，也存在自觉不自觉地忽视数学问题的解决过程，忽视结论的形成过程，忽视解题方法的探索过程，对学生的评价一般也只看“结论”评分，很少顾及“数学过程”.应试教育的弊端之一在于缩短了新授课中知识形成过程的教学，使学生很难实现数学的有意义学习，只是对数学的基本概念如定义、公式法则的机械记忆.而机械记忆的知识是很难产生广泛的迁移的，缺乏迁移的知识是无法转变成能力的.知识形成过程的新授课教学，应是培养一般思维和数学特殊思维方法的重要时机.因为在新知识学习过程中，必须运用各种思维方法在新旧知识间进行相互作用，才能建立起新、旧知识间非人为的实质性联系，如果压缩知识形成过程，其被压缩的往往是学生既可学习思维方法，又可领会数学思想和方法的过程.学生将错过或失去思维发展和能力提高的机遇.

2.数学教学要重视知识的形成过程

数学是一门基础学科，其知识的系统性使知识间的内在联系十分紧密.任何新知识或者因为某种需要而产生，或者因为某种需要，要将原有知识进行延伸和发展.所以任何新知识都有它的发生、形成和发展过程.教学中，如果压缩掉这种过程，就知识教知识，那么学生只能得到零散的、孤立的知识；只知其然，而不知其所以然；只能是知识的简单积累，而不能使学生原有的知识得到扩充和改造.课堂上让学生感受数学的作用，体验到数学的概念、定理中所蕴含的独特的理性精神与思想方法；激发学生对数学的爱好和兴趣，体验到学习数学的无限乐趣，培养学生解决问题的能力.这些知识如果只是靠老师的讲解恐怕是不可能实现的，需要的就是注重过程的有效教学和学生的有效参与.本节课的教学设计，学生知识的获得是自然的，是注重过程的.如为什么要建立极坐标系？是因为实际需要（要刻画一个点的位置）；怎样建立极坐标系呢？是类比物理学中的参照系和直角坐标系建立的；为什么要进行直角坐标与极坐标的互化等都是自然形成的.

3.揭示知识的形成，让知识返璞归真

《高中数学课程标准》指出：数学课程要讲逻辑推理，更要讲道理，通过典例的分析和学生的自主探索活动，使学生理解数学概念、结论的逐步形成过程，体会蕴含在其中的思想方法，追寻数学发展的历史足迹，把数学的学术形态转化为学生易于接受的教育形态.教材的学术形态给教师留下了广阔的空间.教师通过对教材的精心创作，在课堂上还原“脚手架”，让学生看清楼房是怎样建构起来的，让知识的形成返璞归真，让学生像数学家一样经历数学知识的发现过程.本节课在教师的引领下，学生产生了建立极坐标系的必要性，领悟了如何建立极坐标系，体会到在极坐标系下如何确定点的极坐标.在老师设计的问题的引导下，学生产生了极坐标与直角坐标转化的化必要性；通过教师的追问，学生探索出极坐标与直角坐标转化的方法.

1.钱卫江.问题引领：追求自然生成的概念教学——以函数的单调性的教学为例［J］.中学数学（上），2015（2）.

2.张松年.把学习过程中的思维空间让给学生［J］.中学数学教学参考（上），2009（10）.

3.白云峰.慢下来，课堂或许更精彩［J］.中学数学杂志，2012（5）.

4.宫前长.新课程古典概型教学：困惑、解惑与感悟［J］.中学数学（上），2014（5）.A