对一道试题的商榷及命题建议
2015-04-28南通大学附属中学尤荣勇
☉南通大学附属中学 尤荣勇
对一道试题的商榷及命题建议
☉南通大学附属中学 尤荣勇
一、试题再现
上学期我校高二年级期末试卷是请兄弟学校的老师命的题,其中第15题(解答题第1题,共计6个解答题)是这样的:
题目已知p:1<2x<8,q:不等式x2-mx+4≥0恒成立,若﹁p是﹁q的必要条件,求实数m的取值范围.
参考解答:由1<2x<8,得0<x<3,即p:0<x<3.

二、教者争议
我们高二数学备课组老师在做该试题时,大家意见却出现了分歧.部分老师有如下答案:
解法1:与参考答案类似.
解法2:p:0<x<3,﹁p是﹁q的必要条件,即p是q的充分条件,则x2-mx+4≥0对任意x∈(0,3)恒成立.令f(x)=x2-

综上(1)、(2)、(3)所述,m∈(-∞,4].
解法3:设集合A={x|x∈p},集合B={x|x∈q},由条件﹁p是﹁q的必要条件,则A⊆B.显然:A=(0,3).
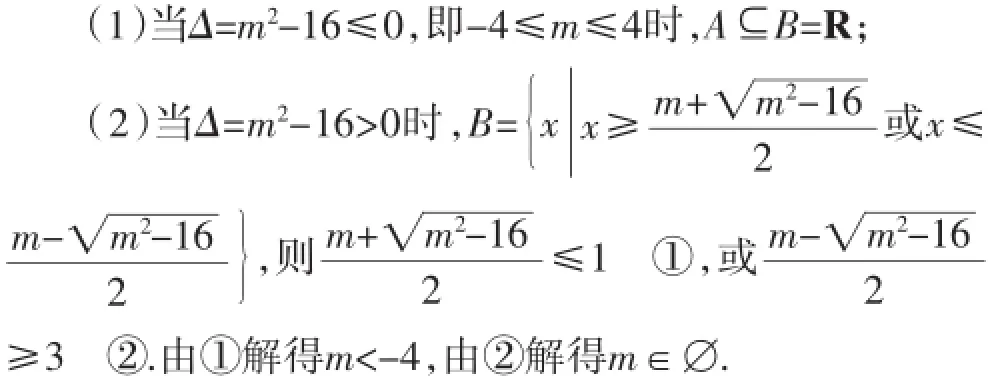
综上所述:m∈(-∞,4].
我们组也有部分老师对该题有不同意见,不妨把上述解法称为正方的解法,那么下面截然不同的意见则是反方的意见:语句q应该是一个独立的命题,不等式x2-mx+4≥0恒成立,那么该不等式是关于变量x还是变量m的不等式呢?不得而知!若不等式是关于m的不等式,设g(m)=-xm+x2+4,则依题意x=0,因为语句p:0<x<3,显然p不是q的充分条件,﹁p不是﹁q的必要条件.显然该不等式只能是关于x的不等式恒成立,此时Δ= m2-16≤0,即-4≤m≤4时,x∈R,此时p:0<x<3是q:x∈R的充分条件,即﹁p是﹁q的必要条件.综上m的范围为-4≤m≤4.
正反双方各执一词,各自认为自己的意见是对的,争议的焦点是:正方认为,语句p是语句q的充分条件,当然q中的不等式是关于x的不等式,且在p成立的条件下恒成立,而反方认为,语句q中没有说明是关于哪个变量的不等式,即便是关于x的不等式,我们说不等式x2-mx+ 4≥0恒成立,一般就是x2-mx+4≥0对一切x∈R均成立的意思,显然这样正方的答案有失科学性.但评卷时,还是尊重参考答案,按照正方的标准评分.我们不妨再来看看学生的答题情况.
三、学生解答及问卷调查
本小题满分14分,我校理科8个班共有308人,年级理科均分5.77分,笔者随机抽样了30份试卷.将其答案、得分大致分类如下表:
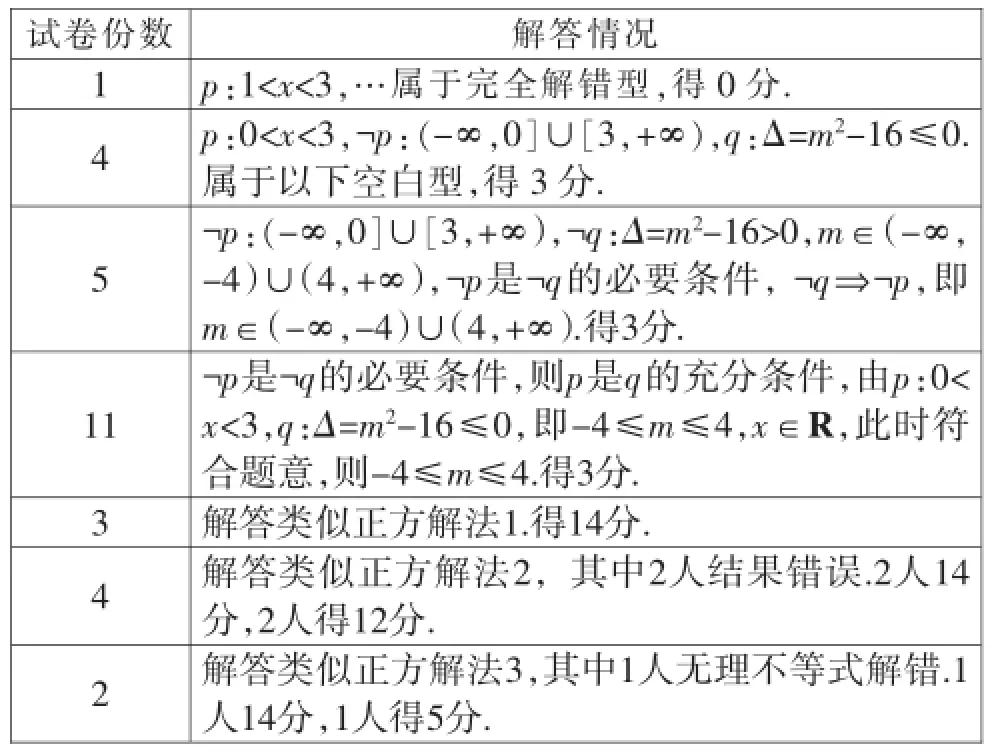
试卷份数解答情况1 p:1<x<3,…属于完全解错型,得0分. 4 p:0<x<3,﹁p:(-∞,0]∪[3,+∞),q:Δ=m2-16≤0.属于以下空白型,得3分. 5﹁p:(-∞,0]∪[3,+∞),﹁q:Δ=m2-16>0,m∈(-∞,-4)∪(4,+∞),﹁p是﹁q的必要条件,﹁q⇒﹁p,即m∈(-∞,-4)∪(4,+∞).得3分. 11﹁p是﹁q的必要条件,则p是q的充分条件,由p:0<x<3,q:Δ=m2-16≤0,即-4≤m≤4,x∈R,此时符合题意,则-4≤m≤4.得3分. 3解答类似正方解法1.得14分. 4解答类似正方解法2,其中2人结果错误.2人14分,2人得12分. 2解答类似正方解法3,其中1人无理不等式解错.1人14分,1人得5分.
针对本题学生的解答、得分情况,笔者对抽样试卷对应的30名同学又进行了一次问卷调查:

问卷调查中的问题多次阅读,还有读不懂题意的感觉你认为本题为容易题已将﹁p是﹁q的必要条件转化为p是q的充分条件或转化为语句p构成的集合是语句q构成集合的子集你看过参考答案后,你对本题题目仍然有异议由于本题解答没把握,较大影响了你后续解答题的求解人数占调查总人数的比例28 93.3% 2 6.6% 24 80% 10 33.3% 23 76.6%
四、对该试题的几点商榷
该试题学生反映读不懂题意,即便是老师,解答本题也颇有争议,那么本题是否存在科学性问题呢?笔者认为,试题表述确有值得商榷之处.
商榷1:语句p中的x就是语句q中的x吗?正方的解答都是默认了语句p中的x就是语句q中的x,这个值得我们推敲.例如A={y|y=x2-1},B={x|x>0},能说集合A,B中的x是同一个x吗?显然不能.如果语句q中的x未必是语句p中的x,那么在p是q的充分条件下,不等式x2-mx+4≥0对任意x∈(0,3)恒成立也就无从说起,当然参考答案(包括正方答案)也站不住脚了.
商榷2:即便语句p中的x就是语句q中的x,那么语句q中的不等式x2-mx+4≥0恒成立,正如反方的意见,这个不等式是关于x的还是关于m的不等式呢?提供的参考答案及正方答案,都是将其看成是x的不等式,为什么要看成关于x的不等式?是否有点牵强?不能因为问题是求m的范围,就把它视为关于x的不等式.
商榷3:这道题的重点不仅考查了充分条件、必要条件的判断,还考查了一元二次不等式在某区间上恒成立问题,但题意表述上人为“挖坑”痕迹明显,似乎有故意将学生往“死路”上引,极不自然,难以让人认同,应该不算一个好题.不妨将该试题修正为:已知p:1<2x<8,q:关于x的不等式x2-mx+4≥0的解,若﹁p是﹁q的必要条件,求实数m的取值范围.这样不容易引起歧义,学生也容易读得懂,下得了手.
五、命题建议
1.别让试题的表述成为学生解答的路障
以检查学生学业情况的一份试卷只有确保每一道试题本身科学无误,才能使考查产生最基本的可信度,这也是命题的最基本要求,同时我们命制试题也不能过分追求“新”、“异”,而落入“偏”且“怪”的境地,而该题的命题意图是追求题意简洁还是为了“难”而“刁难”学生呢?我们反对拖沓冗长地表述题意,但题意表述应该在保证内容正确的前提下清楚、简洁、严谨、科学,尽量做到无懈可击,不能过分追求简洁而失去逻辑性与严谨性,试题中不能出现知识性的错误及有争议的地方,一道题,学生读了多次也没有读得懂,甚至连教师理解题意都有困难与分歧,让学生怎么去求解呢?
2.基础年级阶段性试卷难度不宜过高
从问卷调查结果可知,学生对充分条件、必要条件的判断这个知识点已经基本掌握,但仍然丢了分.即使是理解了命题者意图的9名学生中仍然有3人丢了分.其实“简易逻辑”这部分内容重在充分条件、必要条件的判断,但本题命题意图除了判断充分、必要条件外,又着重考查了基本不等式、一元二次方程根的分布、恒成立,甚至还用到含参不等式的解法等问题,这些当然是高考要求,但不是本学期的学习重点,学生的能力也还没有达到,若修正一下如商榷3的表述,放在高三测试,的确是一道好题.但放在基础年级测试,则对教师教学的导向性不好,容易使老师平时上课盲目拔高.在阶段性考试中,有时我们命题下手比较重,160分的试卷学生平均分在80分左右,6道解答题从第一道就开始难,这样不但起不到激励学生学习的作用,反而让学生心理受到打击,也许学生就因这一次考试而失去学习数学的兴趣.事实上,基础年级阶段性考试有别于升学选拨考试,不是高考,是对平时教学情况的一次反馈,是一次过程性检查,目的是让学生达到巩固、理解阶段性基础知识,因此命题标准要符合相应教学要求和新课程标准的要求,而有别于高考要求,千万不能一提到考试就往高考要求上靠,这样得不偿失!
1.南通大学附属中学2014-2015学年第一学期期末试题高二数学(理科).
2.任志瑜.别让高考题的表述成为“路障”[J].数学通报,2014(4).F
