加载速率对层间断裂韧性的影响
2015-04-28李玉龙刘会芳
李玉龙*,刘会芳
西北工业大学 航空学院,西安 710072
连续碳纤维增强树脂基复合材料以其高的比刚度、比强度广泛应用于航空航天领域[1]。尤其在高性能碳纤维高韧性树脂复合材料出现之后,复合材料在飞机结构上的应用由原来的次承力结构发展至机翼、机身等主承力结构[2]。而复合材料层合板T型以及L型加筋结构是复合材料机翼、机身壁板等结构的重要组成部分,用于加强框或者桁条与蒙皮之间载荷传递[3-7]。其中胶接技术由于胶黏剂密度小,对初始结构无损,工艺简便等又是复合材料结构中常用的连接方式[8]。复合材料层合板以及复合材料L型或T型加筋结构中最常见的破坏形式为分层损伤。分层可能源于低速冲击、工艺缺陷、光照以及鸟撞等[9]。复合材料层合板在低速冲击载荷作用下容易发生分层损伤,分层损伤会导致复合材料面内刚度的降低。因此,长期以来在复合材料界一直把冲击后压缩性能(Compression After Impact,CAI)用做复合材料抗冲击和损伤性能的统一表征[2,10]。而胶接结构中的粘结界面也是整个结构中最薄弱的环节之一[10]。复合材料层合板T型或L型加筋结构在受拉伸、压缩以及弯曲作用时会发生脱胶或者分层等破坏。因此研究复合材料层间以及胶接层的断裂特性具有非常高的应用价值。
界面断裂力学已经广泛地应用于层状材料的分层研究中[11-12],层间断裂韧性是衡量材料抵抗层间裂纹扩展(损伤阻抗)的主要参数。Davies和Zhang[13]发现低速冲击下层合板的临界分层载荷与层间断裂韧性之间为正相关关系。在复合材料分层以及脱胶的有限元模拟中,层间断裂韧性是最主要的材料参数[14-15]。因此需要对层间断裂韧性进行深入的了解。
影响复合材料层间断裂韧性的因素有很多,例如基体的韧性、纤维铺向、厚度方向增强、成型方法及成型固化温度等[16]。Compston等[17]研究了4种基体及其纤维增强复合材料的断裂韧性,结果发现基体的韧性以及基体与纤维之间的黏聚力对于复合材料Ⅰ型层间断裂韧性均有影响。复合材料的层间断裂韧性受基体韧性的影响很大。通过添加纳米颗粒对基体增韧,可提高复合材料的层间断裂韧性[18]。树脂基体呈现出黏弹性力学特性,其断裂性质与温度和加载速率有很大的关系[19-22]。胶接结构中,由于其胶接层的主要成分为高聚物,胶接层的力学特性通常会表现出明显的加载速率相关性[8]。粘结界面层以及粘结层材料的力学特性均表现出率相关性,而在复合材料以及胶接层的服役寿命中,经常受到冲击载荷的作用,因此需要研究加载速率对层间断裂的影响。
虽然研究人员做了大量的工作[23-26]推进层间断裂韧性实验测量的标准化[27-28],但是加载速率以及裂纹扩展速度对层间断裂韧性的影响很少被考虑。而且现有文献中加载速率对层间断裂韧性影响的关系还不是很明确,一方面可能由于实验方法的原因。本文的主要目的是对动态加载下层间断裂韧性的测量方法进行综述。
本文主要分为四个部分,第一部分介绍准静态加载条件下层间断裂韧性的测量方法,第二部分对动态加载下层间断裂韧性的实验方法进行综述,第三部分对光学测量技术在层间断裂测量中的应用进行简要介绍,第四部分对文献中加载速率对层间断裂韧性的实验研究结果进行汇总。
1 静态层间断裂韧性的实验方法
层间断裂分为3种基本形式:Ⅰ型(张开型)、Ⅱ型(滑开型)和Ⅲ型(撕开型),如图1所示。3种变形状态可以独立存在,也可以组合存在。研究中常用应力强度因子、能量释放率以及J积分描述裂纹尖端应力场的强弱,这三者在描述断裂时是等价的,是可以互相转换的[11,29]。对于各向异性材料,应力强度因子K与能量释放率G间的关系[30]为
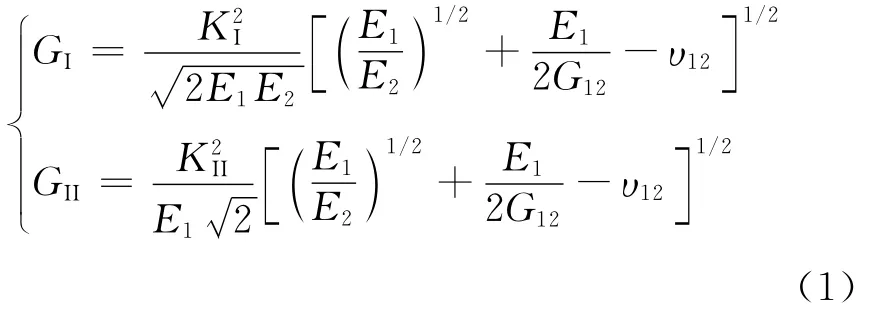
式中:E1、E2分别为1、2方向的拉伸模量;G12为剪切模量;υ12为泊松比。
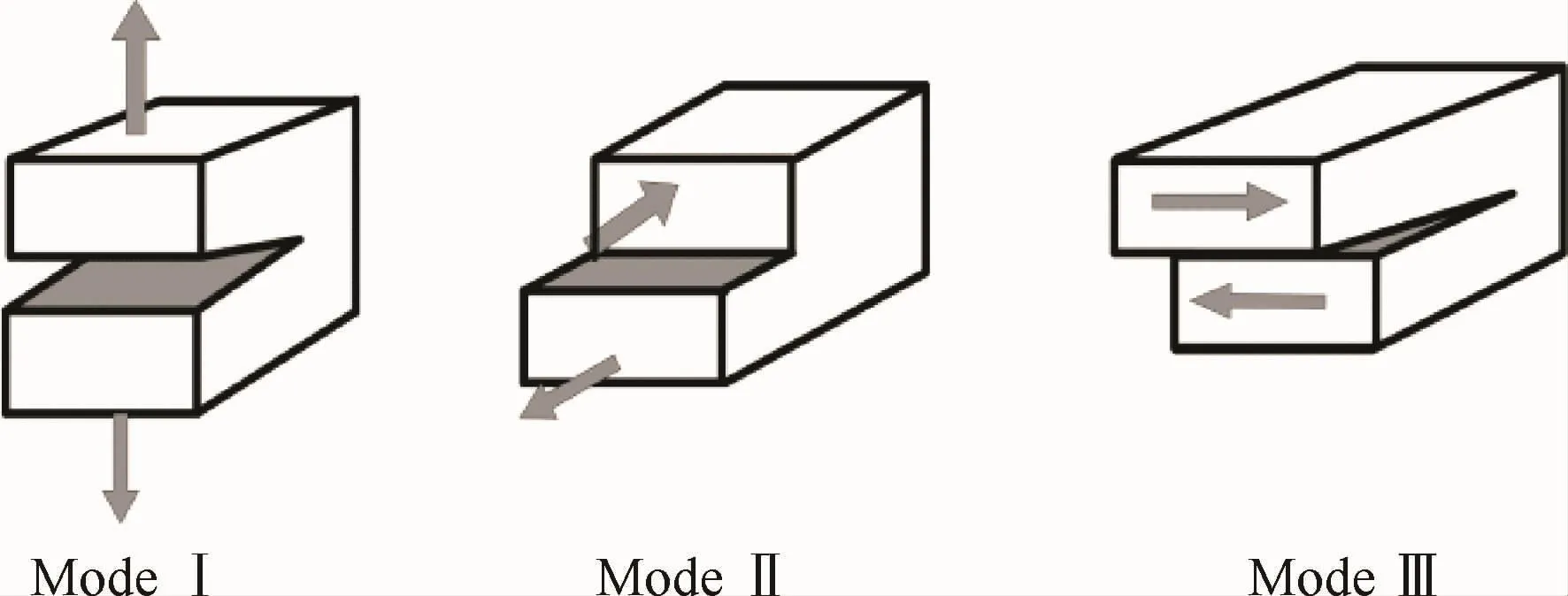
图1 层间断裂模式Fig.1 Interlaminar fracture modes
裂纹起始准则用于判断裂纹是否扩展,以Ⅰ型裂纹为例:
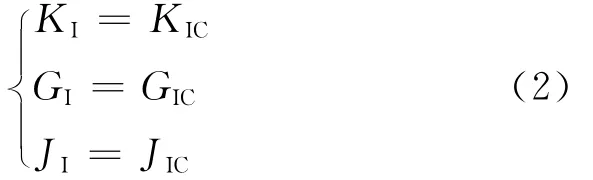
式中:KIC为Ⅰ型临界应力强度因子;GIC为Ⅰ型临界能量释放率;JIC为Ⅰ型临界J积分。这3个参量均为材料常数(断裂韧性),需要通过断裂力学实验测定。
在测量层间断裂韧性时,组合梁是最简单的实验方法。组合梁实验可以非常方便地得到临界能量释放率。利用组合梁方法测量层间断裂韧性时采用的基本公式为Irwin-Kies公式:
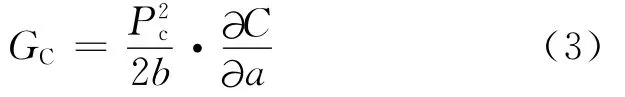
式中:Pc为临界载荷;C=δ/P为载荷线柔度,P为载荷,δ为加载位移;b为梁宽度;a为裂纹长度。测量Ⅰ型层间断裂韧性通常使用双悬臂梁(Double Cantilever Beam,DCB)以及锥形双悬臂梁(Tapered Double Cantilever Beam,TDCB)试样;测量Ⅱ型层间断裂韧性则采用三点加载单边缺口弯曲(3-point End Notched Flexure,3ENF)、四点加载单边缺口弯曲(4-point End Notched Flexure,4ENF)以及端部加载撕裂(End-loaded Split,ELS)试样;Ⅰ+Ⅱ复合型层间断裂韧性则采用混合弯曲(Mixed-mode Bending,MMB)试样。计算柔度时采用的梁类型和边界条件有简单梁固支以及高阶梁弹性支撑[31-32]等。
除此之外,测量层间断裂韧性时还使用巴西圆盘(Brazilian Disk)以及Arcan等试样[33-40]。在进行这些实验时往往需要有限元方法辅助,以标定出试样的几何形状因子fα(α=I,II),其中几何形状因子与试样材料、几何尺寸和加载角度有关[41]。
在测量断裂韧性时,虚拟裂纹闭合法(Virtual Crack Closure Technique,VCCT)经常用于计算复杂载荷边界下裂纹的临界能量释放率。对于2D问题,裂纹尖端如图2所示,临界能量释放率可表示为
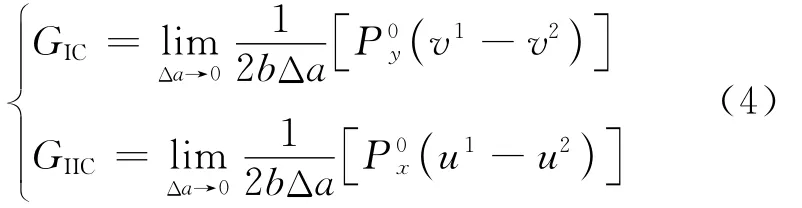
式中:Δa为网格长度;P0x、P0y分别为节点0在x、y方向上的内力;u1、v1分别为节点1在x、y方向上的位移。该方法可扩展至三维网格中[42-43]。
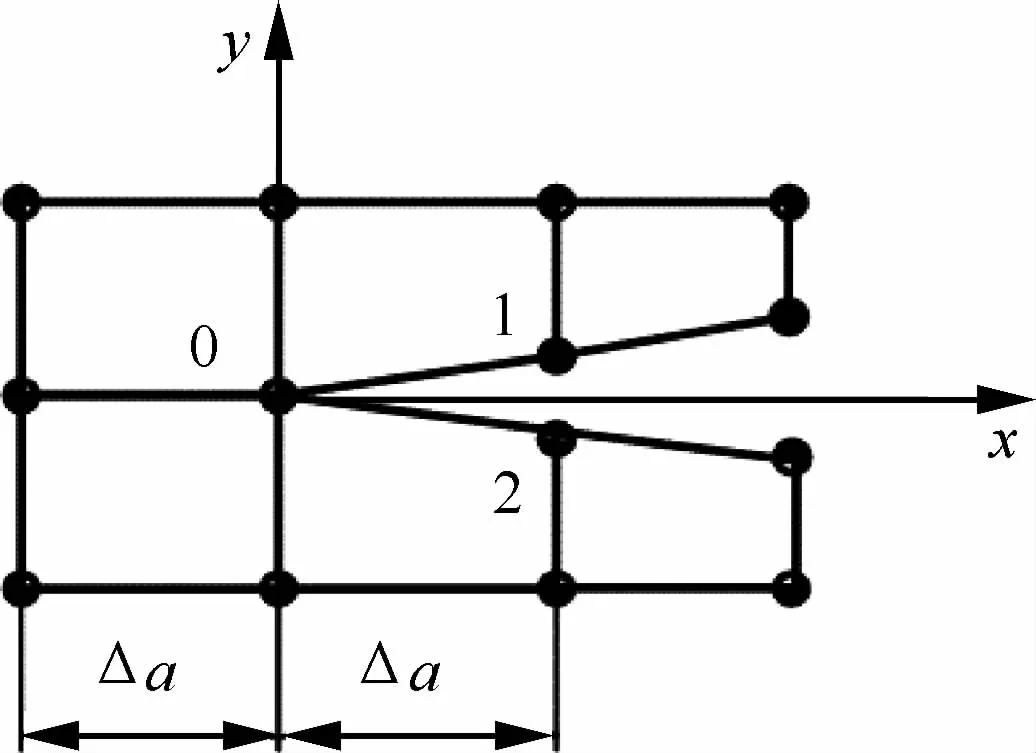
图2 四节点单元裂纹尖端的网格划分Fig.2 Mesh scheme with four-node elements in crack tip area
下面介绍测量Ⅰ型、Ⅱ型以及Ⅰ/Ⅱ复合型层间断裂韧性实验方法,并着重介绍各种实验方法的数据处理。

图3 DCB、WIF以及TDCB试样Fig.3 DCB,WIF and TDCB specimens
1.1 Ⅰ型层间断裂韧性的实验方法
测量Ⅰ型层间断裂韧性最常用的试样为DCB,如图3(a)所示,试样长度为L。DCB实验已经是测量Ⅰ型层间断裂韧性的标准实验[27]。DCB试样也被广泛地应用于胶接层Ⅰ型断裂韧性的测量中[3-4]。
在进行I型层间断裂韧性的测量时,需要注意两个问题[44]:初始裂纹的产生和断裂起始点的判定。层合板的层间断裂韧性受裂纹尖端桥联纤维的影响,使得断裂韧性呈现出R-曲线特性[45],即随着裂纹长度的增加层间断裂韧性增大,因此初始临界能量释放率的测量至关重要。实验中产生初始裂纹的方法有铺设薄膜或I型加载预制裂纹两种。铺设薄膜方法中,薄膜的厚度应小于15μm。因为当薄膜厚度低于该值时,初始临界能量释放率保持不变,厚度大于该值时,初始临界能量释放率随厚度增加而增大[44]。Ⅰ型加载预制裂纹得到的初始临界能量释放率比薄膜预制裂纹得到的值偏大。裂纹起始点的判别方法有3种[27],分别为非线性点、VIS(Visual Observation)点和5%/Max点。非线性点对应载荷位移曲线上的线性偏离点,利用X射线照相技术发现,试样中心处裂纹尖端扩展时对应于该点;VIS点是目测到的试样边缘分层的起始点,5%/Max点为柔度增加5%或最大载荷首先出现的点。这3种方法中,5%/Max点方法得到的结果分散性最小,非线性点方法得到的断裂韧性最保守[44]。
DCB实验数据处理的方法也是研究的重点,早期处理数据的方法有面积法、未经修正的梁理论方法以及柔度拟合法。Hashemi等[46-48]指出利用简单梁理论计算挠度和载荷之间的关系时没有考虑剪切效应以及裂纹尖端梁的挠曲变形的影响。因此,在进行数据处理时需要对裂纹长度进行修正,并提出改进的梁理论(Corrected Beam Theory,CBT)方法,而Hojo等[25]则采用改进的柔度标定(Modified Compliance Calibration,MCC)法。
CBT方法是将对柔度的立方根作为分层长度a的函数绘制坐标图建立两者之间的关系,通过数据拟合直线外推产生与横轴的截距ΔI,临界能量释放率表达式为
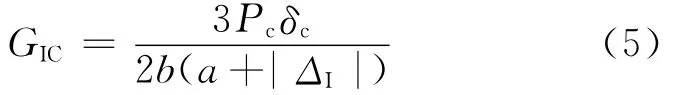
式中:δc为起裂时对应的载荷线位移。另外裂纹长度修正ΔI还可以通过文献[49]中的公式进行计算。
柔度标定法(Compliance Calibration Method,CCM)也用来计算临界能量释放率:

式中:n为lg C与lg a拟合直线的斜率。
MCC方法计算临界能量释放率:
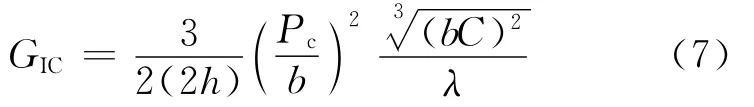
式中:2h为梁厚度,如图3(a)所示;λ为a/2h与(bC)1/3拟合直线的斜率。在加载位移较大时以及采用加载块加载时需要对上述公式进行修正[27,47]。
除了DCB试样,研究人员还发展了许多测量Ⅰ型层间断裂韧性的其他实验方法。Kusaka等[50-51]采用如图3(b)所示的楔入型断裂(Wedge Insert Fracture,WIF)试样测量I型层间断裂韧性。WIF试样是DCB试样的压缩形式。作者给出了WIF试样MCC形式的临界能量释放率的表达式为
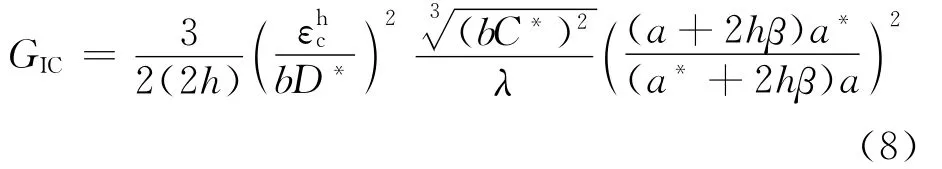
TDCB试样经常用来测量胶接结构I型断裂韧性,TDCB试样的厚度是随裂纹长度变化的,即h=f(a),如图3(c)所示。当试样的厚度满足一定条件时,柔度不随裂纹长度发生变化,临界能量释放率为
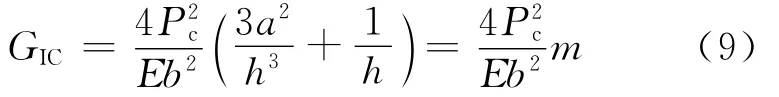
式中:E为臂材料的拉伸模量;m为几何常数。这种实验方法最主要的优点是通过设计试样厚度,使得层间断裂韧性不随裂纹长度改变,因此在实验的过程中不需要测量裂纹的长度。但这种实验的缺点是试样外形复杂,且加工试样的精度要求较高。Blackman等[52]提出校正剪切变形和裂尖挠曲变形的TDCB设计方法:
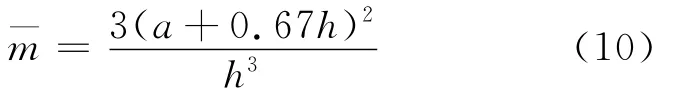
Jose等[53]采用标准紧凑拉伸(Compact Tension,CT)试样测量Ⅰ型层间断裂韧性,如图4(a)所示,应力强度因子表示为
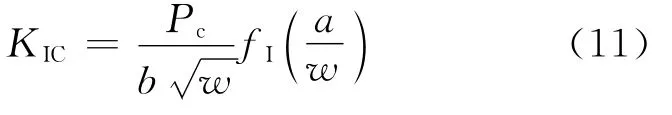
式中:w为试样长度;fI为Ⅰ型断裂的几何形状因子,其具体表达式参见文献[54]。为验证结果的准确性,实验中作者记录裂纹扩展长度、裂纹张开位移以及载荷数据,计算应力强度因子;有限元模拟中将裂纹扩展长度作为位移边界,得到裂纹的张开位移以及临界能量释放率。把实验中得到的参数与数值模拟得到的参数对比,发现式(11)可用于计算层间临界应力强度因子。Sun和Han[55]采用了楔入加载的紧凑拉伸(Wedge Loaded Compact Tension,WLCT)试样,如图4(b)所示,实验中测量载荷和裂纹长度,采用VCCT方法计算层间断裂韧性。
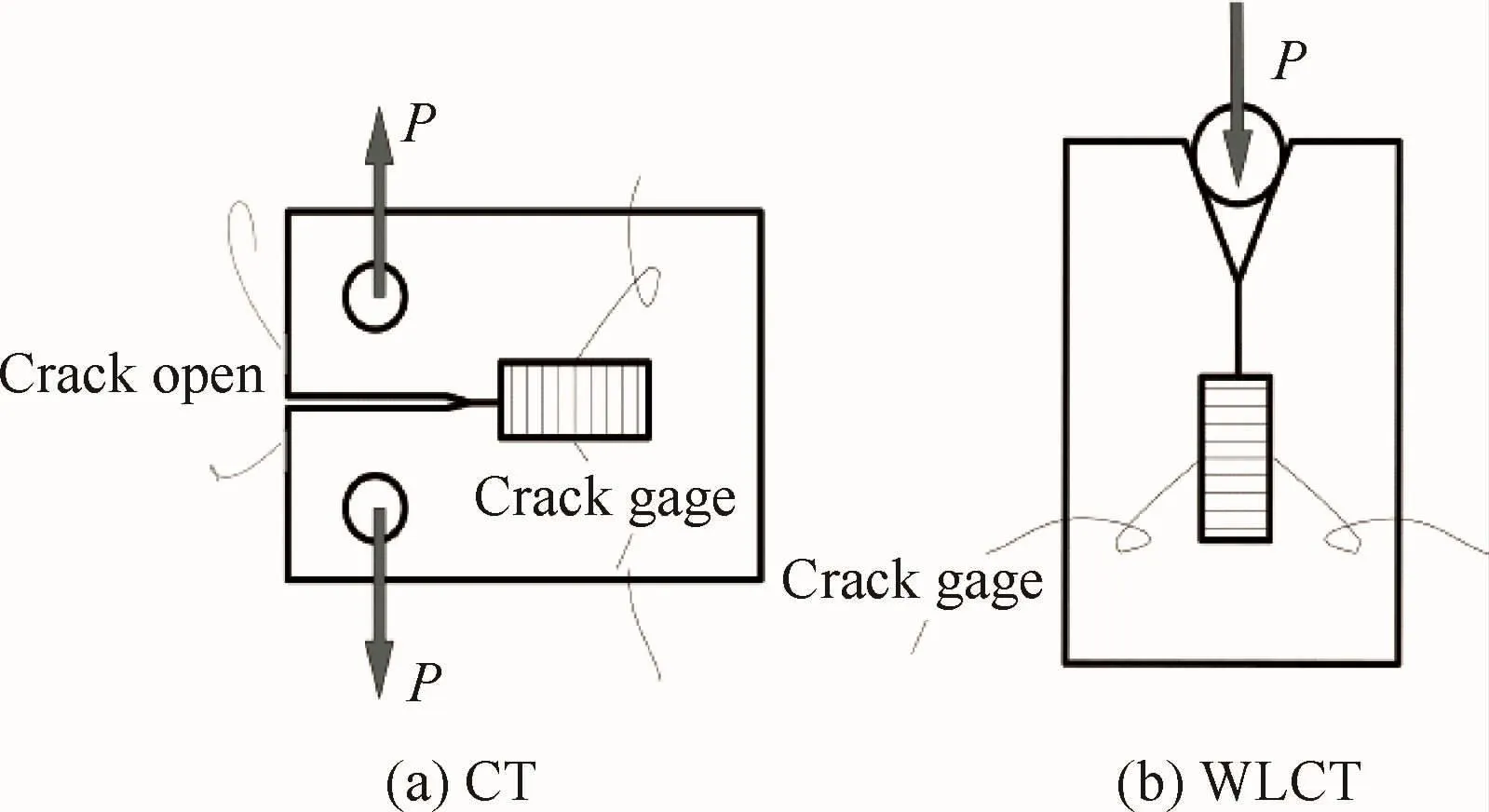
图4 CT与WLCT试样Fig.4 CT and WLCT specimens
Liu等[41]采用四点弯曲加载单边缺口(Single Edge Notch,SEN)试样测量Ⅰ型层间断裂韧性,如图5所示,试样加载点之间的距离为2l,采用相干梯度敏感(Coherent Gradient Sensitive,CGS)干涉方法测量裂纹尖端的应力强度因子,具体实验原理在本文的第3节详细介绍。
准静态加载条件下,测量Ⅰ型层间断裂韧性常用的实验方法有DCB、CT以及SEN等。DCB和CT试样又分为拉伸加载和压缩加载两种形式。SEN试样可采用三点弯曲和四点弯曲加载形式。悬臂梁实验可以通过柔度方法直接计算层间断裂韧性,其他的实验形式则需要有限元方法或光学测量方法的辅助才能得到层间断裂韧性。
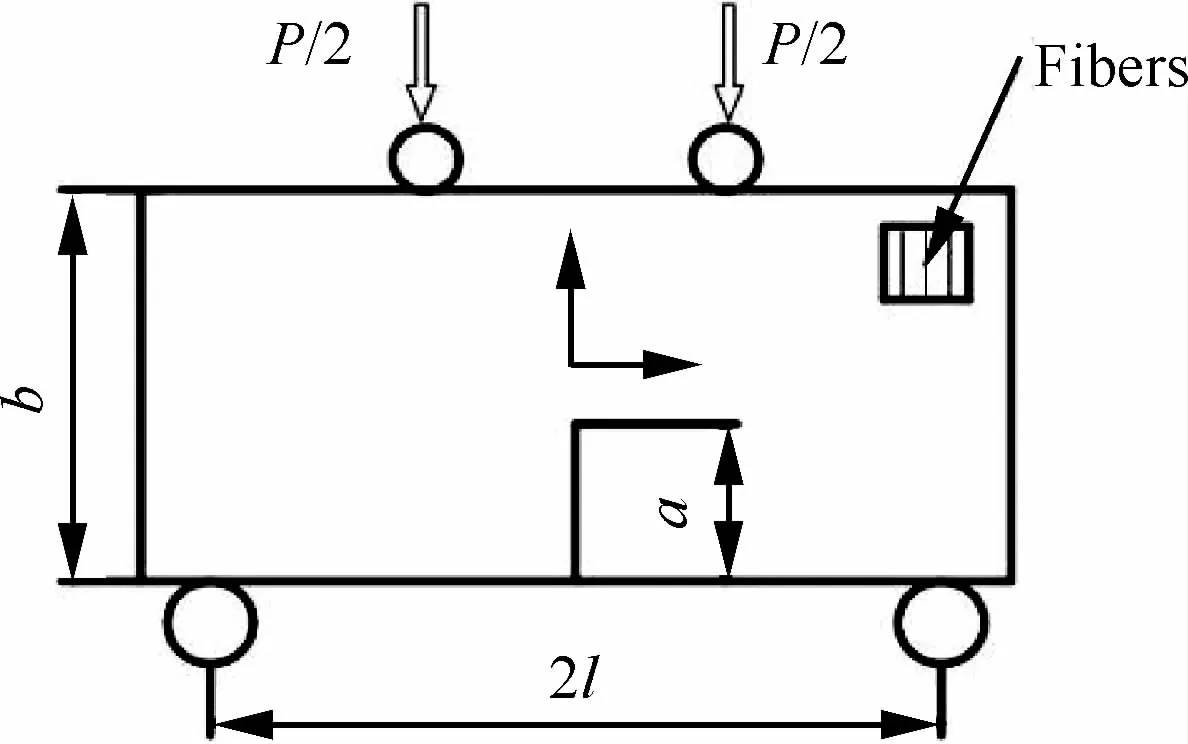
图5 四点弯曲加载SEN试样的示意图Fig.5 Schematic diagram of 4-point loading SEN specimen
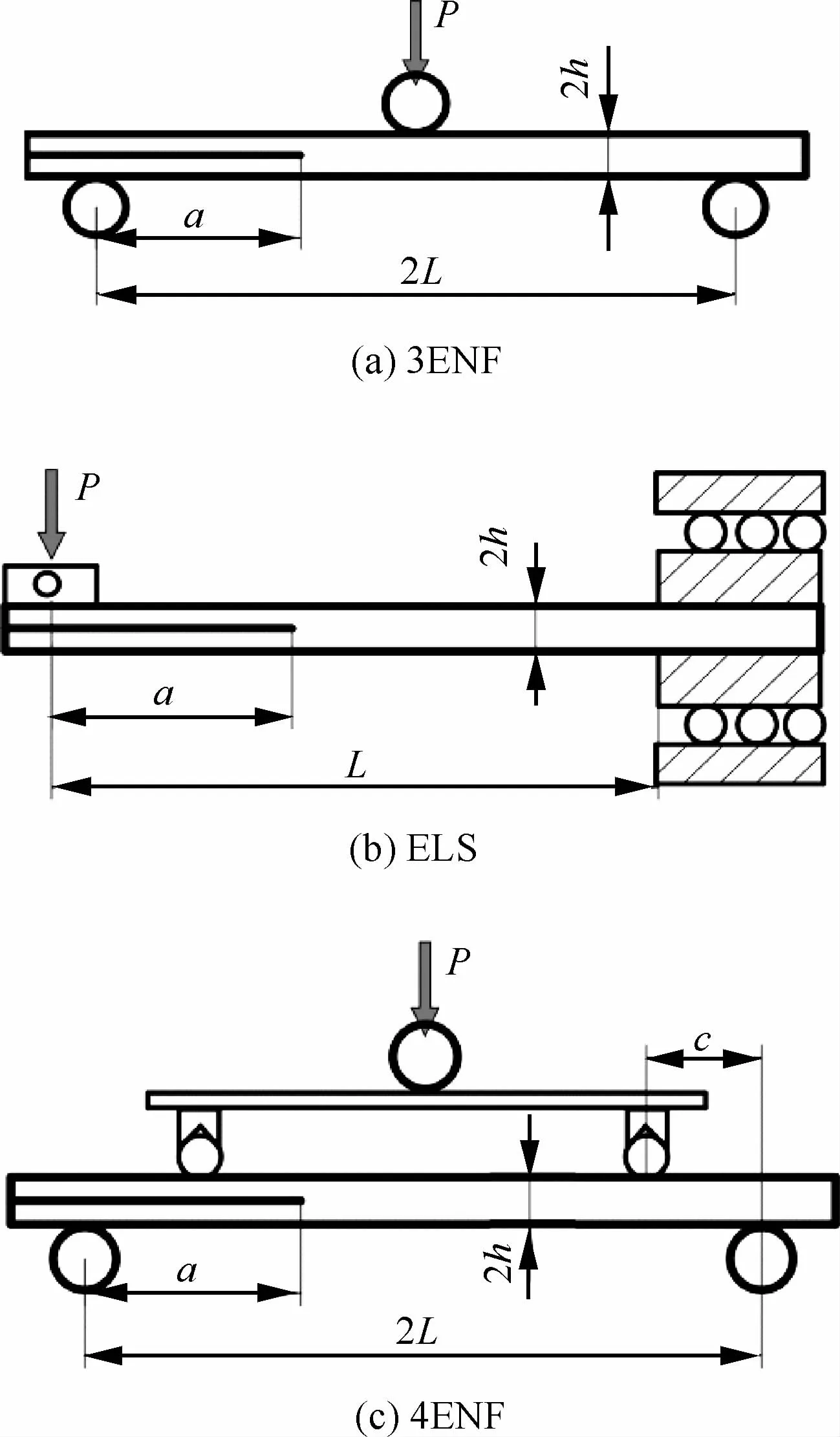
图6 3ENF、ELS和4ENF试样Fig.6 3ENF,ELS and 4ENF specimens
1.2 Ⅱ型层间断裂韧性的实验方法
相对于Ⅰ型层间断裂韧性的测量,Ⅱ型层间断裂韧性测量方法的争议较大,但是Ⅱ型层间断裂韧性更具实际意义。虽然Ⅱ型层间断裂的微观裂纹方向与纤维方向成45°夹角,表现出张开型断裂,但是在宏观工程设计时必须考虑弯矩引起的Ⅱ型滑开型断裂[44]。Davias和Zhang[13]发现层合板临界分层载荷与Ⅱ型层间断裂韧性存在如下关系:

式中:GIIC为层合板的Ⅱ型层间断裂韧性;¯E为面内等效模量;υ为泊松比;H为厚度。此外,Tang等[18]对纳米颗粒增韧层合板复合材料的CAI强度与其Ⅱ型层间韧性进行统计发现:CAI强度与GIIC呈正相关线性关系。
测量Ⅱ型层间断裂最常使用的实验方法有:3ENF、ELS和4ENF,如图6所示,其中,图6(c)中的c为加载点之间的距离。这3种实验方法各有优缺点[56]。3ENF最大的优点是实验方法简单,其缺点是裂纹不稳定扩张,不能得到稳定扩展的层间断裂韧性,产生稳定扩展的条件是a/L>0.7。ELS实验的缺点是夹具复杂,实验的加载位移大,其优点是可以得到初始以及扩展的Ⅱ型层间断裂韧性,该方法产生裂纹稳定扩展的条件为a/L>0.55。4ENF的优点是加载简单,且裂纹稳定扩展,其缺点是实验结果依赖于试样尺寸,且测得的值比3ENF得到的值大。尤其是该方法的摩擦力大,阻碍了它成为Ⅱ型层间断裂韧性测量的标准实验方法[57]。
3ENF数据处理的方法有简单梁理论(Simple Beam Theory,SBT)、CBT、CCM,考虑有效裂纹长度的柔度标定法(Corrected Beam Theory with Effective Crack Length,CBTE),基于柔度的梁理论法(Compliance-Based Beam method,CBBM),其中CCM、CBTE和CBBM得到的结果较好。下面给出几种数据处理方法计算临界能量释放率的公式。
1)SBT:

2)CBT:

式中:L为试样的跨度的一半,如图6(a)所示;χ为裂纹长度的修正系数;Γ为与材料弹性参数相关的量,表示为1.18G13,E1、E2为1方向和2方向的拉伸弹性模量,G13为剪切模量;A1、A2为柔度的拟合参数;a0为初始裂纹长度;ae为有效裂纹长度;C0为载荷线初始柔度;Ccorr为校正柔度;C0corr为初始校正柔度。
Hojo等[26]通过测量裂纹长度负反馈控制3ENF实验的加载速率,形成稳定裂纹扩展的单边缺口实验(Stabilized End Notched Flexure,SENF)。SENF的数据处理方式与ENF完全相同。
对于ELS试样处理数据时不能忽略大变形修正,方法同样有:SBT,CCM,CBT,CBTE以及CBBM。计算临界能量释放率的公式为
1)SBT:
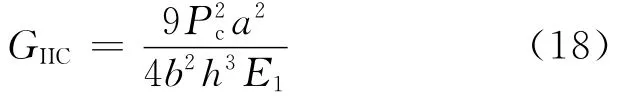
2)CBT:

3)CBTE:

式中:L为试样的长度,如图6(b)所示。ELS实验同样可以采用CCM,与ENF实验的公式相同。
4ENF测量技术还不够成熟,其试样的几何尺寸、夹具的柔度以及数据处理的方法均会对测量结果造成影响[58]。Davidson等[58]研究发现,对于该种试样,利用非线性有限元方法直接计算断裂能量能得到较准确的断裂韧性,但是该方法较复杂。同时作者发现夹具刚度大、跨度小时,使用CCM处理实验数据能得到较准确的临界能量释放率。CBT和CCM为4ENF实验常用的数据处理方法,其计算断裂韧性的公式为
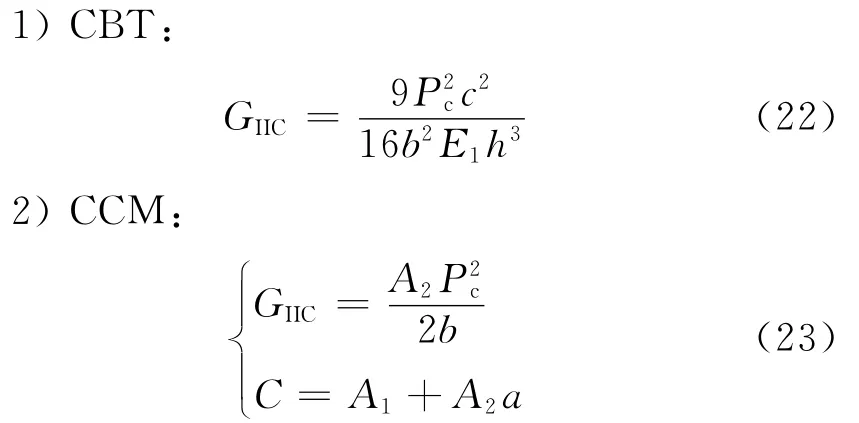
测量Ⅱ型层间断裂韧性的方法还有中心缺口和两端缺口的弯曲实验。计算Ⅱ型层间断裂韧性的方法基本为利用梁理论计算试样的柔度。由于Ⅱ型断裂时层间基体或者层间胶黏剂会产生较大塑性变形以及微裂纹,因此在计算柔度时需要对裂纹长度进行修正,以考虑断裂过程区的影响。Ⅱ型层间断裂韧性一般不会表现出R-曲线特征,但是韧性基体复合材料或胶黏层的Ⅱ型层间断裂韧性与基体层或胶黏层的厚度有较大的关系。
1.3 Ⅰ/Ⅱ复合型层间断裂韧性的实验方法
在实际的结构中,由于载荷分布不对称、裂纹方位不对称、材料各向异性等因素,层间断裂一般为Ⅰ型和Ⅱ型同时作用,因此测量Ⅰ/Ⅱ复合型层间断裂韧性具有广泛的应用价值,复合型层间断裂的能量释放率为Ⅰ型和Ⅱ型的叠加:

混合度也可使用应力强度因子表示。大量实验研究表明界面断裂韧性强烈依赖于混合度,因此需要测量不同混合度下的层间断裂韧性。
复合型断裂下,裂纹扩展准则可采用幂准则以及Benzeggagh-Kenane(B-K)准则描述。幂准则为
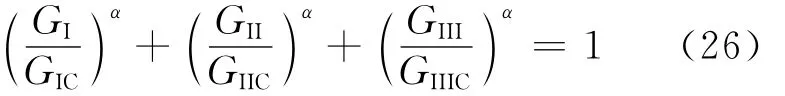
式中:α为实验拟合参数;GIII为III型断裂的能量释放率;GIIIC为纯III型层间断裂的临界能量释放率。B-K准则表示为
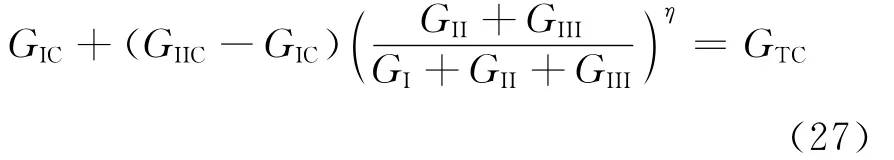
式中:η为实验拟合参数;GTC为复合型断裂韧性。
测量Ⅰ/Ⅱ复合型层间断裂韧性最常用的方法为MMB实验[24,28]。除此之外,还有固定比例混合型弯曲(Fixed-ratio Mixed Mode,FRMM)、混合断裂挠曲(Mixed Mode Flexure,MMF)、单臂弯曲(Single Leg Bending,SLB),搭接剪切裂纹(Crack Lap Shear,CLS)、单悬臂弯曲(Single Cantilever Beam,SCB)、非对称双悬臂梁(Asymmetric Double Cantilever Beam,ADCB)以及Arcan和Brazilian等实验方法。下面对上述方法进行简要的介绍。
MMB首先由Crews和Reeder[59]于1988年提出,之后经过一些改进,在2001年MMB成为测量复合型层间断裂韧性的标准实验方法[28]。MMB的实验装置如图7所示,受力分析如图8所示,可看作为DCB和ENF实验的叠加。通过调整c的大小,该方法可实现不同混合度的层间断裂。Bhashyam和 Davidson[60]比较了几种MMB数据处理的方法,发现由Kinloch等提出的等效裂纹长度法最优,该方法同样作为标准数据处理的方法[28]。
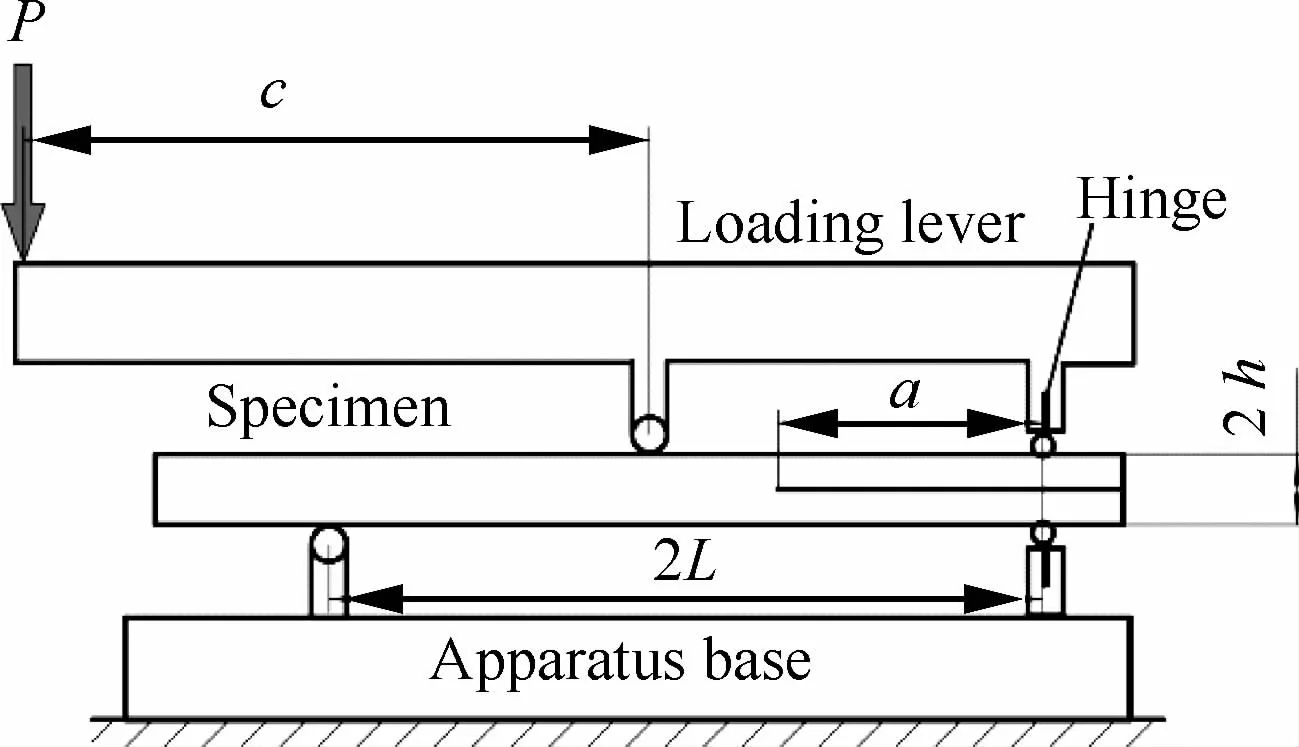
图7 MMB实验装置Fig.7 MMB experiment apparatus
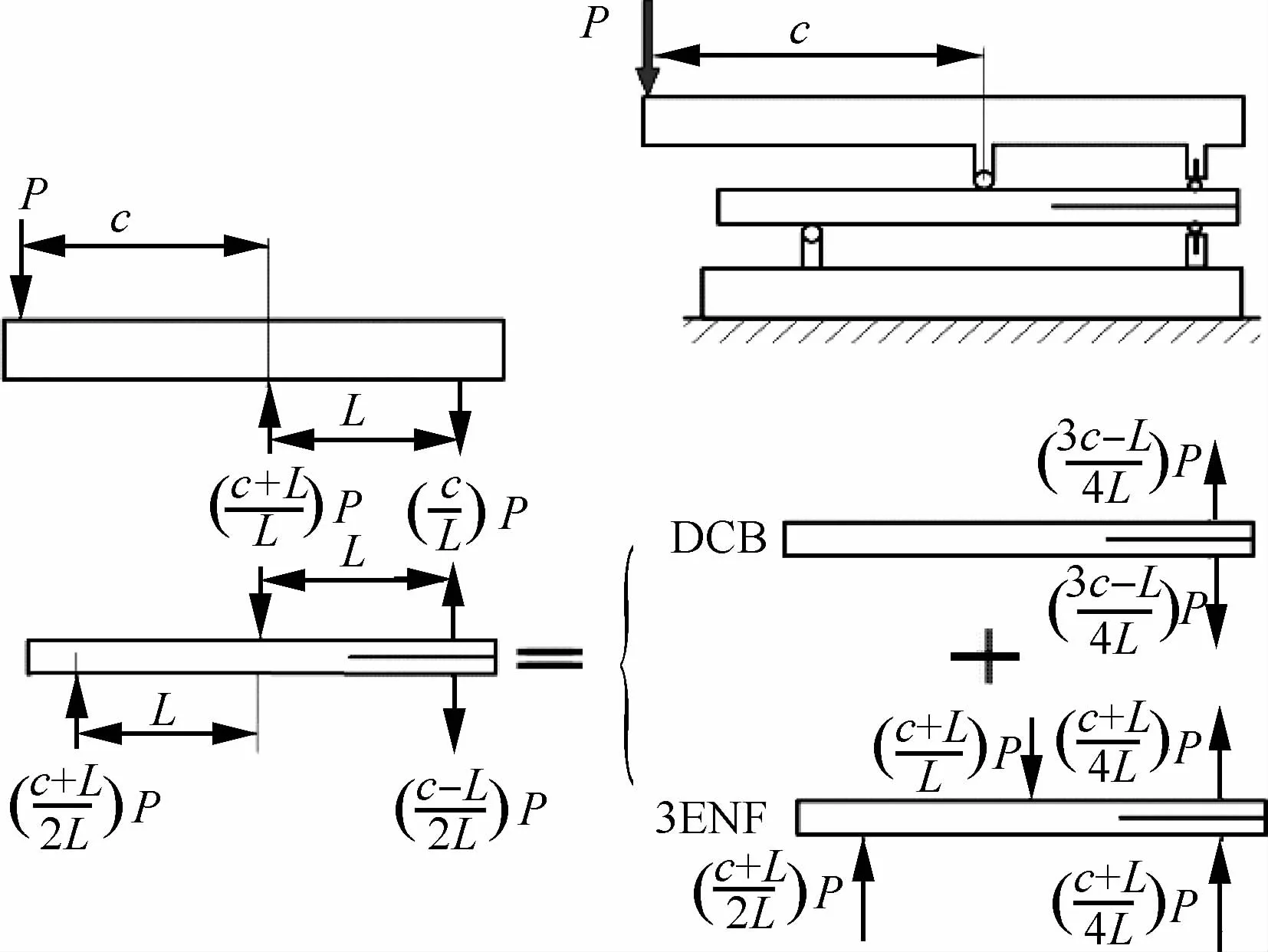
图8 MMB试件受力分析Fig.8 Analysis of loading on MMB specimen
下面给出MMB、FRMM、MMF和SLB实验基于等效裂纹长度方法计算复合型断裂时Ⅰ型和Ⅱ型断裂分量的临界能量释放率。
1)MMB:
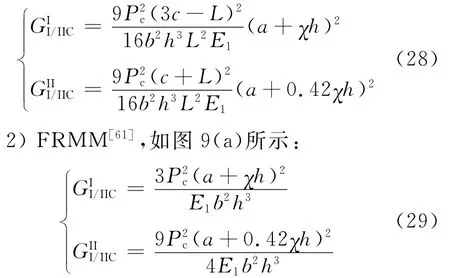
3)MMF与SLB[61],如图9(b)和9(c)所示:
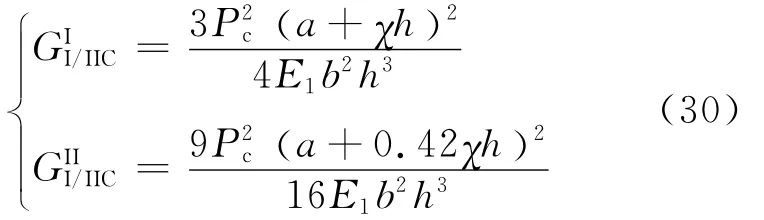
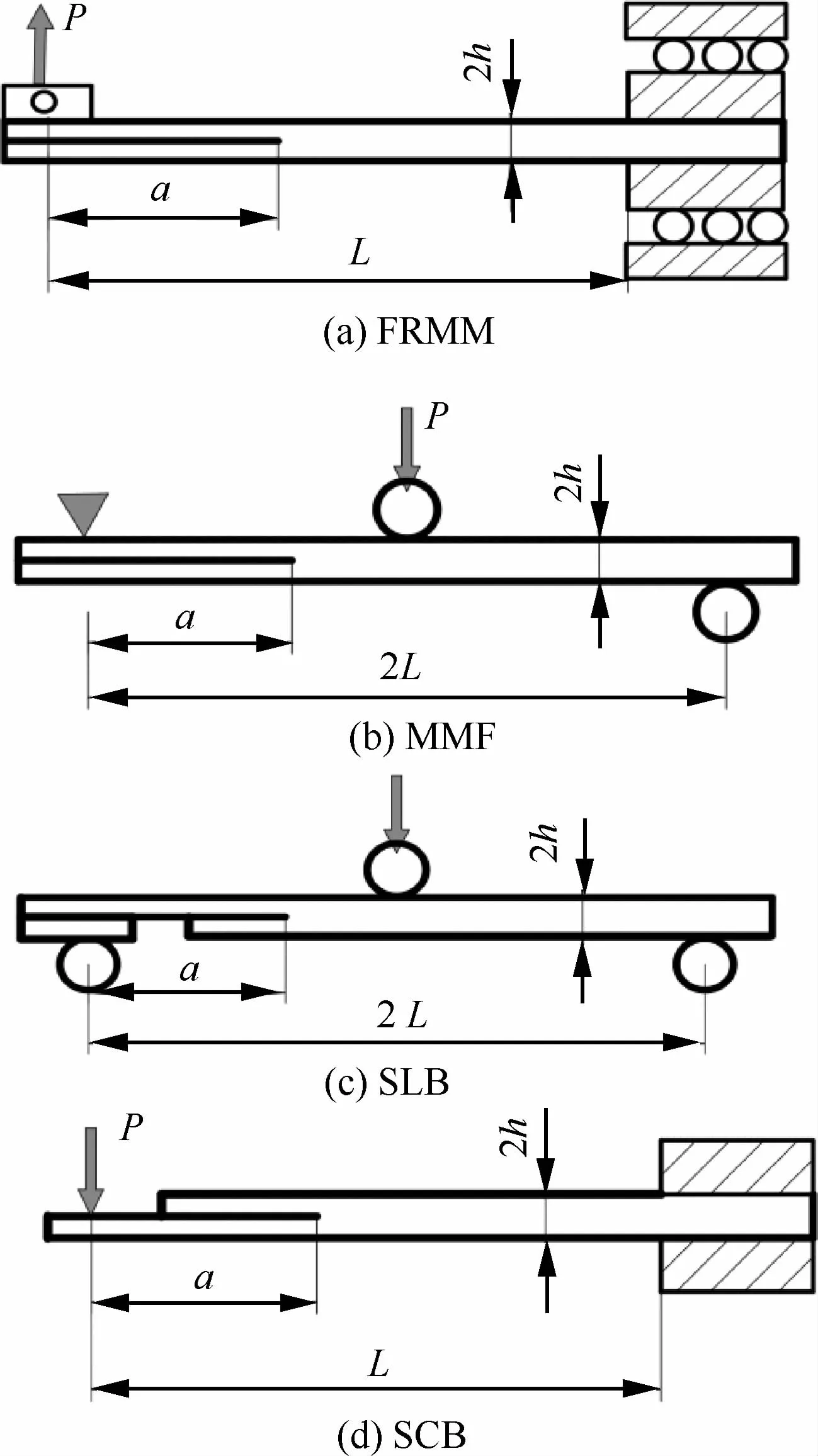
图9 FRMM、MMF、SLB和SCB试样Fig.9 FRMM,MMF,SLB and SCB specimens
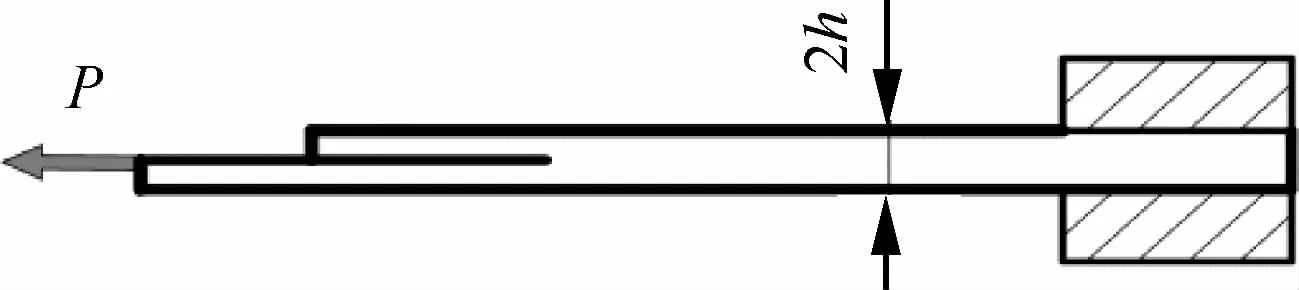
图10 CLS试样Fig.10 CLS specimen
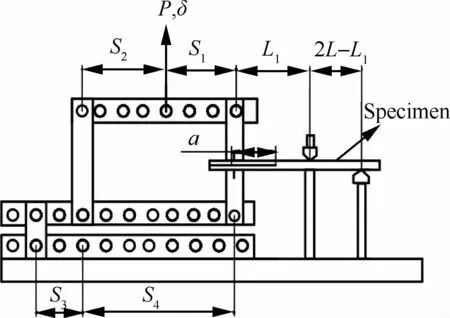
图11 剥离试验[4]Fig.11 Split test[4]
除了采用等效裂纹长度的方法,在计算柔度以及载荷位移关系时,还可以采用高阶梁理论方法,边界条件可采用柔度支撑,Szekrényes和József[62]给出了不同数据处理方法的比较。
CLS实验的加载形式比较简单,如图10所示,但是它存在几个缺点,首先该实验需要有限元分析辅助[63],另外该试样若要达到不同混合度的层间断裂,需要设计不同的铺层方式,即使这样,它所能达到的混合度范围也很小[64]。Mathieu等[65]对CLS试样施加面外的位移约束,并利用数字图像相关(Digital Image Correlation,DIC)技术与有限元模拟相结合的方法,得到裂纹尖端的位置以及断裂混合度,改进CLS试样的断裂混合度约为72°。
剥离试验(Split Test)[4]也被用来测量复合型层间断裂韧性,如图11所示。剥离试验可以看成DCB试样和非对称加载ENF试样的结合,通过调整Si(i=1,2,3,4)的大小可以得到不同混合度的层间断裂。当L1=L时,可直接采用DCB和3ENF的公式计算层间断裂韧性。该方法最主要的特征是调整混合度比较方便,且断裂混合度不随裂纹长度改变而改变[4]。
ADCB实验包括两种形式,第一种形式为载荷非对称,如图12(a)所示,该实验需要复杂的加载系统。这种实验方法的优点是通过改变DCB上施加的载荷可以实现任何混合度的层间断裂(包括纯I型和纯II型断裂)。第二种形式为两个悬臂厚度不等的DCB试样[66],如图12(b)和图12(c)所示。其中,图12(b)中试样的两个悬臂厚度不同,分别为h1和h2,为得到不同的断裂混合度,可以采用不同材料的悬臂。图12(c)中的试样为非对称锥形双悬臂梁(Asymmetric Tapered Double Cantilever Beam,ATDCB)试样,其临界能量释放率可以分为DCB部分和TDCB两部分[66]:
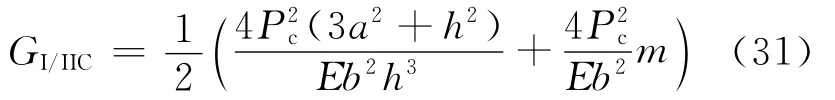
式中:h为DCB的单臂厚度;m为TDCB的几何因子。这种实验测试方法需要利用有限元计算其混合度。
上述复合型层间断裂实验均基于组合梁理论,除此之外,还有很多测量复合型层间断裂的实验形式。下面主要介绍3种测量复合型层间断裂的形式:Arcan试样、巴西圆盘试样以及紧凑拉伸剪切(Compact Tension Shear,CTS)试样。
Arcan试样通过胶黏剂与夹具相连,通过改变拉伸角度得到不同混合度的断裂,如图13(a)所示。对于Arcan试样,应力强度因子的表达式为[67]
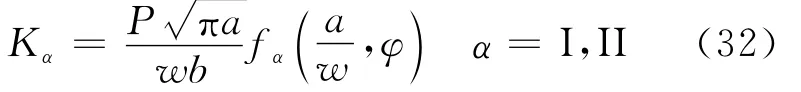
式中:α为断裂类型;a为裂纹长度;w为试样长度;φ为加载角度。作者使用有限元方法计算J积分,根据J积分和应力强度因子之间的关系标定出几何形状因子fα。
Wang和Suo[68]采用巴西圆盘试样测量界面的复合型断裂韧性。Huang[33]和Liu[34]等利用这种试样(如图13(b)所示)测量复合型层间断裂韧性。采用压缩加载形式,通过改变加载角度得到不同混合度的断裂。这种实验同样需要标定出无量纲化几何形状因子fα,对于巴西圆盘试样(平面应力假设下)应力强度因子[34,41,69]为

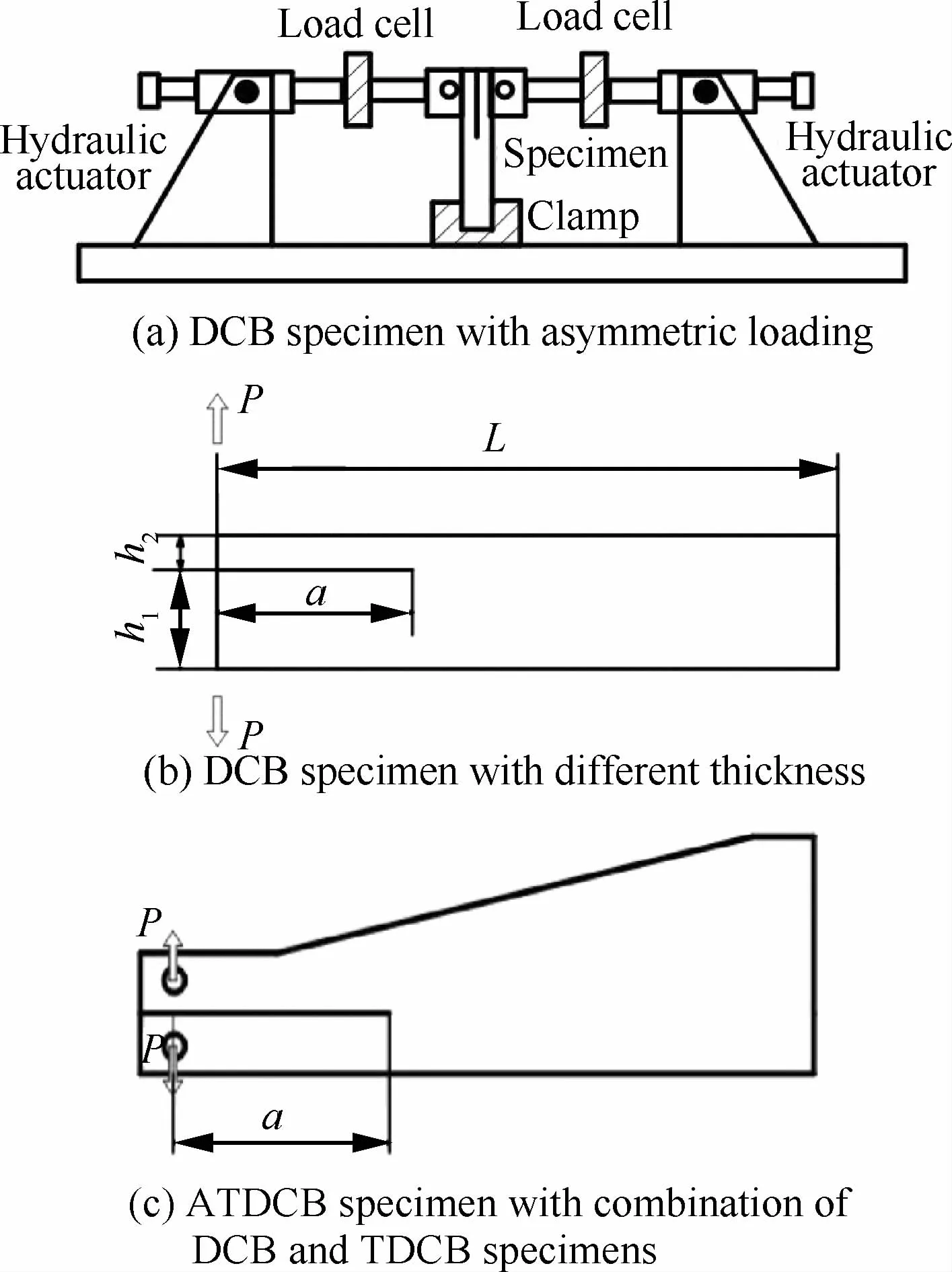
图12 ADCB实验Fig.12 ADCB experiment
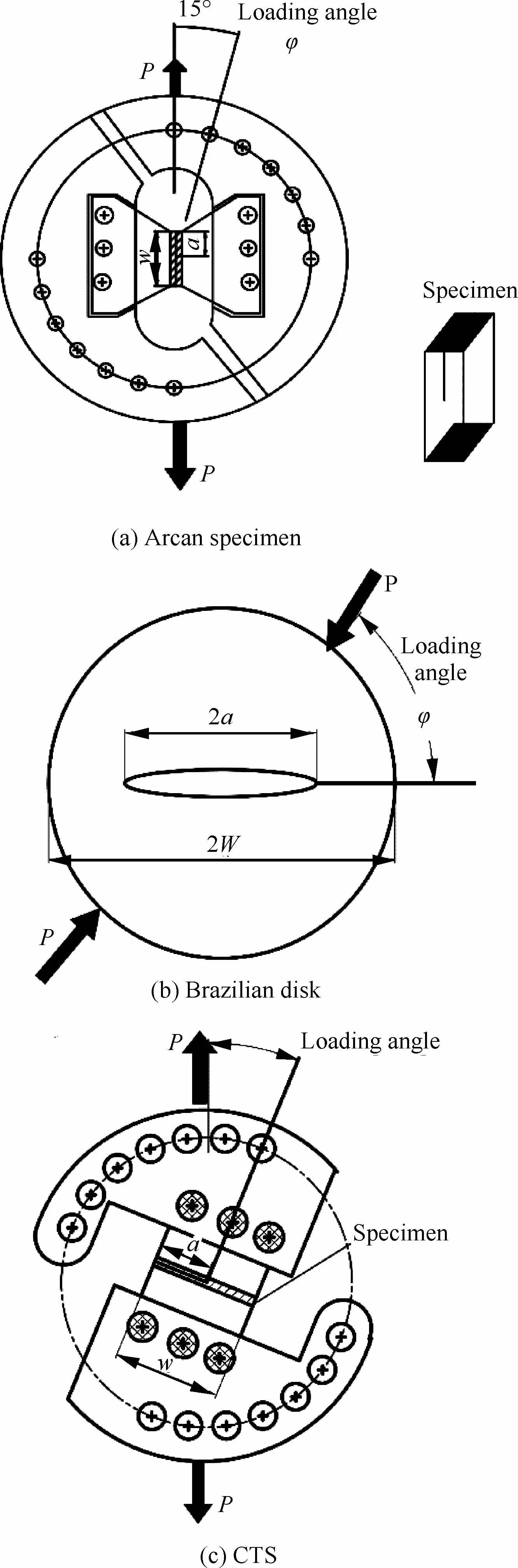
图13 Arcan、Brazilian disk和CTS试样Fig.13 Arcan,Brazilian disk and CTS specimens
CTS试样如图13(c)所示,该试样与Arcan试样类似,文献[70]通过VCCT与实验相结合的方法直接计算能量释放率。除了上述实验形式,非对称四点弯曲SEN试样也被用来测量界面的复合型断裂韧性。
表1中给出了不同复合型断裂实验所能实现的混合度。从表中可以看出,MMB、Arcan、CTS、巴西圆盘试样以及剥离试验可以得到不同混合度的层间断裂,而FRMM、MMF以及SLB所能实现的断裂混合度均约为41°。在利用组合梁测量复合型层间断裂韧性时需要注意裂纹长度的修正以及断裂混合度的计算等问题。

表1 不同断裂实验对应的混合度Table 1 Different fracture experiments’mode mixity
1.4 小 结
准静态层间断裂韧性的测量方法有很多,最常采用的试样是组合梁试样,这种方法求解能量释放率简单方便。但是需要注意的是,利用Irwin-Kies公式计算能量释放率时需要对裂纹长度进行修正。
测量得到的层间断裂通常表现出R-曲线效应,但是R-曲线与试样的尺寸相关,在有限元模拟中需要输入与尺寸无关的材料参数,因此层间断裂测量的重点应该在确定与尺寸无关的材料参数上[45,71]。
此外,本节仅给出了Ⅰ/Ⅱ型层间断裂的实验方法,对Ⅲ型层间断裂韧性进行测量通常采用边裂纹扭转(Edge Crack Torsion,ECT)试样。在三维有限元模拟中需要输入Ⅰ/Ⅱ/Ⅲ复合断裂的准则,因此需要确定Ⅰ/Ⅲ和Ⅱ/Ⅲ等复合型层间断裂的断裂韧性。
2 动态层间断裂韧性的实验方法
在通常情况下,复合材料层合板容易受到面外的冲击载荷,层间裂纹一般表现出动态扩展;Gozluklu等[5]发现复合材料层合板L型加筋即使在准静态加载下,复合材料层间裂纹也会跨声速扩展。因此需要对动态层间断裂进行深入的研究。
动态断裂力学作为断裂力学的一个分支,主要考虑断裂过程中的惯性效应,惯性效应可以由含裂结构态载受动载荷引起,也可由裂纹快速扩展产生。动态断裂力学主要研究两大类问题。第一类问题是含裂体在动态载荷下的起裂问题;第二类是裂纹的快速扩展以及止裂问题。
第一类问题研究的主要内容即为动态加载下裂纹起始的断裂准则,即动态起裂韧性(以I型断裂为例表示为KdIC或GdIC)的测量。现有文献已经表明,裂纹的起裂韧性随加载速率的变化而变化。准静态断裂力学不同,动态应力强度因子不只是材料、试样几何尺寸以及外加载荷的函数,同时为时间t的函数,即Kd(fα,σ,t),α=I,II。动态断裂力学中往往以应力强度因子KI(t)对时间的变化率表示加载速率,即

式中:˙K为应力强度因子表示的加载速率;tf为起裂时间;˙a为裂纹长度扩展速率;σ为外载荷。类似于静态断裂起始判据,Ⅰ型动态起裂判据可表示为
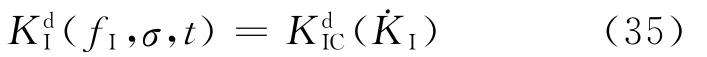
式中:fI为Ⅰ型断裂的几何形状因子。
对于裂纹的动态起裂问题,表征其断裂加载速率的方法有很多,Kusaka等[50-51,72-73]采用能量释放率随时间的变化率作为加载速率的表征:

式中:˙G为能量释放率表示的加载速率;Gd(t)为随时间变化的能量释放率。除此之外,根据能量释放率与应力强度因子之间的量纲关系,加载速率又可表示为

Blackman等[61,74]用加载点位移速率代替动态层间断裂的加载速率,并建议使用高速相机记录试样在加载点的位移,而不能直接采用机器夹头位移。Smiley和Pipes[75]定义距离裂纹尖端一定距离处裂纹的张开速率作为加载速率的表征,该方法存在一定的随机性,且真实的裂纹张开速率比计算的值大得多。
利用高速加载装置是产生动态裂纹起裂最常用的方法。实现动态加载的仪器有:摆锤冲击试验机、Izod冲击试验机、落锤实验机、高速试验机、霍普金森压杆(Hopkinson Pressure Bar,HPB)以及气炮等。本节主要的内容就是对动态起裂韧性测量的实验方法进行综述。
第二类问题主要研究裂纹的失稳扩展判据、快速扩展裂纹的分岔及止裂判据等。动态断裂失稳扩展过程中,可利用裂纹长度扩展速率˙a表示加载速率,且动态断裂的扩展断裂韧性与裂纹速率有关。Ⅰ型动态裂纹扩展的判据可表示为

研究该问题时,一般在裂纹尖端加工止裂孔或止裂胶膜[76-78]等,目的是让试样储存足够的能量,以供裂纹快速扩展,然后准静态加载至裂纹的失稳扩展。这种方法不能研究失稳裂纹的起始扩展问题,不能测试裂纹的失稳扩展判据。对层间裂纹动态扩展研究的文献较少,在本节的第四部分对其进行综述。
本小节首先对常见的Ⅰ型、Ⅱ型以及Ⅰ/Ⅱ复合型动态层间断裂起裂韧性的测量方法进行综述,着重介绍试样类型、加载形式以及数据处理方法,然后介绍层间裂纹动态扩展的研究方法。
2.1 Ⅰ型动态层间起裂韧性的实验方法
实现Ⅰ型动态层间断裂最常用的试样仍是DCB试样,加载形式为拉伸加载,只是加载的速率比准静态加载速率有所提高。这种方法的优点是能量释放率计算方便。
实现高的加载速率有以下几种方法:①采用一般试验机进行高速加载[75,79-80],该方法简单易行,但其加载速率受试验机最大加载速率的限制,加载速率一般在1 m/s以下;②通过设计复杂的加载装置,放大试验机的加载速率,Hug等[78]采用如图14所示的装置,将原有试验机的垂直位移转换为水平位移,水平加载的速率是垂直加载速率的4倍,能达到的最大加载速率为1.6 m/s,Joannic等[81-82]采用如图15所示的加载装置,可达到的最大加载速率为2.4 m/s;③采用高速试验机,Blackman等[74,83]采用高速试验机对DCB试样进行加载,如图16所示[61],最大的加载速度可达15 m/s;④采用落锤加载DCB试样[84],如图17所示[84]。

图14 高速加载装置[78]Fig.14 High-speed loading machine[78]
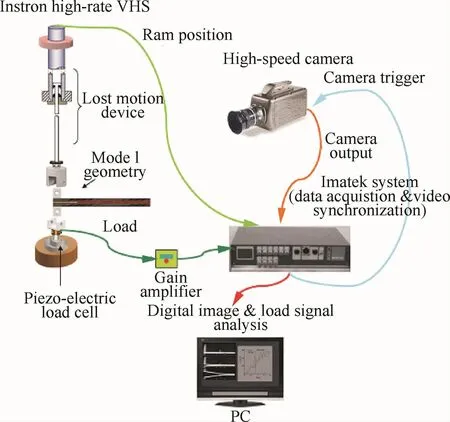
图16 高速加载试验装置以及数据采集系统[61]Fig.16 High-speed loading apparatus and data acquisition system[61]
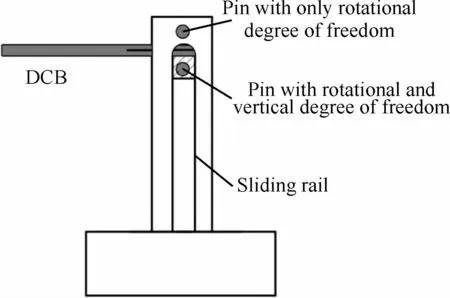
图17 落锤动态加载试验装置及DCB试样[84]Fig.17 Drop hammer dynamic loading apparatus and DCB specimen[84]

表2 断裂类型以及断裂分析要素[83]Table 2 Types of fracture and features of their analyses[83]
与准静态加载时不同的是,动态加载需要将试样的动能考虑到能量释放率的计算中:
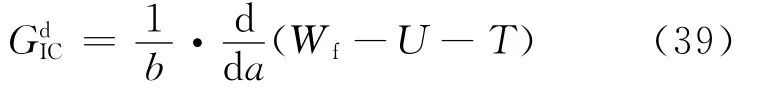
式中:Wf为外载荷总功;U为试样的变形能;T为试样的动能。
Smiley和Pipes[75]给出了DCB试样的动能对裂纹长度微分的表达式:

式中:ρ为试样密度;˙δ为载荷线位移速率;T为试样动能。Hug等[78]发现对于DCB试样,加载速率为3 m/s时,动能对断裂韧性的影响小于1%,因此动能的影响可忽略不计。
Blackman等[61,74,83]使用高速试验机分别对DCB和TDCB试样进行实验。在研究动态加载时,根据具体的裂纹扩展类型,分别考虑试样的动能的影响。首先作者将裂纹分为4种分析类型:慢速稳定扩展(类型1)、慢速不稳定扩展(类型2)、快速稳定扩展(类型3)以及快速不稳定扩展(类型4),这4种方法的载荷测量的准确性以及动能是否需要考虑见表2[83]。
在计算层间起裂韧性时,按照流程对裂纹的分析类型进行判定:①首先画出裂纹长度随t的变化图,利用线性回归分析,若R2>0.95,定义裂纹为稳定扩展,反之定义裂纹为不稳定扩张;②对于稳定扩展裂纹,画出裂纹长度与时间t的关系图,得到裂纹扩展速率,确定准静态断裂韧性GIC和动态断裂韧性GdIC,若(GIC-GdIC)/GIC<5%,则认为裂纹为类型1,否则为类型4;③对于不稳定扩展裂纹,画出裂纹长度a与时间t的关系图,得到粘结阶段(˙a=0)结束时裂纹长度的扩展速率,确定准静态断裂韧性GIC和动态断裂韧性GdIC,若(GIC-GdIC)/GIC<5%,则认为裂纹为类型2,否则为类型3。TDCB实验数据处理与DCB相似,不再赘述。
当裂纹快速扩展时,测得的载荷值不再准确,因此计算层间断裂韧性时不能直接使用载荷信号。对于类型1和类型2,层间起裂韧性的计算方法与准静态相同,对于类型3[83]:
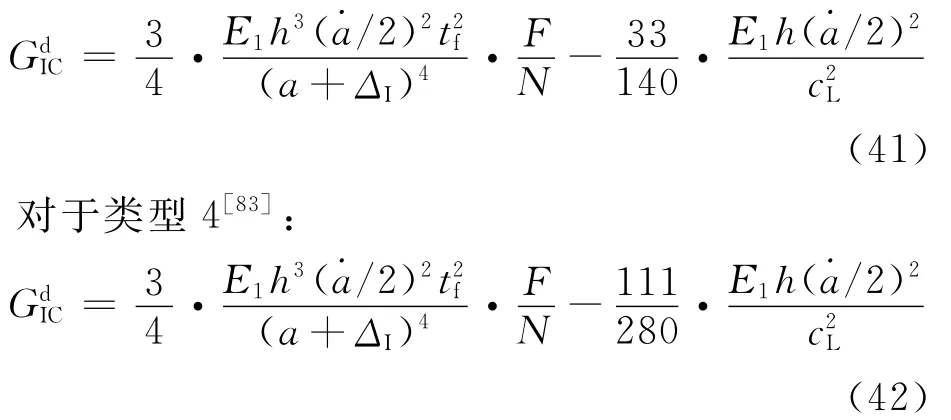
式中:cL为纵波波速;F为大位移修正系数;N为加载块修正系数。
利用如图17所示的加载形式对DCB试样进行加载的缺点是,在高速情况下,试样加载不对称,断裂形式为Ⅰ/Ⅱ复合型断裂。
除了拉伸形式的DCB实验之外,还有动态压缩形式的DCB实验:①WIF试样,Kusaka等[50,73]采用HPB加载复合材料层合板 WIF试样,加载速率可达20 m/s,Thouless等[85-86]采用落锤加载WIF试样,测量胶接层的动态断裂韧性;②采用落锤楔入加载DCB试样[87-89]。
Kusaka等[50,73]采用HPB加载WIF试样,如图18所示[50],最大的加载速率可达到20 m/s。试验中,作者利用波形整形器减小高速加载时试样的振动,数据处理方法与准静态数据处理方法相同。
Thouless等[85-86]采用落锤加载 WIF试样研究胶接层的断裂韧性,如图19所示[85],试样的单臂厚度为h,加载速率为0.5~5 m/s,假设悬臂材料的应力应变曲线可表示为幂形式σ=Aεn,A为拟合参数,计算层间断裂韧性的方法为

式中:Rf为起裂时臂变形后的曲率。
Xu和Dillard[88]采用落锤加载DCB试样,如图20所示,DCB上装有两条平行的加载钉,冲击夹头上安有两个透明的三角形夹具,动态加载的同时可观测裂纹的扩展。由于动态加载下载荷不准确,作者采用裂纹张开位移计算层间断裂韧性:
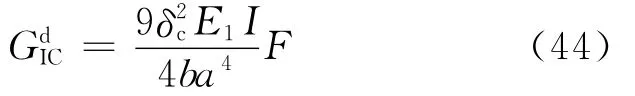
式中:I为截面惯性矩。
上述实验方法均属于DCB实验,且使用的数据处理方法均为解析方法,当加载速率较小时,不考虑试样动能的影响[75,78-79,84,88],当裂纹高速扩展时,对于不同的裂纹扩展类型,数据处理时分别进行考虑[83,90]。Sun和 Han[55]采用 HPB加载WLCT试样,如图21所示,利用有限元方法与实验相结合的方法测量Ⅰ型动态层间起裂韧性。有限元模型中的载荷边界为透射杆得到的力;具体的计算方法为改进的裂纹闭合法(Modified Crack Closure,MCC)[55]:

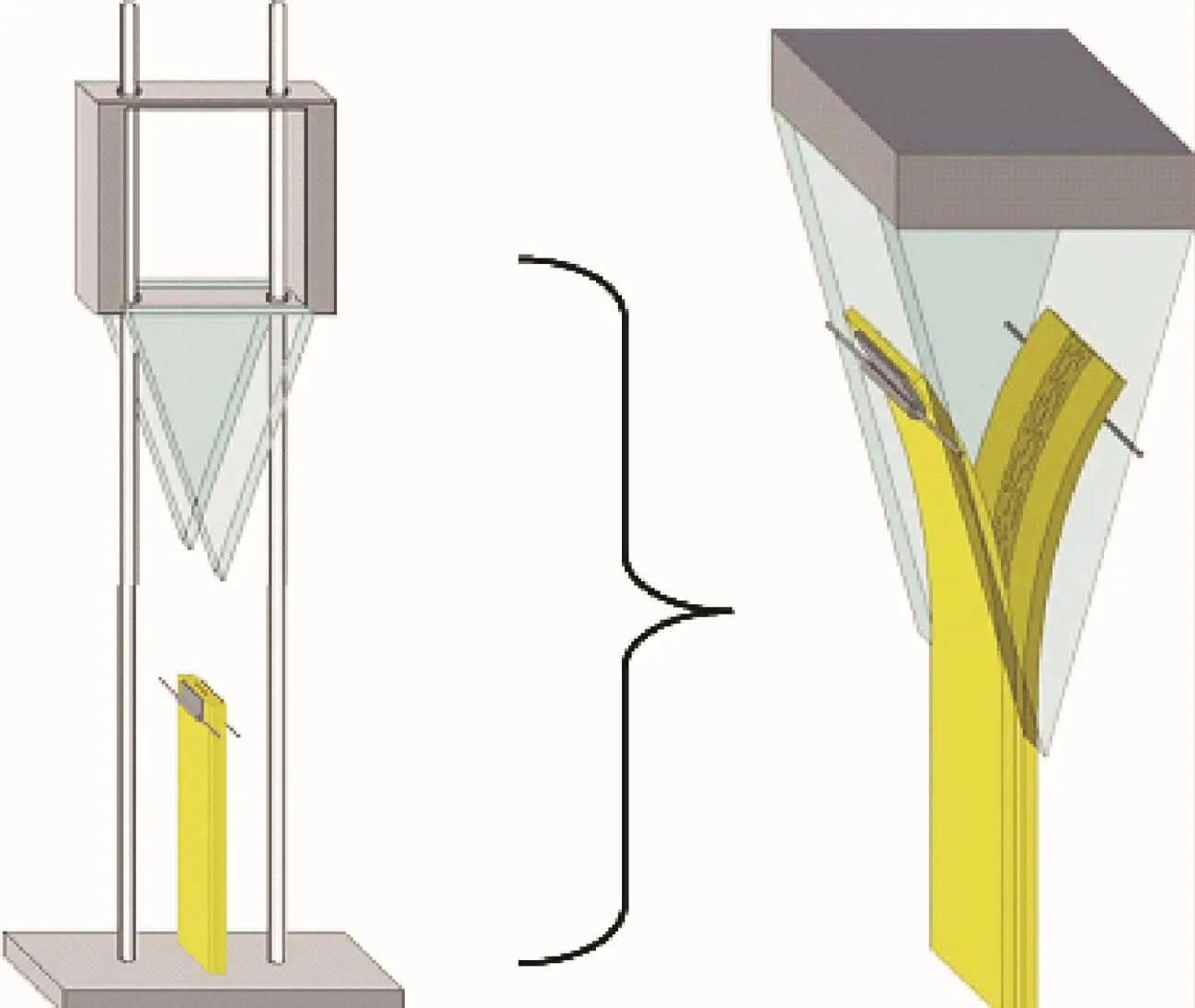
图20 落锤实验装置以及DCB试样[88]Fig.20 Drop hammer experiment apparatus and DCB specimen[88]
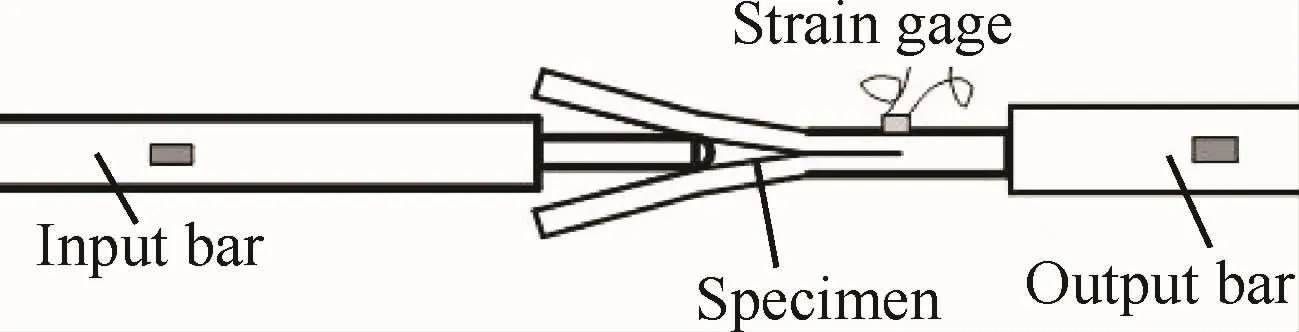
图18 动态WIF实验装置[50]Fig.18 Dynamic WIF experiment apparatus[50]

图19 落锤冲击加载及WIF试样[85]Fig.19 Drop hammer impact loading and WIF specimen[85]
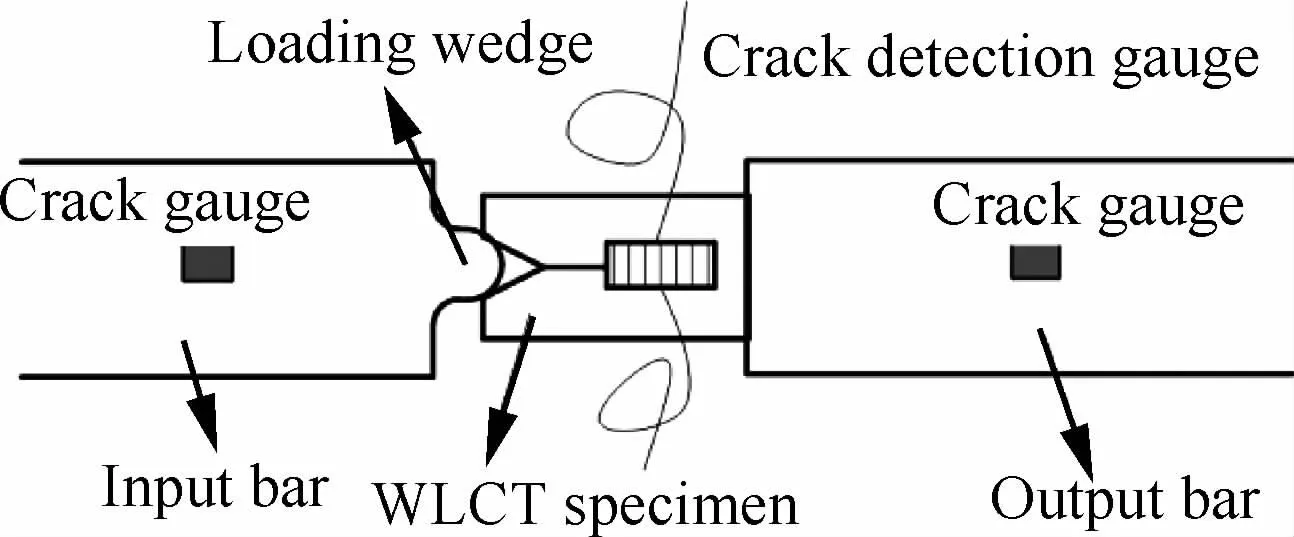
图21 HPB动态加载及WLCT试样[55]Fig.21 HPB dynamic loading and WLCT specimen[55]
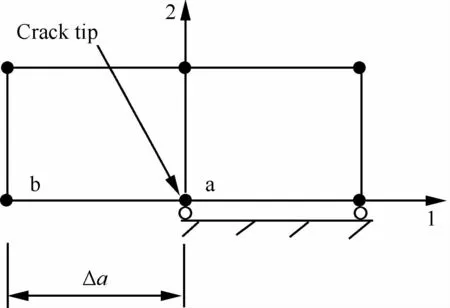
图22 MCC方法中的单元和节点Fig.22 Elements and nodes used in MCC method
为研究界面的动态层间断裂韧性,Syn[91]设计一种四点弯曲试样,如图23所示,加载装置为HPB,四点弯曲加载裂纹尖端只受弯矩的作用,试验中采用石英压电薄膜测量动态载荷,动态临界应力强度因子[91]为
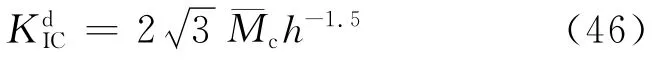
式中:¯Mc为起裂时单位厚度上裂纹尖端处的弯矩;h为图23中入射杆与透射杆加载点之间的距离。
Wu和Dzenis[92]采用如图24所示的加载装置测量动态层间断裂韧性,其中加载类型为三点弯曲加载,加载装置为HPB。作者采用了数值、解析与实验相结合的方法计算层间断裂韧性。首先试验过程中确定入射杆上的加载波形,确定载荷谱P(t),同时利用监裂应变片确定裂纹起始时间;然后进行有限元分析,载荷边界条件为载荷谱P(t),位移边界条件与试验中边界相同,计算时间的终止点为试验中裂纹起裂的时间点,计算得到裂纹尖端位移场的分布;第三步提取出数值分析的裂纹尖端张开位移(Crack Opening Displacement,COD),如图25所示,在θ=π时,可得到裂纹尖端各点对应的COD(uxi,uyi),其中uxi表示i点在x方向的滑移位移,uyi表示i点在y方向的张开位移。在Ⅰ型张开裂纹下,uxi为0,uyi为
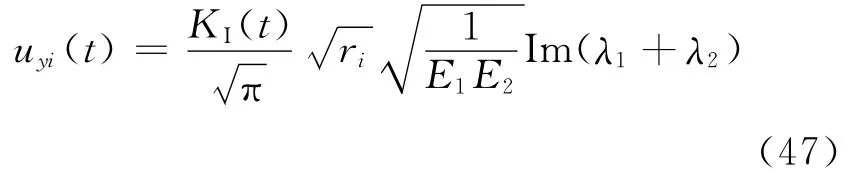
式中:KI为需要计算的应力强度因子;ri为i点距裂纹尖端的距离;E1、E2为1、2方向的弹性模量;λ1、λ2为材料参数。在得到应力强度因子后,通过式(1)得到相对应的能量释放率。
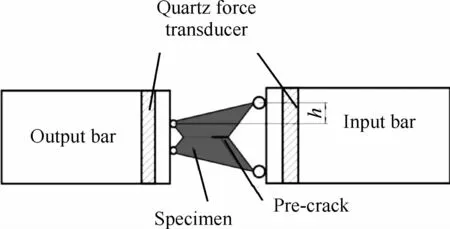
图23 HPB加载4点弯曲试样[91]Fig.23 HPB loading 4-point bending specimen[91]
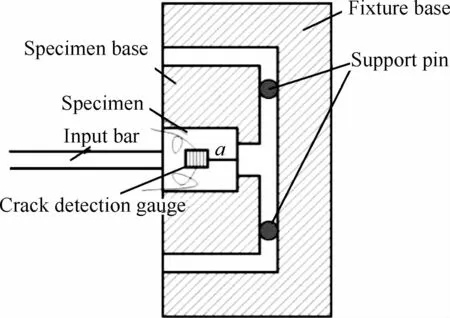
图24 HPB加载三点弯曲试样[92]Fig.24 HPB loading with 3-point bending specimen[92]
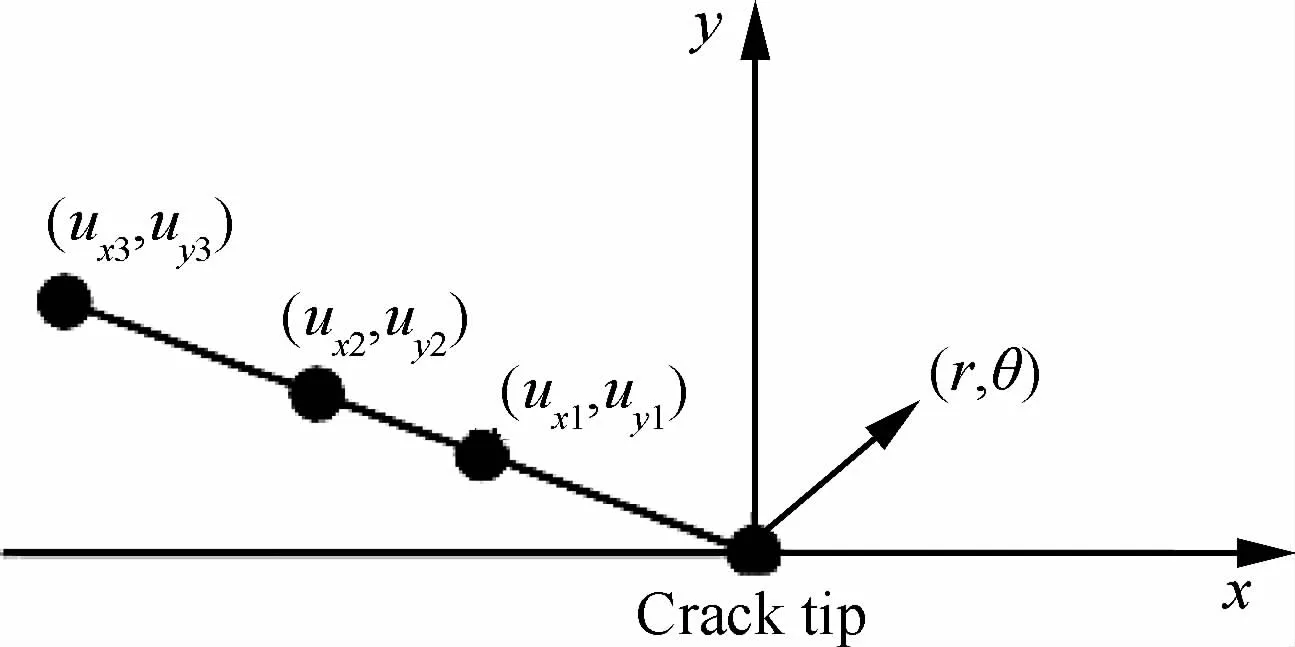
图25 裂纹尖端CODFig.25 COD of crack tip
Olsson等[93]采用拉伸加载SEN试样获得Ⅰ型裂纹快速扩展,如图26(a)所示。作者采用数值与实验相结合的方法,将载荷与裂纹长度作为边界条件,计算临界J积分JIC作为动态起裂韧性,但是该方法的缺点是JIC与初始裂纹长度相关。Sohn和Hu[94-95]采用摆锤冲击加载SEN试样,如图26(b)所示,加载方式为三点弯曲,采用式(48)计算平均层间断裂韧性。
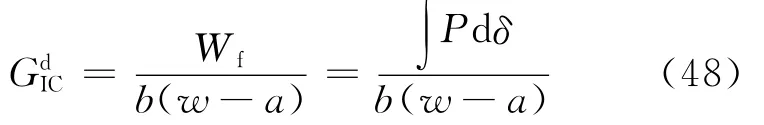
式中:w为试样的长度;Wf为外力做功;P为冲击载荷;δ为冲击加载位移。

图26 SEN试样Fig.26 SEN specimen
Ⅰ型动态层间起裂韧性主要通过DCB试样动态加载得到,计算断裂韧性时不仅需要对裂纹长度进行修正,同时需要考虑动能的变化对层间断裂韧性的影响,不同的裂纹扩展方式动能的影响不同。利用对称弯曲加载方式也是获得Ⅰ型层间起裂韧性的常用试验方法。对于这种试验方法可以通过解析法、实验法以及数值方法计算层间断裂韧性。Liu等[96]利用落锤三点弯曲加载SEN试样产生Ⅰ型动态层间断裂,测量层间断裂韧性时采用CGS方法,具体方法在本文的第3节介绍。
2.2 Ⅱ型动态层间起裂韧性的实验方法
测量Ⅱ型动态层间断裂常采用ENF和ELS试样,这两种方法简便易行,且计算层间断裂韧性简单。根据其加载形式的不同分为:①高速试验机加载;②落锤加载;③霍普金森杆加载。
Blackman等[61,97]采用高速试验机加载ENF,获得Ⅱ型动态层间断裂。实验中作者采用高速相机记录试样变形,用于确定起裂时间与加载位移。试样的动能较小,可以忽略不计;实验中由于应力波传播等原因,得到的载荷信号不准确,因此弹性模量和临界加载位移计算层间断裂韧性的公式为
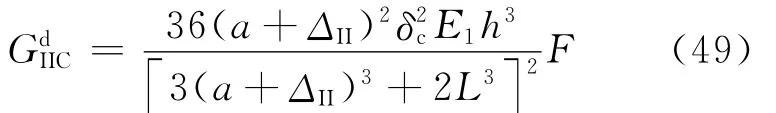
式中:F为大位移修正系数;δc为利用高速相机得到的起裂时的载荷线位移。
Todo等[98-100]采用落锤加载ENF试样,如图27所示[99],作者采用位置敏感检测器(Position Sensitive Detecor,PSD)测量ENF的弯曲挠度;裂纹尖端贴应变片,用于测量起裂时间;为了减小振动,采用橡胶垫片缓冲。作者研究发现,载荷最大值时刻并不是裂纹起裂的时间点,因此不能采用载荷最大值计算层间断裂韧性。作者采用ENF的挠曲位移和起裂时间确定层间断裂韧性。
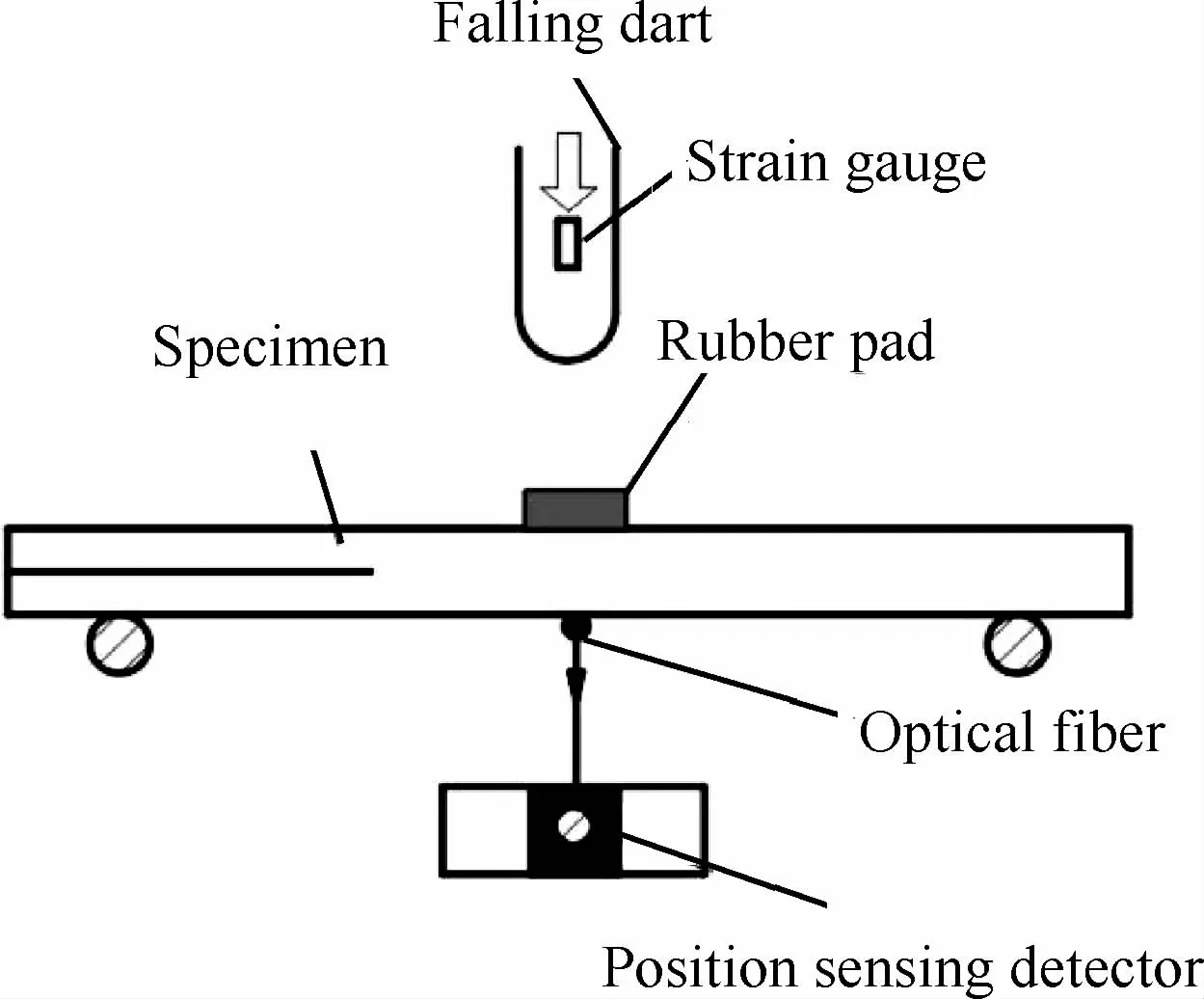
图27 动态ENF实验冲击测量系统[99]Fig.27 Impact testing system used for dynamic ENF tests[99]
Blackman[97]和Colin[101]等采用ELS试样测量动态层间断裂韧性,与ENF类似,不考虑试样的动能影响,采用弯曲挠度和材料弹性模量计算层间断裂韧性[97]:
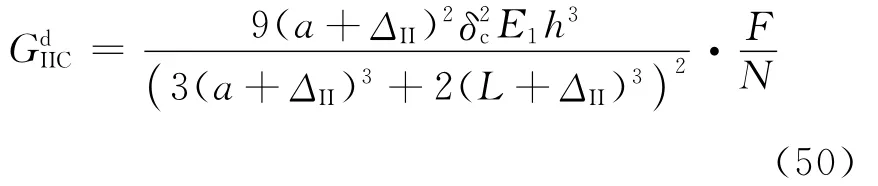
式中:L为试样的长度。(分段)动态层间断裂韧性测量与静态层间断裂不同之处在于:①起裂时间;②载荷准确度。因此在进行动态层间断裂测量时,需要解决这两个问题。HPB作为动态加载常用的仪器,利用应力波技术加载,根据应力波的传播可以计算出加载位移和加载载荷[102],因此很好地解决了动态加载过程中的难题。HPB加载ENF等试样成为测量Ⅱ型动态断裂韧性常用的方法[72,103-106],动态加载的速度最大可达20 m/s[72]。
HPB加载ENF试样分为以下3种形式:两根透射杆,如图28所示;单根透射杆,如图29所示;以及试样固定支撑,如图30所示。

图28 三杆HPB装置及ENF试样Fig.28 Three-bar HPB apparatus and ENF specimen

图29 两杆HPB装置及ENF试样Fig.29 Two-bar HPB apparatus and ENF specimen
Kusaka等[50,72,107]采用两根透射杆形式的HPB装置加载ENF试样,利用该方法可以得到入射杆端和透射杆端的载荷为
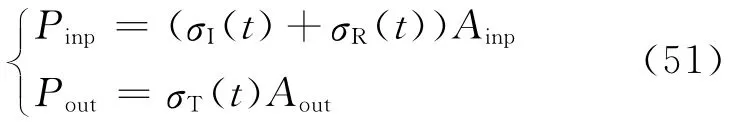
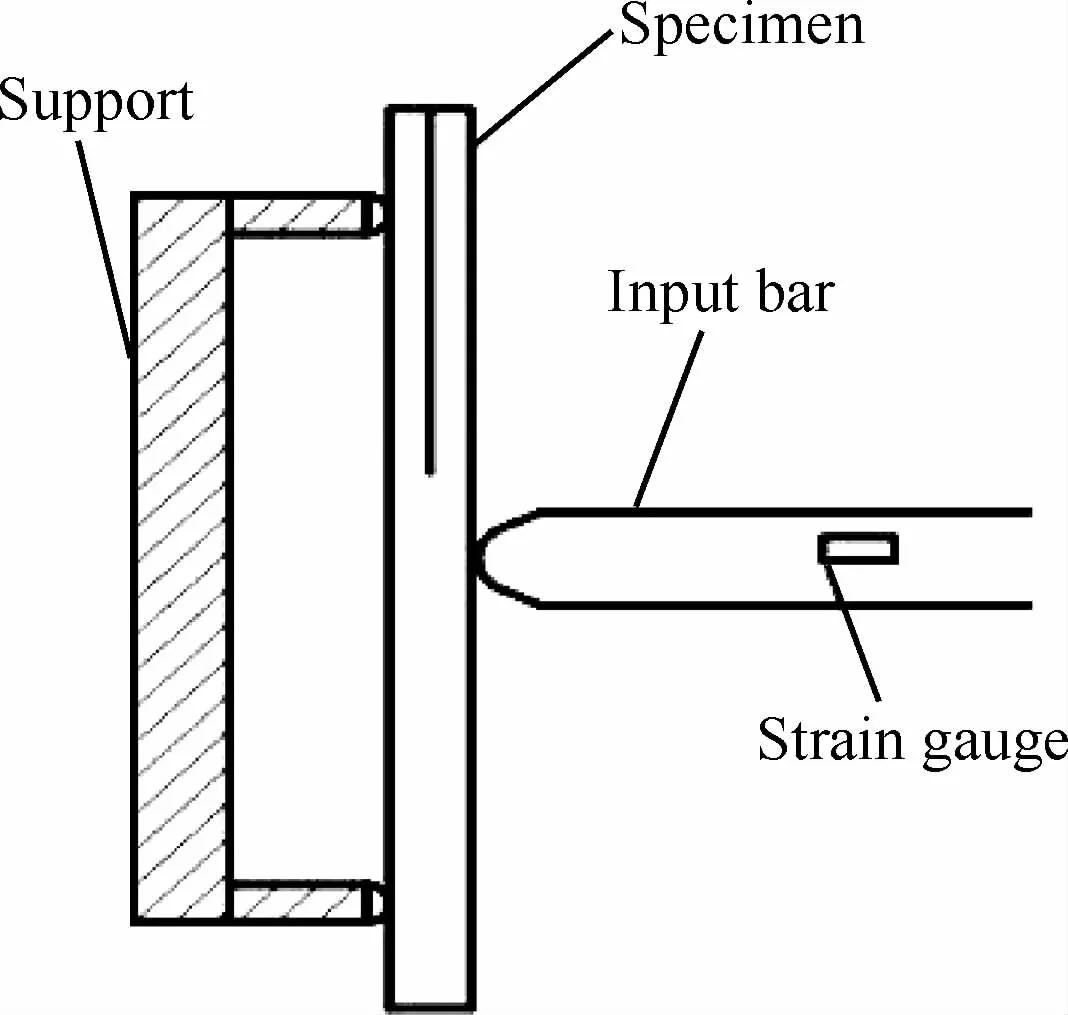
图30 单杆HPB装置及ENF试样Fig.30 One-bar HPB apparatus and ENF specimen
式中:Pinp为试样入射杆端载荷;Pout为试样透射杆端载荷;Ainp为入射杆的横截面积;Aout为透射杆的横截面积;σI(t)为入射波信号;σR(t)为反射波信号;σT(t)透射波信号。入射杆和透射杆的速度分别为
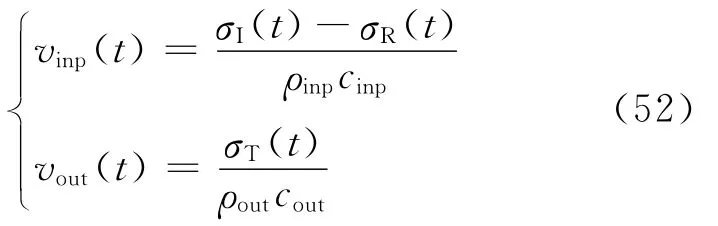
式中:vinp为入射杆杆端的速度;vout为透射杆端的速度;ρinp为入射杆的密度;ρout为透射杆的密度;cinp为入射杆波速;cout为透射杆波速。试样的挠曲变形为

Adachi等[106]同样采用的是三杆形式的HPB装置加载ENF试样,但是作者采用解析法与实验相结合的方法进行数据处理。在实验中得到入射杆端载荷信号以及透射杆端载荷信号,利用边界条件和连续性条件求解ENF的位移场;在得到位移场之后通过求解如图31所示的Γ区域(x1和x2为边界)的J积分计算层间断裂韧性:
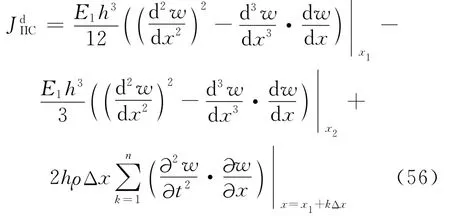
式中:E1为拉伸模量;w为ENF的挠度变形;Δx为积分步长。
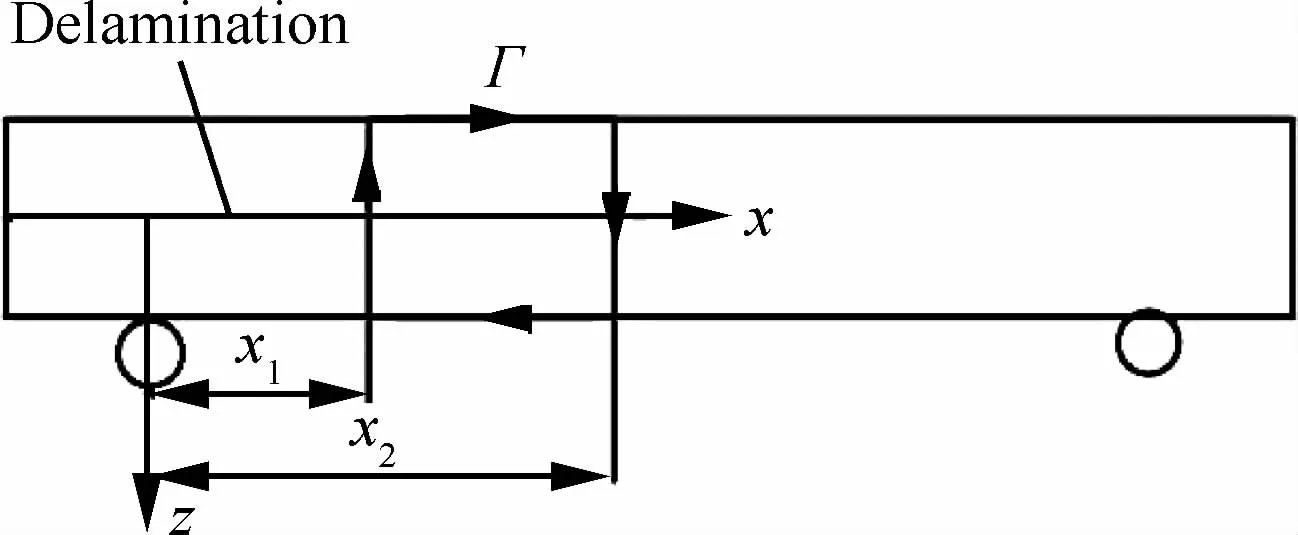
图31 J积分ENF计算区域Fig.31 ENF computational domain for J integral
Lu等[103-104,108]对两杆HPB装置加载ENF试样作了大量研究,作者对比使用压电薄膜测得的ENF试样接触点的载荷信号与应变片测得的入射杆和透射杆上的载荷信号,发现夹具对应力波的传播影响明显:透射杆上得到的载荷其幅值和波形与试样真实受力的幅值和波形均不一致。
Wiegand等[109]将试样的支撑固定,利用高速相机记录裂纹扩展,采用入射杆信号计算载荷,通过式(48)计算层间断裂韧性。
Lambros[110]和Wu[92]等采用对SEN试样裂纹面进行动态剪切冲击的方法得到II型层间断裂,如图32所示。Wu和Dzenis[92]计算Ⅱ型层间断裂韧性的方法与其计算Ⅰ型层间断裂韧性的方法相同,同样对应于图25所示的裂纹尖端,即θ=π时,第i点的Ⅱ型滑开位移uxi表示为
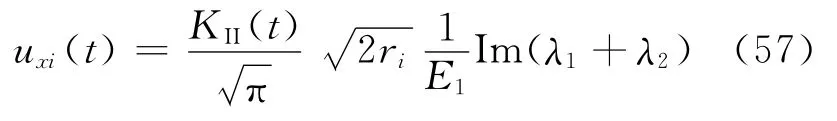
式中:KII为需要计算的应力强度因子;ri为i点至裂尖的距离。Ⅱ型断裂下,第i点y方向的张开位移uyi为0。而Lambros和Rosakis[110]采用CGS方法测量动态Ⅱ型层间断裂韧性。
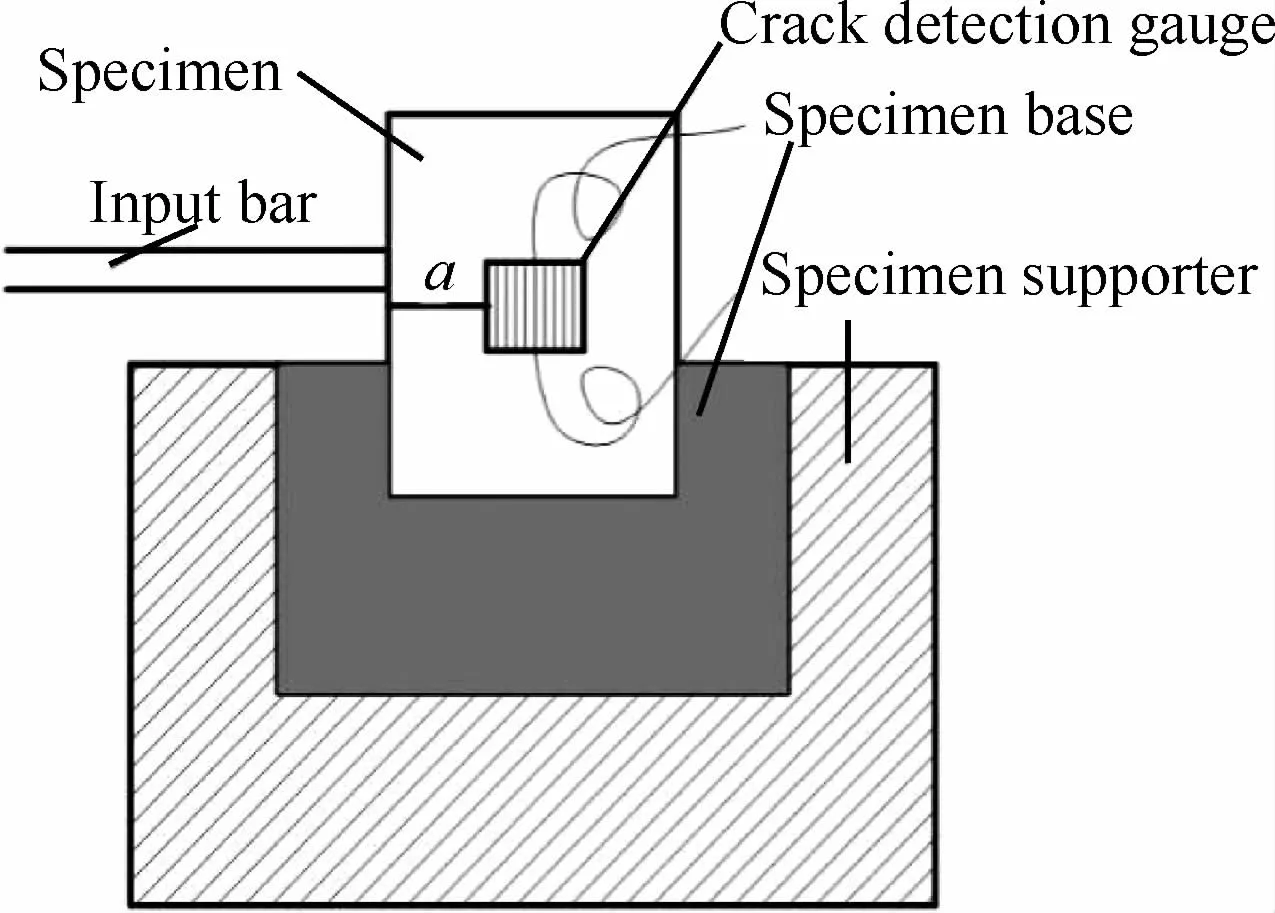
图32 SEN试样的冲击加载实验[92]Fig.32 Impact loading experiment with SEN specimen[92]
Caimmi等[111]采用落锤加载压缩单边缺口剪切(Compact Edge Notch Shear,CENS)试样获得Ⅱ型裂纹动态扩展,如图33所示。作者首先通过有限元分析夹具厚度和初始裂纹的长度对裂纹断裂混合度的影响,发现夹具厚度为20 mm,初始裂纹长度满足a/L>0.55时,断裂类型近似为纯Ⅱ型。在实验阶段,作者首先标定了夹具以及试验机的柔度,实验过程中记录载荷数据以及起裂时间,通过Irwin-Kies公式计算层间断裂韧性。作者还分析了裂纹在未扩展时裂纹尖端附近Ⅰ型和Ⅱ型J积分随时间的变化趋势。该方法得到的层间断裂韧性与ENF得到的断裂韧性有一定的差异。
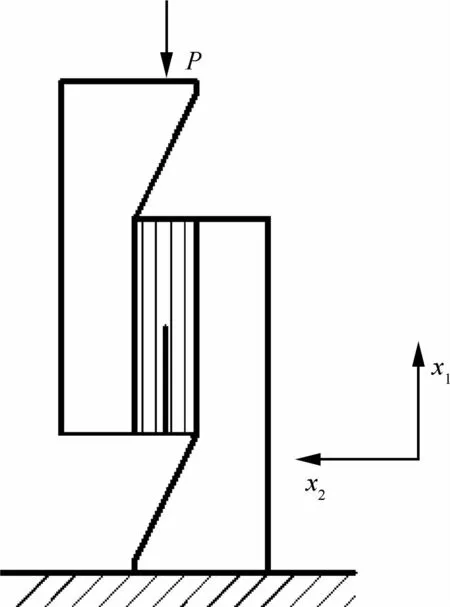
图33 CENS试样[111]Fig.33 CENS specimen[111]
Guimard等[112]通过对CLS施加上下面的位移约束,并施加固定支撑的边界条件U=0,进行Ⅱ型层间断裂实验,如图34所示。虽然该方法产生的是近似II型层间断裂,但是该方法的优点是适合于高速加载。
Sohn和Hu[95]采用摆锤冲击如图35所示的试样,得到平均的Ⅱ型层间断裂韧性。
测量Ⅱ型动态层间断裂的方法相对较少,大部分采用ENF和ELS试样。采用这两种实验形式时,一般通过起裂时间、弯曲挠度、应变片测量值以及材料的弹性模量等确定层间断裂韧性。利用其他方法测量Ⅱ型动态层间起裂韧性时,一般需要有限元方法的辅助,且需要确定裂纹是否为纯II型断裂。
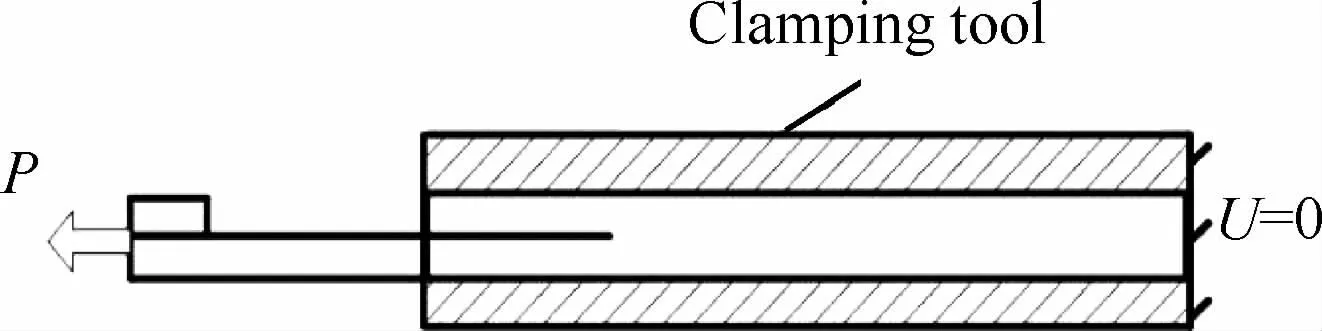
图34 改进的CLS试样Fig.34 Modified CLS specimen
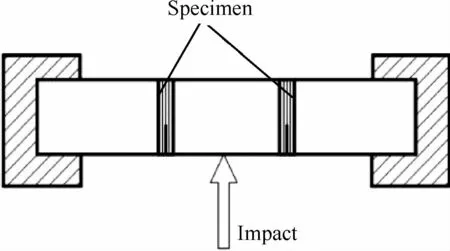
图35 剪切加载的动态Ⅱ型层间断裂实验示意图[95]Fig.35 Schematic diagram of dynamic test of ModeⅡwith shear loading[95]
2.3 Ⅰ/Ⅱ型动态层间起裂韧性的实验方法
动态Ⅰ/Ⅱ复合型层间断裂的实验方法与准静态的实验方法基本一致。动态实验中,常采用的方法为SLB和FRMM,加载仪器采用高速试验机、落锤试验机以及HPB装置。
Blackman等[61]采用高速试验机对FRMM进行加载,忽略动能的影响即
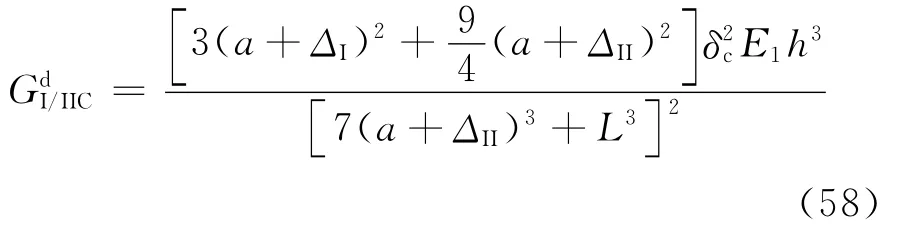
式中:L为半跨度;h为臂厚度。Todo等[99]采用落锤冲击SLB试样,实验装置如图27所示,计算层间断裂韧性的方法为
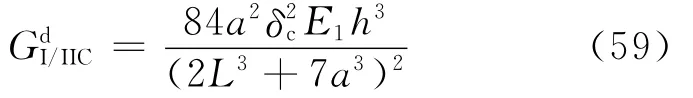
式中:L为试样跨度。但在研究时没有考虑裂纹长度的修正。
Kusaka等[73]采用含两根透射杆HPB装置加载SLB试样测量复合动态层间断裂韧性,同时在试样上粘贴应变片,计算公式与式(55)类似:
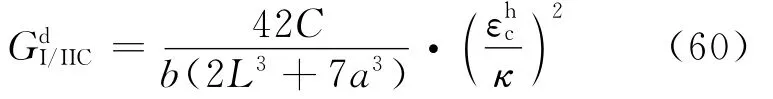
式中:κ为依赖于试样厚度、截面惯性矩和弹性模量的参量,εhc为起裂时应变片的值;C为柔度。
Govender等[113]利用改进的HPB装置对SLB试样进行撞击,如图36所示,根据光学测量装置以及应力波传播得到试样的挠曲变形和载荷为
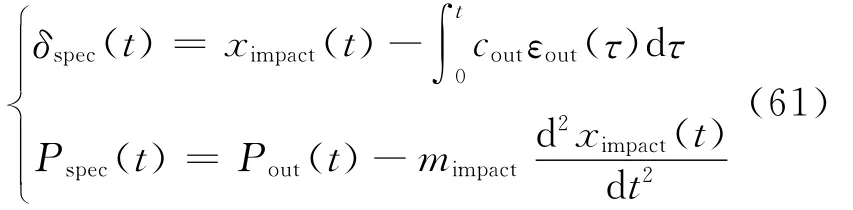
式中:ximpact为撞击杆的位移;mimpact为撞击杆的质量;cout为透射杆波速;εout为透射杆信号;Pout为透射杆的载荷。作者实验中得到δspec-Pspec的关系,然后利用准静态层间断裂韧性进行动态加载的有限元模拟,并将两者进行对比。

图36 改进的HPB实验装置[113]Fig.36 Modified HPB experiment apparatus[113]
Sohn和Hu[95]采用摆锤冲击如图37所示的试样,得Ⅰ/Ⅱ复合型层间断裂,同Ⅰ型层间断裂测试一样,采用式(48)计算平均临界能量释放率。
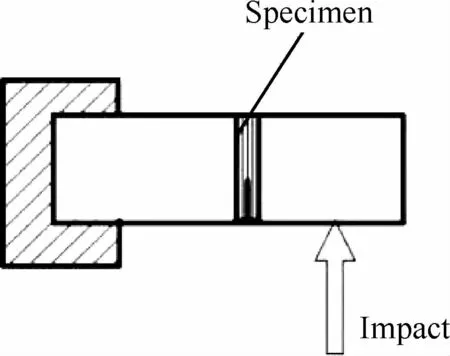
图37 动态非对称弯曲加载实验[95]Fig.37 Dynamic load experiment with asymmetric bending[95]
Liu等[34]为研究动态加载下复合型层间断裂,利用落锤冲击加载巴西圆盘试样,实验中记录载荷以及起裂时间,利用式(33)计算动态临界应力强度因子。
Ⅰ/Ⅱ复合型动态层间断裂韧性的测量方法相对较少,主要为SLB试样的动态加载,该方法所能实现的混合度单一。巴西圆盘试样能到不同混合度的层间断裂,但试样的加工复杂。除此之外,还可采用高速试验机加载ADCB试样获得动态复合型断裂。
2.4 层间裂纹动态扩展问题的研究
在裂纹的动态扩展时,裂纹扩展速度影响应力强度因子与能量释放率的关系[55]:
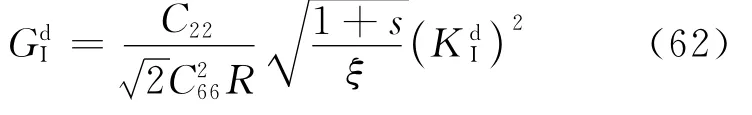
式中:Cij为材料常数;R为瑞利波方程;s为与裂纹速度相关的无量纲量;ξ为裂纹扩展速度相关的函数。Sun和Han[55]研究表明当裂纹的扩展速度小于70%的瑞利波波速时,能量释放率与应力强度因子之间的关系可以不考虑裂纹速度的影响。
相对于动态起裂韧性的测量,研究裂纹动态扩展的实验方法相对单一:在层间裂纹尖端布置黏性胶膜,储存能量,准静态加载至裂纹的动态扩展,同时测量裂纹的长度。Guo和Sun[76]以及Tsai等[114]分别研究了动态Ⅰ型、Ⅱ型以及Ⅰ/Ⅱ复合型动态裂纹扩展问题。
Guo和Sun[76]采用DCB实验研究Ⅰ层间裂纹的动态扩展问题,通过在裂纹尖端布置了一条胶黏薄膜贮存能量,以实现裂纹的快速扩展,如图38所示。Tsai等[114]在ENF试样的裂纹尖端布置黏性薄膜,以及在ADCB裂纹尖端布置黏性薄膜与加载钉,采用三点弯曲加载获得Ⅱ型和Ⅰ/Ⅱ 复合型层间裂纹的动态扩展。
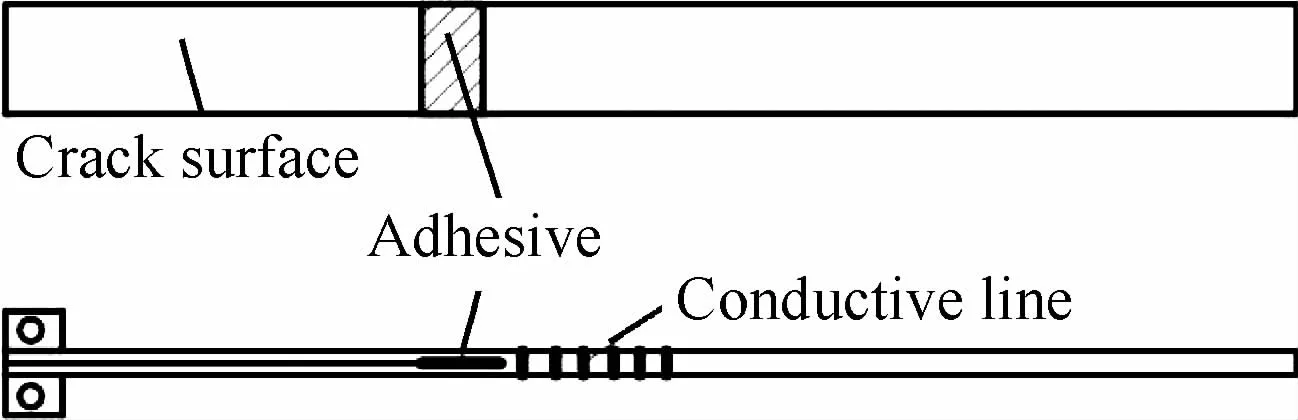
图38 裂纹尖端含有胶黏带的DCB试样[76]Fig.38 DCB specimen with adhesive tape near crack tip[76]
采用的数据处理方法有MCC方法以及能量法。能量法是通过计算裂纹扩展前后试样的应变能和动能的变化得到临界能量释放率,即

式中:ΔALLSE为应变能变化;ΔALLKE为动能变化。
2.5 小 结
测量动态层间起裂韧性所采用的试样类型与静态相似,但是动态断裂实验需要考虑更多的因素:
1)试样的动能,由于动态加载时一般采用的加载速率较大,计算整个试样能量改变时,需要考虑动能的变化。在某些情况下,动能的影响可以忽略不计。
2)载荷的测量,在动态加载下,由于振动以及应力波的传播等因素,得到的载荷信号的波动很大,不能用于层间断裂韧性的计算,为了得到准确的断裂性能,可以通过测量挠曲变形方法代替载荷,这种方法需要已知材料的弹性常数。
3)起裂时间,动态加载下起裂时间与载荷的极值不再一致,由于加载率高,加载时间很短,起裂时间稍有误差会导致测量的结果不正确。
为了得到准确的动态层间起裂韧性,可以采用数值、实验以及解析相结合的方法。
对动态裂纹的扩展问题研究较少,且研究方法单一,研究结果发现,裂纹扩展速度对断裂韧性的影响较小。
3 光学测量技术在层间断裂力学中的应用
随着数字图像技术的发展,光学测量技术被广泛地应用于固体力学实验研究领域,特别是在断裂力学的测量中[115]。光学测量技术通常可以提供全场的位移分布,而断裂韧性往往需要通过裂纹尖端的位移场反推得到。在进行层间断裂韧性测量时最常用的两种光学测量方法为数字图像相关(DIC)技术和CGS干涉测量技术。
3.1 DIC技术在层间断裂韧性测量中的应用
数字图像相关技术的主要思想是通过对变形前的参考图像和变形后的图像进行相关计算得到物体表面的全场位移和应变。
DIC技术在层间断裂韧性测量中存在很多的应用形式,其中最直接的方法是提取DIC计算位移,Upadhyaya等[116]通过DIC技术提取DCB试样加载点的位移计算试样加载点转角θ,通过式(64)计算临界J积分[117-118]:

式中:b为试样的厚度;θc为起裂时加载点的转角。
Xavier等[119-121]利用DIC得到的位移场计算Ⅰ型和Ⅱ型层间裂纹尖端张开位移,根据梁理论计算出断裂韧性,通过式(65)确定拉伸分离曲线(Traction Separation Law,TSL):
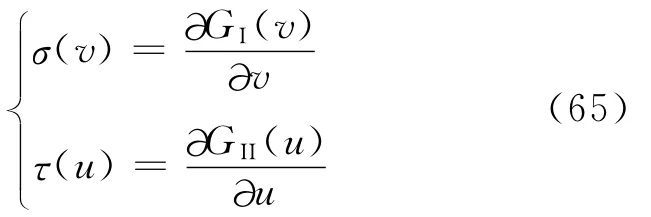
式中:v为裂纹尖端的张开位移;u为裂纹尖端的剪切位移。
Dubois等[122-123]利用有限元技术和DIC技术计算当材料的基本力学性能未知时的层间断裂韧性,使用的方法为基于DIC和FEM平行计算的方法,如图39所示,F为进行FEM计算时的载荷状态,σ为裂纹尖端的应力状态。利用DIC技术得到试样的位移场,计算出临界相对位移因子Kα(ε);有限元方法中选取不同的材料类型,采用与试验完全一致的载荷边界F,计算临界应力强度因子Kα(σ),其中临界相对位移因子和临界应力强度因子的关系为

式中:Cα为缩减的弹性常数。利用式(67)即可计算层间断裂韧性:
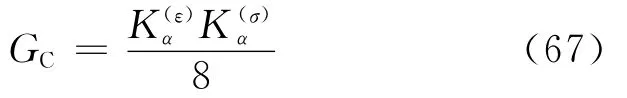
Lee等[124-125]利用SEN试样以及DIC技术测量层间断裂的应力强度因子,如图40所示,试样的长度为L,宽度为W,纤维方向为β,对于裂纹尖端的任意一点(r,θ),其x方向和y方向的位移的解析解可表示为
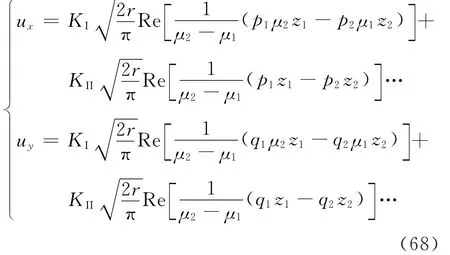
式中:ux、uy为x、y方向的位移;r为距裂纹尖端的距离;μ1和μ2为式(69)虚部为正的两个根,其表达式为
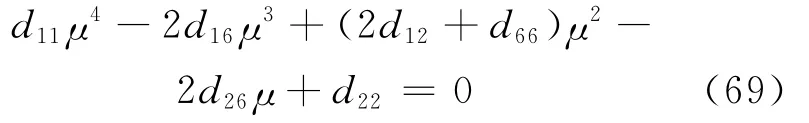
式中:dij为各向异性材料的柔度矩阵的分量。pj、qj以及zj可表示为

式中:θ为如图40所示的转角。利用DIC技术同样可以得到裂纹尖端的位移场,对DIC计算的位移场与解析的裂尖位移场进行最小二乘法拟合即可得出应力强度因子。

图39 基于DIC和FEM方法的平行计算方法[122]Fig.39 Parallel computing approaches based on DIC and FEM method[122]
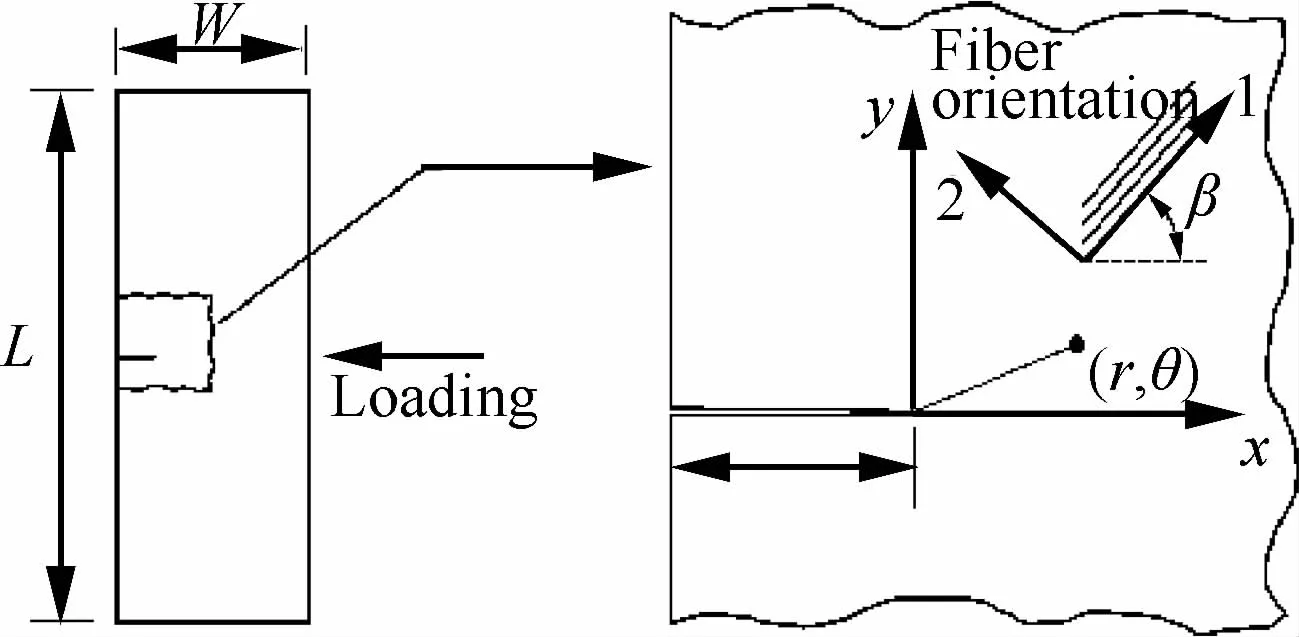
图40 裂纹尖端位移场[125]Fig.40 Crack-tip displacement field[125]
Mathieu等[65]利用DIC技术确定裂纹尖端的位置xc。具体方法如下:①利用DIC技术得到感兴趣区域(Region of Interest,ROI)的位移场umeas;②建立ROI区域的有限元模型,ROI周边节点的位移作为位移边界条件,假设裂纹尖端的位置为xc,计算位移分布为ucomp;③改变有限元中裂纹尖端的位置xc,利用式(71)最小化得到真实的裂纹尖端位置:
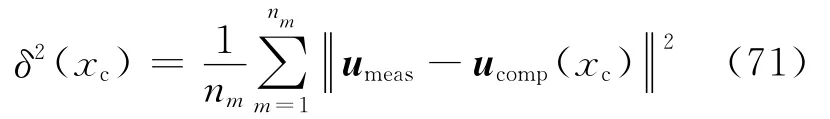
式中:nm为DIC计算得到的位移点的个数。Blaysat等[126]结合全局DIC技术计算内聚力单元的TSL。
DIC技术适用于任何形式的实验方法,它可以得到试样表面的位移场。DIC技术与解析方法和有限元分析方法相结合使用即可用于层间断裂的测量中。
3.2 CGS技术
相干梯度敏感干涉测量技术的基本原理是[127]:通过光学干涉建立面内应力梯度或离面位移梯度与光线微小偏转量之间的关系,利用两个平行光栅重组,使由试件变形导致的扭曲光束产生干涉条纹。该方法分为透射和反射两种情况,透射用于研究透明体的局部变形,最终得到面内应力梯度场;反射用于研究非透明物体的变形,得到离面位移梯度场。
Liu等[96,128]利用反射CGS干涉测量技术对三点弯曲SEN试样的Ⅰ型动态层间断裂进行了研究,如图41所示,试样的长度为2l,宽度为b,厚度为h,受冲击载荷P(t)的作用。Lambros和Rosakis[110]利用该技术研究了Ⅱ型动态层间断裂。反射CGS相干测量技术的基本方程[128]为
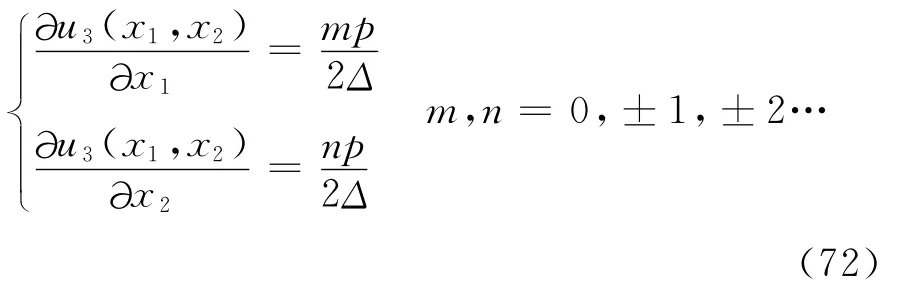
式中:u3为离面位移;p为光栅截距;Δ为两平行光栅的间距。m和n代表不同的条纹级数。对于各向异性材料:
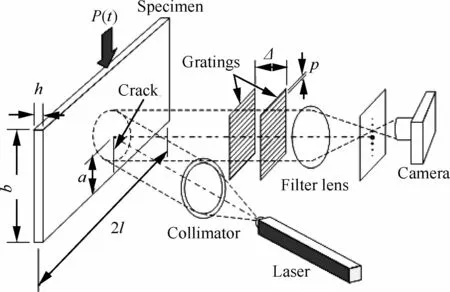
图41 CGS实验装置与SEN试样[128]Fig.41 CGS experiment setup and SEN specimen[128]
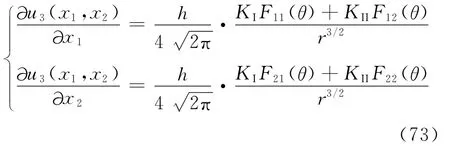
式中:h为试样的厚度;Fij(θ)为与材料参数和角度θ相关的函数。结合式(72)和式(73):

从式(74)可以看出只要知道条纹图中任意一点的条纹级数,即可求出应力强度因子。
3.3 小 结
本节介绍了两种用于层间断裂实验的光学测量方法。DIC技术用于层间断裂的测量有多种使用形式,包括直接使用和间接使用。DIC技术可以提供的位移信息多,可以直接利用DIC计算的位移场以及解析解获得应力强度因子;也可以结合使用FEM,计算裂纹尖端的位置或计算能量释放率。CGS干涉测量技术的用法相对单一,因此主要讲述了CGS的测试原理。
4 加载速率对层间断裂韧性的影响
本节的主要目的是对文献中加载速率对Ⅰ型、Ⅱ型以及Ⅰ/Ⅱ复合型层间起裂韧性的影响进行综述。
4.1 加载速率对Ⅰ型层间断裂韧性的影响
Aliyu等[80]利用DCB试样研究了应变率对AS4/3501-6碳纤维/环氧树脂复合材料断裂韧性的影响。在高速情况下,利用置于裂纹尖端的应变片,或裂尖前方导电的回路监测裂纹的扩展。结果发现,加载速率为8.5 mm/s时的断裂韧性比准静态的断裂韧性高出28%,即加载速率的增加使得层间断裂韧性增加。Daniel等[79]利用DCB以及HTDCB试样研究了两种碳纤维复合材料的层间断裂韧性,其中一种为脆性基体材料AS4/3501-6,另一种为弹性体改性的韧性基体材料T300/F-185。作者发现对于脆性基体材料,Ⅰ型层间断裂韧性随加载速率呈现增加先上升后下降的趋势,断裂韧性最大值比准静态下的断裂韧性高出46%;而对于韧性基体,层间断裂韧性随加载速率的增加逐渐减小。碳纤维/环氧树脂层间断裂韧性的率相关性与基体材料密切相关。
Hashemi等[48]研究了碳纤维/聚醚醚酮(PEEK)复合材料层间断裂韧性的率相关性,加载点位移速率范围为0.2~20 mm/min,发现Ⅰ型层间断裂韧性是率无关的。
Gillespie等[129-130]研究了加载速率范围在0.25~250 mm/min之间时,碳纤维/环氧树脂以及碳纤维/PEEK复合材料的Ⅰ型层间断裂韧性的率相关性。对于碳纤维/环氧树脂复合材料其层间断裂韧性是率无关的,碳纤维/PEEK复合材料的Ⅰ型层间断裂韧性随加载速率的增加,先增加后降低。实验中PEEK复合材料的载荷位移曲线呈现明显的非线性,因此作者提出基体塑性、黏弹性以及微裂纹聚合等因素导致其率相关性:在低速下,层间材料表现为韧性断裂,随着加载速率的增加,层间断裂的过程区随之增大,导致断裂韧性的增加;而当加载速率达到一定程度时,材料则表现为脆性断裂,正是由于这种断裂类型的转变,使得碳纤维/PEEK的Ⅰ型层间断裂韧性呈现出率的负相关性。
Blackman等[74,90]也研究了碳纤维/环氧树脂和碳纤维/PEEK复合材料断裂韧性的率相关性,其最大加载速率为15 m/s,发现随着加载速率的增加,碳纤维/环氧树脂复合材料的层间断裂韧性不随加载速率改变,而碳纤维/PEEK复合材料断裂韧性随加载速率的增加减少了20%。
Smiley和Pipes[75]研究了碳纤维/环氧树脂和碳纤维/PEEK复合材料断裂韧性的率相关性,加载速率从4.2×10-6m/s到6.7×10-1m/s,发现碳纤维/PEEK的断裂韧性从1.5 kJ/m2降低至0.35 kJ/m2,而碳纤维/环氧树脂的断裂韧性从0.18 kJ/m2降低至0.04 kJ/m2。作者分析这是由基体材料的率相关性导致的。
Kusaka等[50-51,73]为研究碳纤维/环氧树脂断裂韧性的率相关性,采用两种试样和加载装置,在静态下,采用试验机加载DCB试样,在动态下,采用霍普金森压杆(SHPB)加载楔形插入断裂WIF试样。研究发现,复合材料的层间断裂韧性与加载速率存在阶梯型的相关性,在低速和高速下,断裂韧性是率无关的,在中速率加载区域,断裂韧性随加载速率的增加逐渐减小。Kusaka等[73]还研究了基体材料断裂韧性的率相关性,发现在低速下,复合材料的断裂韧性低于基体材料断裂韧性,而在高速下,两者的值相近,分析原因为在两种状态下断裂机制不同导致的:在低速下,主要由于纤维与基体间的脱胶导致分层,而在高速下,由于基体材料的断裂导致分层破坏。
You和Yum[131]研究了在不同加载速率下碳纤维/环氧树脂的层间断裂韧性的变化规律,发现在低加载速率下,层间断裂韧性几乎不变,当速率增加至200 mm/s时,层间断裂韧性增加了73%。
Mall等[132]在研究碳纤维/PEEK复合材料时,发现在0.05~100 cm/min加载速率范围内,Ⅰ型断裂韧性降低了65%,作者分析是由于在高速加载下,塑性变形区变小导致的。Fracasso等[133]研究了层间增韧碳纤维/PEEK与编织碳纤维/PEEK复合材料Ⅰ型层间断裂韧性与加载速率间的关系,对于两种材料随着裂纹速度的增加断裂韧性均减小。
Hug等[78]通过改进加载装置,实现了最高20 m/s的加载速度,同时保证对称加载,利用DCB试样对T300/914碳纤维/环氧树脂复合材料的I型层间断裂韧性进行研究,发现在该速度范围内,裂尖的张开速率为0.004~1.6 m/s,断裂韧性率无关,结果与Kusaka等[50]的结果一致。
Sun和Han[55]利用有限元方法和实验相结合的方法研究I型层间断裂的率相关性,发现在层间断裂韧性为率无关的。
许多学者也研究了胶接层断裂韧性随加载速率的变化规律。Sun等[86,134-135]研究了胶接层Ⅰ型层间断裂韧性的率相关性,分别采用了3种加载方式:在低速下,采用DCB试样,在中速下,采用位移控制的楔入加载DCB试样,在高速下,采用动态撞击楔入加载试样。结果发现,裂纹的准静态生长是率无关的,在很高的速度下,仍可能发生裂纹的准静态生长;随着裂纹速度的增大,裂纹变为动态断裂,但是其能量释放率没有太大的变化。Carlberger等[136]研究了结构环氧胶黏剂,受温度和加载速率的影响,发现Ⅰ型层间断裂韧性呈现正率相关性。最近,Blackman等[61]系统地研究了两种胶黏剂与4种不同类型复合材料组成的DCB试样的I型层间断裂韧性与加载速率的关系,加载速率最高达15 m/s,发现对于所有的胶黏剂材料其I型层间断裂韧性均呈现负的率相关性。May等[137]利用TDCB试样研究了加载速率对胶黏剂层间断裂的影响,发现层间断裂韧性随加载速率的增加而增大,且呈现出双线性增长形式。
研究结果有时是相互矛盾的,例如,对于同种材料AS4/3501-6碳纤维/环氧树脂复合材料的层间断裂韧性率相关性,Aliyu等[80]和Smiley等[75]得到的结果完全不一致:Aliyu等认为层间断裂韧性为正率相关性,Smiley等认为是负率相关性。
4.2 加载速率对Ⅱ型层间断裂韧性的影响
Smiley和Pipes[138]利用ENF试样研究了碳纤维/PEEK和碳纤维/环氧树脂复合材料Ⅱ型层间断裂性的率相关性,随着加载速率的增加,基体复合材料的层间断裂韧性由1 kJ/m2减小至0.4 kJ/m2,环氧树脂基体复合材料的断裂韧性由0.46 kJ/m2减小至0.06 kJ/m2。PEEK是典型的热塑性材料,热塑性复合材料的Ⅱ型层间断裂韧性的率敏感性由材料断裂类型的转变造成:在低速下,基体表现为韧性断裂;而在高速下,基体断裂则转变为脆性断裂。
Kageyama和Kimpara[139]研究了碳纤维/环氧树脂复合材料Ⅱ型层间断裂韧性的率相关性,最大的加载速率为8 m/s,结果发现Ⅱ型层间断裂韧性呈现正率相关性,在最大加载速率下,断裂韧性增大至准静态测量值的1.8倍。
Kusaka等[72-73,140]利用SHPB加载ENF试样研究两种了碳纤维/环氧树脂复合材料(T300/2500和IM600/133)Ⅱ型层间断裂韧性的率相关性,其中T300/2500为脆性基体复合材料,IM600/133为基体增韧的复合材料,加载速率范围为10-7~20 m/s。结果发现,断裂韧性首先随加载速率增加而增大,然后随加载速率的增加降低,即断裂韧性存在极值,T300/2500的动态断裂韧性比极值降低13%,IM600/133的动态断裂韧性要比极值小29%,即高含韧性基体的复合材料对加载速率更加敏感。分析原因是在低速情况下,纤维与基体界面脱胶是主要的断裂机制;在高速下,基体材料的断裂为主要的断裂机制。通过微观观察,在高低速下基体材料变形区域的大小不同,在高速下基体材料变形区域更小。
Berger和Cantwell[141]研究了碳纤维/酚醛塑料与碳纤维/PEEK两种复合材料Ⅱ型层间断裂韧性与加载速率和温度的相关性。在低温下,碳纤维/酚醛塑料呈现负率相关性,在接近酚醛塑料玻璃转变温度时,Ⅱ型层间断裂韧性随加载速率增加而增大。碳纤维/PEEK的Ⅱ型层间断裂韧性随加载速率的增加而增大,增加约25%。这种率相关性与基体材料的屈服强度有关,小应变率下材料的屈服强度较低,导致层间断裂韧性较小。
Cantwell[142]研究发现在0.01 mm/min~3 m/s加载速率范围内碳纤维/PEEK复合材料Ⅱ型层间断裂韧性呈现正率相关性。
Maikuma等[143]利用中心裂纹三点弯曲试样研究了碳纤维/PEEK与碳纤维/环氧树脂复合材料Ⅱ型层间断裂韧性的率相关性,结果发现两种材料的动态起始断裂韧性分别降低20%和28%。分析原因是在高速下,材料的塑性变形和撕裂破坏较少导致的。
Blackman等[144]延续Ⅰ型层间断裂的工作,通过使用ELS试样对碳纤维/环氧树脂和碳纤维/PEEK复合材料Ⅱ型层间断裂韧性的率相关性进行了研究,发现两种材料在所研究的加载速率范围内是率无关的。
Todo等[98]研究了碳纤维/PA-6和玻璃纤维/PA-6两种材料的率相关性,碳纤维/PA-6的断裂韧性随加载速率增大而增加53%,而玻璃纤维/PA-6随加载速率增大而降低34%。产生这种现象的原因是玻璃纤维/PA-6的层间破坏主要由PA-6基体破坏导致,而碳纤维/PA-6的破坏由基体与纤维间的界面层控制,且玻璃纤维/PA-6的断裂韧性要大于碳纤维/PA-6的断裂韧性。
Compston等[145]研究了在1 mm/min~3 m/s的加载速率之间,玻璃纤维增强的两种基体复合材料的层间断裂韧性的率相关性,一种基体为脆性乙烯基塑料酯,另一种为经过橡胶改性的韧性乙烯基塑料酯,结果发现Ⅱ型层间断裂韧性无明显的率相关性。在不同加载速率下,Ⅱ型层间断裂面上均出现大量的光滑纤维,即断裂是由界面脱胶导致的,微观观察与宏观力学行为相吻合。
Jiang等[146]研究了碳纤维/环氧树脂和层间增韧碳纤维/环氧树脂Ⅱ型层间断裂韧性的率相关性,发现碳纤维/环氧树脂材料为率无关的,而层间增韧复合材料的层间断裂韧性随加载速率的增大而增加。层间增韧复合材料在低速下的断裂为界面的裂纹扩展主导,在高速下为层间基体断裂主导,这种断裂类型的转变导致材料具有率相关性,而未增韧的复合材料的断裂只是由于界面脱胶造成。
同样,研究人员对胶接层Ⅱ型断裂韧性的率相关性进行了研究。Wade和Cantwell[147]研究了二氧化硅颗粒增强环氧树脂胶黏剂的断裂韧性随温度和加载速率变化的关系,发现它对两者均十分敏感:在60℃时,断裂韧性降为室温的一半,增加加载速度,可使断裂韧性增大为准静态的2.5倍。Carlberger等[136]研究发现环氧树脂胶黏剂Ⅱ型层间断裂韧性随加载速率间增加而减小。Banea等[148]研究了温度和加载速率对Ⅱ型层间断裂的影响,发现断裂韧性随温度的增加线性降低,随加载速率的增加而增加。Blackman等[61]利用ENF和ELS试样研究了胶接层的Ⅱ型层间断裂,发现其与加载速率成负相关。May等[137]利用锥形ENF试样研究了胶黏剂Ⅱ型层间断裂韧性的率相关性,发现层间断裂韧性随加载速率的增加而增加。
Ⅱ型层间断裂韧性的率相关性受多种因素的影响,例如在不同的加载速率下,可能发生基体破坏或界面破坏,断裂形式的不同会导致断裂韧性的率相关性。
4.3 加载速率对Ⅰ/Ⅱ型层间断裂韧性的影响
对于Ⅰ/Ⅱ复合型断裂韧性的率相关性的研究较少。Kusaka[73]通过使用HPB加载MMF试样研究了层间增韧的碳纤维/环氧树脂复合材料Ⅰ/Ⅱ复合断裂韧性的率相关性,结果为层间断裂韧性随加载速率的增加呈现出先增加后而降低的趋势,微观观察动态断裂面比静态断裂面平滑。Blackman等[61,97]研究了碳纤维/环氧树脂、碳纤维/PEEK复合材料以及胶接材料的复合型层间断裂韧性随加载速率的变化规律,发现复合型层间断裂韧性为率无关的。
4.4 小 结
通过对文献进行综述,调查了加载速率对层间起裂韧性影响的实验结果,给出了一些趋势性的结论以及相对应的解释。但是,层间起裂韧性的率相关性并没有一致的结论,研究的材料不同得出的结论可能不同。基本上来说,基体的率敏感性影响了复合材料层间断裂的率敏感性。基体的性质对Ⅰ型层间断裂韧性的影响较大,因为Ⅰ型层间断裂韧性由裂纹尖端塑性变形控制。Ⅱ型层间断裂由裂纹尖端塑性变形和纤维基体界面同时控制,因此基体的率敏感性往往不能明显地表现。
此外,加载速率的变化会导致断裂机制的变化,随着加载速率的增加,材料的断裂形式会由韧性断裂到脆性断裂进行转变,从而导致层间断裂韧性改变。且随着加载速率的增加,断裂部位也可能发生转变,可能的断裂部位有基体材料的断裂以及基体与纤维界面之间的断裂。
5 结 论
对准静态和动态加载下层间断裂韧性的测量技术进行综述,重点介绍了各种实验技术中断裂参数的获取。同时介绍了两种光学测量方法在层间断裂实验中的应用。最后对文献中加载速率对层间断裂韧性的影响进行了汇总。通过文献综述,可以得出的一个一般化的结论:应变率会影响基体的性质和断裂形式,导致应变率对层间断裂韧性的影响。
[1] Du S Y.Advanced composite materials and aerospace engineering[J].Acta Materiae Compositae Sinica,2007,24(1):1-12(in Chinese).杜善义.先进复合材料与航空航天[J].复合材料学报,2007,24(1):1-12.
[2] Yi X S.Theory and application of high-performance polymer matrix composites[M].Beijing:National Defense Industry Press,2011:1-20(in Chinese).益小苏.先进树脂基复合材料高性能化理论与实践[M].北京:国防工业出版社,2011:1-20.
[3] Banea M D,Da Silva L F M.Adhesively bonded joints in composite materials:an overview[J].Proceedings of the Institution of Mechanical Engineers,Part L:Journal of Materials Design and Applications,2009,223(1):1-18.
[4] Chaves F J,Da Silva L F M,De Moura M F S F,et al.Fracture mechanics tests in adhesively bonded joints:a literature review[J].The Journal of Adhesion,2014,90(12):955-992.
[5] Gozluklu B,Uyar I,Coker D.Intersonic delamination in curved thick composite laminates under quasi-static loading[J].Mechanics of Materials,2015,80(Part B):163-182.
[6] Thawre M M,Pandey K N,Dubey A,et al.Fatigue life of a carbon fiber composite T-joint under a standard fighter aircraft spectrum load sequence[J].Composite Structures,2015,127:260-266.
[7] Cui H,Li Y L,Liu Y Y,et al.Numerical simulation of composites joints based on cohesive zone model[J].Acta Materiae Compositae Sinica,2010,27(2):161-168(in Chinese).崔浩,李玉龙,刘元镛,等.基于粘聚区模型的含填充区复合材料接头失效数值模拟[J].复合材料学报,2010,27(2):161-168.
[8] Xu W,Chen L,Zhang Q C,et al.The mechanical behavior of interface adhesion and its characterization[J].Scientia Sinica Technologica,2012,42(12):1361-1376(in Chinese).许巍,陈力,张钱城,等.粘结界面力学行为及其表征[J].中国科学:技术科学,2012,42(12):1361-1376.
[9] Zhu L,Cui H,Li Y L,et al.Numerical simulation of the failure of composite T-joint with defects[J].Acta Aeronautica et Astronautica Sinica,2012,33(2):287-296(in Chinese).朱亮,崔浩,李玉龙,等.含缺陷复合材料T型接头失效数值分析[J].航空学报,2012,33(2):287-296.
[10] Shen Z,Zhang Z L,Wang J,et al.Characterization of damage resistance and damage tolarance behavior of com-posite laminats[J].Acta Materiae Compositae Sinica,2004,21(5):140-145(in Chinese).沈真,张子龙,王进,等.复合材料损伤阻抗和损伤容限的性能表征[J].复合材料学报,2004,21(5):140-145.
[11] Hutchinson J W,Suo Z.Mixed mode cracking in layered materials[J].Advances in Applied Mechanics,1991,29:63-191.
[12] Suo Z,Hutchinson J.Interface crack between two elastic layers[J].International Journal of Fracture,1990,43(1):1-18.
[13] Davies G,Zhang X.Impact damage prediction in carbon composite structures[J].International Journal of Impact Engineering,1995,16(1):149-170.
[14] Blackman B R K,Hadavinia H,Kinloch A J,et al.The use of a cohesive zone model to study the fracture of fibre composites and adhesively-bonded joints[J].International Journal of Fracture,2003,119(1):25-46.
[15] He X C.A review of finite element analysis of adhesively bonded joints[J].International Journal of Adhesion and Adhesives,2011,31(4):248-264.
[16] Davallo M.Factors affecting fracture behaviour of composite materials[J].International Journal of Chem Tech Research,2010,2(4):2125-2130.
[17] Compston P,Jar P Y B,Davies P.Matrix effect on the static and dynamic interlaminar fracture toughness of glass-fibre marine composites[J].Composites Part B:Engineering,1998,29(4):505-516.
[18] Tang Y,Ye L,Zhang Z,et al.Interlaminar fracture toughness and CAI strength of fibre-reinforced composites with nanoparticles—A review[J].Composites Science and Technology,2013,86:26-37.
[19] Cantwell W,Kausch H.Fracture behaviour of epoxy resins[C]//Chemistry and Technology of Epoxy Resins.Berlin:Springer Netherlands,1993:144-174.
[20] Frassine R,Pavan A.Viscoelastic effects on the interlaminar fracture behaviour of thermoplastic matrix composites:I.rate and temperature dependence in unidirectional PEI/carbon-fibre laminates[J].Composites Science and Technology,1995,54(2):193-200.
[21] Frassine R,Rink M,Pavan A.Viscoelastic effects on the interlaminar fracture behaviour of thermoplastic matrix composites:II.rate and temperature dependence in unidirectional PEEK/carbon-fibre laminates[J].Composites Science and Technology,1996,56(11):1253-1260.
[22] Kinloch A.Mechanics and mechanisms of fracture of thermosetting epoxy polymers[M]//Dusek K.Epoxy resins and composites I.Berlin:Springer Berlin Heidelberg,1985:45-67.
[23] Brunner A,Blackman B R K,Davies P.A status report on delamination resistance testing of polymer-matrix composites[J].Engineering Fracture Mechanics,2008,75(9):2779-2794.
[24] Reeder J R,Rews J H.Mixed-mode bending method for delamination testing[J].AIAA Journal,1990,28(7):1270-1276.
[25] Hojo M,Kageyama K,Tanaka K.Prestandardization study on mode I interlaminar fracture toughness test for CFRP in Japan[J].Composites,1995,26(4):243-255.
[26] Tanaka K,Kageyama K,Hojo M.Prestandardization study on mode II interlaminar fracture toughness test for cfrp in Japan[J].Composites,1995,26(4):257-267.
[27] ASTM International.ASTM D 5528 Standard test method for mode Iinterlaminar fracture toughness of unidirectional fiber-feinforced polymer matrix composites[S].West Conshohocken:ASTM International,2007.
[28] ASTM International.ASTM D 6671/D6671M-06 Standard test method for mixed mode I-mode II interlaminar fracture toughness of unidirectional fiber reinforced polymer matrix composites[S].West Conshohocken:ASTM International,2006.
[29] Sun C,Qian W.The use of finite extension strain energy release rates in fracture of interfacial cracks[J].International Journal of Solids and Structures,1997,34(20):2595-2609.
[30] Lin S T,Feng Z,Rowlands R E.Thermoelastic determination of stress intensity factors in orthotropic composites using the J-integral[J].Engineering Fracture Mechanics,1997,56(4):579-592.
[31] Shokrieh M,Heidari R M,Ayatollahi M.Interlaminar fracture toughness of unidirectional DCB specimens:A novel theoretical approach[J].Polymer Testing,2012,31(1):68-75.
[32] Shokrieh M,Heidari R M,Ayatollahi M.Calculation of GIfor a multidirectional composite double cantilever beam on two-parametric elastic foundation[J].Aerospace Science and Technology,2011,15(7):534-543.
[33] Huang Y,Liu C,Stout M.A Brazilian disk for measuring fracture toughness of orthotropic materials[J].Acta Materialia,1996,44(3):1223-1232.
[34] Liu C,Lovato M,Stout M,et al.Measurement of the fracture toughness of a fiber-reinforced composite using the Brazilian disk geometry[J].International Journal of Fracture,1997,87(3):241-263.
[35] Mankour A,Bachir B B,Belhouari M.Brazilian disk test simulation intended for the study of interfacial cracks in bimaterials[J].Computational Materials Science,2008,43(4):696-699.
[36] Choupani N.Experimental and numerical investigation of the mixed-mode delamination in Arcan laminated specimens[J].Materials Science and Engineering:A,2008,478(1):229-242.
[37] Cognard J Y,Créac’hcadec R,Sohier L,et al.Analysis of the nonlinear behavior of adhesives in bonded assemblies—comparison of TAST and Arcan tests[J].International Journal of Adhesion and Adhesives,2008,28(8):393-404.
[38] Cognard J Y,Sohier L,Davies P.A modified Arcan test to analyze the behavior of composites and their assemblies under out-of-plane loadings[J].Composites Part A:Applied Science and Manufacturing,2011,42(1):111-121.
[39] Greer J M,Jr,Galyon D S E,Hammond M J.Some comments on the Arcan mixed-mode(Ⅰ/Ⅱ)test specimen[J].Engineering Fracture Mechanics,2011,78(9):2088-2094.
[40] Nikbakht M,Choupani N,Hosseini S R.2D and 3D interlaminar fracture assessment under mixed-mode loading conditions[J].Materials Science and Engineering:A,2009,516(1-2):162-168.
[41] Huang Y,Wang W,Liu C,et al.Analysis of intersonic crack growth in unidirectional fiber-reinforced composites[J].Journal of the Mechanics and Physics of Solids,1999,47(9):1893-1916.
[42] Rizov V.Fracture in composites—An overview(PartⅠ)[J].Journal of Theoretical and Applied Mechanics,2012,42(2):3-42.
[43] Rizov V.Fracture in composites—An overview(PartⅡ)[J].Journal of Theoretical and Applied Mechanics,2012,42(3):23-32.
[44] de Morais A B,Rebelo C C,de Castro P,et al.Interlaminar fracture studies in Portugal:past,present and future[J].Fatigue&Fracture of Engineering Material&Structures,2004,27(9):767-773.
[45] Farmand-Ashtiani E,Cugnoni J,Botsis J.Specimen thickness dependence of large scale fiber bridging in mode I interlaminar fracture of carbon epoxy composite[J].International Journal of Solids and Structures,2015,55:58-65.
[46] Hashemi S,Kinloch A,Willams J.Corrections needed in double-cantilever beam tests for assessing the interlaminar failure of fibre-composites[J].Journal of Materials Science Letters,1989,8(2):125-129.
[47] Hashmi S,Kinloch A J,Williams J G.The analysis of interlaminar fracture in uniaxial fibre-polymer composites[J].Proceedings of the Royal Society of London A Mathematical and Physical Sciences,1990,427(1872):173-199.
[48] Hashemi S,Kinloch A,Williams J.The effects of geometry,rate and temperature on the mode I,mode II and mixed-mode I/II interlaminar fracture of carbon-fibre/poly(ether-ether ketone)composites[J].Journal of Composite Materials,1990,24(9):918-956.
[49] de Morais A B.Mode I cohesive zone model for delamination in composite beams[J].Engineering Fracture Mechanics,2013,109:236-245.
[50] Kusaka T,Hojo M,Mai Y W,et al.Rate dependence of mode I fracture behaviour in carbon-fibre/epoxy composite laminates[J].Composites Science and Technology,1998,58(3-4):591-602.
[51] Kurokawa T,Kusaka T,Shimazaki T,et al.Dynamic interlaminar fracture toughness of CFRP composite laminates[M]//Kawata K.Constitutive relation in high/very high strain rates.1996:217-224.
[52] Blackman B,Hadavinia H,Kinloch A,et al.The calculation of adhesive fracture energies in mode I:revisiting the tapered double cantilever beam(TDCB)test[J].Engineering Fracture Mechanics,2003,70(2):233-248.
[53] Jose S,Ramesh K R,Jana M K,et al.Intralaminar fracture toughness of a cross-ply laminate and its constituent sub-laminates[J].Composites Science and Technology,2001,61(8):1115-1122.
[54] Srawley J E.Wide rage stress intensity factor expressions for ASTM E 399 standard fracture toughness specimens[J].International Journal of Fracture,1976,12(3):475-476.
[55] Sun C T,Han C.A method for testing interlaminar dynamic fracture toughness of polymeric composites[J].Composites Part B:Engineering,2004,35(6-8):647-655.
[56] Davies P,Sims G,Blackman B,et al.Comparison of test configurations for determination of mode II interlaminar fracture toughness results from international collaborative test programme[J].Plastics,Rubber and Composites,1999,28(9):432-437.
[57] Kageyama K,Kimpara I,Suzuli T,et al.Effects of test conditions on mode II interlaminar fracture toughness of four-point ENF specimens[J].Energy,1999,2(2):1-10.
[58] Davidson B D,Sun X,Vinciquerra A J.Influences of friction,geometric nonlinearities,and fixture compliance on experimentally observed toughnesses from three and fourpoint bend end-notched flexure tests[J].Journal of Composite Materials,2007,41(10):1177-1196.
[59] Crews J J H,Reeder J R.A mixed-mode bending apparatus for delamination testing,NASA-TM-100662[R].Hampton:NASA Langley Research Center,1988.
[60] Bhashyam S,Davidson B D.Evaluation of data reduction methods[J].AIAA Journal,1997,35(3):546-552.
[61] Blackman B,Kinloch A,Ro driguez-Sanchez F S,et al.The fracture behaviour of adhesively-bonded composite joints:Effects of rate of test and mode of loading[J].In-ternational Journal of Solids and Structures,2012,49(13):1434-1452.
[62] Szekrényes A,József U J.Comparison of some improved solutions for mixed-mode composite delamination coupons[J].Composite Structures,2006,72(3):321-329.
[63] Rhee K Y,Chi C H.Determination of fracture toughness,GCof graphite/epoxy composites from a cracked lap shear(CLS)specimen[J].Journal of Composite Materials,2001,35(1):77-93.
[64] Ramkumar R L,Whitcomb J D.Characterization of mode I and mixed-mode delamination growth in T300/5208 graphite/epoxy[M]//John W S.Delamination and debonding of materials(A86-20626 07-24).Philadephia:ASTM Press,1985:315-335.
[65] Mathieu F,Aimedieu P,Guimard J M,et al.Identification of interlaminar fracture properties of a composite laminate using local full-field kinematic measurements and finite element simulations[J].Composites Part A:Applied Science and Manufacturing,2013,49:203-213.
[66] Da Silva L F M,Esteves V H C,Chaves F J P.Fracture toughness of a structural adhesive under mixed mode loadings[J].Materialwissenschaft and Werkstofftechnik,2011,42(5):460-470.
[67] Nikbakht M,Choupani N.Fracture toughness characterization of carbon-epoxy composite using Arcan specimen[J].International Journal of Aerospace and Mechanical Engineering,2008,2(4):247-253.
[68] Wang J S,Suo Z.Experimental determination of interfacial toughness curves using Brazil-nut-sandwiches[J].Acta Metallurgica et Materialia,1990,38(7):1279-1290.
[69] Suo Z.Delamination specimens for orthotropic materials[J].Journal of Applied Mechanics,1990,57(3):627-634.
[70] Rikards R,Buchholz F G,Wang H,et al.Investigation of mixed mode I/IIinterlaminar fracture toughness of laminated composites by using a CTS type specimen[J].Engineering Fracture Mechanics,1998,61(3-4):325-342.
[71] Manshadi B D,Farmand-Ashtiani E,Botsis J,et al.An iterative analytical/experimental study of bridging in delamination of the double cantilever beam specimen[J].Composites Part A:Applied Science and Manufacturing,2014,61:43-50.
[72] Kusaka T,Kurokawa T,Hojo M,et al.Evaluation of mode IIinterlaminar fracture toughness of composite laminates under impact loading[J].Key Engineering Materials,1997,141-143:477-500.
[73] Kusaka T.Experimental characterization of interlaminar fracture behavior in polymer matrix composites under lowvelocity impact loading[J].JSME International Journal Series A Solid Mechanics and Material Engineering,2003,46(3):328-334.
[74] Blackman B,Dear J,Kinloch A,et al.The failure of fibre composites and adhesively bonded fibre composites under high rates of test[J].Journal of Materials Science,1995,30(23):5885-5900.
[75] Smiley A,Pipes R.Rate effects on mode I interlaminar fracture toughness in composite materials[J].Journal of Composite Materials,1987,21(7):670-687.
[76] Guo C,Sun C.Dynamic mode-I crack propagation in a carbon/epoxy composite[J].Composites Science and Technology,1998,58(9):1405-1410.
[77] Ravi-shandar K,Knauss W G.An experimental investigation into dynamic fracture:III.On steady-state crack propagation and crack branching[J].International Journal of Fracture,1984,26(2):141-154.
[78] Hug G,Thévenet P,Fitoussi J,et al.Effect of the loading rate on mode Iinterlaminar fracture toughness of laminated composites[J].Engineering Fracture Mechanics,2006,73(16):2456-2462.
[79] Daniel I,Yaniv G,Auser J.Rate effects on delamination fracture toughness of graphite/epoxy composites[M]//Marshall I H.Composite Structures 4 Volume 2 Damage Assessment and Material Evaluation.Berlin:Springer Netherlands,1987:258-272.
[80] Aliyu A,Daniel I.Effects of strain rate on delamination fracture toughness of graphite/epoxy[M]//John W S.Delamination and Debonding of Materials(A86-20626 07-24).Philadephia:ASTM Press,1985:336-348.
[81] Joannic R,Chartier B.A device for utilising the DCB test geometry at intermediate opening velocities[J].Le Journal de Physique IV France,2000,10(9):249-254.
[82] Pardo S,Baptiste D,Fitoussi J,et al.Strain rate effects on the mode I interlaminar fracture of e glass/polyester composites[J].Strain,501:1561-1566.
[83] Blackman B R K,Kinloch A J,Rodriguez-Sanchez F S,et al.The fracture behaviour of structural adhesives under high rates of testing[J].Engineering Fracture Mechanics,2009,76(18):2868-2889.
[84] Colin de Verdiere M,Skordos A A,May M,et al.Influence of loading rate on the delamination response of untufted and tufted carbon epoxy non crimp fabric composites:mode I[J].Engineering Fracture Mechanics,2012,96:11-25.
[85] Thouless M D,Adams J L,Kafkalidis M S,et al.Determining the toughness of plastically deforming joints[J].Journal of Materials Science,1998,33(1):189-197.
[86] Sun C,Thouless M D,Waas A M,et al.Ductile-brittle transitions in the fracture of plastically-deforming,adhesively-bonded structures.Part I:experimental studies[J].International Journal of Solids and Structures,2008,45(10):3059-3073.
[87] Brown S W.Time and temperature-dependence of fracture energies attributed to copper/epoxy bonds[D].Virginia:Virginia Polytechnic Institute and State University,2004.
[88] Xu S Y,Dillard D A.Determining the impact resistance of electrically conductive adhesives using a falling wedge test[J].IEEE Transactions on Component and Packaging Technologies,2003,26(3):554-562.
[89] Simo J C.Response and failure of adhesively bonded automotive composite structures under impact loads[D].Virginia:Virginia Polytechnic Institute and State University,2004.
[90] Karac A,Blackman B R K,Cooper V,et al.Modelling the fracture behaviour of adhesively-bonded joints as a function of test rate[J].Engineering Fracture Mechanics,2011,78(6):973-989.
[91] Syn C J.Dynamic delamination in a glass fiber composite and interfacial fracture in a bi-material[D].West Lafayette:Purdue University,2008.
[92] Wu X F,Dzenis Y A.Determination of dynamic delamination toughness of a graphite-fiber/epoxy composite using Hopkinson pressure bar[J].Polymer Composites,2005,26(2):165-180.
[93] Olsson R,Thesken J C,Brandt F,et al.Investigations of delamination criticality and the transferability of growth criteria[J].Composite Structures,1996,36(3-4):221-247.
[94] Sohn M S,Hu X Z.Comparative study of dynamic and static delamination behaviour of carbon fibre/epoxy composite laminates[J].Composites,1995,26(12):849-858.
[95] Sohn M S,Hu X Z.Impact and high strain rate delamination characteristics of carbon fibre epoxy composites[J].Theoretical and Applied Fracture Mechanics,1996,25(1):17-29.
[96] Liu C,Rosakis A J,Stout M G.Dynamic fracture toughness of a unidirectional graphite/epoxy composite[C]//Proceedings of the Symposium on“Dynamic Effects in Composite Structures”.New York:ASME Press,2001:1-12.
[97] Blackman B,Kinloch A,Wang Y,et al.The failure of fibre composites and adhesively bonded fibre composites under high rates of test[J].Journal of Materials Science,1996,31(17):4451-4466.
[98] Todo M,Nakamura T,Takashi K.Mode II interlaminar fracture behavior of fiber reinforced polyamide composites under static and dynamic loading conditions[J].Journal of Reinforced Plastics and Composites,1999,18(15):1415-1427.
[99] Todo M,Nakamura T,Mada T,et al.Measurement of dynamic interlaminar fracture toughness of FRP laminates using dynamic displacement measuring apparatus[J].Advanced Composite Materials,1998,7(3):285-297.
[100]Todo M,Nakamura T,Takahashi K.Effects of moisture absorption on the dynamic interlaminar fracture toughness of carbon/epoxy composites[J].Journal of Composite Materials,2000,34(8):630-648.
[101]Colin D V M,Skordos A A,Walton A C,et al.Influence of loading rate on the delamination response of untufted and tufted carbon epoxy non-crimp fabric composites/mode II[J].Engineering Fracture Mechanics,2012,96:1-10.
[102]Guo W G,Li Y L,Suo T.Stress wave:an introduction[M].Xi’an:Northwestern Polytechnical University Press,2007:126-146(in Chinese).郭伟国,李玉龙,索涛.应力波简明基础教程[M].西安:西北工业大学出版社,2007:126-146.
[103]Lu W Y,Song B,Jin H.A revisit to high-rate mode-II fracture characterization of composites with Kolsky bar techniques[C]//Proceedings of the 2010 Annual Conference on Experimental and Applied Mechanics.New York:Springer New York,2011:277-279.
[104]Lu W Y,Song B,Jin H.Dynamic mode-II characterization of a woven glass composite[M]//Proulx T.Dynamic behavior of materials.New York:Springer New York,2011:455-457.
[105]Song B,Jin H,Lu W Y.Stress wave propagation in a composite beam subjected to transverse impact[C]//Proceedings of IMPLAST.Bethel:Society for Experimental Mechanics,Inc.,2010:1-3.
[106]Adachi T,Arai M,Sakabe N,et al.Evaluation of dynamic fracture toughness of unidirectional CFRP laminates[J].JSME International Journal Series A Solid Mechanics and Material,2000,43(2):179-185.
[107]Kusaka T,Yamauchi Y,Kurokawa T.Effects of strain rate on mode II interlaminar fracture toughness in carbonfibre/epoxy laminated composites[J].Journal of Physics IV France,1994,4(8):671-676.
[108]Lu W Y,Song B,Gwinn K.Dynamic fracture toughness test using Hopkinson bar[M]//Chalivendra V.Dynamic behavior of materials.New York:Springer New York,2013:499-502.
[109]Wiegand J,Hornig A,Gerlach R,et al.An experimental method for dynamic delamination analysis of composite materials by impact bending[J].Mechanics of Advanced Materials and Structures,2015,22(5):413-421.
[110]Lambros J,Rosakis A J.Dynamic crack initiation and growth in thick unidirectional graphite/epoxy plates[J].Composites Science and Technology,1997,57(1):55-65.
[111]Caimmi F,Frassine R,Pavan A.A new jig for mode II interlaminar fracture testing of composite materials under quasi-static and moderately high rates of loading[J].Engineering Fracture Mechanics,2006,73(16):2277-2291.
[112]Guimard J M,Allix O,Pechnik N,et al.Characterization and modeling of rate effects in the dynamic propagation of mode-II delamination in composite laminates[J].International Journal of Fracture,2009,160(1):55-71.
[113]Govender R,Langdon G S,Nurick G N,et al.Impact delamination testing of fibre reinforced polymers using Hopkinson pressure bars[J].Engineering Fracture Mechanics,2013,101:80-90.
[114]Tsai J L,Guo C,Sun C T.Dynamic delamination fracture toughness in unidirectional polymeric composites[J].Composites Science and Technology,2001,61(1):87-94.
[115]Becker T,Mostafavi M,Tait R,et al.An approach to calculate the J-integral by digital image correlation displacement field measurement[J].Fatigue&Fracture of Engineering Materials&Structures,2012,35(10):971-984.
[116]Upadhyaya P,Singh S,Roy S.A mechanism-based multiscale model for predicting thermo-oxidative degradation in high temperature polymer matrix composites[J].Composites Science and Technology,2011,71(10):1309-1315.
[117]Anthony J,Paris P C.Instantaneous evaluation of J and C[J].International Journal of Fracture,1988,38(1):19-21.
[118]Gunderson J D,Brueck J F,Paris A J.Alternative test method for interlaminar fracture toughness of composites[J].International Journal of Fracture,2007,143(3):273-276.
[119]Xavier J,Oliveira M,Monteiro P,et al.Direct evaluation of cohesive law in mode I of Pinus pinaster by digital image correlation[J].Experimental Mechanics,2014,54(5):829-840.
[120]Dias G F,de Moura M F S F,Chousal J A G,et al.Cohesive laws of composite bonded joints under mode I loading[J].Composite Structures,2013,106:646-652.
[121]Pereira F A M,Morais J J L,Dourado N,et al.Fracture characterization of bone under mode II loading using the end loaded split test[J].Journal of the Mechanical Behavior of Biomedical Materials,2011,4(8):1764-1773.
[122]Dubois F,Méité M,Pop O,et al.Characterization of timber fracture using the digital image correlation technique and finite element method[J].Engineering Fracture Mechanics,2012,96:107-121.
[123]MéitéM,Dubois F,Pop O,et al.Mixed mode fracture properties characterization for wood by Digital Images Correlation and Finite Element Method coupling[J].Engineering Fracture Mechanics,2013,105:86-100.
[124]Lee D,Tippur H,Kirugulige M,et al.Experimental study of dynamic crack growth in unidirectional graphite/epoxy composites using digital image correlation method and high-speed photography[J].Journal of Composite Materials,2009,43(19):2081-2108.
[125]Lee D,Tippur H,Bogert P.Quasi-static and dynamic fracture of graphite/epoxy composites:an optical study of loading-rate effects[J].Composites Part B:Engineering,2010,41(6):462-474.
[126]Blaysat B,Hoefnagels J P M,Lubineau G,et al.Interface debonding characterization by image correlation integrated with Double Cantilever Beam kinematics[J].International Journal of Solids and Structures,2015,55:79-91.
[127]Xu W,Yao X F,Liu D L.The application of coherent gradient sensing interference measurement in static fracture mechanics experiments[J].Optical Technique,2006,32(2):225-233(in Chinese).许蔚,姚学锋,刘栋梁.相干梯度敏感干涉测量技术及在静态断裂力学实验中的应用[J].光学技术,2006,32(2):225-233.
[128]Liu C,Rosakis A,Ellis R W,et al.A study of the fracture behavior of unindirectional fiber-reinforced composite using Coherent Gradient Sensing(CGS)interferometry[J].International Journal of Fracture,1998,90(4):355-382.
[129]Gillespie J W,Jr,Carlsson L A,Pipes R B,et al.Delamination growth in composite materials,NASA-CR-178066[R].Washington,D.C.:NASA,1986.
[130]Gillespie J W,Jr,Carlsson L A,Smiley A J.Rate-dependent mode I interlaminar crack growth mechanisms in graphite/epoxy and graphite/peek[J].Composites Science and Technology,1987,28(1):1-15.
[131]You H,Yum Y J.Loading rate effect on mode Iinterlaminar fracture of carbon/epoxy composite[J].Journal of Reinforced Plastics and Composites,1997,16(6):537-549.
[132]Mall S,Law G E,Katouzian M.Loading rate effect on interlaminar fracture toughness of a thermoplastic composite[J].Journal of Composite Materials,1987,21(6):569-579.
[133]Fracasso R,Rink M,Pavan A,et al.Rate and temperature effects on interlaminar fracture toughness in interleaved PEEK/CF composites[C]//Proceedings of the ECCM-8:European Conference on Composite Materials:Science,Technologies and Applications.Cambridge:Woodhead Publishing Ltd.,1998:463-470.
[134]Sun C,Thouless M D,Waas A M,et al.Ductile-brittle transitions in the fracture of plastically deforming,adhesively bonded structures.Part II:numerical studies[J].International Journal of Solids and Structures,2008,45(17):4725-4738.
[135]Sun C,Thouless M D,Waas A M,et al.Rate effects in mode-II fracture of plastically deforming,adhesively bonded structures[J].Internal Jounal of Fracture,2009,156(2):111-128.
[136]Carlberger T,Biel A,Stigh U.Influence of temperature and strain rate on cohesive properties of a structural epoxy adhesive[J].International Journal of Fracture,2009,155(2):155-166.
[137]May M,Hesebeck O,Marzi S,et al.Rate dependent behavior of crash-optimized adhesives-experimental characterization,model development,and simulation[J].Engineering Fracture Mechanics,2015,133:112-137.
[138]Smiley A J,Pipes R B.Rate sensitivity of mode II interlaminar fracture toughness in graphite/epoxy and graphite/PEEK composite materials[J].Composites Science and Technology,1987,29(1):1-15.
[139]Kageyama K,Kimpara I.Delamination failures in polymer composites[J].Materials Science and Engineering:A,1991,143(1-2):167-174.
[140]Kusaka T,Hojo M,Ochiai S,et al.Rate-dependent mode II interlaminar fracture behavior of carbon-fiber/epoxy composite laminates[J].Materials Science Research International,1999,5(2):98-103.
[141]Berger L,Cantwell W J.Temperature and loading rate effects in the mode IIinterlaminar fracture behavior of carbon fiber reinforced PEEK[J].Polymer Composites,2001,22(2):271-281.
[142]Cantwell W.The influence of loading rate on the mode II interlaminar fracture toughness of composite materials[J].Journal of Composite Materials,1997,31(14):1364-1380.
[143]Maikuma H,Gillespie J W,Jr,Whitney J M.Analysis and experimental characterization of the center notch flexural test specimen for mode II interlaminar fracture[J].Journal of Composite Materials,1989,23(8):756-786.
[144]Blackman B R K,Dear J P,Kinloch A J,et al.The failure of fibre composites and adhesively bonded fibre composites under high rates of test[J].Journal of Materials Science,1996,31(17):4467-4477.
[145]Compston P,Jar P Y B,Burchill P J,et al.The effect of matrix toughness and loading rate on the mode-IIinterlaminar fracture toughness of glass-fibre/vinyl-ester composites[J].Composites Science and Technology,2001,61(2):321-333.
[146]Jiang W,Tsang F F Y,Tjons S C,et al.Loading rate dependence of mode II fracture behavior in interleaved carbon fibre/epoxy composite laminates[J].Applied Composite Materials,2001,8(6):361-369.
[147]Wade G A,Cantwell W J.Temperature and loading rate effects on the fracture behaviour of adhesively bonded GFRP Nylon-6,6[J].The Journal of Adhesion,2001,76(3):245-264.
[148]Banea M D,de Sousa F,Da Silva L,et al.Effects of temperature and loading rate on the mechanical properties of a high temperature epoxy adhesive[J].Journal of Adhesion Science and Technology,2011,25(18):2461-2474.
