深厚覆盖层上水闸结构-地基体系动力反应特性研究

邸庆霜，胡 晓，邢义川，曾 迪

（1.中国水利水电科学研究院 工程抗震研究中心，北京 100048；2.中国水利水电科学研究院 研究生部，北京 100048）

深厚覆盖层上水闸结构-地基体系动力反应特性研究

邸庆霜1，胡 晓1，邢义川2，曾 迪1

（1.中国水利水电科学研究院 工程抗震研究中心，北京 100048；2.中国水利水电科学研究院 研究生部，北京 100048）

高抗震设防烈度区的水闸工程，需要采用动力设计方法进行结构设计。对于建于深厚覆盖层地基之上的大多数水闸结构，本文采用等效线性化方法，在总体动力学效应大致相当的意义上，将水闸结构-地基体系中土体非线性问题转换为线性问题进行求解。以某水闸工程为例开展对比分析研究，发现：（1）相对于弹性地基模型，考虑地基土非线性的等效线性化方法可以获得更为合理的水闸结构动力反应；（2）上部机架桥部分的动力反应要比闸墩部分高，在水闸设计过程中应当强化上部机架桥部分的结构设计；（3）对于考虑深厚覆盖层的水闸抗震问题，应当更加深入研究长周期地震动输入的影响；（4）等效线性化方法是考虑了地基土非线性动力特性，工程基础数据及经验较为丰富，也便于扩展为考虑滞回特性的完全动力非线性求解方法。

水闸；土-结构动力相互作用；深厚覆盖层；土体动力本构；等效线性化方法

1 研究背景

水闸工程量大面广，如果遭受地震破坏，将会丧失正常运行功能，甚至危及社会公共安全。国内汶川、唐山、海城、喀什、邢台等典型地区的震害调查显示，地震对水闸的破坏较其他水工建筑物相对更严重。根据现行《水工建筑物抗震设计规范SL203-97》和《水工建筑物抗震设计规范DL5073-2000》中规定：设计烈度为8、9度的1、2级水闸或地基为可液化土的1、2级水闸应采用动力法进行抗震计算。

目前大部分水闸工程建于深厚覆盖层的软土或砂砾石地基之上，甚至部分水闸工程下部地基为可液化土层。在地震动循环荷载作用下，岩土材料会表现出复杂的非线性动应力-应变关系［1］。此外，上部结构的振动能量会通过无限地基介质向外传递，使结构的振动减小，称之为无限地基的辐射阻尼效应［2-3］。保障水闸工程抗震能力，主要是保障地基的稳定，不发生液化或底板的不均匀沉降［4］。

由此可见，建立合理的地基土模型对水闸结构-地基体系的动力响应机制研究至关重要，这就需要探索一套适用于水闸结构动力分析设计分析方法。目前大部分水闸结构的抗震动力分析中，传统的无质量地基模型能够考虑地基刚度对结构动力响应的贡献，但是无法考虑结构-地基体系的惯性动力作用以及地基辐射阻尼等非线性动力效应。

1968年，Seed首先提出用等效线性化方法［5-6］近似考虑土体的非线性和耗能特性。该方法以共振柱仪和动三轴仪实验所获得的动剪切模量-剪应变关系［7］和阻尼比-剪应变关系形式给出地基土体的粘弹性动力本构模型，大致分为Hardin-Drnevich模型［8］与Ramberg-Osgood模型两大类。在总体动力学效应大致相当的意义上，用一个等效的剪切模量G和等效阻尼比λ替换所有不同应变幅度下的剪切模量和阻尼比，将土体非线性问题转换为线性问题，由波动分析的频域（或时域）迭代完成求解过程。

等效线性化方法以实验成果作为基础、形式直观简便、无需建立复杂的应力-应变滞回动力关系，此外，大量工程经验数据的积累使等效线性化方法［1］在场地地震反应分析、地下结构物地震稳定性分析、土-结构体系动力相互作用分析中有着广泛的应用。

本文以某水闸工程为例，考虑深厚覆盖层地基土体非线性动力特性的影响，采用等效线性化方法进行水闸结构-地基体系的地震动力响应求解，通过对比分析常规弹性地基模型与等效线性化方法模型的结果规律，探讨了水闸结构-地基体系地震响应的特性以及等效线性化求解方法的应用，为水闸结构-地基体系动力分析及抗震性能的研究提供参考。

2 时域等效线性化方法

2.1 系统方程对于水闸结构-地基体系进行地震动力时域反应分析时，采用有限元方法进行离散处理后的动力平衡方程，如下式：

对于考虑地基土动力问题，可以采用时域的滞后阻尼模型［9］，即：

式中：fc为滞后阻尼的转换频率。

2.2 土的动力本构模型地基土的动力性能可以采用由共振柱仪和动三轴仪实验获得的动剪切模量比-剪应变关系（G/Gmax-γ）和阻尼比-剪应变关系（λ-γ）来描述［7］。Hardin等［8］预测动剪切模量G与动剪应变γ符合双曲线关系，从而提出著名的Hardin-Drnevich模型，即：

式中：γref为参考剪应变，通常取动剪切模量比为0.5时所对应的剪应变幅值。

这种土动力试验成果本质上刻画了地震动力荷载作用下土体动应力-应变关系全过程的基本特征：“骨架曲线”和“滞回曲线”［10］。

2.3 等效线性化求解［1，5-6］在采用时域的等效线性化方法进行结构-地基土系统动力求解时，其基本求解流程可以表述如下：（1）初次静力计算，确定模型中地基土各单元震前剪应变幅值，并计算动剪切模量的初值。阻尼比初值取一个较小值0.05或0；（2）根据确定的各单元动剪切模量 G和阻尼比λ值修正模型材料参数定义；（3）进行水闸结构-地基体系的地震动力时程反应求解；（4）提取模型中地基土各单元的动剪应力τd和动剪应变 γd时程曲线数据；（5）从动剪应变γd时程曲线中确定最大动剪应变幅值（γd）max，根据经验，通常取有效剪应变为最大动剪应变的0.65倍，即（γd）eff=0.65（γd）max；（6）根据（5）中确定的各单元有效剪应变幅值，进行迭代误差判断，即前后两次等效线性化迭代过程的有效剪应变幅值的差是否小于收敛限值？如果小于收敛限值，则该单元不再更新材料动剪切模量和阻尼比参数；否则在对应地基土层的动剪切模量比G/Gmax和阻尼比与剪应变γ关系曲线中进行插值，确定各单元新的动剪切模量G和阻尼比λref；（7）如果所有单元的剪应变幅值迭代误差均满足收敛条件，则等效线性化迭代过程结束。否则返回第（2）步重新进行计算，直到所有单元均满足迭代收敛误差条件，则完成等效线性化迭代求解过程。

等效线性化由于简化了土体的滞回动力特性，仅需几次弹性时程迭代分析便可满足计算收敛终止条件，具有较高的计算效率。对于规模较大的模型，还可采用地基土模型的单元分区聚合方法进一步提高计算效率，即一个子分区内的土体单元集合仅取其中某一主控单元作为更新该分区内单元材料动剪切模量和阻尼比参数的计算依据。

3 工程实例模型

3.1 工程概况某水闸工程为平原地区河道枢纽水闸，由闸室、上游铺盖及翼墙、下游消力池及翼墙、海漫等组成。闸室共15孔，每孔净宽10.0m，闸室长13.5m，中墩厚度1.3m，水闸总宽180.8m。

闸墩高8m，上部机架桥高度8.28m。每道闸室内均设工作和检修闸门各一道，工作门为平面钢质闸门，宽度10m，高度7.5 m，检修闸门为叠梁式钢质平面闸门。该水闸为大型2级水闸工程，抗震设防烈度为9度，设计基本加速度0.4 g，场地类别为Ⅱ类。水闸主体结构钢筋混凝土参数见表1所示，水闸地基土分层参数见表2所示，相应的动剪切模量比与阻尼比曲线见图1。

表1 填水闸结构钢筋混凝土参数

表2 地基土分层物理、几何参数

图1 地基土体动力学参数

根据水闸顺河向的设计资料，建立顺河向的二维水闸结构-地基体系计算模型。为考虑地震波在地基土层中的波动传播特性，地基土层中网格的选取依据以下原则：（1）对于竖向单元尺寸，为避免离散有限元对地震波中有效频率分量的滤波作用，一般要求竖向单元长d≤（1/8～1/12）λmin，λmin为土层中地震波有效频率分量中的最小波长。本文以有效频率10 Hz来确定最小波长；（2）对于水平向的模型地基范围，考虑到土介质的阻尼性质［7］，竖向人工边界设置在距离近场区5倍土层深度远处，这样可以忽略人工边界对近场地震反应的影响。

地基土进行等效线性化分区之后的计算模型如图2所示。

图2 计算模型及场地土等效线性化迭代分区

3.2 模型求解在计算过程中分别选用El Centro波、Taft波、Kobe波等3条地震波，见图3所示。根据动力特性分析确定水闸结构-地基体系的前三阶自振频率分别为1.55、2.25和2.51 Hz，模态见图4所示。

图3 输入地震波及傅氏谱

图4 水闸结构-地基体系模态

在后续分析过程中，分别采用“线弹性”与“等效线性”地基模型两种计算方案，以此来分析讨论水闸结构-地基相互作用体系的动力响应特性以及深厚覆盖层地基土体非线性因素对结构反应的影响，同时考察等效线性化方法的应用问题。计算结果的输出位置包括闸室底板（94）、闸墩顶部（1281）、机架桥顶部（1560）以及靠近水闸结构的场地上（8682）、下（10259）游两侧地表点，如图2所示。输出的计算结果为各输出点的绝对加速度放大系数与绝对位移响应，见表3。表中差异项是以线弹性结果为基准进行计算。

根据三种不同地震波输入时的计算过程，迭代至收敛的次数分别为5、4、5。可见，采用等效线性化方法可以在少数几次线弹性时程动力分析的过程中考虑地基土体的非线性特性完成水闸结构-地基土体系的动力求解，这将有助于提高动力分析的效率。

三种不同地震波输入条件下，机架桥顶部相对闸室底板的相对位移和相对加速度时程结果，分别见图5和图6所示。图7为3种不同地震动输入条件下，上游侧场地地表加速度反应时程结果。

表3 不同水闸部位的动力反应结果

根据表3所列结果可以看到，线弹性方法所得上部结构的加速度动力放大系数要远大于等效线性化方法，最大差异达到81.13%，两种方法所得绝对位移响应的最大差异相对较小，达39.08%。这两点也可以从机架桥顶部相对位移（图5）和相对加速度（图6）时程结果看到。相对于弹性地基模型结果，考虑地基土的非线性动力特性后，可以获得更为合理的水闸结构动力反应。此外，由表3所列等效线性化结果可以看出，上部结构中机架桥的动力放大系数最大，其值为Kobe波结果的2.71，闸室底板和闸墩顶的动力放大系数基本相同，最大值为2.16。在水闸设计过程中应当强化上部机架桥部分的结构设计以及相应抗震构造措施。

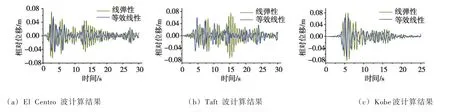
图5 机架桥顶部相对位移时程

图6 机架桥顶部相对加速度时程

图7 场地上游地表点加速度时程

对于地表反应，EL波和Taft波的加速度放大系数结果较大，线弹性与等效线性化方法的结果差异在50%左右，采用两种方法计算所得Kobe波结果差异很小。等效线性化结果中，地表加速度放大系数是Kobe波结果最大，EL波和Taft波结果略小，三种地震波结果差异较小。说明场地的地震反应受地震动输入的影响更为明显。综合表3中各项结果，Kobe波计算结果相比EL波和Taft波结果要大，这主要是由于Kobe波的主频成分相对集中地分布于水闸-结构体系自振频率附近（见图3（f））的低频长周期段。在后续研究中应当更加关注此类深厚覆盖层上结构长周期地震动输入的相关问题研究。

4 结论

本文针对高抗震设防烈度区的水闸工程，考虑深厚覆盖层地基土体非线性动力特性的影响，分析了水闸结构-地基土体的等效线性化动力求解理论，之后以某水闸工程为例，开展对比分析研究，发现：（1）相对于弹性地基模型结果，考虑地基土的非线性动力特性后，可以获得更为合理的水闸结构动力反应；（2）上部机架桥部分的结构反应要比闸墩部分高，在水闸设计过程中应当强化上部机架桥部分的结构设计；（3）对于考虑深厚覆盖层的水闸抗震问题，应当更加深入研究长周期地震动输入的影响；（4）等效线性化方法是考虑了地基土非线性动力特性，工程基础数据及经验较为丰富，也便于扩展为考虑滞回特性的完全动力非线性求解方法。

［ 1］ 廖振鹏，李小军.地表土层地震反应的等效线性化解法［C］//地震小区划（理论与实践）.北京：地震出版社，1989.

［ 2］ 王进廷，潘坚文，张楚汉 .地基辐射阻尼对高拱坝非线性地震反应的影响［J］.水利学报，2009，40（6）：413-420.

［ 3］ 李志全，杜成斌，艾亿谋.地基辐射阻尼对结构地震响应的影响［J］.河海大学学报：自然科学版，2009，37（4）：400-404.

［ 4］ 林皋.汶川大地震中大坝震害与大坝抗震安全性分析［J］.大连理工大学学报，2009，49（5）：657-666.

［ 5］ Seed H B，Idriss IM.The influence of soil conditions on ground motions during earthquake［J］.Journal of the SoilMechanics and Foundation Engineering Division，ASCE，1969，94（1）：93-137.

［ 6］ 齐文浩，薄景山.土层地震反应等效线性化方法综述［J］.世界地震工程，2007，23（4）：221-227.

［ 7］ 陈国兴，谢君斐，张克绪 .土的动模量和阻尼比的经验估计［J］.地震工程与工程振动，1995，15（1）：73-84.

［ 8］ Hardin B O，Drnevich V P.Shearmodulus and damping in soil：design equations and curves［J］.Journal of the SoilMechanics and Foundation Engineering Division，ASCE，1972，98（7）：667-692.

［ 9］ 楼梦麟，潘旦光.滞后阻尼在土层时域分析中的应用［J］.同济大学学报，2004，32（3）：281-285.

［10］ 张如林，楼梦麟.基于达维坚科夫骨架曲线的软土非线性动力本构模型研究［J］.岩土力学，2012，33（9）：2588-2564.

Seismic response analysis of sluice structure-soil system with deep soil deposit

DI Qingshuang1，HU Xiao1，XING Yichuan2，ZENG Di1
（1.Earthquake Engineering Research Center，IWHR，Beijing 100048，China；2.Section of Postgraduate Education，IWHR，Beijing 100048，China）

Dynam ic analysis method is needed for high seismic demand of sluice structures.Usually，sluice structures were commonly built on the soil layer with deep deposit.For the reason of complexity of such problems and engineering practices，the equivalent linear method was adopted in the dynamic response anal⁃ysis of sluice structure-soil deposit system.On the statistic equivalent concept，the nonlinearity of soil mate⁃rial was addressed with linear solution method，so the problem was simplified.Concluding froma sluice structure analysis，that（1） comparing to the normal elastic solution，rational results can be obtained by equivalent linear method which considering nonlinearity of foundation soil，（2）the response of upper frame was bigger than the sluice pier，which need much more concern in the structure design，（3）when consid⁃ering deep deposit soil layers，the effects of seismic inputs with long periods should be more concerned，（4） equivalent linear method take considering nonlinearity of soils by statistical equivalent method，with many engineering test data and experiences，it also convenient to expand to true nonlinear material model method.

sluice structure；soil-structure interaction；deep soil deposit；dynamic soil model；equivalent linear method

TV312

：Adoi：10.13244/j.cnki.jiwhr.2015.05.001

1672-3031（2015）05-0321-06

（责任编辑：李 琳）

2015-03-19

中国水利水电科学研究院青年科技专项（抗集1306）

邸庆霜（1982-），男，河北保定人，博士后，工程师，主要从事结构抗震研究。E-mail：diqs@iwhr.com