防水工程质量保证保险费率厘定研究

杨 帆 洪文霞 魏小朝 杨 昭

青岛理工大学管理学院



防水工程质量保证保险费率厘定研究

杨 帆 洪文霞 魏小朝 杨 昭

青岛理工大学管理学院

建筑行业素有“结构第一，防水第二”的说法。建筑防水质量的优劣直接影响建筑结构的安全性，更关系到业主的日常使用和生命财产安全。但我国防水行业乱象丛生，质量问题亟待解决。而建立防水工程质量保证保险体系是彻底解决我国目前防水质量问题的必由之路。

一、引言

防水工程作为建筑工程的一个重要环节，不仅关系到建筑物的结构安全性能，对建筑的使用功能及环境卫生等也有很大影响。保证建筑物或构筑物在合理的设计使用年限内，能够正常使用，避免遭受水的侵蚀，为使用者提供一个舒适安全的环境，是建筑防水工程最重要的功能(柳明，2014)。近年来，我国城市建设步伐的加快推动了建筑行业的迅速发展，各类工程项目层出不穷，而一些建筑公司为了谋取利润，对质量的管理流于表面，往往只做表面文章，建筑渗透问题频现，不仅影响人们的日常使用，也使用户与业主之间矛盾不断。为了解决防水工程的质量问题，国外探索出了一条建立防水工程质量保证保险制度的道路，防水工程的质量得到了改善。而目前我国针对建筑防水工程质量的问题采取的是5年保修期制度和5%的质量保证金制度。但是5%的质量保证金与建造劣质工程所带来的利润相比，微不足道。5年保修期相对于住宅的70年产权也明显偏短。事故代价过低使一些建筑企业钻了制度的空子，出现渗漏只要修补就行，保修期和质保金变成了防水工程质量问题的许可证。学习国外的先进经验，建立防水工程质量保证保险制度才是解决建筑防水工程质量问题的终极之道(朱东清，2014)。

如果能探寻一个合理厘定防水工程质量保证保险费率的方法，作为工程质量保证保险的附加保险进行推广，将会对建筑企业起到一定的约束作用，同时促进防水材料供应商的优胜劣汰，从根本上改善我国防水工程的质量状况。鉴于此，本文引入统计理论确立了基准费率，并以模糊综合评价法(FCE )对基准费率进行修正。

二、计算防水工程质量保证保险基准费率

(一)基于统计理论的基准费率厘定

统计理论是传统费率厘定的精算定价方法。其基本原理为：

p=E(S)=E(N)·E(X)

(1)

i0=纯保费率=P/n

(2)

其中，P代表纯保费；S为赔付成本的随机变量；i0代表基准费率；N代表理赔频率；X代表一次索赔的赔付额；n代表风险单位个数。

(二)估算赔付额

对损失数据进行统计分析，运用SPPS软件拟合出损失数据的分布函数F(X)及损失密度函数f(x)，建立概率密度曲线。由此得到保险标的的单位期望赔付额E(X)。

(三)估计理赔频率

《2013年全国建筑渗漏状况调查项目报告》显示，国内主要城市建筑屋面渗漏率高达95.33%。有必要将建筑防水工程质量保证保险在建筑行业新建项目强制推行，即该行业所有建筑企业均作为投保人，则风险单位个数可近似假设为该行业建筑企业数。运用crystalball软件进行拟合得到期望理赔频率E(N)。

最终由公式(2)计算基准费率i0。

三、计算防水工程质量保证保险风险调整系数

i0是基准费率，是基于共性的费率，必须重新调整费率结构，即由一个调整系数乘以基准费率得到基于个体的保险实际费率：

i=i0×a

(3)

(一)建立防水工程质量风险评估指标体系

本文从建设单位、材料供应商、项目特性三个方面综合考虑对防水工程质量风险的影响，建立了因素集X=(X1,X2,X3)，因素集下的指标集：Xi=(xii,xi2,…,xij),其中，i=1,2,3,j为因素下指标的个数。构建的防水工程质量风险评估指标层次结构体系如下表所示。

(二)定义评价集

定义评价集是为了确定防水工程质量保证保险费率调整系数，我们将建筑工程渗透风险分为五个等级：V=[V1,V2,V3,V4,V5]=(很低，较低，一般，较高，很高)。风险高于平均水平则调整系数大于1，风险越高系数越大；反之，风险低于平均水平时，调整系数小于1，风险越低系数越小。则对应的风险评价值C=(0.6，0.8，1.0，1.2，1.4)。

(三)防水工程质量风险模糊综合评价

模糊层次分析法以模糊数学隶属度理论为基础，将定性评价转化成定量的方式处理，能很好地解决难以量化的问题，但在指标权重分配上主观性较强。而熵权法利用各指标的变异程度，通过计算各指标的信息熵来进行权重分配，充分反映了指标数据自身所携带的信息，更具客观性。因此，本文提出熵权与模糊层次分析法耦合的风险评估模型，计算过程如下：

表 防水工程质量保证保险风险评估指标体系

防水工程利益相关方众多，不同领域的专家对防水工程质量风险会有不同的认识，综合各方意见有利于确保风险评估的客观公正性。故选取分别来自政府、防水协会、工程建设专家等20人组建专家组对某建筑防水工程的质量风险进行评价。得到该项目防水工程风险的初始化指标集隶属矩阵：

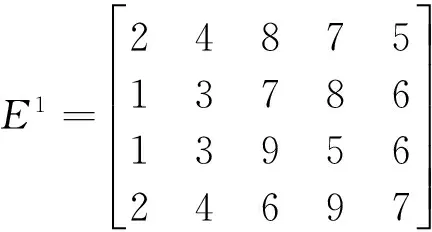
因子集X中各因子在防水工程质量风险综合评价中的重要性程度不同，不同权重会对评价结果有不同程度的影响，须对参与评价的指标因子进行赋权。

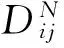
(4)

(5)

4.由熵权法计算各指标的权重，公式如下：

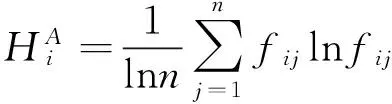
(6)

(7)

5.由公式(8)计算加权规范化指标集隶属矩阵：

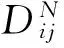
(8)

因素X1下的指标加权规范化隶属矩阵计算过程如下：

由公式(4)计算E1归一化隶属矩阵D1：

由公式(5)计算E1规范化隶属矩阵R1:

由公式(8)计算指标评价向量：

同理可得：

6.确定因素集隶属矩阵B:

7.由公式(5)、(6)、(7)计算因素集的权重向量：

8.计算风险指数即调整系数：

a=V×CT=1.114

(四)评价结果

保险产品作为特殊的商品，合理厘定具有差别化的防水工程质量保证保险费率是形成该保险市场的前提。通过对该项目的防水工程质量风险的评估得出其风险高于平均水平，则其保险费率i=i0(基准费率)×1.114。

四、结论

防水工程质量保证保险作为我国一个新兴的保险类型，在制度和政策上都有很多的不足，本文针对防水工程质量保证保险费率的合理厘定，以统计理论为基础，采用修正系数的形式建立了防水工程质量保证保险费率的厘定模型。本文主要结论有：

第一，引入统计理论，针对新型险种费率的厘定具有科学性和适应性，同时满足保险费率厘定原则的大数法则。

第二，通过运用模糊综合评价法，从保险公司的角度进行费率的修正。这样做同样也具有科学性，同时体现了防灾防损的特性，为构建健康稳定的建筑行业环境提供了保障。

第三，通过研究分析，得出建筑防水工程质量保证保险费率的厘定程序和基本计算模型，有利于我国建筑防水工程质量保证保险的推广。

第四，对于基准费率的厘定，文章仅是给出了计算模型，而未进行实际验算，且基准费率为纯保费率，未考虑利润、管理等其他因素。故精确的基准费率厘定有待进一步研究。