全国近岸海域水质空间插值算法精度分析

2015-04-26李俊龙刘喜惠刘海江李铭煊高锋亮

中国环境监测 2015年2期

李俊龙，丁页，刘喜惠，刘方，李曌，陈平，刘海江，李铭煊，高锋亮

中国环境监测总站，国家环境保护环境监测质量控制重点实验室，北京 100012

近岸海域环境要素的空间分布和表征技术研究是开展环境监测和评价，构建中国近岸海域环境监测技术体系的重要组成部分［1］。空间插值技术形成于20世纪50年代，理论体系不断完善［2-4］，尤其在大尺度环境要素的分析和表征方面，空间插值技术具有明显的优势和价值［5-7］。近岸海域环境要素具有空间相关性、依赖性和异质性，因此，在现阶段人力、财力和技术装备能力有限的情况下，空间插值技术对于评估采样点周围空白区域的环境属性信息十分重要［8-10］。随着地理统计科学的迅速发展，空间插值算法已有很多，但各种算法与近岸海域环境监测站位的匹配性、准确性和适用性分析成为难题，相关研究也较少见，制约了空间插值技术在环境监测领域的应用。为提高空间插值算法应用的科学性，更准确地评价和表征近岸海域环境质量，基于实测历史数据，通过对3种插值算法13种模型模拟值与实测值的比较和分析，优化和筛选出实际偏离程度最小的插值模型，从而为空间插值技术在近岸海域环境监测领域中的应用提供参考和借鉴。

1 实验部分

1.1 数据来源

研究区域为全国近岸海域，根据国家环境保护部《全国近岸海域环境质量监测实施方案》，按照网格布点法，确定299个国控站位，面积约28万平方公里。

海水水质数据来源于全国近岸海域环境监测网2009年监测数据，监测项目包括水温、悬浮物、盐度、pH、溶解氧、化学需氧量、石油类、活性磷酸盐、无机氮、汞、铜、铅、镉、非离子氨和六价铬等。

基础地理信息数据根据国家测绘局1∶25万标准分幅地图加工而成。

1.2 水质评价方法

各站位的污染物浓度采用年度平均值，根据《海水水质标准》(GB 3097—1997)［11］和《近岸海域环境监测规范》(HJ 442—2008)［12］，按照单因子判别法进行水质评价，即某一测点海水中任何评价指标超过一类海水标准的，该测点水质即为二类，超过二类海水标准的即为三类，依次类推［13］。

1.3 空间插值方法

1.3.1 反距离加权(IDW)

IDW法是一种基于相近相似原理的确定性插值方法，假设每个采样点有一个局部影响，与未采样点距离最近的若干个点对未采样点值的贡献最大，其贡献与距离成反比，表达式为

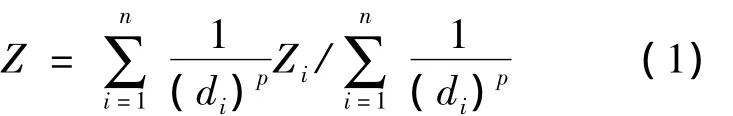
式中:Z是评估的海水水质;Zi是站位i(i=1，2…n)的海水水质;d是评估站位和采样站位之间的距离;p是分析定义的幂参数;n代表用于评估计算用的站位数量。

影响IDW法准确度的主要因子是p值［14］，当p等于1时，是线性距离衰减插值;当p大于1时，是非线性距离衰减插值。对较大的幂，较近的采样站位被给定较高的权重份额;对较小的幂，权重比较均匀地分配给各采样站位。该法的优点是可通过权重调整空间插值等值线的结构，缺点是如不了解研究区域内插属性的结构分布特征，不合理的加权会导致较大的偏差，而且易受极值的影响。研究采用常用的几个p参数(p=1，2，3，4，5，6［2，15］)的模拟计算结果进行比较。另外，临近点的大小和数量同样影响结果的准确性，最近采样点值取12，范围设置 Maximum distance为1.7。

1.3.2 样条函数法(Spline)

Spline法是用数学函数来逼近曲面的一种方法，就是按一定的光滑性要求对接起来的分段多项式。该方法计算量小，速度快，保留了局部的变化特征，有较好的视觉效果，适合于平滑的表面，一般要求有连续的一阶和二阶导数;其缺点是难以对函数内插的误差进行估算，点稀疏时效果不好，对有限的监测数据模拟，Spline法难以满足内插的精度，表达式为

式中:Z为估算值;n为站位数;λ为一系列线性方程解的系数;ri是估算点到i站位的距离;R(ri)和T(x，y)的表达式为

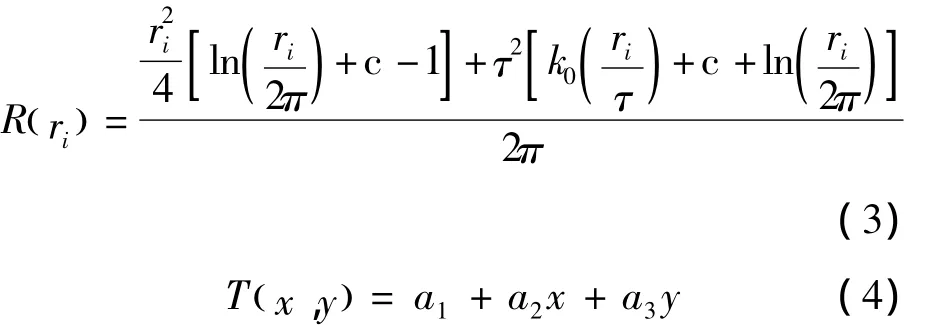
式中:τ为权重系数;k0为改正后的贝塞尔函数;c为常数;a为线性方程的系数。分别采用Regularized和Tension 2种类型的Spline法进行插值验证，权重系数取0.1，模型样点个数取12。

1.3.3 克里格方法(Kriging)

Kriging法是建立在地统计学基础上的一种插值方法，该算法以区域化变量理论为基础，认为任何在空间连续性变化的属性是不规则的，不能用简单的平滑数学函数进行模拟，可用随机表面给予较恰当的描述。Kriging法着重于权重系数的确定，从而对空白站位的变量值提供最好的线性无偏估计，公式为

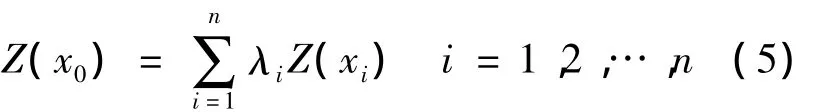
式中:λi是站位i海水水质Z(xi)的权重系数，表示各站位海水水质Z(xi)对估计值Z(x0)的贡献。为达到线性无偏估计，使估计方差最小，权重系数由方程组求得:

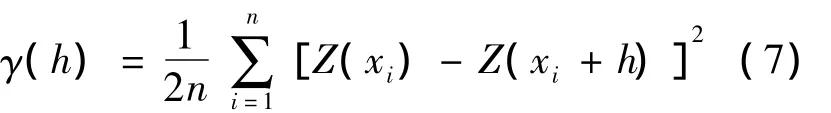
式中:Z(xi)是站位i的海水水质;Z(xi+h)是距离i站位h的点的水质;n代表距离为h的成对站位的数目。根据实验半变异函数，确定合理的变异函数理论模型。分别采用 Spherical、Circular、Exponential、Guassian、Linear 5 个变异函数模型进行验证，最近采样点取值12，范围设置 Maximum distance为1.7。

1.4 插值结果准确度检验

利用交叉检验法［16-17］验证各插值模型的模拟效果。其原理为每个监测站位的海水水质都从数据列中去掉一次，其海水水质由周围站位的实测值通过插值来估算，然后计算站位模拟值与实测值之间的误差。采用模拟值与实测值的pearson相关系数(Corr)、平均误差(ME)、平均绝对误差(MAE)和均方差(RMSE)作为评估插值方法的标准。Corr反映验证值与模拟值之间的吻合程度，ME反映总体模拟值误差的大小，MAE反映模拟值可能的误差范围，RMSE反映模拟值的灵敏度和极值效应，公式为

式中:C(xi，yi)为测站样本点之间的协方差;C(xi，x0)为测站样本点与插值点之间的协方差，μ为拉格朗日乘子。

插值数据的空间结构特性用半变异函数γ(h)表示:

1.5 交叉检验的实现

利用 Visual Studio．NET 2005开发平台，C++语言和ArcGIS Engine组件编写程序，根据坐标文件生成矢量图层，对图层中各站位实现循环，分别去除一个站位，利用剩余站位进行插值计算，生成栅格图层，再从该图层中提取去除点的插值结果，进行误差统计。

1.6 数据统计、插值的实现

数据的统计、相关分析采用SPSS 13.0。插值计算采用ArcGIS Desktop 9.2，Albers双标纬等积圆锥投影，Krasovsky椭球体，D_Krasovsky_1940大地基准面，中央经线105°，标准纬线25°和47°。

最优插值模型与其他模型用RI进行比较:

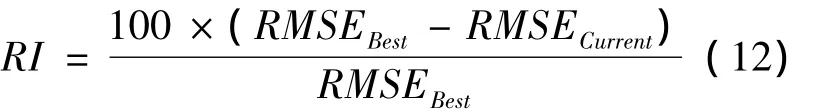
2 结果与讨论

2.1 模拟海水水质分布

将各插值模型的模拟结果进行栅格化处理，形成全国近岸海域水质分布图(图1)。

由图1可见，所有插值模型模拟的海水水质污染程度都由近岸向远海递减。这与中国近岸海域环境问题的实际情况相符，近海水体中污染物浓度主要受陆源径流的影响，总体呈现近岸高、远岸低的趋势特征;主要超标污染物是无机氮和活性磷酸盐，长江口、黄河口、珠江口、海河口和闽江口等及邻近海域受陆源输入影响，富营养化程度较严重［18］。相比较，Spline-Regularized法在广西北部湾海域的模拟结果为污染程度严重，相对该海域水质的实际水平有所高估，说明其在局部海域水质的插值模拟效果较差。

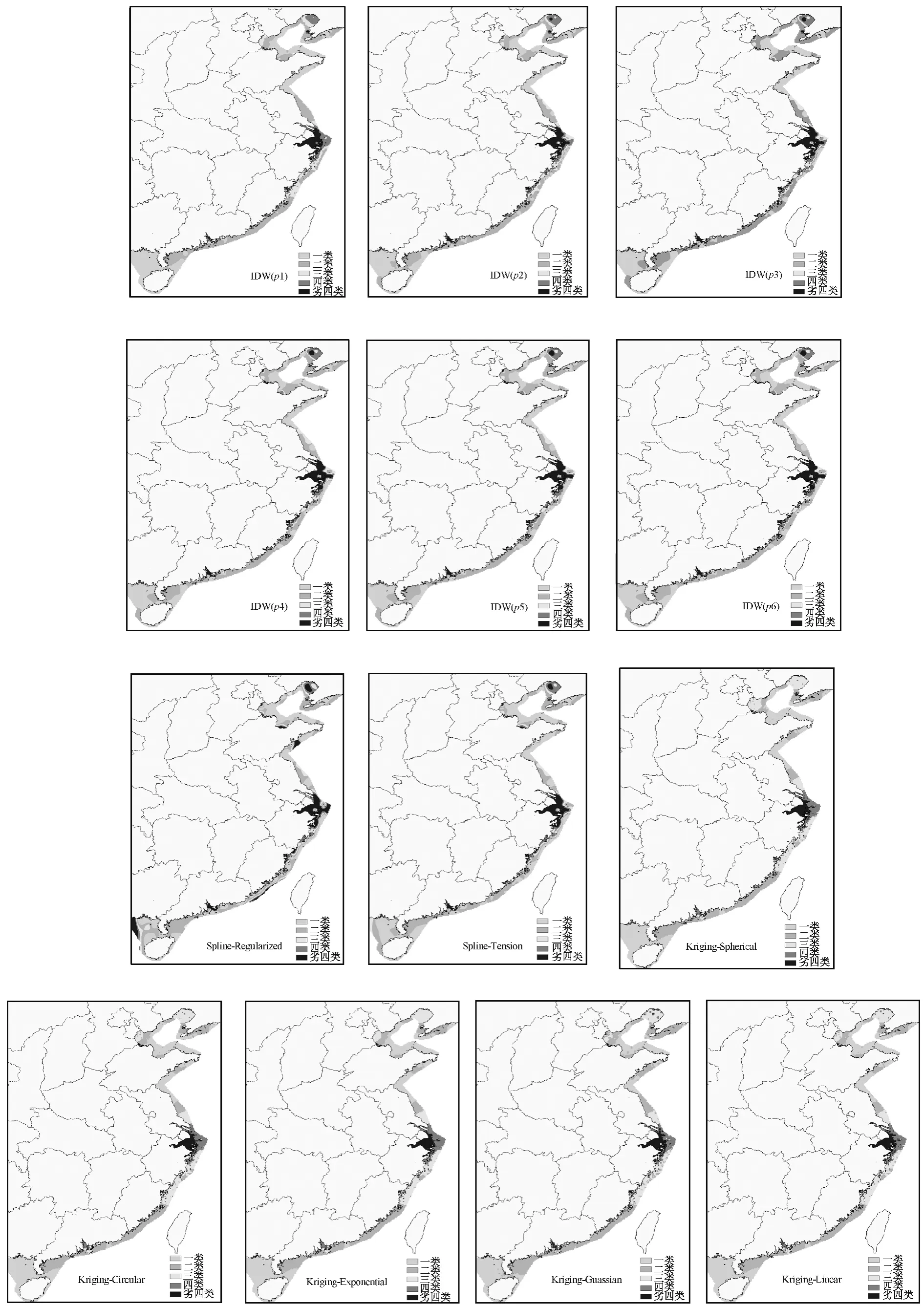
图1 不同插值模型的近岸海域水质模拟结果

2.2 模拟结果误差分析

交叉检验统计各插值模型的误差结果(表1)。

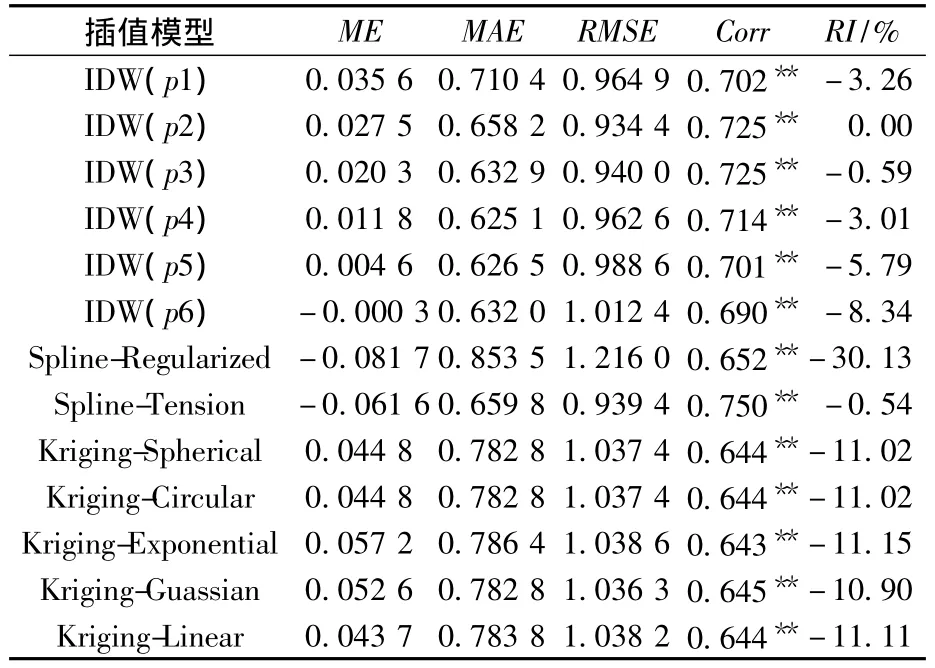
表1 不同插值模型的交叉检验误差结果

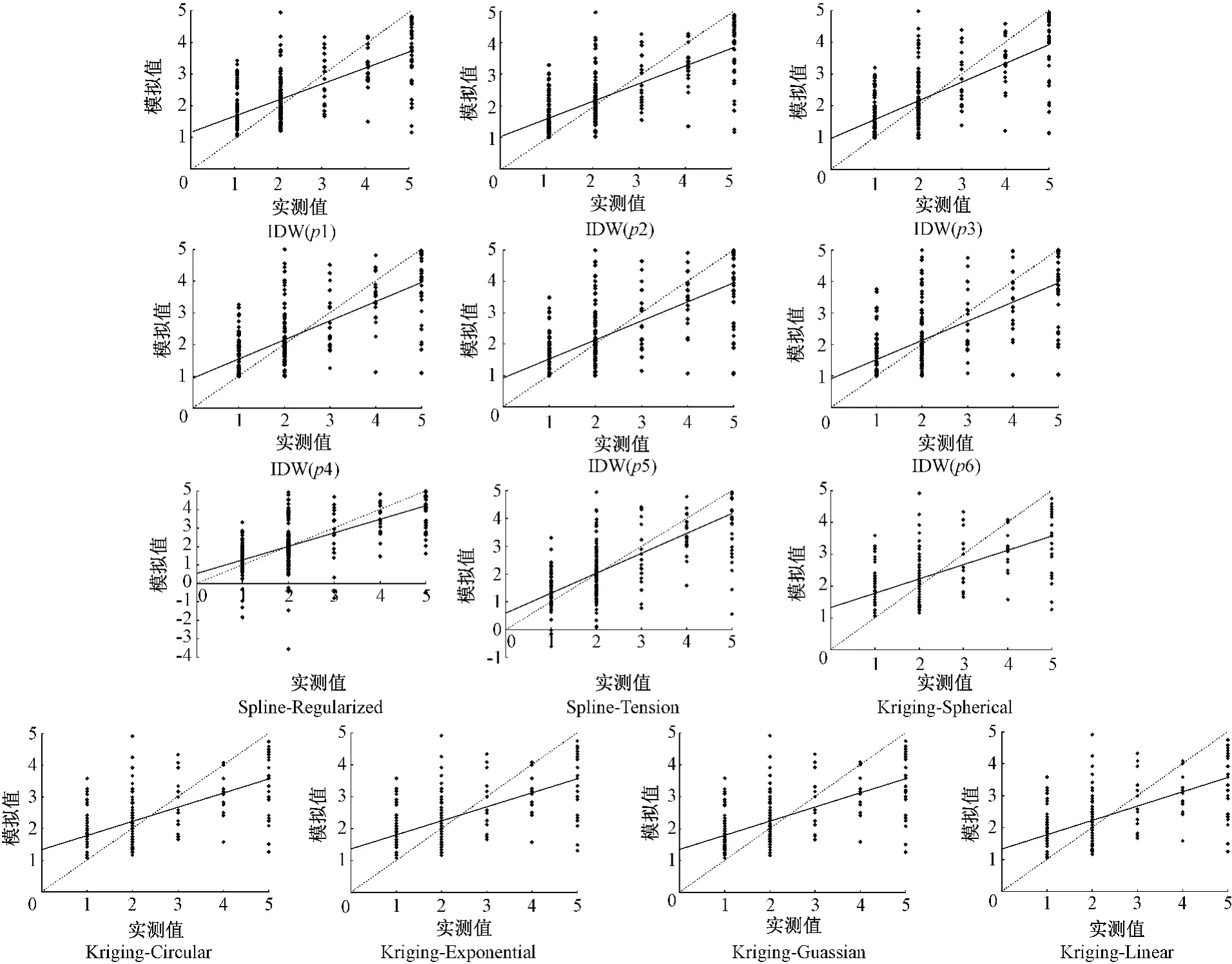
图2 不同插值模型的交叉检验结果散点图

由表1可见，13种插值模型的ME值范围为－0.081 7～0.057 2，从小到大次序为 Spline-Regularized＜Spline-Tension＜IDW(p6)＜IDW(p5)＜IDW(p4)＜IDW(p3)＜IDW(p2)＜IDW(p1)＜Kriging-Linear＜Kriging-Spherical，Kriging-Circular＜Kriging-Guassian＜Kriging-Exponential;MAE值范围为0.625 1～0.853 5，从小到大次序为IDW(p4)＜IDW(p5)＜IDW(p6)＜IDW(p3)＜IDW(p2)＜Spline-Tension＜IDW(p1)＜Kriging-Spherical，Kriging-Circular＜ Kriging-Guassian ＜Kriging-Linear＜Kriging-Exponential＜Spline-Regularized;RMSE值范围为0.934 4～1.216 0，从小到大的次序为IDW(p2)＜Spline-Tension＜IDW(p3)＜IDW(p4)＜IDW(p1)＜IDW(p5)＜IDW(p6)＜ Kriging-Guassian ＜ Kriging-Spherical，Kriging-Circular＜Kriging-Linear＜Kriging-Exponential＜Spline-Regularized;Corr范围为0.643～0.750，从大到小次序为 Spline-Tension＜IDW(p2)＜IDW(p3)＜IDW(p4)＜IDW(p1)＜IDW(p5)＜IDW(p6)＜Spline-Regularized＜Kriging-Guassian ＜ Kriging-Spherical， Kriging-Circular＜Kriging-Linear＜Kriging-Exponential，各插值模型的模拟值和实测值在置信度0.01水平上显著性相关，说明模拟结果与实测结果很吻合，基本能反映海水水质的平面分布规律。

比较各插值模型的模拟值与实测值(图2)。

从线性拟合与最佳拟合效果(图中虚线，1∶1)的偏离度来看，IDW(p=2，3，4，5，6)法和 Spline法的效果优于其他方法，但在Spline法的结果中，个别站位海水水质出现负值，偏离实际情况，说明该模型的适用性相对较差。综合考虑各插值模型的误差及与实际情况的吻合程度，推荐最佳插值模型是IDW(p2)，按RI值偏离最佳插值模型的次序为IDW(p2)＜Spline-Tension＜IDW(p3)＜IDW(p4)＜IDW(p1)＜IDW(p5)＜IDW(p6)＜Kriging-Guassion ＜ Kriging-Spherical，Kriging-Circular＜Kriging-Linear＜Kriging-Exponential＜Spline-Regularized。

3 结论

基于2009年全国近岸海域海水水质监测数据，利用交叉检验法，分析了常用的3种插值算法13种模型的模拟精度，验证了其在近岸海域水质平面分布表征中的适用性，并根据模拟效果提出最优插值模型。

1)插值模型的模拟结果与实测结果具有显著相关性，说明用插值模型能较好地表征海水水质空间分布，其模拟结果可以代表实际监测站位的水质平面分布特征，13种空间插值模型适用于全国近岸海域海水水质的分析和评价。

2)随研究区域和站位设置的不同，适宜的插值模型也不相同。3种插值算法13种模型中，IDW(p2)插值模型最适宜模拟近岸海域水质分布。但该插值模型不能代表不同区域、不同要素的适用性，今后有待于进一步研究不同污染物插值模型的精度。

［1］王业耀，李俊龙，刘方．中国近岸海域环境监测技术路线研究［J］．中国环境监测，2013，29(5):118-123．

［2］BurroughP A， McDonnellR A． Principlesof Geographical Information Systems．Spatial Information Systems and Geostatistics［M］．New York:Oxford University Press，1998:333．

［3］Ramirez-Herrera M，Urrutia-Fucugauchi J．Morphotectonic zones along the coast of the Pacific continentalmargin［J］．Southern Mexico Geomorphology，1999，28:237-250．

［4］Javier B P，Jose L H．Comparing the performance of two spatial interpolation methods for creating a digital bathymetric model of the Yucatan submerged platform［J］．Pan-American Journal of Aquatic Sciences，2007，2(3):247-254．

［5］向运荣，张轶男，刘俊．粤港珠江三角洲区域空气质量分级技术及信息发布方法研究［J］．中国环境监测，2009，25(1):7-10．

［6］曾武涛，刘红卫．珠江三角洲地区空气自动监控网络数据空间模拟适用方法［J］．中国环境监测，2008，24(1):51-54．

［7］陈彦军，李伟铿，张宝春，等．基于GIS的珠三角区域空气质量时空演化分析模型研究［J］．中国环境监测，2012，28(5):136-141．

［8］Klenke M，Schenke H W．A new bathymetric model for the central Fram strait［J］．Marine Geophysical Researches，2002，23:367-378．

［9］Wright D J，Bloomer S H．Bathymetry of the tonga trench and forearc:amap series［J］．Marine Geophysical Researches，2000，21:489-511．

［10］Merino M． Upwelling on the Yucatan Shelf:hydrographic evidence ［J］． JournalofMarine Systems，1997，13:101-121．

［11］GB 3097—1997 海水水质标准［S］．

［12］HJ 442—2008 近岸海域环境监测规范［S］．

［13］中华人民共和国环境保护部．中国近岸海域环境质量公报［R］．北京:环境保护部，2003—2009．

［14］张慧智，史学正．中国土壤温度的空间插值方法比较［J］．地理研究，2008，27(6):1 307-1 329．

［15］Kravchenco A，Bullock D G．A comparative study of interpolation methods for mapping soil properties［J］．Agronomy Journal，1999，13:101-121．

［16］Isaak E H．An Introduction to Applied Geostatistics［M］．New York:Oxford University Press，1989:561．