基于AGNES算法优化BP神经网络和GIS系统的大气污染物浓度预测

姚 宁，马青兰，张 晶，文 印

1．太原理工大学:a．环境科学与工程学院，b．现代科技学院，山西 太原 030024

2．广西大学林学院，广西 南宁 530004

3．亚热带农业生物资源保护与利用国家重点实验室，广西 南宁 530004

近年来，随着国家对大气污染防治的重视，全国城市空气质量总体保持稳定，但以二氧化硫、氮氧化物和颗粒物为主的大气污染依然较为严重［1］，尤其是雾霾现象逐渐引起公众的关注。空气污染对气候、生态系统、土壤以及人体健康带来的危害是巨大的，因此，大气污染物浓度的预测将会成为未来气象预报的重要内容，也会成为未来环境管理和预警的重要参考［2］。

经典的大气污染物浓度预测方法主要依靠以污染物排放源为基础的数学模型，这些数学模型主要研究污染物扩散因子之间的关系，典型的有无界高斯烟流扩散模式、静小风扩散模式、封闭性扩散模式、线源扩散模式、面源扩散模式等［3］。随着模糊数学、系统工程学、GIS空间分析在环境科学领域的深入，以及现代人工智能技术的不断完善，出现了一系列基于环境因子的新型预测方法，如模糊识别法、人工神经网络预测、GIS空间插值预测［4］等。

本研究建立污染物浓度与影响因子之间的BP神经网络，对城市中各监测点位的次日大气污染物浓度进行预测，并运用GIS的插值分析进行污染物空间分布预测，其中BP神经网络的输入向量采用AGNES算法进行处理，总体结构如图1所示。

图1 系统总体结构

1 构建大气污染物浓度的优化BP神经网络模型

1.1 神经网络模型架构

BP(Back-Propagation)神经网络是目前使用最广泛的人工神经网络，对于非线性关系可以做出很好的模拟和预测。该网络是基于误差逆传播算法训练的多层前馈网络［5］，BP神经网络的学习特点是误差反向传播。如图2所示，根据输出节点的误差反馈，调整输入节点的权重系数，以达到最佳的神经网络模型［6］。

研究表明，气温、湿度、降水量、气压、风速等气象因素是大气污染物扩散的主要影响因子［7］，当天的污染物浓度还与前5天的历史浓度有着比较强的非线性关系［8］。本研究采用气温、湿度、降水量、换算后成海平面气压的大气压强、风速和前5天的污染物浓度等10个参数作为神经网络的输入数据，用X=［x1，x2…x10］表示，输入层神经元个数为10。根据万能逼近定理［9］，存在一个可以以任意精度逼近任意连续函数的高斯型模糊逻辑系统，所以对于3层BP神经网络来说，只要隐藏层的神经元个数足够多，是能够做出高精度预测的。设隐藏层输出向量为 Y=［y1，y2…yn］，神经元个数为n，隐藏层输入函数为f1，输出层为监测点位的污染物浓度值，神经元个数为1，输出函数为f2，输出值设为a，ω为各层神经元之间的连接权重系数，θ为各神经元的阈值。隐藏层的输出为式中:k为输出层神经元的下标，本文中k=1。

用MATLAB中的newff函数创建一个反射传播算法的BP神经网络，隐藏层神经元个数的确定根据经验公式［10］，取3 ～14。

图2 BP神经网络拓扑结构示意图

1.2 数据归一化

数据归一化是为了避免因离散值存在而造成的数据模型不收敛的情况［11］，采用 MATLAB软件中的premnmx函数进行数据归一化处理，模型输出值用postmnmx函数进行反归一化，以得到相应量纲的数据。

1.3 模型训练

采用研究城市最近200天的10个影响参数和对应该日污染物浓度值(来源于当地环境保护局空气质量发布系统)作为输入矩阵对BP神经网络进行训练，训练函数采用traingdm函数，训练完成即可进行预测仿真。

1.4 AGNES算法优化训练数据

AGNES(Agglomerative Nesting)是凝聚的层次聚类算法［12］，首先找出对象间欧式距离最小的两个簇，合并为一个新的簇，然后将其包含在下一次的聚类对象中，继续寻找合并，直到所有的簇都合并成为一个最大的簇，建立层次聚类表，按照条件选出最佳聚类方案。将归一化之后的训练输入数据进行AGNES算法聚类，然后找出每一类中偏差最大的一组数据(某一天的10个参数)剔除，这样做有助于减少个别离散值对BP神经网络带来的影响，对提高网络的精确性有帮助。

2 基于GIS的污染物空间分布预测

GIS的空间插值分析主要是从有限个点的观测数据中找到一组函数关系，并根据这组函数关系推求出更多点的值或是整个区域值的分布，表1列出了ArcGIS中5种插值方法的比较［13－16］。根据环保部门发布的各国控监测点位污染物浓度和气象预报，结合BP神经网络和GIS空间差值法，可以实现污染物的分布预测。由于自动监测技术有限，各城市检测点位普遍不多［17］，所以采用ArcGIS中的Kriging插值法。

表1 ArcGIS中5种插值方法的比较

3 预测实例

3.1 BP神经网络预测污染物浓度

采用太原市环保局AQI发布系统公布的SO2、PM10日均值浓度(2013年10月28日—2014年5月17日，第N天到第(N+4)天的浓度作为(N+5)天的参数)和中央气象台发布的太原市气象数据(2013年11月2日—2014年5月22日，包括平均温度、平均湿度、降水量、海平面气压、平均风速)作为研究对象，把这些数据按照1∶1分为训练集和验证集，训练集数据经过归一化、AGNES算法聚类和剔除离散值，可以作为BP神经网络的训练矩阵和目标矩阵，设置最大训练次数为90 000 次，计算精度 10－2，速率为10－2。

试验结果显示，预测SO2、PM10浓度的BP神经网络训练效果均较好(图3)。

图3 预测SO2、PM10的BP神经网络训练效果

将这两种污染物的验证集输入训练好的神经网络进行仿真预测，把预测结果(反归一化前)和实际污染物浓度(归一化后)做相关性分析，如图4、图5所示。结果表明，预测结果与实际浓度显著相关。

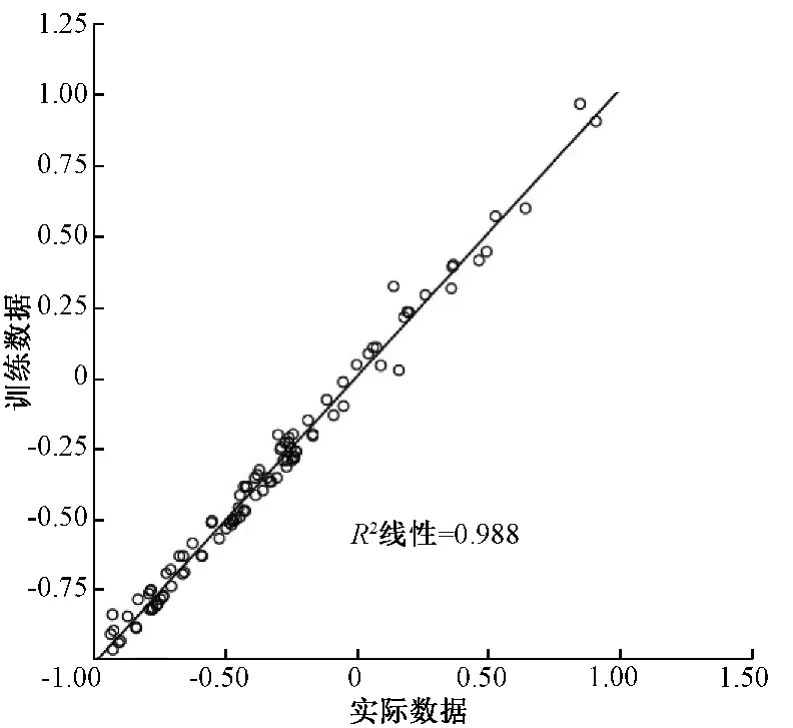
图4 SO2预测浓度与实际浓度的相关性

图5 PM10预测浓度与实际浓度的相关性

3.2 GIS空间插值分析预测污染物的空间分布

运用上述BP神经网络，预测2014年5月27日太原南寨、涧河、尖草坪、桃园、坞城、小店、金胜、晋源8个监测点位SO2和PM10的浓度值。使用ArcGIS的坐标转换功能，将上述8个点位导入图层(北京54坐标系)，创建点文件，以污染物浓度预测值作为Z值字段，对文件进行正态分布分析、协方差分析、空间相关性分析，导出Kriging插值分析图，把太原市区行政图的栅格文件导入作为对照。

两种污染物浓度趋势大体都为从南向北增大，这主要是由于该区域内国控大气污染企业的分布大体呈现北密南疏的趋势，污染物浓度最高的区域为市中心，生活污染源和交通线源污染对其浓度的贡献不容忽视，加之太原西、北、东三面环山的地形特点，使得太原地区的空气常处于沉积、滞留状态［18］，污染物的分布如图6、图7所示。

图6 SO2浓度分布预测图(μg/m3)

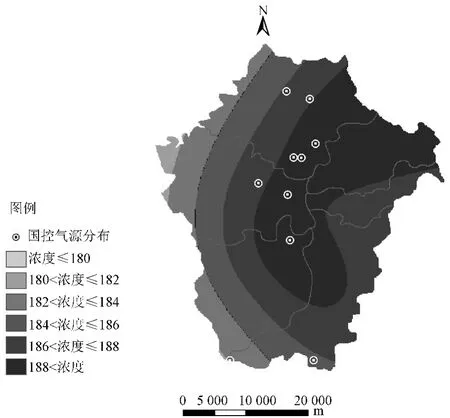
图7 PM10浓度分布预测图(μg/m3)

为了进一步评价污染物分布情况，笔者在该图上标注出区域内所有国控大气污染重点企业，并对污染物分布和国控企业分布做了空间相关性分析。结果表明，两种污染物的分布预测与国控企业分布显著相关，Pearson相关系数分别为0.969、0.949。

4 结论

1)基于AGNES算法优化的BP神经网络，可以减少个别离散值对BP神经网络带来的影响，将输入数据分为训练集和验证集，能够较好地反映出BP神经网络的训练效果;把气象数据和污染物浓度历史数据共同作为影响因子，可以更加真实地反映出污染物浓度的时空变化趋势，为大气环境质量预测和预警提供有效参考。

2)通过对太原市大气污染物浓度的预测可知，试验所建立的AGNES优化BP神经网络基本上可以预测出污染物浓度，对SO2和PM10浓度的预测较为准确。

3)通过BP神经网络预测各监测位点的污染物浓度，结合GIS空间插值分析可以绘制出污染物分布预测图，可以对城市大气污染物的分布作出预测，为区域环境规划和管理提供科学依据。由于影响大气污染物扩散的因素还包括大气稳定度、实际地形地貌、建筑物阻挡、建筑施工等，所以该实验方法只能对分布趋势做大致预测，不能体现局部细节。

［1］2013 中国环境状况公报［R］．中华人民共和国环境保护部，2014-5-27．

［2］雷蕾，秦侠，姚小丽．人工神经网络在环境科学中的应用［J］．环境研究与监测，2007，20(1):50-52，56．

［3］马太玲，张江山．环境影响评价［M］．武汉:华中科技大学出版社，2009.08:116-117．

［4］Corw in D L，Wagenet R J．Application of GIS to the modeling of nonpoint source pollutants in the Vadose zone:a conference overview ［J］． Journal of Environmental Quality，1996，25:403-411．

［5］BaawainM S，AlSerihi A S．Systematic approach for the prediction of ground-level air pollution(around an Industrial Port)using an Artificial Neural Network［J］．Aerosol Air Quality Research，2014，14(1):124-134．

［6］Qimeng W，Ming W．A mathematical expression for air ESD current waveform using BP neural network［J］．Journal of Ekectrostatics，2013，71(2):125-129．

［7］闫妍，张云鹏，李铠月，等．基于BP神经网络的西安环境空气质量的预测［J］．电子设计工程，2013，21(21):54-57．

［8］欧阳钧，王爱枝．基于Matlab的BP神经网络在大气污染物浓度预测中的应用［J］．环境科学与管理，2009，34(11):176-180．

［9］李士勇，李妍．智能优化算法原理与应用［M］．哈尔滨:哈尔滨工业大学出版社，2012:13-17．

［10］徐明德，阎正坤，朱秋丽，等．基于BP神经网络－隶属度的河流黑臭评价研究［J］．数学的实践与认识，2012，42(17):55-61．

［11］Iliadis L，Jayne C．Engineering applications of neural networks［M］．London:Springer，2011:20-24．

［12］许国根．模式识别与智能计算的 MATLAB实现［M］．北京:北京航空航天大学出版社，2012:24-25．

［13］BhattaC S，Mitra，P，Ghosh SK．Spatial interpolation to predict missing attributes in GIS using semantic kriging［J］．Ieee Transactions on Geoscience And Remote Sensing，2014，52(8):4771-4780．

［14］GulerM，Kara T．A comparison of different interpolation techniques used in mapping monthly precipitation in northern turkey［J］．Fresenius Environmental Bulletin，2014，23(2):341-347．

［15］El-Hoz M，Mohsen A，Iaaly A．Assessing groundwater quality in a coastal area using the GIS technique［J］．Desalination and Water Treatment，2014，52(10):1 980-1 989．

［16］Richard L，Glenn G．An interpolation approach for fitting computationally intensive models［J］．Cognitive Systems Research，2014，29-30:53-65．

［17］国家环境监测“十二五”规划［R］．北京:中华人民共和国环保部，2011．

［18］李艳红，周晋红，张春梅．太原市大气污染形成原因初探［J］．山西煤炭科技，2006，11:31-32，43．