基于多目标驱动优化的平面磨床床身结构设计

王毅，宋鹍，杨鸿，张峰

(重庆理工大学机械工程学院，重庆400054)

0 前言

多目标驱动优化理论发展十分迅速，已经被广泛的应用于机械产品设计［1］。但是，其各种优化理论相对复杂［2］，对研发人员数学素养要求较高，对于一般企业很难将其应用到实际的产品设计中。作为CAE领域的佼佼者，ANSYS Workbench 协同仿真平台集成了多目标优化设计算法，可以轻松地对产品进行自动优化设计［3］。但是，现阶段仍然只是使用ANSYS 对建好的三维模型进行相关分析，而后根据分析结果人为的进行优化处理［4］。虽然这个过程已经大大减轻了工作量，但是仍没有完全发挥出ANSYS Workbench软件的优势。目前，磨床床身的设计仍然是根据经验进行［5］。磨床的床身对于磨床的性能有着重大的影响，需要其既有足够的强度又希望其质量轻便于移动安装，同时还要兼顾其动态特性［7］。通过ANSYS Workbench 软件的多目标驱动优化程序，可以解决对机床床身多目标需求的问题［8］。下面以某型号数控磨床床身的优化问题为例，来阐释ANSYS Workbench软件的多目标驱动优化程序在产品设计中的应用。

1 磨床床身参数化建模

众所周知，床身是整个磨床的基础，支撑着整个机床的质量，同时又决定着磨床的稳定性。因此，其重要性不言而喻。增加磨床床身的体积与质量以提高磨床的静态与动态特性，从而提高整台磨床的加工精度，然而过大的质量又严重影响着使用者对磨床的搬运安装，又带来了诸多不便。为了解决这个问题，磨床床身往往会布置筋板［9］，这样可以很好地解决质量与稳定性的问题。但是，往往床身依然占磨床整机质量的一半以上［10］。对于筋板的设计，往往凭设计者的直觉和经验，这样设计出来的磨床床身并不是最优。图1 为机床床身。

图1 机床床身筋板

某型号数控磨床的床身为T 型的铸造结构，根据该型号磨床的具体参数使用Pro/E 软件对该磨床床身进行三维建模，并根据有限元分析相关要求［11］，对模型进行简化。最终的磨床床身三维模型如图2 所示。在进行三维建模时，着重对其筋板的厚度进行了参数化设置，以便在将其导入ANSYS Workbench 软件进行优化时，能够识别其厚度变量，为后面的优化设计做准备。

图2 简化后的磨床床身

2 磨床床身优化分析

2.1 基于多目标驱动优化的目的

一台成型的数控磨床，其外观尺寸已经相对固定，床身的外形尺寸也由该数控磨床的加工参数决定，因此去大范围的改变已有的外形尺寸是不现实的。文中优化的目的就是为了在不改变床身整体尺寸、筋板布置方案的前提下，通过优化其筋板厚度，来满足床身质量最小，同时兼顾其静态动态性能的设计要求。

对于优化目的，抽象为数学关系式可以表示为:

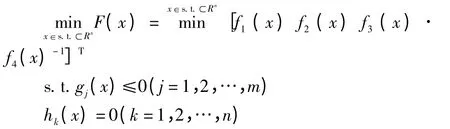
这里f1(x)为质量，f2(x)为应力，f3(x)为变形，f4(x)为一阶固有频率，均为变量x (筋板厚度)的函数。其中约束条件gi(x)和hk(x)应满足工程实际，这里不再特意说明。

若求上式的有效解［12］，通过工程人员编程计算求解是很有难度的。因此，借助Ansys Workbench 软件进行求解。

2.2 基于多目标驱动优化的过程

在对模型进行多目标驱动优化时，应先对模型进行有限元分析。由该型号平面磨床的参数可知，磨床通过其床身的8 个地脚螺栓固定，最大加工工件质量2 000 kg。这就为磨床的有限元分析提供了边界条件。根据已知的边界条件，使用Ansys Workbench 软件对磨床床身进行分析。当筋板厚度取30 mm 时，床身的等效应力云图如图3 所示。

图3 磨床床身等效应力云图

通过分析可知，磨床床身的等效应力并不大，远远低于其材料的许用应力。在静态特性满足条件的情况下，着重分析其动态特性。在对床身的动态特性分析时，重点关注其模态特性［11］。对于模态分析，因为一阶模态频率最低，对于实际指导意义更大［12］，同时为了节约软件资源，提高运行速度，因此只计算床身的一阶模态。

该磨床床身的一阶模态的振型如图4 所示，为沿一方向摆动，此时的共振频率为662.18 Hz。

图4 床身一阶阵型

在完成静态分析与模态分析，就可以进行优化设计了。在优化设计之前，需要把相关输入输出量进行参数化设置。依据设计目标，这里列出相关参数，如表1 所示。

表1 相关参数

Ansys Workbench 提供了完善的设计流程，通过拖动不同的分析模块，并使之数据共享就可以完成一个完整的分析过程。对于多目标优化过程，其在Ansys Workbench 中的分析流程如图5 所示。

图5 分析优化流程

根据软件要求，对输入参数筋板厚度的变化范围进行设定，令筋板厚度DS_t∈(20，40)mm。优化程序将输入参数(筋板厚度)平均分为10 组进行试验，并记录每组实验的输出参数。

2.3 基于多目标驱动优化的结果处理与分析

在得到每组试验结果后，需要对结果进行处理，确定每个变量的影响权重。如表2 所示。

表2 确定变量优化结果及影响权重

图6 输入参数对输出参数灵敏度影响

图7 试验结果及最优选择

确定每个变量的重要程度后，程序会给出相应的曲线。如图6 所示，是输出参数与输入参数之间的灵敏度关系。通过图6 可以看出，筋板厚度的变化与整体质量的灵敏度最高，及对质量影响最大。与应力灵敏度最低，及对应力影响最小。图7 为试验结果以及程序推荐的最优化选择。通过图7 可以看出，程序进行了10 次试验，并且推荐第5、第6 和第10 次试验作为参考选项。推荐的试验参数如表3 所示。

表3 推荐试验组数及结果

3 结论

针对该型号数控磨床床身进行的优化分析主要是优化其床身的筋板厚度。通过Ansys Workbench 软件的多目标驱动优化功能，得出此型号数控磨床床身筋板的最优厚度为30 mm。此文旨在通过优化该数控磨床床身筋板厚度，除了为设计此型号数控磨床提供参考依据，更希望在机械设计中使用Ansys Workbench软件进行多目标驱动优化。通过此种方法，可以大大提高产品设计效率，降低设计成本。

［1］雷宇晓，平面磨床有限元分析与优化［D］．广西:广西大学，2006．

［2］储开宇，杜必强．现代机床设计思想及其发展［J］．水利电力机械，1999，4(2):18－20．

［3］郭媛美，岳崇勤，丁晓红，等．基于ANSYS Workbench 的外圆磨床的有限元分析及优化［J］．机械设计与制造，2010(1):181－182．

［4］陈杰．运用ANSYS Workbench 快速优化设计［C］．安世亚太用户年会论文．2006．

［5］苏渤，王永泉，朱祥，等．基于有限元分析的机床结构优化设计［J］．精密制造与自动化，2011(4):30－34．

［6］贺兵，黄红武，宓海青，等．基于ANSYS 的超高速平面磨床结构优化设计［J］．机械，2004，31(1):7－9．

［7］李晓燕，钱炜，韩红俊．平面磨床床身的三维有限元分析［J］．机械设计与制造工程，2002，31(2):26－29．

［8］黄红武，赵小青，宓海青，等．基于有限元的超高速平面磨床整机动力学建模及模态分析［J］．湖南大学学报，2005，32(4):39－42．

［9］应鸿烈，杨绍荣．平面磨床床身结构分析与优化设计［J］．设计与制造，2012(1):87－89．

［10］郭春星，丁晓红，郭媛美，等．磨床床身结构优化设计［J］．机械设计与研究，2009，25(5):104－107．

［11］王艳辉，伍建国，缪建成，等．精密机床床身结构参数的优化设计［J］．机械设计与研究，2003，19(6):53－55．