基于嵌入式PC的机器人运动控制系统设计

赵彬，张艳荣，高宏力，孔德松，黄晓蓉

(西南交通大学机械工程学院，四川成都610031)

0 前言

随着机器人技术的不断发展，机器人在许多行业得到了广泛的应用。目前机器人电控系统多采用多重主从结构的控制方案。这种结构由于单个芯片的处理能力有限，位置检测、电机驱动、路径规划等不同的任务需要不同的控制单元处理，系统结构复杂，且采用这种方案的机器人在复杂电磁环境的工业环境中，其稳定性和可靠性难以保证。

文献［1］ 采用了ARM7 + AVR 单片机的结构，系统结构复杂，精度不高。文献［2］ 基于嵌入式PC/104 的控制系统，实时性还有待提高。文中设计的三轮全向移动机器人控制系统，采用基于PC +现场总线+ 分布式I/O 的体系结构，硬件结构简单紧凑。嵌入式PC 的高速运算能力和软PLC 的高优先级，保障了程序的执行效率和系统的实时性。

1 三轮全向驱动系统的运动学模型

三轮全向驱动结构与四轮结构和两轮差动的结构相比，具有运动速度快、转向灵活以及在平面上的自由度高等特点，在有限空间的环境中运动时，具有更小的转弯半径和更灵活的路径选择，因此文中选用了三轮全向驱动的结构。

三轮全向驱动系统的驱动轮由3 个质量和大小均一致的全向轮构成，任意两轴之间的夹角θ =120°，轮子半径为r。建立如图1 所示的世界坐标系XOY，以机器人的中心Q 为原点建立机器人坐标系xQy，各轮中心到Q 的距离均为L。

图1 三轮全向驱动系统示意图

设v1、v2、v3分别为3 个全向轮的线速度，Vx、Vy分别为机器人在x、y 方向的分速度，各轮速度、加速度与机器人中心的速度、加速度对应关系见公式(1)、(2)［3］。

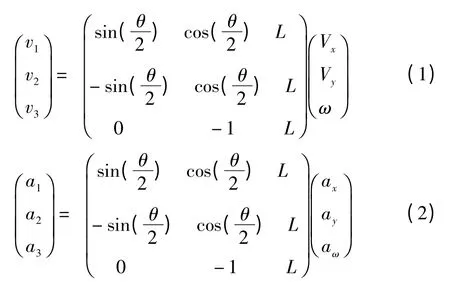
又设(x，y)为机器人的中心Q 在世界坐标系XOY 内的坐标，α 为机器人坐标系x 方向和世界坐标系X 方向的夹角，令ξ = (x y α)T，则有式 (3)、(4)的变换关系［3］:

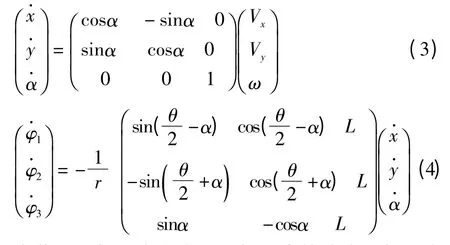
由此得到机器人在世界坐标系中的速度和机器人3 个全向轮速度的转换关系。

2 运动控制硬件系统设计

所设计的基于嵌入式PC 的三轮全向移动机器人控制系统，采用BECKHOFF 的CX1030 嵌入式PC 作为控制器，CPU 模块、RS232 串口模块以及具有EBUS 接口的电源模块通过标准的PC/104 接口相互连接，运行的操作系统为Windows CE。CX1030 后端连接EtherCAT 总线的数字量输入输出模块、传感器信号采集模块以及电机驱动模块等。3 个小型直流伺服电机经减速器传动后分别驱动3 个双排式全向轮。由于控制器的运算速度足够快，在控制器操作系统里安装TwinCAT 软件后虚拟一个软PLC，数据采集和处理、路径规划和运动控制这3 个任务均由软PLC 来完成。系统的硬件结构如图2 所示。

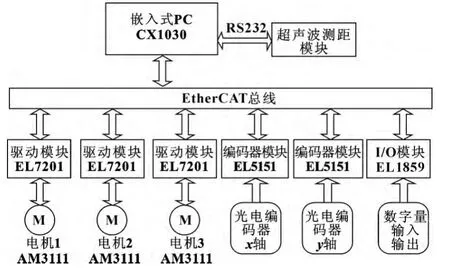
图2 硬件系统框图

机器人在按照预定指令行走的过程中，x 轴和y轴的编码器不间断检测行进位移，信号经采集后通过EtherCAT 总线将结果反馈给控制器。超声波测距模块和光电开关用于知周围环境。在机器人活动范围的地板上，关键位置涂有与地板不同的颜色，光电开关发出调制光照射在地板上，传感器接收地面的反射光并根据信号的强弱来区分地面不同区域，其输出的数字量信号通过I/O 模块采集经EtherCAT 总线传输至控制器。普通的超声波测距模块需要给一个激励信号后返回一个测量值，其工作过程复杂耗时，设计采用带有RS232 串口的超声波测距模块，该模块自身会不断测量距离，通过RS232 串口实时将测得的距离值传送给控制器。控制器依据这些环境信息和编码器位置信息综合决策，更新下一阶段的路径规划指令。

在系统中，伺服电机的性能对机器人行走路径(不考虑地面摩擦)影响很大，特别是在有较大的负载扰动时，电机能否迅速的减小速度偏差并稳定，直接影响到机器人的姿态是否稳定和路径跟踪是否准确。设计采用BECKHOFF 的AM3111 直流伺服电机，由EL7201 伺服驱动模块驱动，电机的速度环使用PI控制，其能迅速减小电机输出转速的偏差且快速趋于稳定。旋转变压器作为电机的反馈测量元件，测量精度高，且能耐受较大的振动冲击，为机器人在复杂环境中的应用提供保障。用试凑法调整电机的PI 控制器参数，当K=200，Tn=0.1 时，电机具有较好的性能。测试时，在第9 s 附近加入负载扰动，观测电机的转速变化，结果如图3 所示，电机能迅速地减小速度偏差并稳定，满足机器人的应用要求。

图3 电机测试结果

3 软件控制算法

机器人在移动的过程中是一个非线性的时变系统，传统的PID 控制高度依赖被控对象的精确模型，由于机器人制造安装过程中产生了误差，使用过程中又有负载扰动，难以得到整个系统的精确模型，因此在机器人在轨迹跟踪时取得的控制效果与预期相比并不理想，而模糊控制本身属于非线性控制方法，对被控对象的数学模型依赖程度不高，所以使用模糊控制器设计路径规划系统［4－10］。

模糊控制器设计为双输入、双输出的结构，输入为机器人当前位置与目标位置的距离D，当前姿态与世界坐标系的夹角α，输出为机器人的线速度v 和角速度ω。输入端D 的论域为［0，2 000 mm］，夹角α的论域为［－π，π］;输出端v 的论域为［0 mm/s，1 000 mm/s］，ω 的论域为［－4 rad/s，4 rad/s］。输入变量D 和输出变量v 的模糊集定义为 {ZO，VS，SM，ME，BG，VB，EB}，输入变量α 和输出变量ω的模糊集定义为 {NB，NM，NS，ZO，PS，PM，PB}，4 个变量的隶属度函数均为三角函数。模糊控制规则如表1 所示。文中采用最大－最小模糊推理方法，解模糊采用重心法。

表1 机器人的线速度v 和角速度ω 的模糊控制规则表

对控制系统建模，Matlab 仿真框图如图4 所示，设机器人从起点位置跟踪一个固定点(500，100)，位置计算模块计算出当前位置的与目标点的距离和夹角，将计算结果作为模糊控制器的输入，经过模糊推理和解模糊后，输出机器人线速度和角速度指令，驱动模块对给定的线速度和角速度解算为3 个驱动电机的速度，并将行进的位置坐标反馈给位置计算模块。机器人仿真运行的轨迹如图5 所示，运行轨迹平滑，没有出现剧烈震荡或者失稳的现象。

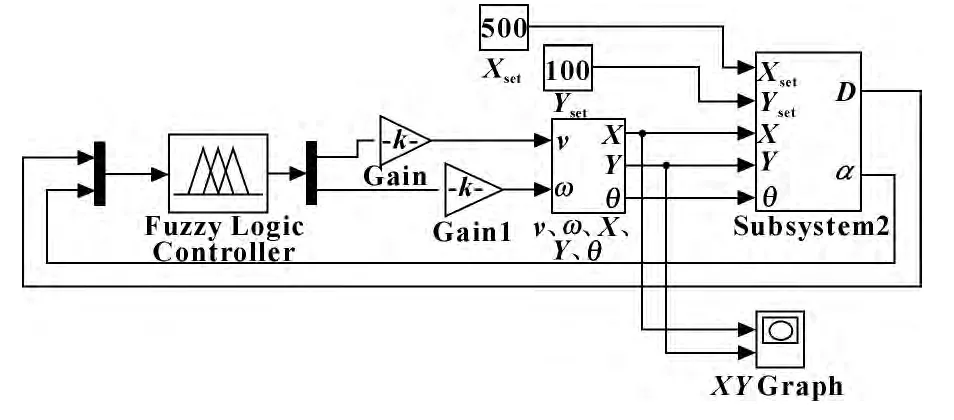
图4 仿真模型

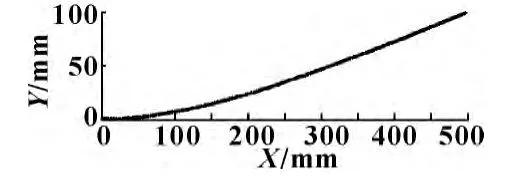
图5 仿真结果

环境感知、路径规划和电机驱动是本系统的3 个主要任务，其对实时性的要求也不同。控制器内部的软PLC 设置最多4 个任务，各个任务独立运行，根据不同任务的重要性，可设置其扫描周期和优先级。将机器人的环境感知、路径规划和电机驱动分别以设置成独立运行的任务，如图6 所示，环境感知程序设置最高的优先级，扫描周期10 ms，路径规划程序和电机驱动程序的优先级依次降低，扫描周期均设置为20 ms，保证实时性的同时节省了系统资源。各个任务之间通过全局变量进行数据交换。

图6 任务分配

4 实验结果

将机器人置于世界坐标系XOY 的原点，其坐标系与世界坐标系的夹角α =0，拟定路径点的坐标(Xset，Yset)∈{(1 000，800)，(1 500，1 500)，(2 000，1 700)， (3 000，1 700)，(4 000，100)}，实验结果如图7 所示，图中的实线是在仿真环境里生成的预计路径，虚线是实际路径。

实验时，机器人在跟踪较远距离的点时速度快，在跟踪较近的点时速度较慢。由于机器人自身的惯性较大，且与地面的摩擦力小，机器人的实际行进路径与预计的路径相比有偏移，对设定路径点的重合度较好，定点精度12 mm，考虑到机器人自身体积较大，该精度可以满足应用要求。在实验中还发现，如果设定机器人的行走最大速度值过大，在跟踪比较密集的路径点时容易产生失稳震荡的现象，此时应减小速度增益。

图7 路径跟踪的轨迹

5 结束语

将嵌入式PC 应用在三轮全向机器人控制系统中，与常见的主从多级结构的电控系统相比，该系统所采用的PC +现场总线+分布式I/O 的体系结构使系统硬件结构更简单;软件中采用了模糊控制算法，系统的鲁棒性佳;不同功能的程序在软PLC 里划分为单独的任务执行，系统的运行效率高。由于嵌入式PC 的运算速度快，数据采集和处理能力强，系统还可增加其他类型的传感器，如激光雷达、图像采集设备等，对环境建模更加精确，路径规划更合理。

［1］王志龙，赵剡，杨辉，等．全向移动机器人电控系统设计［J］．自动化与仪表，2012，27(9):6－10．

［2］张跃进，展爱云，刘觉夫．基于PC/104 嵌入式越障机器人系统的设计［J］．微计算机信息，2008，24(9－2):13－15．

［3］季秀才．RoboCup 小型组机器人运动控制研究［D］．长沙:国防科技大学，2003:51－57．

［4］刘荣．自动机器人轨迹控制系统及相关算法研究［D］．成都:电子科技大学，2008:50－60．

［5］王淑坤，王宏健，吕琼莹．全向驱动电动轮系统研究［J］．机械设计，2012，29(10):93－96．

［6］AICARDI M，CASALINO G，BICCHI A，et al．Closed Loop Steering of Unicycle-like Vehicles Via Lapunov Techniques［J］．In IEEE Robotics ＆Automation Magazine，1995，2(1):27－35．

［7］INDIVERI，Giovanni．Swedish Wheeled Omnidirectional Mobile Robots:Kinematics Analysis and Control［J］．IEEE Transactions on Robotics，2009，25(1):164－171．

［8］李艳，林廷圻，黄玉美，等．基于神经网络的3 自由度移动机器人跟踪方法研究［J］．西安交通大学学报，2003，7(37):711－714．

［9］薛定宇，陈阳泉．基于Matlab/Simulink 的系统仿真技术与应用［M］．北京:清华大学出版社，2002．

［10］KUMAR-NAGY Tomas，ANDREA Rafaela D，GANGLY Puritan．Near-optimal Dynamic Trajectory Generation and Control of an Omni-directional Vehicle［J］．Robotics and Autonomous Systems，2004，46:47－64．