连杆参数误差对机器人精度可靠性的影响

张晓瑾，胡斯乐，林粤科，梅雪川

(1. 广州机械科学研究院有限公司，广东广州510700;2. 广汽本田汽车有限公司，广东广州510700)

0 前言

影响串联机器人末端执行器静态位姿精度的误差源有很多，包括外部环境引起的误差和内部机构参数误差。外部误差主要包括有周围环境的温度、邻近设备的振动、电网电压波动、空气湿度与污染、操作者的干预等;内部误差主要包括几何参数误差、受力变形、热变形、摩擦力、振动等。

考虑到大部分机器人大多是室内车间作业，因而外部误差影响不大，以焊接机器人为例，其主要是低速轻负载作业，受力变形、热变形、摩擦、振动引起的误差也很小，其主要误差来源还是几何参数误差，该误差占工业机器人所有误差的80%以上。

所谓几何参数误差，即表示在运动学模型中，几何参数的名义值与真实值的偏差。目前，机器人末端执行器位置的静态精度误差分析大都采用传递矩阵法或矢量法，且在机器人各构件参数误差及各关节的运动变量确定的条件下，研究机器人末端执行器的位姿精度误差变化规律［1－4］。静态精度误差分析时假设机器人各构件为质量忽略不计的理想刚体。在这种假设下，引起机器人末端执行器位姿精度误差的主要因素为结构参数和运动变量误差。本章采用传递矩阵法研究由静态误差引起的机器人末端位姿精度误差，建立机器人静态位姿精度误差模型，用一个统计学参数来评价机器人的精度水平，即以可靠度为指标对串联机器人末端执行器运动精度误差进行研究。

1 串联机器人的运动学描述及其静态位姿误差

串联机器人是用关节将系列连杆连接在一起而构成的。在对机器人进行运动学和动力学分析时多采用D-H 法来建立机器人坐标系［5－6］，并利用改进的D-H模型［7］，建立坐标系{N}相对于坐标系{0}的变换矩阵为［8］:

其中:

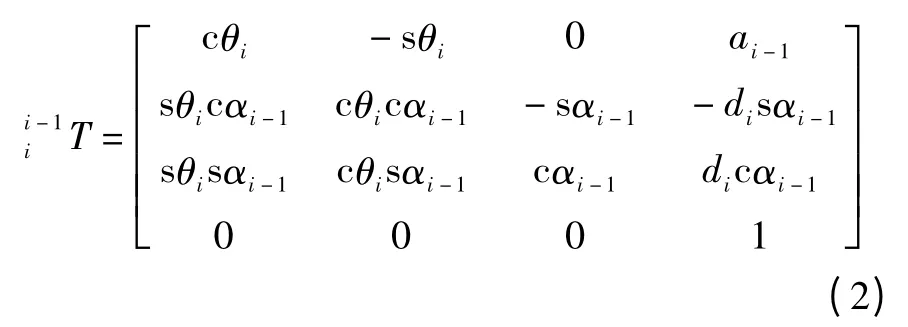
串联机器人末端执行器的位姿精度受多方面因素影响，这些影响均会使连杆关节变量和关节参数产生误差，即:Δθi、Δdi、Δai、Δαi，从而使机器人末端执行器位姿产生误差。从误差理论与传递情况分析，机器人末端执行器的位姿误差与各组成连杆的运动变量和结构参数误差之间存在着函数关系，因此，研究串联机器人的位姿误差也就可归结为其函数误差的研究。

针对实际情况，式(1)中θi、di、ai、αi均为随机变量，利用微小位移合成法［9］，首先确定机器人在某一姿态下的误差阵，即ΔT 为:

其中，∂T/∂θi、∂T/∂di、∂T/∂ai、∂T/∂αi为连杆转角θi、连杆距离di、连杆长度ai、连杆扭转角αi的误差传递矩阵，假定Vij(j =1，2，3，4)相应地代表机器人各组成连杆的关节变量和结构参数di、θi、ai和αi，则机器人末端执行器的位置广义坐标对于各组成连杆的关节变量和结构参数的偏导数为:

当姿态广义坐标取为X-Y-Z 固定坐标系(α，β，γ)时，末端执行器姿态对于各组成连杆的关节变量和结构参数di、θi、ai和αi求偏导数，即:

2 应用蒙特卡洛法分析串联机器人静态位姿精度可靠性

蒙特卡洛方法［10］又称随机抽样方法，利用随机数进行统计实验，以求得的统计特征值 (如均值、方差、概率等)作为待解问题的数值解。随着现代计算技术的飞速发展，蒙特卡洛方法越来越广泛地应用到各种科学研究中。误差的蒙特卡洛模拟方法，就是对具有不同的分布特性的原始误差随机量进行抽样，按照误差模型计算和统计误差值分布的一种方法。文中主要对引起串联机器人静态位姿误差的几何参数误差进行模拟和分析。串联机器人各几何参数误差具有随机性，故其引起的末端执行器位姿误差亦具有随机性。

将误差的抽样值代入末端执行器的位姿误差数学模型，获得末端执行器位姿误差的抽样值，采用末端执行器的位置误差落在半径为R 的误差球体内的概率和姿态误差小于给定误差T 的概率，来量化分析手部位姿误差，用精度可靠度表示。其中，位置与姿态误差分别按如下公式计算:

Pi是在同一位姿对关节变量和结构参数di、θi、ai和αi抽样计算第i 次时所得点位置值，αi、βi和γi是在同一位姿对关节变量和结构参数di、θi、ai和αi抽样计算第i 次时所得的姿态角。Pc、αc、βc和γc为机器人末端执行器理想位姿坐标值。

设位置误差ΔPi和姿态误差Δφi= (Δαi，Δβi，Δγi)T小于给定误差R 和T= (Tα，Tβ，Tγ)T的样本数分别为λP、λφ= (λα，λβ，λγ)T，那么机器人位置误差和姿态误差小于给定误差R 和T 的概率近似等于位姿小于给定误差的样本数除以样本总数λ，即机器人精度可靠度为:

2.1 关节参数对静态位姿精度可靠性影响分析

以五自由度串联机器人进行分析，其连杆参数如表1 所示。

表1 五自由度串联机器人连杆及关节参数

计算时做如下假设:关节转角θi和关节参数di、ai、αi均服从正态分布，其中，关节参数di、ai、αi均值如表1 所示，标准差分别为0.05 mm、0.05 mm、0.5°;关节转角θi标准差为0.5°，现计算各关节从零位转动45°时，机器人末端执行器位姿准确度的可靠度。

应用串联机器人末端执行器坐标系相对于基坐标系的转换矩阵公式，再对5-DOF 串联机器人的4 种随机变量进行105次抽样，代入公式中，就可得机器人末端执行器在θ1=45°，θ2=45°，θ3=105°，θ4=45°，θ5=45°所达点C 处的0T5，分别计算机器人末端执行器位置和姿态误差值。表2 所示为位姿理想值和抽样计算所得样本的数字特征。

各参数误差对欧拉角Δα 均值影响最大。位置误差、姿态误差经χ2拟合优度检验在显著性水平α =0.05 下服从正态分布，各正态分布参数如表2 所示。

表2 机器人末端执行器位姿误差理想值和样本的数字特征

对给定的末端执行器的位置误差球体半径R =3 mm和姿态给定误差T =0.02°，机器人末端执行器的可靠度为:

为便于比较，在其他参数相同的情况下，取关节转角θi和关节参数di、ai、αi均值不变，标准差分别减小5 倍，即依次取表3 所列标准差组合形式，计算串联机器人末端执行器位姿误差可靠度。

表3 各参数均值不变，标准差分别减小5 倍时机器人末端执行器位姿误差样本的数字特征

以机构可靠度为评价指标，由表3 可知，当机器人关节转角θi和关节参数di、ai、αi标准差都减小5倍的情况下，关节转角θi误差标准差的减小，使得机构位置精度可靠性显著提高，其他参数连杆转角αi、连杆长度ai、连杆偏距di误差标准差的减小对机构位置精度可靠性的影响不明显。各参数对末端执行器姿态精度可靠度的影响程度同机构位置精度可靠性。由此可以得出，关节转角θi的误差分布对机器人机构可靠度影响较大，为了提高机器人的可靠度，通过采用精度较高的驱动电机、减小动力传动中的传递误差等措施来控制末端位姿误差。

2.2 各关节对静态位姿精度可靠性影响程度

为分析各关节对串联机器人末端执行器位姿精度可靠性的影响，方便观察结果，在与关节参数对静态位姿精度可靠性影响分析中相同的指令位姿，取对末端执行器位姿精度可靠性影响最大的关节转角θi，改变其分散性，其他参数分布形式不变进行分析。即取各关节标准差σθ1～σθ5分别减小5 倍，研究其对机器人末端执行器位姿精度可靠性的影响，结果如表4所示。

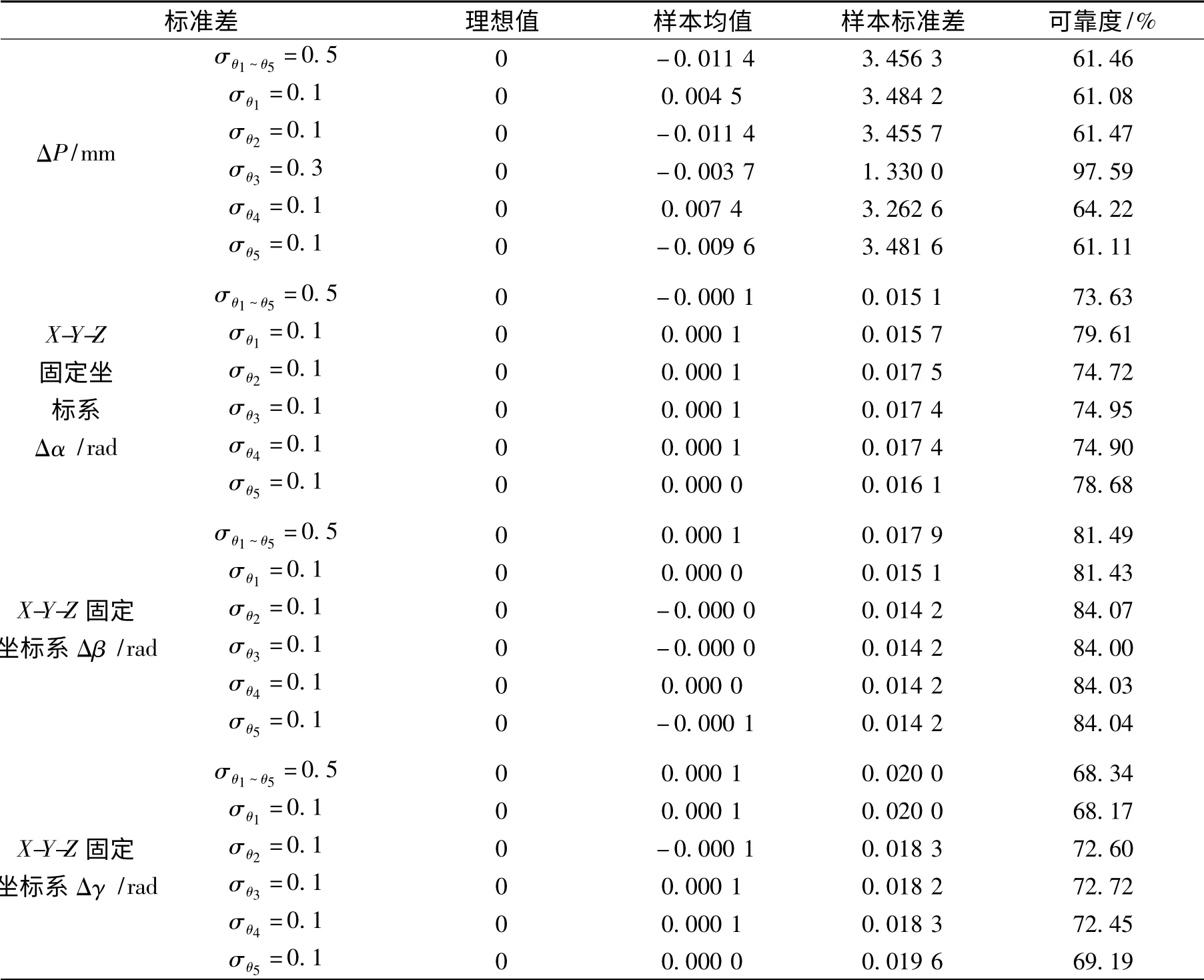
表4 各关节转角均值不变，标准差分别减小5 倍时机器人末端执行器位姿样本的数字特征

由表4 可以看出，当其他3 个连杆参数误差分布不变时，关节1 ～5 的关节转角分别减小5 倍，经蒙特卡洛分析可知，对给定的末端执行器的位置误差球体半径R=3 mm，关节3 处的关节转角误差分布对末端执行器的位置可靠度影响最大，其他关节转角误差分布的改变对姿态可靠度影响不大。因此，可知在要求位置精度时，应特别减小关节3 的关节转角误差值。

3 结论

对由静态误差引起的串联机器人末端位姿精度可靠性做了分析，建立了串联机器人的静态位姿精度误差及精度可靠性模型，并以5 自由度串联机器人为例，采用Monte Carlo 统计模拟方法，计算了串联机器人末端执行器位姿精度误差及可靠性，以精度可靠度为评价指标，关节转角θi的误差对串联机器人末端位姿精度误差的影响比较大，且关节3 处得关节转角误差值对串联机器人末端位姿精度误差尤其重要，因此在设计、安装、使用时，应尽量减小串联机器人各关节转角的误差，对关节3 的关节转角误差更应严格控制。

［1］WU C h．A Kinematic CAD Tool for the Design and Control of a Robot Manipulator ［J］．The International Journal of Robotics Research，1984．16(1):58－67．

［2］KUMAR A，P．S．Analysis of Mechanical Errors in Manipulators［C］//Proc．6thWorld Cong on TMM，1983:960－964．

［3］黄真．机器人手臂误差分析及误差传递函数［C］//15thISIR，1985:873－878．

［4］陈明哲，张启先．工业机器人误差分析［J］．北京航空学院学报，1984(2):11－22．

［5］熊有伦．机器人学［M］．北京:机械工业出版社，1993．

［6］ISO9787-1999．Manipulating Industrial Robots-Coordinate Systems and Motion Nomenclatures 1999［S］．

［7］John J Craig．机器人学导论［M］．3 版．贠，译．北京:机械工业出版社，2011:161．

［8］BRUNO Siciliano，OUSSAMA Khatib．Springer Handbook of Robotics［M］．Springer，2007．

［9］徐卫良，张启先．机器人机构误差分析的微小位移合成法［J］．南京工学院学报，1987，1(6):45－54．

［10］谢里阳，王正，周金宇，等．机械可靠性基本理论与方法［M］．北京:科学出版社，2009:54－70．