某特大跨径拱桥静动载试验分析与评价

耿 泽，孙亚民，裴存栋

(长安大学公路学院，西安 710064)

引言

近年来，随着公路运输压力的不断增加，对设计、在建、在役及技术加固后的桥梁质量要求越来越高，特别是新的设计理论、设计思想、施工技术不断应用到桥梁结构中，桥梁结构越来越复杂，跨径越来越大，对桥梁进行荷载试验，确定其结构的承载能力和使用性能，检测桥梁结构的实际工作状态是否满足设计荷载作用下的工作要求，便显得尤为重要［1］。

拱桥造型优美，承载能力大，主跨200 m以上的特大跨径钢筋混凝土拱桥并不多见，本文以福建省境内某特大跨径钢筋混凝土拱桥为研究对象，建立空间模型，参考已得到的桥梁技术评定结果，分析得出其在静力荷载作用下的控制截面应力和挠度计算值，及主体结构自振频率特性、行车动力响应结果，与实际加载的实测值进行比较，从而评价该桥的健康状况。

1 桥梁概况

该桥设计方案为:5×20 m预应力空心板+1×228.2 m钢筋混凝土箱型拱(主拱净距204.959 m)+3×20 m预应力空心板(全桥桥长405.4 m)，拱轴线采用悬链线，拱轴系数m=1.875，其中主孔采用单箱三室节段预制。桥面横坡2%，桥面总宽10 m，桥面布置:0.5 m(防撞栏杆)+9 m(行车道)+0.5 m(防撞栏杆)。桥梁设计汽车荷载等级为公路—I级。拱上结构跨度布置采用12.66 m、12.68 m两种跨度形式，共布置18孔，桥面系由8片预应力混凝土空心板梁组成，拱座设计为重力式钢筋混凝土实体结构。根据该桥的设计说明，主拱圈、预应力空心板采用C50混凝土，立柱及帽梁等其它拱上建筑采用C30混凝土，弹性模量取Ec=3.45×104MPa。该桥已使用超过5年，通过《公路桥梁技术状况评定标准》(JTG/T H21—2011)对桥梁各部件进行等级评定，该桥评定为3类桥。

2 有限元模型的建立

主桥力学模型采用有限元软件Midas Civil 2012参考设计图纸建立有限元模型。建模时，利用拱建模助手建立拱肋形状，采用空间梁格法模拟桥面板，空心板的铰接缝通过释放梁端约束来模拟，横向虚拟联系梁的截面特性与空心板保持一致，拱脚处固结，立柱与拱肋之间的约束采用主从关系来模拟，盖梁与立柱、桥面板之间的约束采用弹性连接模拟，将车轮荷载作为集中力处理［2］。

各承重构件的计算采用计入普通钢筋的换算截面，全桥共分2181个节点和2588个单元。本文利用Anil K C［3］的对称三角形脉冲力理论，通过软件模拟不同速度的汽车车列，以分析无障碍行车试验，具体模型如图1所示。

图1 拱桥有限元模型

3 试验方案

3.1 静载试验方案

桥梁静载试验主要通过测定桥跨结构在静荷载作用下控制断面的应力和挠度，从而推断出桥梁结构在荷载作用下的实际工作状态，评定桥梁结构承载能力是否达到设计荷载标准，检验成桥后结构强度、静刚度、稳定性和抗裂性等［4］。

3.1.1 测试断面及测点布置

(1)测试断面

根据《公路桥梁承载能力检测评定规程》(JTG/T J21—2011)［5］(以下简称《规程》)中有关拱桥加载测点位置的规定及参考试验现场情况，选取拱桥拱顶截面和拱脚截面作为测试断面。测试断面如图2所示。

(2)测点布置

图2 控制截面布置图

荷载试验的测点布置根据结构受力最不利位置和试验现场条件进行布置。各测试断面主要布置应变和挠度测点。测点布置如图3、图4和图5所示，其中13号测点为动应变测点。

图3 S1截面处空心板应变和挠度测试点布置图

图4 拱顶处拱肋上应变测试点布置图(单位:cm)

图5 拱脚截面拱肋上应变测试点布置图(单位:cm)

3.1.2 静载试验内容

(1)工况一:拱顶截面最大正弯矩中载工况。顺桥向按拱顶截面最大正弯矩的最不利位置布载，横桥向对称布载。

(2)工况二:拱顶截面最大正弯矩偏载工况。顺桥向按拱顶截面最大正弯矩的最不利位置布载，横桥偏载。

(3)工况三:拱脚截面最大负弯矩中载工况。顺桥向按拱脚截面最大负弯矩的最不利位置布载，横桥向对称布载。

3.1.3 试验荷载

此桥试验共需加载车4辆，加载车辆总重为35 t的三轴自卸车，轴重分配为14 t，14 t，7 t。为实现对加载试验的实时控制，保证结构安全，在试验过程中，加载车辆分级加载，及时将实测控制数据及应力、挠度等换算处理，并与计算值进行对比，以判断试验荷载下的结构性能。由《规程》的规定，本文利用内力等效原则确定静力荷载试验效率，测试的工况及荷载试验效率见表1。

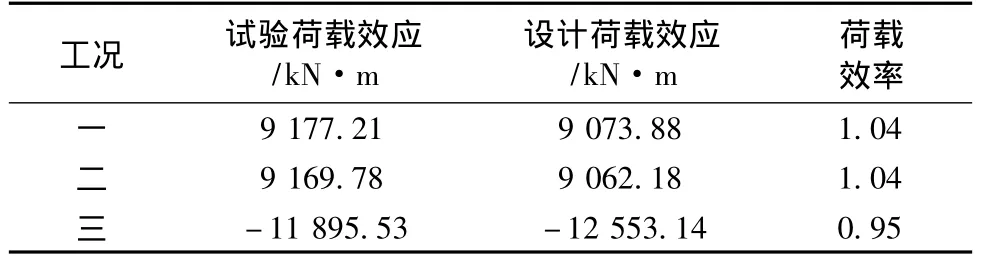
表1 加载效率表

3.2 动载试验方案

桥梁动载试验主要包括主体结构自振特性测试、行车动力响应测试。测试参数包括自振频率、振型、阻尼比和冲击系数，检验桥梁的动刚度和行车性能是否满足要求［6］。动应变测试位置选择在拱肋拱顶截面。

3.2.1 自振特性

采用频域法中峰值拾取法，也是目前桥梁模态识别的主要方法，该操作简单、识别快，利用环境激励下的响应信号识别模态参数，无需激振设备［7-9］，用高精度超低频加速度传感器做拾振器，使用DHMA模态软件分析该桥的自振特性，得到该桥的动力参数，进而对桥梁结构整体状态和工作性能进行评估。

3.2.2 无障碍行车试验

采用1辆总重约为35 t的载重汽车，在桥面上无任何障碍的情况下，受到篇幅限制，以30 km/h、40 km/h的速度驶过桥跨结构的数据，利用动态数据采集仪器配便携计算机测试测点应变在时域中的变化，根据控制截面测点在行车试验时记录的动应变曲线进行分析处理计算活载冲击系数。

3.3 静、动刚度

随着服役期的增长，桥梁结构性能会发生变化，结构动力特性也会有较大的变化，动刚度EID会受到更多更复杂的因素影响，如桥梁边界约束条件的变化，其值与梁在静力作用下的刚度EIS明显不同，贺栓海、宋一凡等对此做了大量研究［10-12］。结构的振动特性反映的是整体结构，与单梁没有明显的联系。随着荷载的增加，梁的静、动刚度也不断降低，其降低的速率不同，如矩形梁静刚度始终大于动刚度，但T梁静、动刚度减小速率与矩形梁相反，T梁静刚度有可能大于其动刚度。钢筋混凝土桥梁结构动态工作机理还未得到透彻揭示，本文为拱桥体系提供了一定的数据参考。

4 试验结果及分析

4.1 静载试验结果与分析

各测点变形(或应变)计算公式:

式中，St、Se和Sp分别为试验荷载作用下量测的结构总变形(或总应变)值、结构弹性变形(或应变)值和结构残余变形(或应变)值;Si为加载前的测值;Sl为加载达到稳定时的测值;Su为卸载后达到稳定时的测值［13］。

4.1.1 挠度分析

利用精密水准仪对桥面两边挠度测点进行测量，利用试验荷载(满载)作用下挠度在桥面两边的分布情况，得到控制截面的静刚度特性，桥面挠度校验系数见表2。

表2 工况一挠度分析结果

测试结果表明，实测最大的挠度均小于有限元计算值，挠度校验系数为0.64、0.70、0.81 和0.54，满足《规程》中小于1的要求，由此说明在试验荷载作用下S1和S2测试截面的静刚度EIS满足设计要求。桥面相对残余挠度较大与桥梁的技术状况不良，梁板存在多条裂缝相吻合。

4.1.2 应变分析

拱肋各测点的实测数据见表3。拱肋应变校验系数均满足《规程》中不大于1的要求，说明在试验荷载下，拱肋强度满足设计要求。拱肋相对残余应变均超过《规程》中20%的规定，说明拱肋在试验荷载作用下弹性状态不佳，在较大的车辆荷载下，拱肋会发生塑性变形。

表3 拱肋应变校验系数

4.2 动载试验结果与分析

4.2.1 自振特性结果与分析

(1)实测自振特性

利用DHMA模态软件计算自振特性，如图6～图8所示，自振频率、阻尼比及振型特征说明见表4。

图6 自振特性测试时程曲线

图7 自振特性测试幅值曲线

图8 竖向1阶模态试验分析结果

表4 动力分析实测结果

(2)有限元计算自振特性

由Midas Civil 2012软件计算得到本桥自振频率和振动特征。

(3)实测结果与有限元计算对比分析

由于该桥空心板、拱肋及拱座存在着较多裂缝，部分支座缺失，全桥刚度必定受到影响，竖向振动实测频率0.98明显小于计算值1.12(表5)，说明实际的动刚度小于计算刚度，结构刚度稍有削弱［14-15］，振型特征一致，由时域曲线分析结果可以看出，桥梁振动阻尼系数较大，结构耗能较快(图9)。

表5 动力分析计算结果

图9 竖向1阶振型计算结果

4.2.2 无障碍行车试验结果分析

(1)实测行车试验

大桥行车试验中动应变测试的结果如图10所示。

图10 实测动应变时程曲线

由动应变曲线计算出各工况的实测冲击系数，进行加权处理后分别为 0.05，0.11。

(2)有限元计算行车试验

通过Anil K C的对称三角形脉冲力理论，本文利用Midas Civil软件计算得到应力时程曲线，进行加权处理后得到冲击系数0.03和0.08，如图11所示。

图11 应力时程曲线

将各工况的冲击系数实测值与计算值对比，见表6。计算值和实测值较接近，由于部分墩顶负弯矩较大，导致桥面铺装存在多条横向裂缝，冲击系数的实测值比计算值稍大。

表6 冲击系数实测值及计算值分析比较

(3)行车试验校验系数结果分析

行车试验校验系数结果分析见表7。对比行车试验中测点最大实测和计算的响应值，桥梁结构具有一定的安全储备，行车试验的结果与静载试验结果也较接近，试验结果可靠。

表7 校验系数

5 结论

该桥的技术状况评定为3类桥，通过现场试验、试验数据以及试验结果的分析，可得到以下4点结论:

(1)静载试验结果表明，该桥的挠度和应变校验系数均满足规范要求，说明测试截面S1和S2的静刚度和强度均满足设计要求，但大部分残余值超过20%，根据该桥出现的裂缝和其他技术状况，在较大车辆荷载下，会发生塑性变形。

(2)自振特性分析结果表明，由于该桥空心板、拱肋、拱座和防撞护栏存在着较多裂缝，多跨部分支座丧失功能，边界条件发生较大变化，全桥刚度必定受到影响，竖向振动实测基频小于计算值，说明实际桥梁的动刚度小于计算刚度。

(3)冲击系数结果表明，由于部分墩顶负弯矩较大，导致桥面铺装存在多条横向裂缝，无障碍行车得到的冲击系数略高于计算值，结构冲击系数直接关系到桥梁的安全和经济性能，这种现象会缩短桥梁的行驶寿命，并加剧路面的破坏［16］。

(4)行车试验校验结果表明，结构在动载试验中，桥梁具有一定的安全储备。

由于该桥在外观检测中发现多跨简支空心板梁的支座脱空、剪切变形严重、支座偏位严重，拱座出现较多裂缝，边界条件发生较大变化，导致动力特性中的动刚度降低幅度比静刚度大，该桥尚能维持正常使用，但试验数据分析出的问题与该桥技术状况有关。

[1] 肖勇刚,胡丽湘.基于荷载试验的预应力空心板桥承载能力分析[J].公路与汽运,2014,30(1):210-214.

[2] 刘又佳,季云峰.浅谈荷载试验校验系数[J].城市道桥与防洪,2011,26(3):135-138,166.

[3] Anil K C.Dynamics of structures——Theory and Application Earthquke Engineering[M].Upper Saddle River,NJ:Prentule Hall,2006.

[4] 郭莹,姚勇.德阳王官村互通式立交桥连续梁静动荷载试验分析[J].四川建筑科学研究,2011,37(5):78-81.

[5] JTG/T J21-2011,公路桥梁承载能力检测评定规程[S].

[6] 王丽,孙立,霍立飞.某连续梁桥荷载试验分析[J].工业建筑,2014,51(S1):377-379,369.

[7] 续秀忠,华宏星,陈兆能.基于环境激励的模态参数辨识方法综述[J].振动与冲击,2002,21(3):3-7,91.

[8] 王俊,郑军华,陈策.运营状态下杨浦大桥模态试验与状态评估方法研究[J].公路交通科技,2009,26(7):105-108.

[9] 李闯,赵素锋.桥梁结构快速检测鉴定方法的研究[J].公路交通技术,2004,21(6):60-65,85.

[10] 贺拴海,郭琦,宋一凡,等.RC桥梁健康状况及承载能力的动力评估试验[J].长安大学学报:自然科学版,2003,23(6):36-39.

[11] 宋一凡,周彦军,贺拴海.钢筋混凝土梁的动刚度分析[J].西安公路交通大学学报,1998,18(S2):14-18.

[12] 贺拴海,徐兴.多梁式混凝土桥梁结构刚度的裂缝特征——动力分解综合识别法[J].土木工程学报,2006,39(8):91-95.

[13] 蓝宝,花尉攀,汲生伟.MIDAS在桥梁检测荷载试验仿真中的应用[J].低温建筑技术,2009,31(5):55-57.

[14] 黄力,石雪飞,徐亮.大跨度连续梁桥动静载试验及结构评定[J].石家庄铁道大学学报:自然科学版,2012,25(3):24-29.

[15] 吴桂林,赵宾.小跨径板梁桥承载力快速评定模型研究[J].公路,2014,59(6):321-324.

[16] 黄立葵,盛灿花.车辆动荷系数与路面平整度的关系[J].公路交通科技,2006,23(3):27-30.