双分数跳-扩散环境下的可转换债券定价

金宇寰， 薛红， 冯进钤

(西安工程大学理学院， 西安710048)



双分数跳-扩散环境下的可转换债券定价

金宇寰， 薛红， 冯进钤

(西安工程大学理学院， 西安710048)

可转换债券是一种兼具债券和期权特性的混合型高级金融衍生产品，其合理定价对发行人和投资者都具有重要的现实意义。在考虑企业市场价值波动和利率波动的基础上，假定股票价格遵循双分数Brown运动及跳过程驱动的随机微分方程，利率满足Vasicek模型，建立了双分数跳-扩散环境下的金融市场数学模型，利用双分数布朗运动的随机分析理论和保险精算方法，讨论了可转换债券定价问题，得到了双分数跳-扩散环境下的可转换债券定价公式，在现有研究的基础上对可转换债券定价公式进行了进一步的研究和推广，使模型更加贴近实际金融市场。

双分数跳-扩散过程；可转换债券；保险精算；随机利率

引言

可转换债券是一种企业债券和股票期权相结合的混合证券，对其合理定价非常重要。近年来，随着金融工程、数值算法和信息技术的发展，可转换债券的定价逐渐成为国内外的热点研究课题，一系列研究模型与方法相续出现。但目前比较常用的研究方法是基于偏微分方程或鞅方法的定价研究。文献[1]利用分数布朗运动随机分析理论与方法，得到可转换债券的定价公式；文献[2]假定股票价格服从带跳的分数布朗运动，利率满足Vasicek模型，得到可转换债券的定价公式。双分数布朗运动是一种比分数布朗运动更为广泛的高斯过程，它不仅具有自相似性和长期记忆性等分数布朗运动具有的性质，而且在一定限制条件下是一个半鞅。为了刻画金融资产的长期记忆性以及消除分数布朗运动市场中的金融套利，本文用双分数布朗运动刻画金融资产的价格变化，关于双分数布朗运动的概念和性质可以参见文献[3-6]。MogenBladt与Tina Hvid Rydberg于1998年首先提出期权定价的保险精算方法，该方法在一定程度上克服了基于无风险套利、复制思想得到的Black-Scholes模型假设严格、公式推导较为繁琐的缺点，关于保险精算的概念及其在期权定价中的应用可参见文献[7-9]。本文假定股票价格方程服从双分数Brown运动及跳过程驱动的随机微分方程，利率满足Vasicek模型，建立金融市场数学模型，结合保险精算方法，得到可转换债券定价公式。

1 双分数跳-扩散环境下金融市场模型

其中，H∈(0,1),K∈(0,2)。

当K=1时，双分数布朗运动就退化为分数布朗运动，当K=1,H=1/2时，双分数布朗运动就退化为标准布朗运动。

假定股票价格S(t)和利率r(t)分别满足随机微分方程

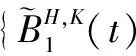
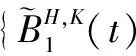
(1)

(2)

引理1随机微分方程(1)的解为：

则

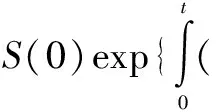
若在T1∈[0,t]时刻发生一次跳跃，则

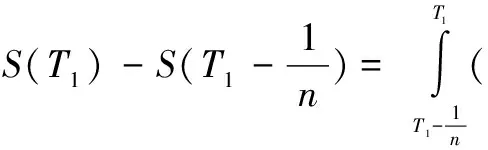
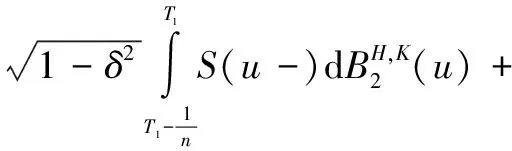
当n→∞时，S(T1)-S(T1-)=

S(T1-)U1，所以

若跳跃次数服从泊松过程，则引理1结论成立。

引理2随机微分方程(2)的解为

则

从而可证结果。

引理3[2]假定a,b,c,d,k为实数，其中ξ1～N(0,1),ξ2～N(0,1)，cov(ξ1,ξ2)=ρ，则有

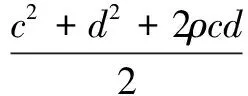
其中，Φ(x)为标准正态分布函数。

引理4[10]假定a,b,c,k为实数，其中ξ1～N(0,1),ξ2～N(0,1),ξ3～N(0,1),cov(ξ1,ξ2)=0,cov(ξ2,ξ3)=0,cov(ξ1,ξ3)=ρ,则有

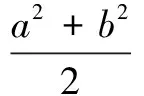
其中，Φ(x)为标准正态分布函数。

定义2[11]股票价格{S(t),t≥0}在[0,t]上的期望回报率β(u),u∈[0,t]定义为

引理5股票价格{S(t),t≥0}在[0,t]上的期望回报率β(u),u∈[0,t]为β(u)=μ(u),u∈[0,t]。

证明由引理1可知

又因为

从而可得结果。

2 可转换债券定价公式

定义3[2]假设可转换债券只在债券到期时刻T发生转换，则可转换债券到期时的现金流量VT可以表示为

其中，VT表示可转换债券到期时刻T的价值，Pb表示纯债券价值，C表示转换价格，M表示债券面值，S(T)表示T时刻股票价格。

定义4[2]具有红利支付的可转换债券在0时刻的保险精算价格定义为

定理1可转换债券的保险精算价格为

其中，Φ(x)为标准正态分布函数，且

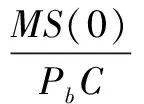
D1=σ2δ2T2HK

D2=σ2(1-δ2)T2HK

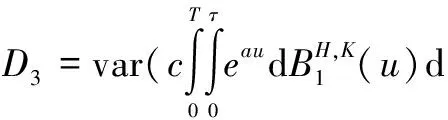
证明令

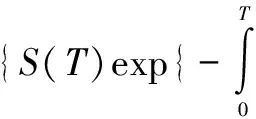
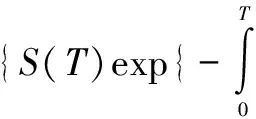
由引理1可得

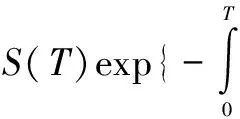
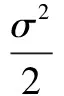
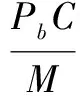
因为

则

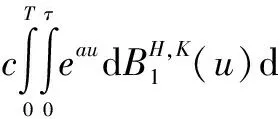
其中，

ξ1～N(0,1),ξ2～N(0,1),ξ3～N(0,1)

且

cov(ξ1,ξ2)=0,cov(ξ2,ξ3)=0,cov(ξ1,ξ3)=ε

记

则有

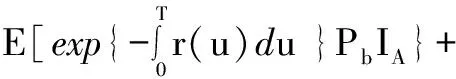
其中

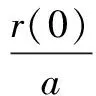
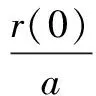
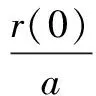
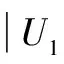
令

则

由引理3

所以

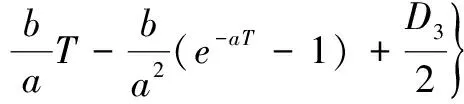
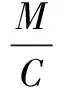
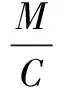
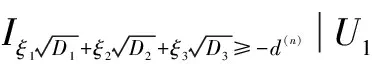
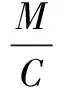
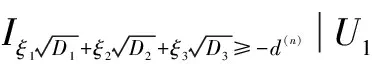
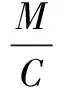
注1当K=1时，可得分数跳-扩散环境下支付红利的的可转换债券的保险精算价格[2]。

其中，Φ(x)为标准正态分布函数，且

D1=σ2δ2T2H

D2=σ2(1-δ2)T2H

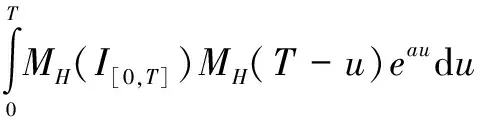
MH的定义见文献[12]。

特别地，当K=1,b=0,c=0,a→0时，可得文献[1]结果。

[1] 李军,薛红,李艳伟.分数跳-扩散过程下可转换债券定价[J].佳木斯大学学报:自然科学版,2010,28(3):440-448.

[2] Xue Hong,Li Chenwei.An Actuarial Approach to Convertible Bond Pricing in Fractional Jump-diffusion Environment[J].Computer Science and Service System,2012,8:79-82.

[3] Es-sebaiy K,Tudor C A.Multidimensional Bifractional Brownian motion: Ito and Tanaka formulas[J].Stochasties and Dynarmes,2007,7(3):365-388.

[4] Russo F,Tudor C.On the bifractional Brownian motion[J].Stochastic Processes and their Applications,2006,116(5):830-856.

[5] 徐锐,申广君,祝东进.一类双分数布朗运动迭代过程局部时的存在性和联合连续性[J].应用数学,2014,27(3):637-646.

[6] Mather G,Murdoch L.Evidence for global motion interactions between first-order and second-order stimuli[J].Perception,1999,27(7):761-767.

[7] 郑红,郭亚军,李勇,等.保险精算方法在期权定价模型中的应用[J].东北大学学报:自然科学版,2008,29(3):429-432.

[8] 文金明,刘锡标.保险精算学原理在可转债定价模型中的运用[J].时代金融,2008(11):41-44.

[9] 柯政,秦梦.同质信念与Black-Scholes公式定价偏差——基于期权定价的保险精算方法[J].经济数学,2015,32(2):15-20.

[10] 陈松男,金融工程学[M].上海:复旦大学出版社,2002.

[11] Xue Hong,Lu Junxiang,Li Qiaoyan,et al.Fractional jump-diffusion pricing modelunder stochastic interest rate[J].Information and Financial Engineering,2011,12,428-432.

[12] Biagini F,Hu Y,Oksendal B,et al.Stochastic calculus for fractional Brownian motion and applications[M].New York:Springer,2008.

2015年总目录

(篇名/作者/期数/页码)

化学、生物及材料科学

苯二甲酸插层水滑石的制备和结构表征

王 军，蒋 燕，刘水红，杨 敏，余达艺，路 璐1(1)

电流密度对AZ31镁合金阳极氧化膜的影响

熊中平，司玉军，李敏娇1(5)

钼系复合缓蚀剂性能研究

向云刚，崔益顺，谯康全1(9)

离子液体制备碳氮硫共掺杂TiO2及其光催化性能的研究

陈久福，钟俊波，李建章，程朝柱，窦 琳1(12)

几种无机离子和氨基酸对酿酒酵母酒精耐性的影响

梁泽新，王 川，戴 川2(1)

浓香型大曲中多株芽孢杆菌的分离及鉴定

王 勇，罗惠波，刘燕梅，王艳丽，叶光斌2(5)

表面增强拉曼光谱检测白酒中氨基甲酸甲酯含量研究

徐晨曦，付大友，谭文渊，汪 菊2(9)

3.5 %NaCl薄液膜下碳钢的腐蚀行为研究

杨 丽，林修洲，梅拥军，李 月，崔学军，罗淑文3(1)

配制型桑椹醋生产工艺研究

王艳丽，邓 杰，卫春会， 钟姝霞，祝云飞，黄治国4(1)

变压吸附法脱除甲醇裂解气中CO_CO2研究

刘吉顺，何 芬，李可彬4(5)

丢糟综合优化利用研究

张德荣，张蜀艳,唐自慧5(1)

纯种根霉麸曲制曲工艺优化研究

罗惠波，谢 军，黄治国，边名鸿，王大地， 杨文斌5(7)

2-氟异烟酸和1,10-邻菲罗啉的稀土配位聚合物的合成、结构及荧光性质

吴威平，吴 宇，路 璐，孙延春5(12)

仙茅酒对小鼠抗疲劳作用的影响

潘 明,陈欲云,刘春丽,邬亚平, 代联伶,陈利娟6(1)

硫酸溶液中[双(4-甲氧基苯基)]二硫代磷酸二乙铵对碳钢的缓蚀性能研究

赖 川6(5)

对羟基苯基乙酸锌配位聚合物的合成、晶体结构及荧光性质

路 璐，阿洛伍各，王凤莲，余小芳，钟艳蓉，景 倩6(11)

酒曲中产酯酵母的分离筛选

万世旅，李光辉，钟姝霞，边名鸿6(16)

机械、电子及计算机科学

利用HTML5拖放技术实现多文件异步上传

刘耀钦1(17)

基于PLC的立体车库自动控制算法的设计及应用

霍 沛,胡 勇1(21)

基于自适应模糊PID方法的轮毂无刷直流电机控制与仿真

刘秋生,吕 欣，谭妍玮,张众华,陈 启1(25)

两种抗时间片的攻击方法

姜海芳,王海沛,杨 威2(14)

往复活塞式空压机连杆有限元分析与结构优化研究

刘晓叙,肖 迪,蒲 虎2(18)

预制螺旋槽薄壁管的吸能研究

李玉如,柳忠彬,肖守讷,王 欢2(21)

基于Rayleigh法的简支梁桥自振频率计算

朱谊彪,李扬2(26)

基于多种群遗传算法的装配线平衡问题研究

李 锋,邢静忠，刘 伟2(30)

微电机盖板多工位级进模设计

王春香2(37)

脉冲电源三维电极法处理钻井废水的实验研究

庞 凯，梁 宏，肖惠文，吴思斯，刘 嘉2(40)

基于并行计算的高效图稀疏化处理算法

李 融2(45)

混合智能在递归神经网络软测量中的应用

王 杰,古奋飞2(52)

电动式EGR阀流固耦合共轭传热研究

付 磊,李 良,罗云蓉,唐克伦,李泽平,赵贻富3(5)

基于ANSYS/LS-DYNA分析平头弹侵彻间隙式双层靶的失效模式

刘 兵,王红红,邓勇军3(11)

回归正交试验在冷冲拉深成形中的应用研究

陈 刚,胡 勇3(16)

Android平台的移动APP开发方法与应用研究

韩文智,骆文亮3(22)

支持增量图数据的超图查询算法研究

孙勤红3(27)

一种用于超分辨率重建的自适应块匹配算法

唐 玲,陈明举3(33)

面向智能家居中生理参数监测的安防系统网关设计

于明涛，陈 超，叶晓彤3(37)

基于暗原色先验的低照度图像增强

黄 勇,孙兴波,袁文林,范云飞3(42)

MO_DE：一种结合多目标优化机制的DNA编码序列算法

岑 巍3(46)

工业过程噪声干扰下图像关心区域分割算法研究

张宗璐3(51)

基于AD9833的智能信号发生器设计与仿真

高 祥,杨小锐,蔡乐才,居锦武,高媛媛3(57)

风力机尾流场及相互作用的实验研究

杨 瑞,王小丽,王 强,张志勇4(11)

基于Fluent的考虑旋转车轮影响的汽车外流场分析

谭妍玮,张众华,刘秋生4(17)

测量不确定度的BP神经网络模型

房亚群,吴一凡4(22)

基于智能集成粒子群算法的时间序列数据挖掘研究

张 健4(27)

嵌入式Linux内存管理的优化

于国龙,崔忠伟,左 羽4(33)

基于NCC匹配的Camshift目标跟踪算法

郑朝晖4(37)

基于RBF神经网络的Duffing混沌系统控制

周群利4(41)

基于Hash函数的轻量级RFID双向认证协议

龚海余,李 飞,赵国娟4(45)

基于HTM算法的恶意Android应用检测

仇慎健，张仕斌，刘苹光4(50)

Dynamic Numerical Simulation of a High Speed Train Passing Through Tunnel

XU Wei, YANG Yiren , WEN Huabin5(16)

屈曲约束支撑力学模型对比分析

周小林，雷劲松5(21)

格值一阶逻辑系统LF(X)中的α-有序语义归结

张家锋，曹发生5(27)

基于Logistic混沌-贝努力序列的循环压缩测量矩阵构造算法

臧华中5(31)

无线传感器网络中基于粒子滤波的目标跟踪算法研究

郑爱媛5(37)

基于滑膜控制和SAFNN的鲁棒混沌同步

边潇俊，林 达，谢玉姣5(44)

基于模式识别的Lebesgue积分在PVS中的形式化证明与分析

张少芳，李冀东5(51)

基于在线视频学习的用户观看行为抽取方法

王 东，林 宏，左 欣6(20)

30 kW异步起动永磁同步电机的优化设计

王 亮,王 晨,黄金霖6(25)

改进的LS-SVM数学模型的交通流量预测分析

吴一凡6(29)

基于FOA优化BP神经网络的电子商务网站评价研究

秦艳华6(36)

基于电磁导航智能车的控制研究及实现

吴 祥,王冠凌6(42)

无线传感器网络IRBS时间同步优化算法

凌海波,陈 妤，周先存6(47)

基于改进小波神经网络的短时交通流量预测研究

曹 莉,唐 玲,吴 浩,高 祥,乐英高6(52)

帧间差分法在视频监控中的应用研究

李 亮,罗 毅6(58)

RF MEMS并联开关的结构设计及分析

许马会,刘凤丽,郝永平6(63)

基于EPON接入的园区网视频监控设计

毛乾任，王朝斌6(68)

工程质量、安全与防灾减灾

各国规范中对预应力混凝土结构损失的计算方法分析比较

黄 颖，高 杰1(31)

T梁C55高性能混凝土配合比设计研究

景淑媛，杜文举，杨元意1(36)

Analysis of Damages Caused by Earthquakes to Traffic Facilities in Mountainous of West China

WANG Wenqi，LIU Baoxian, LI Li, ZHOU Xiaowen, WANG Ze1(41)

预应力孔道灌浆密实度检测评价技术体系的研究

张武毅1(46)

基于EMD技术的弹性波信号降噪技术

王闺臣，李 科，吴佳晔1(50)

许卡滑坡的影响因素及其稳定性分析

古彦超，崔亚昆1(54)

深基坑上部土钉墙土钉轴力监测及分析

刘安宁，来庆专，吴瑞刚，苏长毅1(59)

深基坑桩锚支护下桩后土体深部水平位移的研究分析

来庆专，吴瑞刚，陈 磊，刘安宁，荆周宝2(57)

汶川地震与芦山地震次生地质灾害特征对比

王怡璇，朱利东，杨文光，李 超，李敬波，陈 顺2(63)

盾构隧道近距离侧穿桩基的施工力学响应研究

高俊涛，黄雪阳2(69)

海洋生物膜对混凝土耐久性影响

刘虎城，李 猛，徐学斌，邬晓光2(74)

地震多发地区道路防水损害路面维养材料研究

谢远新，王 泽，罗忠贤，王文奇，王宠惠2(78)

在建高速公路路堑边坡垮塌成因分析及处治措施

席称心，陈 磊2(81)

超载作用下中美规范响应分析

闵亚芝，孙华强，赵 吉2(86)

大跨度结合梁斜拉桥非线性动力特性研究

王 伟3(66)

锚杆长度无损检测的影响因素分析

訾建峰，杨 森3(71)

自锚式悬索桥主缆架设监控

包大海，袁堂超，陆久飞3(76)

L型和矩形低矮房屋体型系数对比研究

姚 望，姚 勇，李 明4(57)

预应力碳纤维布加固效果试验研究

李永东4(62)

超声波及表面波法在检测含水裂缝深度中的应用分析

张小龙，赵 鹏，徐浩铭，徐 港4(66)

矮塔斜拉桥的动力特性分析

朱 强，刘 菲4(72)

地震作用下中小跨径空腹式拱桥腹拱病害评价方法改进

陶庆东，肖伦斌5(57)

水泥混凝土路面的温度梯度研究

曾惠珍5(62)

基于冲击弹性波CT的桥墩缺陷无损检测

张育斌5(69)

碳纤维布加固钢管轴压短柱有限元分析

李兆阳，高小育，陈沿辰5(74)

预应力孔道压浆密实度检测技术在连续刚构桥中的应用

宋景景6(73)

某特大跨径拱桥静动载试验分析与评价

耿 泽，孙亚民，裴存栋6(77)

某滑坡稳定性的FLAC-3D数值模拟研究

张艳阳，任光明6(83)

数理基础科学

曲面上测地线和短程线的性质

邢家省，高建全，罗秀华1(63)

一类具粘性阻尼项的拟线性波动方程解的存在性

宋瑞丽，王宏伟1(67)

基于偏最小二乘法的PM2.5相关因素分析研究

卢 鹏，何 杰，彭丛笑1(71)

椭圆型最优控制问题中的L1,2-方向稀疏

严春梅，张 维1(76)

两个相依部件并联系统和有冷贮备部件串联系统的模糊可靠性

汪军芳，张民悦1(80)

VaR准确性检验的T检验法

唐 宁，冯长焕1(83)

基于风险偏好的PPP项目风险分担的三方博弈模型

葛 果，侯 懿1(87)

集合约束下的向量拟均衡问题

代乾文1(92)

几乎基次亚紧空间的无限乘积

石鹏飞，何兆容，张焰杰1(98)

动态区间值模糊软集及其决策应用

何 霞，杜迎雪，刘卫锋2(92)

变分法的灵敏度分析及其在分布式水文模型的应用

王雪娇，钱伟婷，杜 鹃，翁云华2(97)

高斯曲率绝妙定理的几种公式的推导方法

邢家省，高建全，罗秀华3(80)

Hilbert空间中解凸集约束优化问题的梯度投影算法

杨 丽3(86)

Robin型无穷多点边值问题正解的存在性

覃仕霞，罗 圆3(90)

广义均值不等式及其简单应用

王 琳，杨 秀3(96)

曲面正交网下测地曲率计算公式的推导方法

邢家省，白 璐，高建全4(75)

Hilbert空间中一类新广义非线性变分不等式组问题

罗 静，隆建军4(80)

广义拓扑的比较

宋颖潇，丁 猛，朱培勇4(86)

无约束优化算法比较及其极值点研究

毛 巍，兰恒友4(89)

基于DEA的经济绩效视角分析新疆工业企业民营化改革

张 淼4(95)

曲面上三个基本形式关系的证明方法

邢家省，白 璐，罗秀华5(81)

基于灰色关联与投影算法的铁路货运量影响因素分析

梅晓玲5(85)

向量值集值形式广义博弈Nash平衡的存在性

计 伟，张珺铭5(89)

S-σ-仿Lindelof空间和S-σ-仿紧空间及其乘积性质

丁 猛，朱培勇5(93)

带非线性记忆边界条件的热方程组解的爆破问题

李慧芳5(97)

开关寿命连续型三不同型部件温贮备可修系统可靠性分析

张民悦，姜明明6(87)

双分数跳-扩散环境下的可转换债券定价

金宇寰，薛 红，冯进钤6(92)

2015年1～6期总目

6(97)

Convertible Bonds Pricing in Bifractional Jump-diffusion Environment

JINYuhuan,XUEHong,FENGJinqian

(School of Science, Xi’an Polytechnic University, Xi’an 710048, China)

Convertible bond is a hybrid advanced financial derivatives with both features of bonds and options, and the reasonable pricing have important practical significance to issuers and investors. In this paper, on the basis of considering the volatility of enterprise market value and interest rates, assuming that stock price follows stochastic differential equations of bifractional Brownian motion and jumping process-driven, and the interest rate satisfies Vasicek model, the mathematical model of the financial market in the bifractional jump-diffusion environment is built. Using the stochastic analysis theory of bifractional Brownian motion and actuarial methods, the pricing problem of convertible bond is discussed, and the convertible bond pricing formula in bifractional jump-diffusion environment is obtained. On the basis of existing research the further research and promotion on convertible bonds pricing formula is done, so as to make the model more close to the actual financial markets.

bifractional jump-diffusion process; convertible bond; actuarial science; stochastic interest rate

2015-09-07

陕西省教育厅自然科学专项基金(12JK0862)；陕西省自然科学基础研究计划资助项目(2015JM1034)

金宇寰(1991-)，女，陕西安康人，硕士生，主要从事金融数学方面的研究，(E-mail)215845655@qq.com； 薛 红(1964-)，男，山西万荣人，教授，主要从事随机分析与金融工程、保险精算等方面的研究，(E-mail)xuehonghong@sohu.com

1673-1549(2015)06-0092-05

10.11863/j.suse.2015.06.19

F830；O211

A