基于回归分析的研究及R语言实现

杨姗姗，王松会，宋东东

(华北水利水电大学 信息工程学院，河南 郑州450011)

近年来，随着煤炭销售量的持续走低，如何提高煤炭的销售量已成为天安运销公司的首要难题，除却煤炭市场的影响，发热量测定时间与煤炭装车时间的矛盾也是影响煤炭销售的不可忽略的因素，在以往的研究中，已得到煤炭的灰分与发热量之间存在着负相关，即煤炭的灰分越大，发热量越小，从而可从煤的灰分得出其发热量。然而，灰分的测定依然耗时，无法实现煤炭发热量的快速估算，在此基础上，本文提出了用煤的密度快速估算发热量的方法，用线性拟合的数学方法得出煤的密度与发热量的函数关系，从而实现了煤炭发热量的快速估计，间接提高煤炭的销售量。

1 回归分析

1.1 曲线拟合

通常实验和勘测常会产生大量的数据。为了解释或根据这些数据作出预测、判断，给决策者提供依据，需要对测量数据进行拟合，寻找一个反映数据变化规律的函数。数据拟合方法与数据插值方法不同，其所处理的数据量大且不能保证每一个数据没有误差，所以要求一个函数严格通过每一个数据点并不合理。数据拟合方法求拟合函数，插值方法求插值函数。这两类函数最大的不同之处是，对拟合函数不要求它通过所给的数据点，而插值函数则必须通过每一个数据点。

1.2 线性拟合

假设拟合函数是线性函数，即拟合函数的图形是一条平面上的直线。而表中的数据点未能精确地落在一条直线上的原因是实验数据的误差。

下一步确定函数中系数a和b。从几何背景来考虑，就是要以a和b作为待定系数，确定一条平面直线使得表中数据所对应的10个点尽可能地靠近这条直线。一般来讲，数据点将不会全部落在这条直线上，若第k个点的数据恰好落在这条直线上，则这个点的坐标满足直线的方程，若这个点不在直线上，则其的坐标不满足直线方程，有一个绝对值为的差异(残差)，于是全部点处的总误差是

这是关于a和b的一个二元函数，合理的做法是选取a和b，使得这个函数取极小值。但在实际求解问题时为了操作上的方便，通常是求a和b使得函数

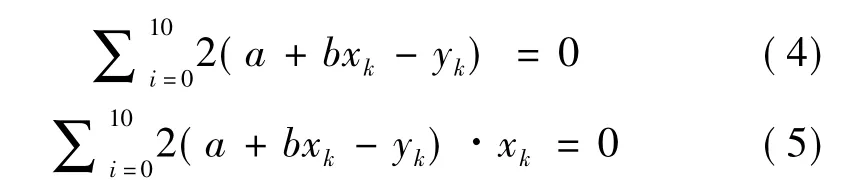
这是关于未知数a和b的线性方程组，其被称为法方程。

2 R语言

R语言的语法表面上类似于C语言，但在语义上是函数设计语言的变种且与Lisp及APL有较强的兼容性。R语言的主要思想是可以提供一些集成的统计工具，同时其允许在“语言上计算”，提供了各种用于数学计算、统计计算的函数，使得用户可将表达式作为函数的输入参数或只需指定数据库和若干参数便可进行灵活方便的数据统计和分析，该做法有利于统计模拟和绘图，甚至允许用户创造出符合其需要的新的统计计算方法［1－2］。其功能主要包括:进行数据存储和处理;进行数组运算，尤其在向量、矩阵运算方面的功能强大;进行完整连贯的统计分析和制图;作为编程语言简便而强大地操纵数据的输入并实现分支、循环，同时支持用户自定义功能。

3 平煤密度与发热量的分析

本文通过一组在平顶山运销公司测定的一矿的密度与发热量的数据运用R工具进行分析得出其密度与发热量之间的关系，如表1所示。

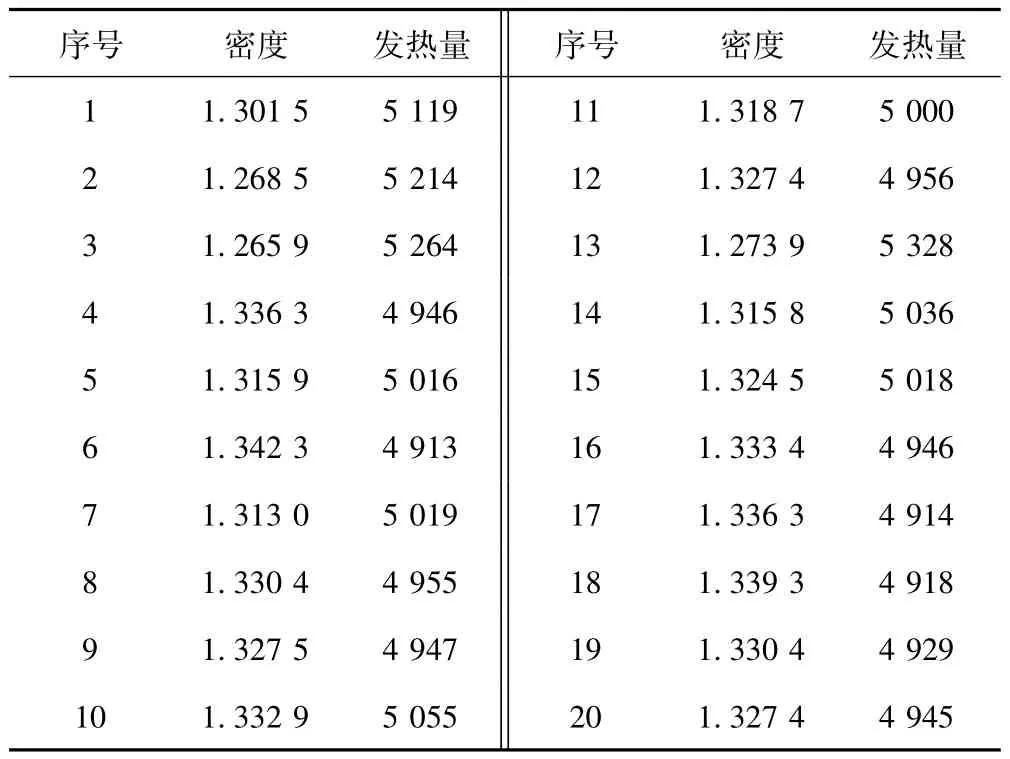
表1 密度与发热量原始测定数据

步骤1绘制散点图。散点图通常用来刻画两个连续型变量之间的关系。绘制散点图时，数据集中的每一个观测值都由散点图中的一个点来表示［3］。

步骤2数据拟合。运行stat_smooth()函数并设定method=lm即可向散点图中添加线性回归拟合线，这将调用lm()函数对数据拟合线性模型。首先，将基本绘图对象存储在对象sp中，然后，再添加更多的图形部件;默认情况下，stat_smooth()函数会为回归拟合线添加95%的置信域，置信域对应的置信水平可通过设置level参数来调整。设定参数se=false时，系统将不会对回归拟合线添加置信域［4－5］。

步骤3向散点图添加模型系数。本文采用自动提取模型对象的值并创建一个引用这些值的公式来进行数据分析，首先，创建一个字符串，对其进行解析后，会返回一个合法的公式;有了字符串表达式后，便可将其添加到图形上。

4 数据分析

在文中，70%的数据用于做数据分析，30%的数据用以做数据校验，在采用上述方法对数据进行分析整理后［6－7］，得出结果如下。

由图1可知，洗煤发热量与密度之间呈线性关系，随着密度的增加，发热量减少，在此，记发热量为y，密度为x，分析结果为y=15 022.5x+11 632，相关系数r=0.998。

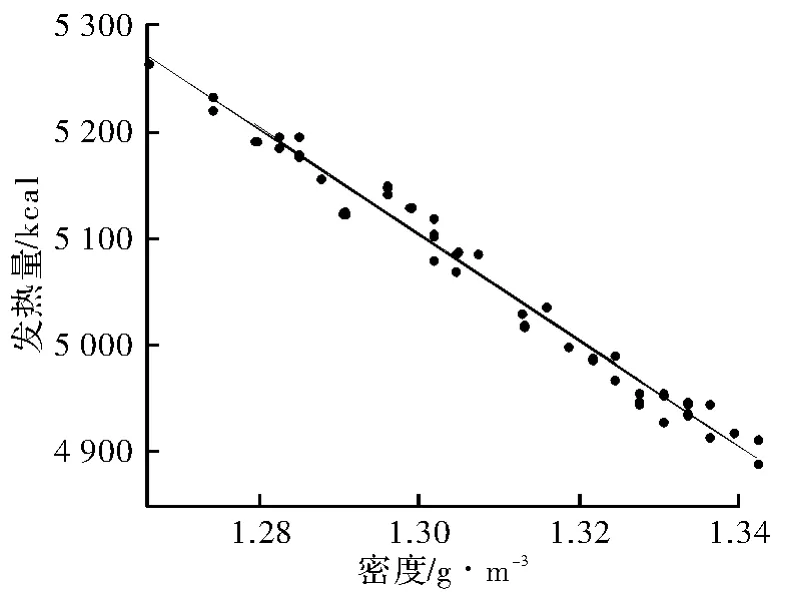
图1 洗煤密度与发热量关系图

图2中，实心点代表原始数据，空心点代表预测数据，当密度较小时，预测数据与原始数据基本贴近，而当密度值增大时，拟合效果并不理想。

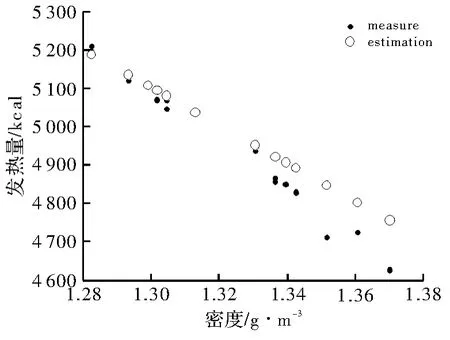
图2 洗煤预测数据与原始数据对比图

由图3可知，混煤发热量与密度之间呈线性关系，随着密度的增加，发热量逐渐减少。在此，记发热量为y，密度为x，分析结果为y=14 472x+10 514，相关系数r=0.935 7。

图3 混煤密度与发热量关系图

图4中，实心点代表原始数据，空心点代表预测数据，由图可知，预测数据与原始数据基本贴近，从而确保了回归曲线的可靠性［8－10］。

图4 混煤预测数据与原始数据对比图

5 结束语

本文通过线性回归的数学拟合方法和R数据分析工具对平顶山天安运销公司一矿的洗煤和混煤的密度和发热量进行了分析，得出了一矿煤质的密度和发热量之间的函数关系，由于煤质的密度测量方法简单快捷，可在室外直接测量得出，从而可快速的实现发热量的快速估算，间接提高煤炭的销售量，本文还进行了数据加工，剔除了数据中存在的异常点，并在线性回归的基础上进行了线性度以及残差的分析，从而确保了函数关系的可靠性。然而，本文仅针对平顶山天安运销公司的一矿的煤质进行了分析，得出的函数关系也仅对一矿的煤质成立，至于其它矿井是否也存在这样的函数关系，还需做进一步分析。

［1］ 王斌会，方匡南，谢佳斌.R语言统计分析软件教程［M］.北京:中国教育文化出版社，2007.

［2］Winston Chang.R数据可视化手册［M］.肖楠，邓一硕，魏太云，译.北京:人民邮电出版社，2014.

［3］Paul Teetor.R语言经典实例［M］.李洪成，朱文佳，沈毅诚，译.北京:机械工业出版社，2013.

［4］Venables W N，Ripley B D.Modern applied statistics with s［M］.Fourth Edition.New York:Springer－Verlag，1996.

［5］ 王实，高文，李锦涛.Web数据挖掘［J］.计算机科学，2000，27(4):28－31，41.

［6］ 吴喜飞.煤炭产品销售中的服务营销［J］.现代商业，2011(35):98－99.

［7］ 毕军贤.基于聚类的交易者煤炭质量检验可信度研究［J］.数理统计与管理，2010，29(2):219－220.

［8］ 范中启.对中国煤炭产业竞争力的探究［J］.煤炭经济研究，2005(2):38－40.

［9］ 吴峰.浅谈煤炭销售调度管理创新［J］.中国城市经济，2011(6):92－93.

［10］汪敏水.优化煤炭销售工作的策略探讨［J］.中国城市经济，2011(22):45－47.