图像代数重建算法的并行性研究
2015-04-25粟子芩徐伯庆苏栋骐
粟子芩,徐伯庆,苏栋骐
(上海理工大学 光电信息与计算机工程学院,上海200093)
计算机断层成像(CT)技术[1]是通过对物体进行不同角度的射线投影扫描而获取物体截面信息的成像技术。常用的图像重建方法主要分为:解析法和迭代法两类[2]。其中解析法只适用于投影数据完备的图像重建,但实际中往往难以检测到完备的投影数据。而代数重建(ART)算法在投影数据不完全或含噪声较大的情况下可重建出质量较好的图像。
ART重建算法计算量大,重建速度慢,因此如何加快重建速度以及如何用最少的迭代次数重建出最佳的图像成为ART算法图像重建的主要问题。近年来国内外众多学者致力于发展这种算法,如Siddon[3]能有效地计算出投影系数及对应的网格编码;Y.Censor[4]采取斜投影方式来进行代数重建;G.T.Hermany[5]将整体变分法应用于ART算法;秦中元等[6]提出内存优化的ART算法;赵双任等[7]将滤波反投影算法与代数重建算法进行结合使用并对图像分块重建等。对ART算法的不断研究,使算法的复杂度越来越高,导致重建速度也随之大幅降低。本文针对ART算法进行了并行化加速研究,提出了一种利用计算机集群将投影角度均匀分配给多个CPU同时独立运行并加权平均的方法,以实现图像的快速重建,并提高了图像质量。
1 ART算法原理
首先,将欲重建的连续图像f(x,y)离散化[8]。即将一个N=n×n的正方形网格叠加在图像f(x,y)上,在每个像素内f(x,y)是常量。fj(1≤j≤N)代表网格内第j个像素的常数值,N=n×n为像素总数,第i条射线L穿过物体的投影值pi是f(x,y)沿射线路径的线积分值。经过一次扫描,可建立重建图像和投影数据之间关系的代数方程组,因此图像重建转化成求解下列线性方程组

式(1)中,wij为投影系数,反映了第个像素对第条射线投影值的贡献,在数值上等于第条射线与第个像素重叠的面积与像素面积之比。M为投影数,取决于投影角个数和每个投影角下的射线数。将式(1)写成矩阵形式为WF=P,其中,P为M维投影数据向量;F为N维图像向量;W为M×N维投影矩阵。
通常M和N均较大,难以用常规解线性方程组的方法求解。因此,采用迭代方法[9]求解这个线性方程组。先给定一个初始值F(0),再按下列公式逐次迭代

式(2)中,i=0,1,2,…,M,λ为松弛因子,取值为0~2,k为迭代序号。在N维空间中,方程组(1)中的每个方程代表一个超平面,而图像向量F则为N维空间中的一个点。当式(1)存在唯一解时,其解必为这M个超平面的交点。迭代过程从向量初始值F(0)开始,不断对图像进行校正,当投影进行完最后一个方程所表示的超平面而得到F(M)时,为一次完整迭代。在第二次迭代中,将F(M)作为初始值重复计算式(2),得到F(2M),如此反复,直到方程收敛,即方程组(1)存在唯一解F。
2 ART并行化加速分析
2.1 计算机集群
集群(Cluster)技术[10]是指一组相互独立的计算机,利用高速通信网络或局域网组成一个计算机系统,每个集群节点即集群中的每台计算机均是运行其自身进程的一个独立服务器,这些进程可彼此通信、统一调度、协调处理以实现高效并行计算。集群计算机具有强大的处理能力、高可用性及可伸缩性,通常用于改进单个计算机的计算速度和可靠性。
2.2 ART并行化加速
实际重建中每条射线的投影值要逐条进行计算,由于在一个CPU上只运行一个进程,因此图像重建过程数据处理量大、重建速度慢。现假设投影角度数为,将个投影角度分为M部分,每部分的投影角度个数为Q=N/M(Q>0,Q为整数)。M部分中第一部分投影角度的起始角度为0°,其第Q个投影角度为(NM)°,后一部分投影角度的起始角度在前一部分投影角度的起始角度上加1°,其第Q个投影角度同样在前一部分投影角度的第Q个投影角度上加1°,如此类推,直到第M部分投影角度的起始角度为M-1°,其第Q个投影角度为N-1°;对于每部分内的投影角度来说,后一个投影角度在前一个投影角度上加M°。如此类推,直到N个投影角度分配完毕。
投影角度分配好后,将M部分投影角度分别分配给个CPU,并把其中一个CPU设定为主进程,其余M-1个CPU设定为从进程,M个CPU同时对所接收到的部分投影数据进行图像重建,各个进程完成自身所承担的任务后将运算结果返回给主进程,从而对图像向量进行更新。主进程将M-1个从进程的运算结果接收完毕并结合自身进程的运算结果,统一对其进行处理。本文采用加权平均的方法,即将M个图像向量加权平均,得到最终的重建图像。
下面举例说明,N=180,M=6,即对欲重建图像进行0°~179°投影,并将N个投影角度分为A,B,C,D,E,F共6部分,这6部分投影角度同时对图像分别进行重建,每部分的投影角度个数为Q=180/6,并且每部分内的投影角之间互隔6°,如下

最后将6个图像向量加权平均输出图像。
3 实验结果及分析
在由3个双CPU节点组成的集群系统上实验,节点的CPU采用Intel® CoreTMi5处理器。为了研究不同的集群节点个数对重建速度和质量的影响,选用经典的Shepp-Logan头模型作为重建对象。该模型由10个位置、大小和方向各异的椭圆组成。相关参数为:Shepp-Logan头模型的大小为128×128,投影角选取180个角度,松弛因子固定为1,迭代次数为1。表1是Shepp-Logan头模型采用节点数量不同的集群系统的重建时间。

表1 Shepp-Logan头模型CPU个数重建图像并行算时间表
做出CPU个数与加速倍数之间关系的曲线,如图1所示。

图1 Shepp-Logan头模型CPU个数相对于单个CPU的加速倍数曲线
并行运算结果表明:图像重建速度与CPU个数基本上成线性正比关系,在本例中相对于单个CPU可提高近12倍。
图2所示为Shepp-Logan头模型分别分成1、2、3、4、5、6部分进行并行重建的结果图像。
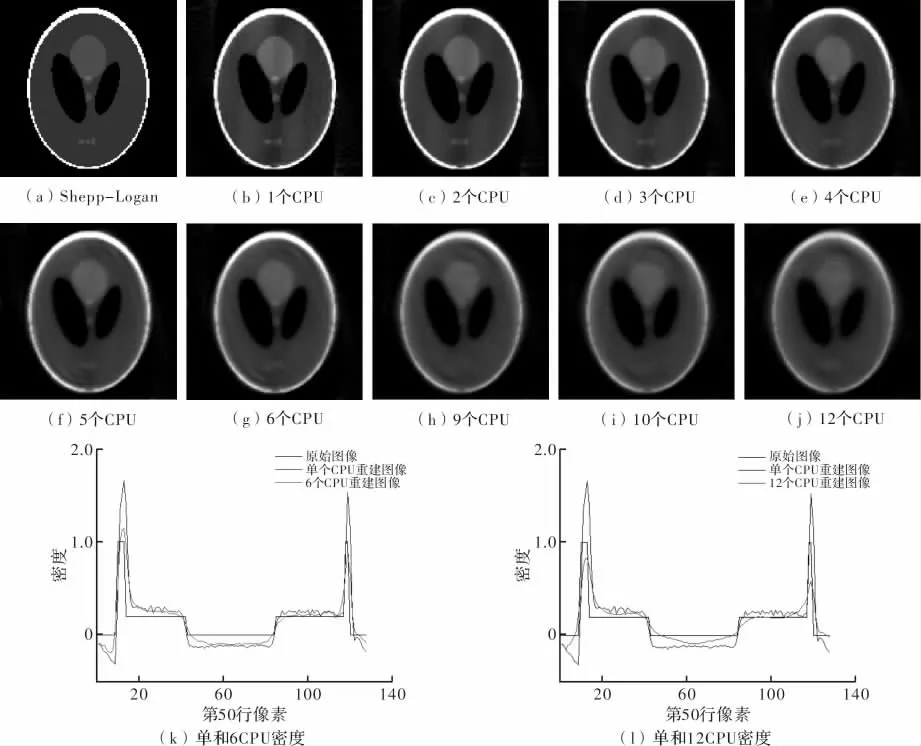
图2 不同图像在并行处理下的重建结果
在试验过程中,为了客观地评价重建质量,采用峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)、归一化均方根距离参数和归一化平均绝对距离参数来定量评价重建图像与原始图像的误差[11]。具体定义为

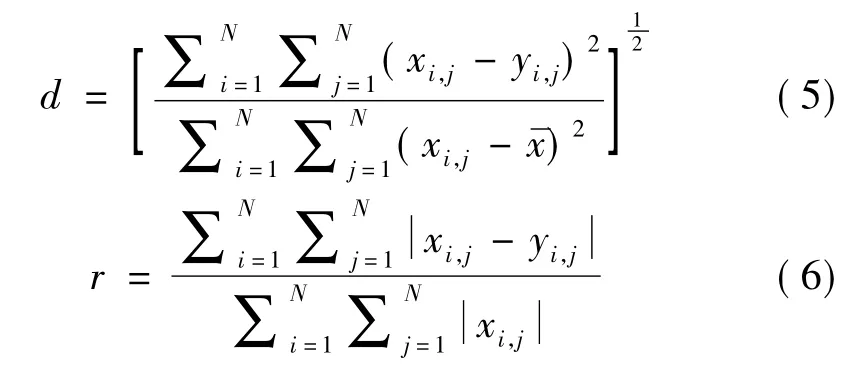
其中,MSE为均方差;xi,j,yi,j分别表示原始图像和重建图像第i行,第j列的像素密度,为原始图像密度的平均值。PSNR值越大,表示失真越少;d反映了少数点上出现的大偏差,r则反映了诸多小误差,d和r值越大,表示重建误差越大。图3和图4分别给出了Shepp-Logan头模型在112个CPU下迭代一次后的PSNR值及重建误差。

图3 不同CPU个数下的PSNR值

图4 不同CPU个数下的重建误差
如图2所示,多个CPU并行重建并加权平均的重建图像光滑清晰,CPU个数为6时图像效果最佳;图2(k)、图2(l)为原始图像与单个CPU、6个CPU以及12个CPU重建图像中间一列对应的密度值比较,可直观地看出,6个CPU下的重建图像质量优于单个CPU及12个CPU。从图3和图4可知,当CPU个数较少时,重建误差较大,重建图像的PSNR值较低;随着CPU个数的增加,重建质量越来越好,当CPU个数为6时,重建误差达到最小,PSNR值最高;此后,随着CPU个数的增加,重建误差也逐渐增大。由此可见,不能一味地增加CPU个数缩短重建时间,而降低了重建图像质量。
4 结束语
代数重建(ART)算法采用多CPU并行运算并加权平均的方式,相对于传统的串行ART算法,不仅大幅缩短了重建时间,且提高了图像的重建精度。从重建时间来看,其加速比近似等于参与运算的CPU个数;从重建精度上看,随着CPU个数适当地增加,重建质量得到改善。在工业CT应用中,由计算机集群多CPU阵列高速实现的并行运算方式具有较高的实用价值,尤其对迭代算法在线重建具有重要作用。
进一步的工作包括对迭代过程改进以提高图像精度,以及将本算法应用在三维CT重建领域。
[1]Jiang Hsieh.计算机断层成像技术:原理、设计、伪像和进展[J].谢强,译.北京:科学出版社,2006.
[2] 曾更生.医学图像重建[M].北京:高等教育出版社,2010.
[3]Siddon R L.Fast calculation of the exact radiological path for a three-dimensional CT array[J].Medical Physics,1985,12(2):252-255.
[4]Candès E J,Romberg J,Tao T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.
[5]Herman G T,Davidi R.Image reconstruction from a small number of projections[J].Inverse Problems,2008,24(4):045011-045016.
[6] 秦中元,牟轩沁,王平,等.一种内存优化的代数重建算法及其快速实现[J].电子学报,2003,31(9):1327-1329.
[7] 孙杰,渠刚荣.图像重建块迭代算法中松弛参数选取的研究[J].CT理论与应用研究,2007(2):14-19.
[8]Herman G T.Image reconstruction from projections:the fundamentals of computerized tomography[M].San Francisco:Academic Press,1980.
[9]Gordon R,Bender R,Herman G T.Algebraic reconstruction techniques(ART)for three-dimensional electron microscopy and X-ray photography[J].Journal of Theoretical Biology,1970,29(3):471-481.
[10]张志友.计算机集群技术概述[J].实验室研究与探索,2006,25(5):607-609.
[11]庄天戈.CT原理与算法[M].上海:上海交通大学出版社,1992.
