小量程窄带宽石英微加速度计敏感元件设计*

高 阳，陈 艳，李庆丰，杨贵玉

（北京遥测技术研究所 北京 100076）

前 言

加速度计自面世以来一直是军事领域最重要的惯性仪表之一，被视为惯性导航和惯性制导系统的心脏。高速飞行器在再入大气过程中，空气极度稀薄，环境压力低，消耗的能量少。由于该过程中环境恶劣，高空风速较大，受到的强风干扰严重，飞行器加速度信号具有低频小量程的特点，对其进行高精度测量在高速飞行器的气动力学参数辨识过程中具有重要意义[1]。目前可获取的硅微加速度计产品在设计中大多追求高带宽性能，尚无法同时满足高振动环境应用场合的带宽、全温精度及振动整流误差的指标要求。

针对高速飞行器再入大气应用背景下被测信号通常频率很低，且伴随着外部环境剧烈变动造成的高振动背景信号特点，本文设计了一种新型小量程窄带宽微加速度计敏感元件。该元件采用梳齿电容式结构，具有功耗低、灵敏度高、稳定性好的特点[2]。敏感元件采用石英微工艺制作，与硅材料相比，石英材料具有工艺简单、温度特性好、机械性能高的优点[3]，在振动环境下小量程加速度信号测量中具有优势。窄测量带宽既保证了可以有效测量信号，又能对环境振动背景起到抑制作用。

1 敏感元件的数学模型及检测原理

敏感元件的机械结构可以等效为一个二阶振动系统，敏感质量块通过弹性支撑梁和阻尼器与外部固定部分相连，在工作时受弹性力、阻尼力及惯性力共同作用。通过对质量块列写力平衡微分方程，当工作频率很低即近似稳态时，可得质量块位移x与输入加速度a之间的近似线性关系，如式（1）所示。

其中，M为质量块质量，k为弹性梁弹性系数，ωn为固有频率。比值M/k决定了加速度计的检测灵敏度，通常称为标度因子，它与固有频率的平方成反比。降低系统的固有频率，能提高加速度计的检测灵敏度，同时降低系统带宽。

敏感元件的电学部分主要由差分电容组成，按照外界惯性力引起电容变化形式分类，可分为变间距式和变正对面积式。本文设计的敏感元件为变间距式，其结构示意图及等效电学模型如图1所示。中心敏感质量块上的活动电极与两侧的固定电极分别构成差分梳齿电容C1、C2与C3、C4。

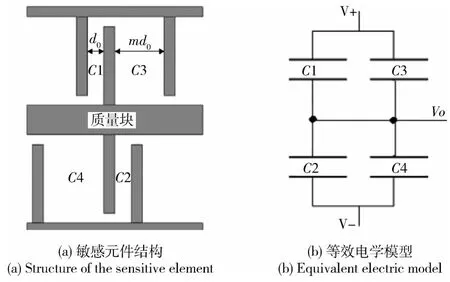
图1 敏感元件结构示意图及等效电学模型Fig.1 Structure diagram of the sensitive element and its equivalent electric model

当输入加速度为零时，动极板处于平衡位置，两差分电容间距分别为d0及md0，其中m为梳齿间隙宽窄比例因子。当有外界输入加速度a时，质量块位移x会引起差分电容的变化。本文应用z切石英晶片加工敏感元件，其材料的结构特性决定了腐蚀得到梳齿的横截面不为矩形，如图2所示。若晶片厚度为T，腐蚀侧棱到边缘的垂直距离为h，到对侧梳齿边缘的垂直距离为g0，两相邻梳齿随晶片厚度方向坐标z变化的垂直间隙为g（z），ε为空气中介电常数，H为两梳齿间的正对面积，则其电容值应由式（2）计算得到。

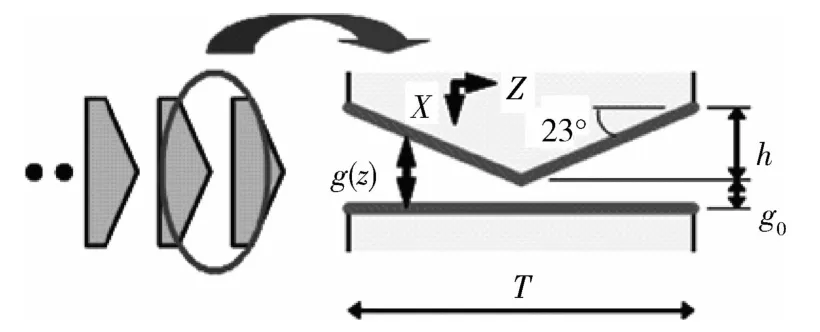
图2 石英梳齿截面图Fig.2 Section of two neighbour quartz combs

当有位移x发生时，差分电容为：

由于x≪d0，故略去高次项，保留线性主项后，可得电容改变量与位移间的关系：

将式（1）、式（2）代入式（4），可得传感器的电容灵敏度为：

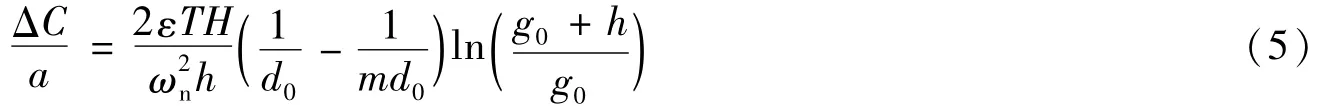
2 敏感元件的结构设计

在微电容式加速度计中，一般通过微机械结构检测电容的变化量测量加速度的大小，达到非电量电测的目的。由于微机械尺寸很小，在使用中微弱的电容量经常被干扰噪声淹没，而采用差动测量方式可以使相同环境下受到的干扰噪声抵消，极大提升信噪比[4]。梳齿电容的结构可分为定齿均置结构和定齿偏置结构，二者的区别在于动齿与两侧定齿间距离配置是否相等，前者是等距离结构，后者是不等距离结构。本文设计了一种基于石英体工艺的定齿偏置型变间距式敏感元件。

加速度计敏感元件阻尼ζ与带宽B的关系可表示为[5]：

其中fn为敏感元件的固有频率。为获取10Hz左右的窄带宽以及较高的信噪比，加速度计需要大的工作阻尼，故敏感元件采用较大的中心质量块、较长的梳齿和较小的齿间距，并设计了上下盖板结构，以在两动齿与定齿间获得比较大的压膜阻尼。另外针对元件的抗过载需求，在静齿的框架上设计了限位器，以防止传感器受过大载荷作用时梁发生过大形变而造成传感器损坏。支撑梁的刚度在敏感元件工作过程中起重要作用，MEMS器件设计中常见的弹性梁结构有固支直形梁、L形折叠梁、U形折叠梁、蛇形折叠梁等[6]。其中，U形梁结构简单，检测模态刚度小而在其他方向刚度大，交叉耦合影响小，具有应力释放作用，对于需要二阶及二阶以上模态频率远大于检测模态频率值的敏感元件来说，U形梁的综合性能较好，振幅适中，易于满足要求。在工艺参数的制约下，本文通过对加速度计结构诸参数进行仿真与综合，得到优化后的加速度计结构与设计参数，建立了敏感元件的结构模型，如图3所示。

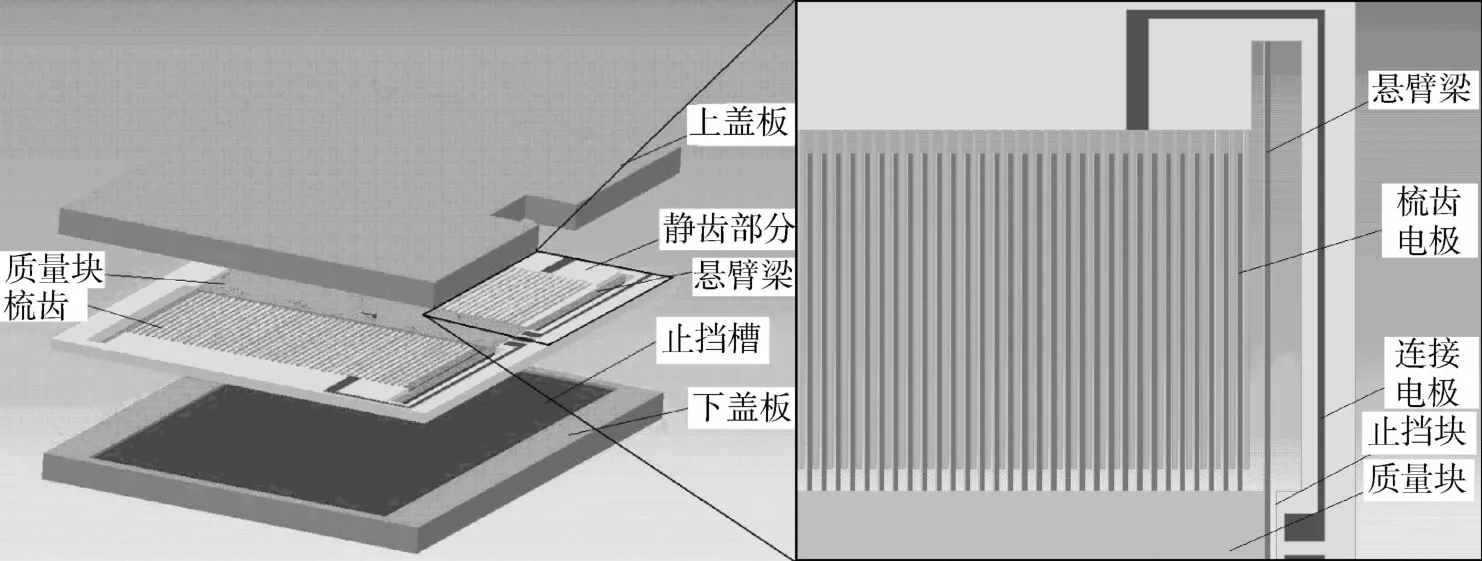
图3 敏感元件结构Fig.3 Structure of the sensitive element

3 敏感元件的仿真分析

3.1 模态分析

采用有限元方法，利用有限元仿真软件对敏感元件进行模态仿真分析。对于单轴加速度计，一阶模态为质量块沿敏感运动方向的振动模态，而第二、三等更高阶模态是其他非敏感振动模态。为了保证加速度计的精度，一般要根据模态分析的结果采用合理的尺寸搭配，使敏感模态固有频率与非敏感模态固有频率尽量大地分离，以减小交叉轴干扰。本模型采用石英材料，固定梳齿与可动梳齿交替非对称分布在质量块两侧，两端采用U形悬臂梁带动敏感质量块运动。利用有限元仿真软件对模型进行模态仿真，前4阶模态的振型图如图4所示，前6阶模态固有频率数值见表1。仿真显示，第一阶模态固有频率为216.84Hz，第二阶模态与工作模态固有频率间隔大于1.7kHz，可有效避免模态干扰。

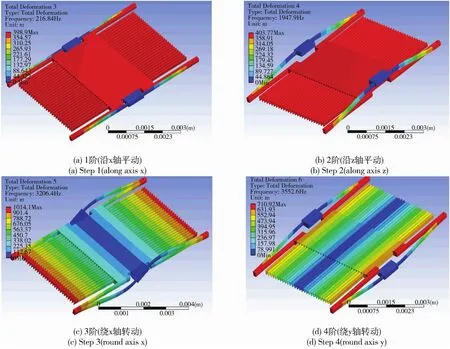
图4 敏感元件前4阶模态振型Fig.4 First 4 vibration modes of the sensitive element

表1 敏感元件前6阶模态固有频率数值Table1 Natural frequency values of first 6 modes of the sensitive element

3.2 过载分析

3.2.1 x方向

x方向为敏感元件的敏感运动方向，在未设计附加抗过载结构时，静态分析结果显示，敏感元件在x方向加载100g（g为重力加速度数值，约为9.8m/s2，下同）加速度时，最大应力值已经大于石英材料的屈服强度值（100MPa）。为提升x方向的抗过载能力，在该方向设计了冲击止挡块，其与敏感质量块的间隔约为5μm。利用有限元仿真软件在x方向加载加速度峰值6000g、时间为0.15ms的半正弦冲击载荷作为敏感元件抗过载能力的分析标准，如图5所示。为简化起见，将敏感元件两侧的梳齿结构用同等质量的质量块代替，分析的应力云图结果如图6所示。仿真结果显示，弹性支撑梁与敏感元件的连接处所受应力较大，最大应力点位于止挡块上，其值为83.225MPa，小于石英材料的屈服强度。图7所示为仿真得到的最大应力点处应力值随时间的变化曲线，图8所示为选取质量块末端一节点在载荷加载过程中的运动轨迹。仿真结果显示，止挡结构在载荷作用中起到了阻止敏感元件运动的作用，且最大应力未超过材料屈服强度，未发生接触穿透，说明增加止挡结构后敏感元件可承受峰值6000g、时间0.15ms的半正弦载荷冲击，有效提升了敏感元件x方向的抗过载能力。

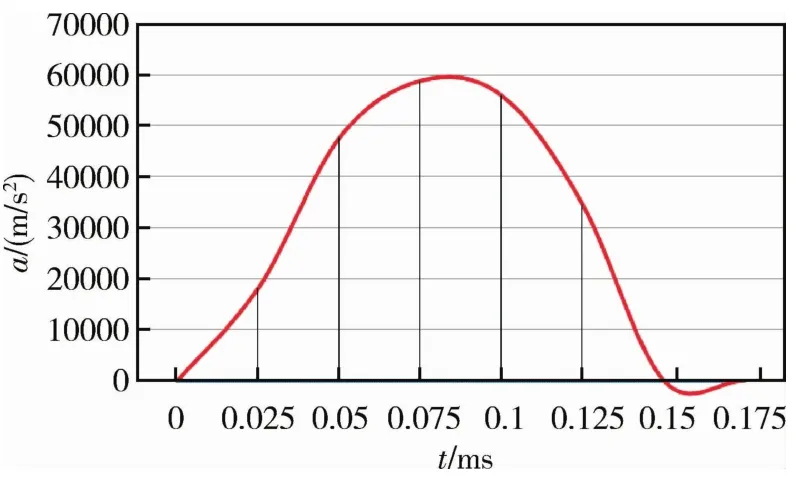
图5 加载的冲击载荷Fig.5 Impact load

图6 x方向应力云图Fig.6 Stress nephogram of axis x

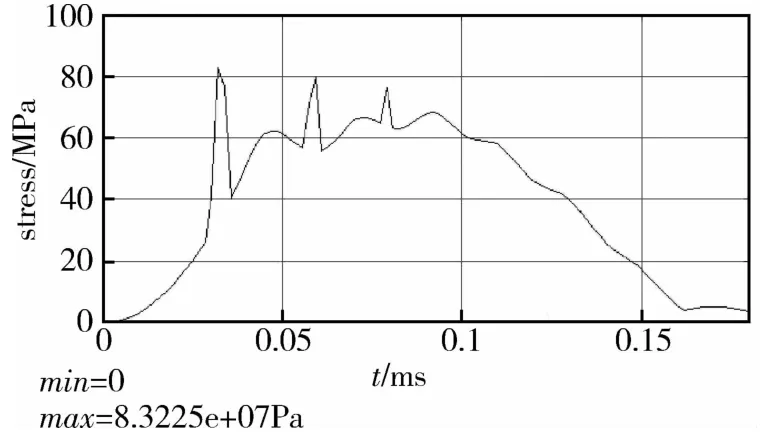
图7 x方向最大应力点处应力与时间关系Fig.7 The relationship between stress and time at the point with maximum stress on axis x

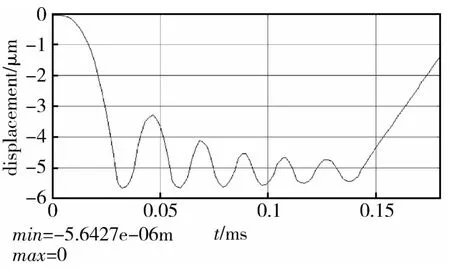
图8 敏感元件x方向位移与时间关系Fig.8 The relationship between displacement and time on axis x of the sensitive element

3.2.2 y方向

y方向为敏感元件上下表面规定的平面中与敏感元件敏感运动方向相垂直的方向。在y方向未设计附加抗过载结构，其加载图5所示加速度峰值6000g冲击载荷的应力云图如图9所示。仿真结果显示，敏感元件的最大应力值为24.3MPa，远小于材料的屈服强度值，故敏感元件在y向可承受峰值6000g、时间0.15ms的半正弦载荷冲击，无需设计附加抗过载结构。

3.2.3 z方向

z方向为与敏感元件上下表面规定的平面相垂直的方向。在未加入盖板结构时，静态分析结果显示，敏感元件在z方向加载100g加速度时，z向最大位移为9.92μm，最大应力为38MPa。根据应力与位移随加载量的线性关系可知，敏感元件可承受的最大加载量仅约为260g。而在加入与敏感元件间距约8μm的盖板结构后，其加载图5所示加速度峰值6000g冲击载荷的应力云图如图10所示。仿真结果显示，最大应力点处应力值为81.47MPa，小于石英材料的屈服强度。图11所示为仿真得到的最大应力点处应力值随时间的变化曲线，图12所示为选取质量块末端一节点在载荷加载过程中的运动轨迹。仿真结果显示，载荷加载过程中敏感元件位移被限制，最大应力未超过材料屈服强度，未发生接触穿透。故盖板结构除增大空气阻尼外，同时也可在载荷作用中起到附加抗过载结构的作用，有盖板结构时敏感元件可承受峰值6000g、时间0.15ms的半正弦载荷冲击，有效提升了敏感元件z方向的抗过载能力。

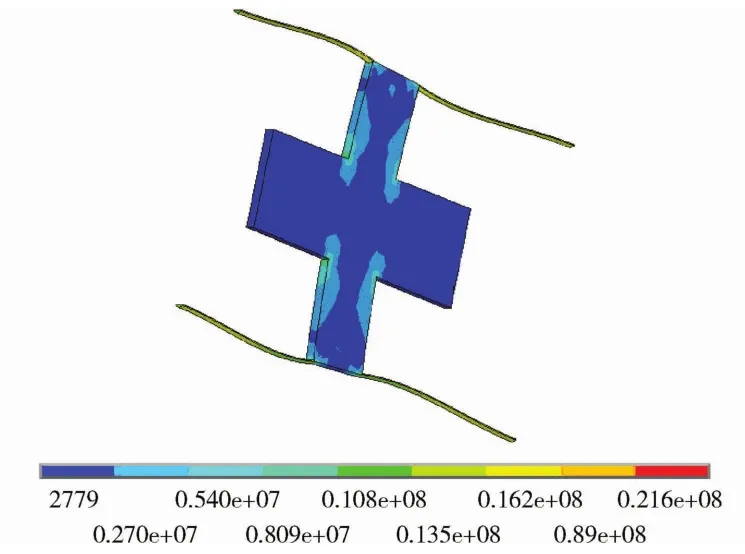
图9 y方向应力云图Fig.9 Stress nephogram of axis y

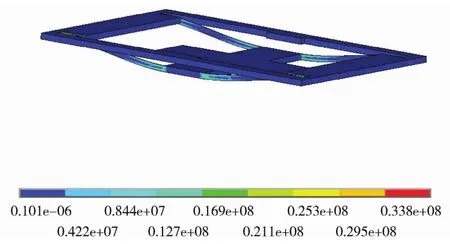
图10 z方向应力云图Fig.10 Stress nephogram of axis z

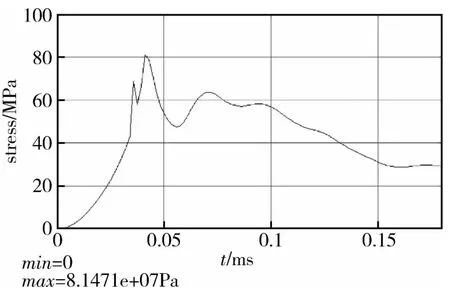
图11 z方向最大应力点处应力与时间关系Fig.11 The relationship between stress and time at the point with maximum stress on axis z

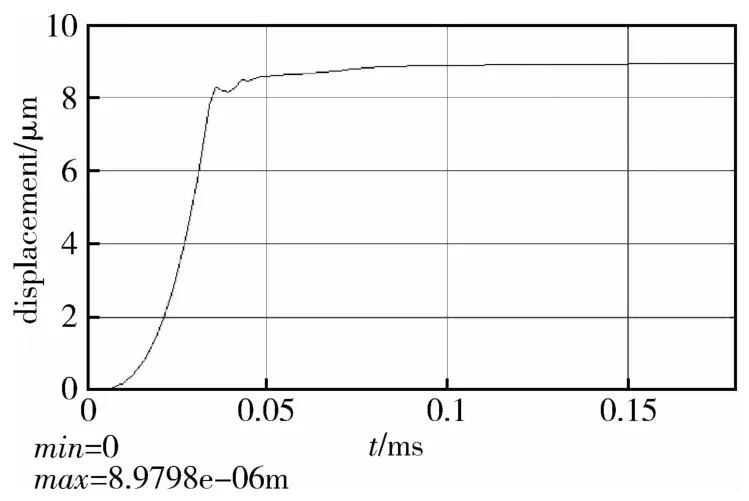
图12 敏感元件z方向位移与时间关系Fig.12 The relationship between displacement and time on axis z of the sensitive element

3.3 随机振动分析

利用有限元仿真软件对敏感元件施加功率谱PSD（Power Spectral Density），进行随机振动分析。功率谱曲线如图13所示，按照随机振动条件20Hz～80Hz：+3dB/oct、80Hz～350Hz：0.04g2/Hz、350Hz～2000Hz：-3dB/oct，以及加速度总均方根值arms=6.06g条件输出，对应每个点的谱密度值为：20Hz处（点1）0.01g2/Hz；80Hz处（点2）0.04g2/Hz；400Hz处（点3）0.04g2/Hz；2kHz处（点4）0.007g2/Hz。

3.3.1 x方向随机振动分析

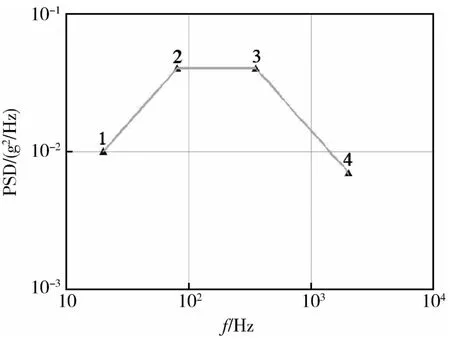
图13 施加的振动功率谱图Fig.13 PSD added on the sensitive element

在x方向即敏感元件的敏感运动方向施加上述功率谱，其1σ应力响应与1σ位移响应如图14所示。仿真结果显示，敏感元件只在x方向产生位移，最大应力点出现在弹性支撑梁上，其值约为32.72MPa，小于石英材料的屈服强度。加入不同阻尼比值，得到1σ应力响应与1σ位移响应情况如表2所示。仿真结果显示，当阻尼比增大时，x方向位移减小，应力值也相应减小，故阻尼环境有利于减小敏感元件在x方向运动时受随机振动的影响。

表2 x方向不同阻尼比时的随机振动结果Table2 Random vibration response results with different damp ratios on axis x

3.3.2 y方向随机振动分析

在y方向施加上述功率谱，并加入不同阻尼比值，分析结果见表3。仿真结果显示，敏感元件除在y方向产生位移外，在x方向也会产生位移，当阻尼比为0.6时，在两个方向上得到的1σ应力响应与1σ位移响应情况与无阻尼时相比均会减小一个量级，故阻尼环境有利于减小敏感元件在y方向运动时受随机振动的影响。

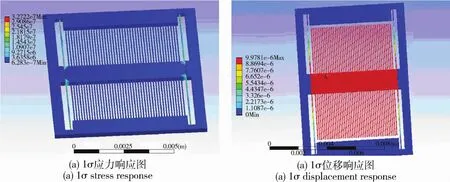
图14 x方向随机振动响应图Fig.14 Random vibration response on axis x

表3 y方向不同阻尼比时的随机振动结果Table3 Random vibration response results with different damp ratios on axis y

4 工艺制作与频响测试

采用石英湿法腐蚀体工艺对敏感元件进行了制作，整个梳齿结构即静齿与动齿同步制备。梳齿侧壁通过蒸镀金属电极膜层形成平板电极，上下盖板结构采用石英材料金-金键合工艺制作。腐蚀出的梳齿结构及最终制备的敏感元件如图15和图16所示，工艺流程如图17所示。

图15 腐蚀的梳齿结构Fig.15 Comb finger structure eroded

图16 制作的敏感元件Fig.16 Sensitive element made

图17 敏感元件工艺流程Fig.17 Technique process of the sensitive element

采用简单环形二极管电容检测电路[7]，对制作的敏感元件进行了频响测试。将元件封装并与电路连接后，利用水平振动台进行（1Hz，200Hz）区间的频响实验，拟合曲线结果如图18所示，拟合数值见表4。从扫频结果可见，工作带宽（-5%带宽）约8.9Hz，处于过阻尼状态，符合窄带宽的应用要求，且固有频率测试值215.4Hz与有限元分析结果216.84Hz接近。

图18 敏感元件幅频响应曲线Fig.18 Amplitude-frequency response curve of the sensitive element

5 结束语

本文从飞行器的气动参数辨识中对振动环境下低频小量程加速度信号的高精度测量需求出发，设计了一种新型石英梳齿电容式微加速度计敏感元件。利用有限元分析软件对设计的元件进行了仿真分析，采用α型石英材料湿法腐蚀体工艺制作了敏感元件，并对其进行了频率响应测试。分析结果表明，该石英敏感元件具有窄带宽、小量程、大阻尼的特点，适用于强振动环境下低频小量程加速度信号的高精度测量场合。通过后续不同的测量电路设计，其测量功能可得到扩展，如测量倾角等，从而形成满足振动环境下信号测量需求的系列产品。

表4 敏感元件频响参数拟合数值Table4 Fitting values of frequency response parameters of the sensitive element

[1] 贺乃宝，高 倩，姜长生.近空间飞行器变论域姿态控制研究[J].控制工程，2013，20（1）：121～123.He Naibao，Gao Qian，Jiang Changsheng.Variable Universe Fuzzy Control on Nearspace Vehicle[J].Control Engineering of China，2013，20（1）：121 ～123.

[2] Li G，Li Z，Wang C，et al.Design and Fabrication of a Highly Symmetrical Capacitive Triaxial Accelerometer[J].Journal of Micromechanics and Microengineering，2001，2（1）：48 ～54.

[3] 林日乐，谢佳维，周 倩，等.石英MEMS陀螺的结构特性分析[J].压电与声光，2011，33（4）：544～546.Lin Rile，Xie Jiawei，Zhou Qian，et al.Analysis of the Structure Characteristics of Quartz MEMS Gyroscope[J].Piezoelectrics & Acoustooptics，2011，33（4）：544 ～546.

[4] Clark W A.Micromachined Vibratory Rate Gyroscopes[D].USA： University of California，Berkeley，Doctoral Thesis，1997.

[5] Bao M.Analysis and Design Principles of MEMS Devices[M].Amsterdam：Elsevier B V，2005：115～173.

[6] 陈晓亮.差分电容式微加速度传感器稳定性研究[D].哈尔滨：哈尔滨工业大学，2009.Chen Xiaoliang.Research on Stability of Difference Capacitive Micro-accelerometer[D].Harbin：Harbin Institute of Technology，Master’s Thesis，2009.

[7] 葛海军，庄永河.一种微机械加速度计检测电路的研制[J].混合微电子技术，2012，23（2）：10～12.Ge Haijun，Zhuang Yonghe.Development of Detection Circuit for MEMS Accelerometer[J].Hybrid Microelectronics Technology，2012，23（2）：10 ～12.