砌体构件受压承载力可靠性分析

蔡云梅 赵 成 宋 勇 唐 鹏

(1 塔里木大学水利与建筑工程学院, 新疆 阿拉尔 843300)(2 中国人民解放军69218部队， 新疆 喀什 844700)



砌体构件受压承载力可靠性分析

蔡云梅1赵 成2宋 勇1唐 鹏1

(1 塔里木大学水利与建筑工程学院, 新疆 阿拉尔 843300)(2 中国人民解放军69218部队， 新疆 喀什 844700)

通过试验研究与理论分析，建立砌体构件有限元模型，并与试验结果比较，论证ANSYS中建立模型的合理性，在此基础上，运用实例采用蒙特卡洛法计算构件失效概率，及相关影响因素的敏感程度。结果表明了运用ANSYS概率分析功能实现结构可靠性分析的可行性。

砌体结构；可靠性；有限元；敏感度

目前在我国建筑结构中砌体结构仍占有很大的比重，其中大部分建筑都已进入到了检测期，需要对结构采用一定的方法进行检测评定其可靠度，根据可靠指标评定是否满足安全等级要求。可靠度的计算需要大量的样本、计算量大，因而人工计算方法的推广受到一定的限制，如果采用数值模拟方法能够满足样本数量的要求，提高计算效率，同时具有很好的准确性。

1 试验概况

根据《砌体基本力学性能试验方法标准》(GBJ 129-90)和《砌墙砖试验方法》[1]的要求，对外形尺寸为240 mm×115 mm×53 mm的普通砖，高厚比，当墙厚为240 mm时，试件尺寸为240 mm×370 mm×720 mm。为使所加荷载分布均匀需制作厚度为10 mm的钢垫板若干块，钢垫板尺寸在满足加载仪器的情况下大于240 mm×370 mm，在钢垫板四角焊接四个吊钩，方便试件的移动与起吊。同时试件顶部和底部应采用水泥砂浆找平，做浆后养护三天以上进行承载力试验，试验装置见图1所示，图2为砖砌体受压开裂，裂缝主要发生在竖向灰缝及砖块所在的位置。

按相关文献[1]规定测定砖块及砂浆的的材料参数，试验结果见表1，将此数据用于ANSYS程序中的建模分析。

图1 砖砌体抗压试验 图2 砖砌体开裂裂缝分布

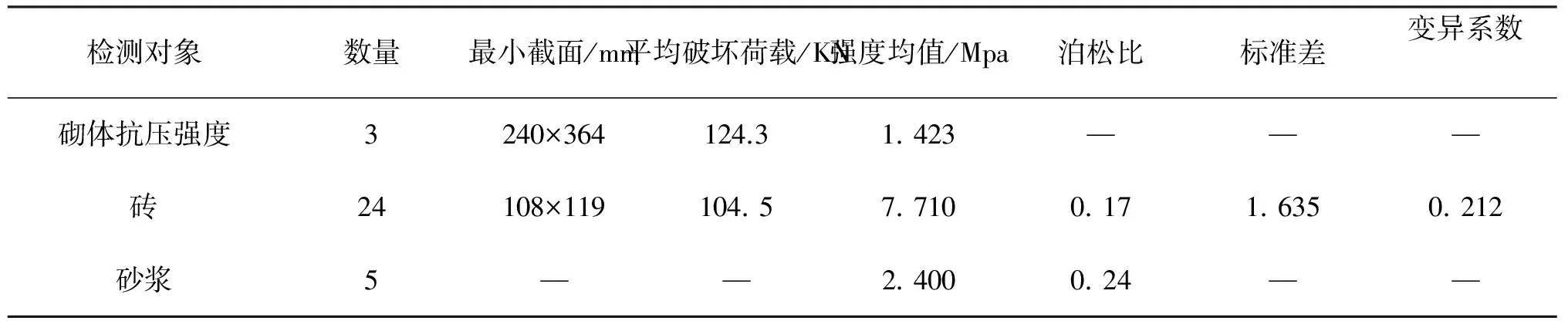
表1 相关材料参数

2 有限元建模

有限元分析的软件有很多种，Ansys软件是其中之一，由于其强大的功能被广泛应用于各专业中，在结构分析中的应用主要是数值模拟方面，通过数值模拟能够代替一些试验过程，为科学研究工作带来便利。程序中进行分析需要经过前处理、分析计算及后处理三个模块[2]。前处理模块中主要是一些参数的定义、模型的建立与网格划分；分析计算模块中需要定义分析类型、定义荷载及载荷步然后进行求解；后处理模块包括通用后处理和时间历程后处理，经过后处理用户可以获得求解过程的计算结果并对其进行显示输出。

关于Ansys中一些砌体结构的求解尚未有一般性的结论[3]。前处理砌体结构的建模主要有两种方式[4]：整体式和分离式。所谓整体式就是将块体和砂浆作为整体来考虑，这种模型适用于尺寸较大，且不需要考虑块体与砂浆之间的粘结摩擦的影响；分离式适合于较小尺寸的单个试件，是通过建立弹簧单元或接触单元考虑砂浆与块体间的相互作用，这两种方法可以根据实际要求加以选择也可相互结合使用。本文选择分离式建模，考虑块体和砂浆特性选择Solid65单元，主要原因在于该单元能够模拟类似混凝土的开裂及压碎。

表2 模型材料参数

表3 荷载分布

块体与砂浆的本构关系参照相关文献砖材料本构关系近似选用下式[5]：

其中fc取为块体的单轴抗压强度ε0=0.0015

砂浆的本构关系近似用下式表示[6]:

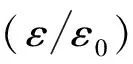
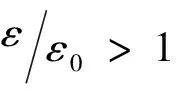
其中为砂浆的抗压强度，ε0=0.002εcu=0.0033

对于块体与砂浆间的相互作用采用接触单元加以连接，本文采用面—面接触单元，TARGE170模拟目标单元，CONTA174模拟接触单元，块体和砂浆破坏准则均选用Willia—Warnker五参数破坏准则[7](表2)，建立的有限元模型如图3，边界条件为底面完全固定的形式，顶面作用均布荷载按分步加载，见表3。

经过求解分析结果如下：X向应变分布如图4，裂缝分布情况如图5，由应变等值线图可以看出较大的应变集中在竖向灰缝对应的位置处，竖向的灰缝首先发生破坏，使得灰缝处的块体处于复杂应力状态，裂缝进一步发展导致砖块开裂，图5为构件裂缝分布图，荷载施加至30%左右破坏荷载时出现一些细小裂缝，试验过程中开裂荷载为破坏荷载的40%左右，通过模拟分析结果与试验对比可以得出模型的破坏与试验结果基本一致，差别存在的原因在于程序中的模型施加面部荷载是完全接触，在试验中为了保证荷载施加均匀分别在试件的上下做浆后加了一块钢板，由于试件在砌筑或制作的过程中一些因素的影响使得其与数值模拟仍存在一定差别。

3 可靠性计算

结构的可靠性是指结构在规定的条件下和规定的时间内完成预定功能的能力。在进行结构设计时有两种常用的方法，定值设计法与概率设计法。定值设计法假定各设计变量为确定的量，依据一定的安全系数进行结构设计；概率法，早在20世纪初就有学者将概率论与数理统计应用于结构安全度的研究[8]，概率设计方法认为，作用于结构上的真实外荷载及结构的真实承载力都是概率意义上的量，设计时不可能精确的确定他们，他们服从一定的分布。通过对各随机变量统计参数的运算求得功能函数特征值，并利用与失效概率有一一对应关系的可靠指标来衡量可靠度，这就是近似概率法，也是目前计算结构可靠度的主要方法。

可靠性分析时，常以“极限状态”为标志，当结构或构件达到不满足它的某一规定使用功能的某一特定状态时，这个状态就称为极限状态，文中采用极限状态方程为：

Z=[σ]-σvon

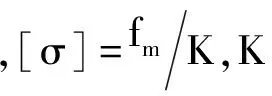
根据以上步骤在进行结构可靠性分析时首先由分析结果中提取相关参量，如：强度、应变等作为控制结构的失效参量；其次，选择影响结果参量的各不确定因素作为随机输入变量，如材料特性、构件尺寸、荷载大小等，通常假定这一类变量服从某种分布，如：正态分布、对数正态分布、均匀分布等，再选择近似概率分析法，比如蒙特卡洛法、响应面法等。通过分析得到各控制参量的概率分布函数曲线及各影响因素敏感程度。

图3 砖砌体抗压有限元模型 图4 应变分布图 图5 裂缝分布图

算例：以砌体轴压试件为例，采用第二部分建立的有限元模型，荷载、砖块及砂浆回弹模量作为随机输入变量，根据相关文献[5，6]可假定各随机输入变量服从正态分布(图6)，数值特征值见表4。

分析方法选择蒙特卡洛法，拉丁超立方抽样法抽样(图7)，经过200次循环，概率统计分析结果中可以得到指定控制参量的累积概率分布曲线及各输入变量对各控制参量的敏感程度如图8，9。通过概率累积分布曲线可以得到满足极限方程Z<0的概率(失效概率)，推定可靠指标[10]，并评定结构是否处于安全状态，本例容许应力[σ]=0.619Mpa，则Pf=1.38922×10-3<5×10-3结构较安全， 查得可靠指标β≈3.0基本满足《建筑结构可靠度设计统一标准》中关于安全等级为二级的建筑物发生延性破坏时的可靠指标β≈3.2。根据敏感性分析结果可以得到各因素对等效应力影响程度。三个因素影响差别不大，块体回弹模量影响占37. 5%，砂浆占34. 7%，荷载占27. 8%，块体回弹模量为主要因素，砂浆回弹模量次之，第三是荷载值影响。

4 结论及有待解决的问题

本文通过对砌体结构构件数值模拟分析的结果进行概率统计分析，得到了砌体构件承载力可靠度分布函数以及影响砌体结构构件强度的各因素的敏感程度，在设计过程中针对敏感因素加以控制，使其具有较小的波动性，以保证结构具有足够的可靠性，对结构可靠度影响不显著的因素则在进行可靠性分析时可把其视为定值来处理，以减少随机变量的数目，这样就能大幅度提高结构可靠性分析的效率。另外，由于数值模拟方法具备的优势使得其在可靠性分析方面的运用有待进一步加强。

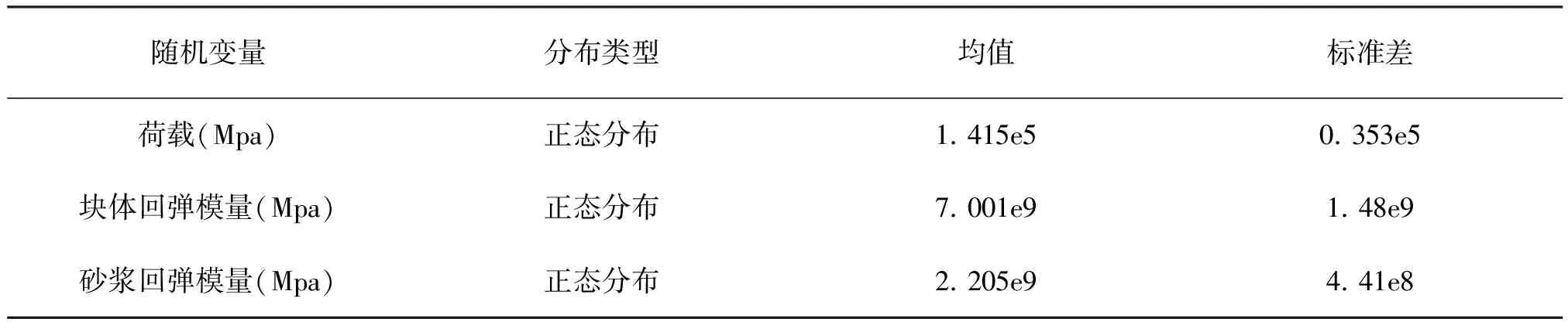
表4 随机输入变量特征值

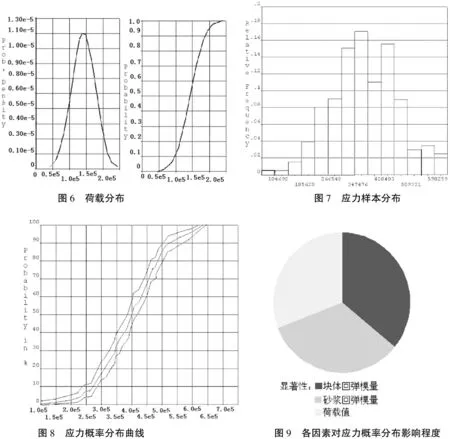
图6 荷载分布 图7 应力样本分布 图8 应力概率分布曲线 图9 各因素对应力概率分布影响程度

由于本文只考虑了少数几个因素对结构的可靠度的影响，控制指标也只选择了等效应力为参量，具有一定的局限性。实际上除了材料自身的属性参数外，结构的使用情况、测点数据的采集、分布情况也是有影响的，控制指标根据不同的强度理论应采用不同的参量，分析计算的结果都会发生变化。因而，在今后的研究中适当增加影响因素能使分析结果更加全面，为结构的鉴定加固提出更为全面的措施。

[1]GB/T2542-2003.《砌墙砖试验方法》[S].

[2] 张洪才，何波.ANSYS13.0从入门到实战[M]. 北京：机械工业出版社，2011. 494-502.

[3] 李英民，韩军，刘立平.ANSYS在砌体结构非线性有限元分析中的应用研究[J].重庆建筑大学学报，2006，28(5)：90-105.

[4] 杭翠翠.砌体结构抗压及抗震承载力仿真分析与试验对比[D].湖南：湖南大学，2011.21-25.

[5] 刘桂秋.砌体结构基本受力性能的研究[D].湖南：湖南大学，2005.13-51.

[6] 过镇海，时旭东.刚劲混凝土原理和分析[M].北京：清华大学出版社，2003:15-23.

[7] 罗如登.Ansys中砼单元Solid65的裂缝间剪力传递系数取值[J].江苏大学学报(自然科学版)，2008,29(3)：169-172.

[8] 赵国藩，曹居易，张宽权.工程结构可靠度[M]. 北京：科学出版社，2011: 3-22.

[9] 张伟.结构可靠性理论与应用[M].北京：科学出版社，2008:44-48.

[10] 胡乃君.砌体结构[M].北京：高等教育出版社，2008:15-18.

[11]MingLiu;BaoFengSong;DanielDias;JingPan.TheResearchandApplicationofMasonryStructureReliabilityRatingMethodBasedonExtenics[J].AppliedMechanicsandMaterialsvols,2013(291-294)：1029-1038.

Analyses on the Reliability on Bearing Capacity of Masonry structure

Cai Yunmei1Zhao Cheng2Song Yong1Tang Peng1

(1 College of Water Resources and Architectural Engineering， Tarim University, Alar, Xinjiang 843300)

(2 PLA Unit 69218, Kashi, Xinjiang 844700)

Based on the experimental research and theoretical analysis, masonry structure was simulated by using ANSYS. Compared with the experimental results, the simulation results showed the model is rational. Building on this foundation, selecting example and using the monte carlo method to calculate failure probability and the sensitivity of factors. It showed that the technique of ANSYS probabilistic design analyze structure reliability is feasible.

masonry structure; reliability; finite element; sensitivity

2014-06-05

塔里木大学校长基金(TDZKSS201316)

蔡云梅(1984-)，女，讲师，硕士，主要从事结构工程研究。E-mail:314899565@qq.com

1009-0568(2015)01-0111-06

TU

ADOI：10.3969/j.issn.1009-0568.2015.01.020