基于SolidWorks和COSMOSWorks的磁轴承转子结构模态分析
2015-04-25宋骏琛
宋骏琛
SONG Jun-chen
(南京工业大学,南京 211816)
0 引言
随着磁轴承技术的不断发展,并以其无磨损、转速高、能效快等特点,已广泛应用于能源、航空等领域。磁悬浮轴承转子动态性能的好坏更直接关系到系统运作的稳定性和安全性,所以对其进行动力学分析是转子系统的设计、特性的研究以及故障时的分析等的关键。在磁轴承转子运转的过程中随着转速的增加,转子振幅不断变大,当达到临界转速时达到最大值。此时会引起剧烈的共振,从而对操作人员的人身安全和操作过程的稳定性产生严重的威胁。在磁轴承转子运转的过程中,随着转速的增加,转子振幅不断变大,当达到临界转速时达到最大值。此时会引起剧烈的共振,从而对操作人员的人身安全和操作过程的稳定性产生严重的威胁。因此有效控制其工作转速通过临界转速的动力学研究刻不容缓。通常分析磁悬浮轴承转子的动态特性包括传递矩阵法和有限元法[1],传统的传递矩阵法编程繁琐、复杂、精度低,且对形状复杂的模型不具备很有效的运算和分析,尤其是遇到求解高速大型转子的动力学问题时数值很有可能不稳定[2]。而有限元法容易上手,整个操作过程通俗易懂,一目了然,且适用性强,可以有效的在分析环境不同的状态下对分析体的不同零部件做出很形象的振动分析,从中得到有效的结论来处理科研人员实际操控中的缺陷。文献[3]以磁轴承转子系统组成及工作原理为基础,用ANSYS建立模型,采用Subspace法得到了前四阶固有频率和振型,并用锤击法验证了上诉分析的可行性和有效性;文献[4]利用NASTRAN有限元软件分析了磁轴承转子系统的动态特性,研究了阻尼参数变化对性能的影响,识别了磁轴承的动态特性参数;文献[5]使用SolidWorks在有无偏心载荷与偏心质量的情况下分别进行了薄膜蒸发器转子的模态及稳态不平衡分析,结果表明偏心对固有频率影响较小,很有效的为其安全性能提供了监测的依据;文献[6]采用SISO的模态参数识别法,用NASTRAN软件建立了磁悬浮轴承-转子系统的三维有限模型成功获得了前4阶固有频率与振型,在考虑了悬浮条件下磁轴承刚度及阻尼对系统的影响下,同样用锤击法对系统进行了试验模态分析;文献[7]基于系统传递函数的刚度与阻尼特性的理论建立了用来研究磁轴承转子系统动力学特性的方法,对一个实用型的制氧机的研制进行了验证。综上所述,有限元软件在动力学分析中应用广泛,可以很有效的研究磁轴承转子系统的动态特性;而ANSYS经典等软件需要很复杂的命令流以及一定的编程基础,操作较难。SolidWorks软件建模快捷、方便,结合COSMOSWorks环境分析下的有限元法,可以划分很精密的网格得到很高的精度;自带的FFE技术分析时占用内存少,时间短,效率高,很巧妙地兼顾到了模型的完整性。故本文以SolidWorks建模结合内置的COSMOSWorks插件为例对磁轴承转子部件做了结构模态分析。分别考虑了自由状态和受迫状态下的模态分析:利用磁悬浮轴承支撑刚度可调节的特点分别对柔性和刚性下的两种约束做出了分析和对比;考虑了离心力、电机扭矩等引起的受迫振动对固有频率的影响,以达到最优动态特性下的稳定悬浮。
1 建立转子模态方程
转子模态分析是动力学分析的基础,也是瞬态响应分析,谐响应分析的开始。所以模态分析质量的好坏直接决定整个动力学分析的精度,更是为接下来的动力学分析创造一个良好的开端[7]。这里将转子系统离散成为有限个数的单元体,根据弹性力学理论,动力学微分方程为:

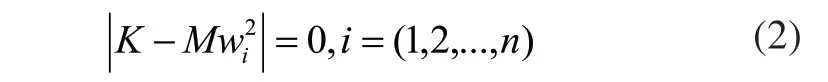
2 三维模型的建立
使用SolidWorks根据磁轴承转子二维工程图的尺寸分别建立磁悬浮轴承转子、电机转子、飞轮等零件。考虑到转子部件间的材料不同,故不可将整个磁轴承转子视为一体。这里分别完成零件三视图以后进行无缝无摩擦装配,彼此间的装配关系为过盈配合。忽略分析环境的影响或者内能产生的热磨损影响,加工精度装备质量的载荷等外界因素的干扰。因为模态分析的时候倒角、圆角等微小的细节在接下来零部件接触的时候不能很顺利的符合分析的条件,且划分网格的时候难于定义,而这些细节对分析结果几乎造成不了误差,故忽略不计以减少不必要的麻烦[8]。模态分析必须的材料具备密度、杨氏模量、泊松比三个条件。具体材料分别定义转子材料系数如表1所示。

表1 转子材料系数
转子部件三维图如图1所示。
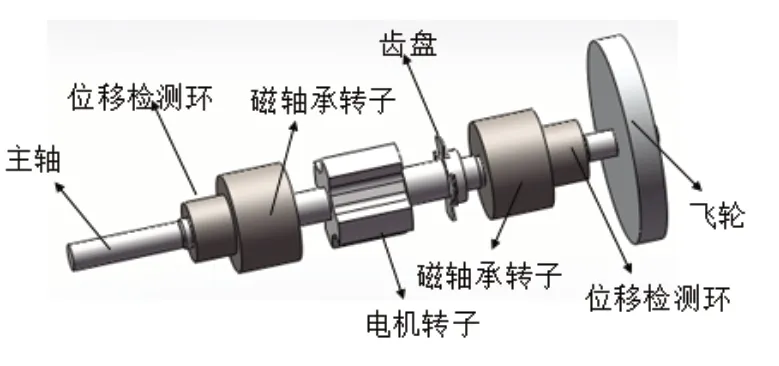
图1 转子部件三维图
3 网格划分
网格划分是对装配三维几何体进行离散化的一个过程。根据实际运转中可能造成的影响对不同的零件部位施加不同精度的网格。这些网格有长方形、三角形等,为相对小而形状简单的有限单元。为了得到较高的分析精度,这里采用二阶实体四面体单元。即每个2阶四面体单元具有10个节点(4个角点,6个中间节点)每个节点分布三个自由度。划分网格后单元总数48518。线性分析下的模态分析不考虑转子部件彼此间的摩擦与接触[9],这里选择COSMOSWorks自带的高效率的FFEPlus求解器。

图2 划分网格后的转子部件
4 自由模拟算例分析
如上所述本算例分析的目的是求解自由状态下的模态分析,而无阻尼自由振动模态分析是分析体固有的特性,故无需附加任何载荷,这里重力的因素也忽略不计。但实际操作过程中的模态分析必须加载约束条件。不同的约束条件会造成很大差异的分析结果。考虑到磁轴承支撑的支撑刚度是可以调节的,故这里以此为出发点分别考虑理想状态下的刚性和实际运转中的柔性两种不同状态下的情景。
4.1 柔性支承状态下的算例模拟
磁悬浮轴承支撑和普通机械轴承支撑相比具有刚度可调节优势,实际运转过程中一般为柔性支撑,即弹性支撑。这里磁悬浮轴承起到了刚度和阻尼的作用,即左右磁轴承支撑力不妨可以视为两个弹簧的弹性阻尼支撑。又因为本算例为自由状态,因而忽略阻尼。根据磁轴承实际工作原理,将弹簧单元定义为外端固定,内端自由约束[10]。分析过程中对磁轴承转子部件进行弹性支撑。
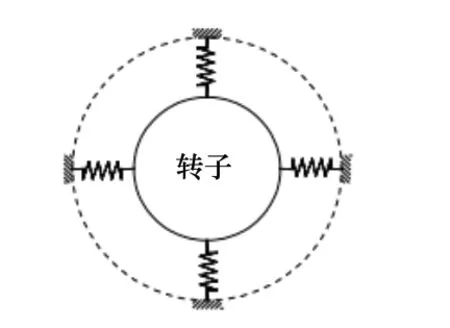
图3 弹性支撑示意图
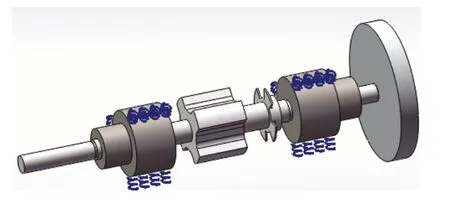
图4 弹性支撑约束
由于实际操作过程中刚度可以灵活调节,这里设轴承座弹性支撑为50N/um,作为典型的柔性状态下的支撑。得出的转子振型图和固有频率如图5所示。

图5 弹性支撑前四阶振型图

表2 基于柔性支撑的前四阶固有频率
为了更完善的分析支承刚度对转子一阶固有频率的影响,这里设以25N/um为初始状态的支承刚度,步长为25N/um依次递增,研究不同支撑刚度状态下一阶固有频率的变化。

表3 支撑刚度小幅度递增时的一阶固有频率

图6 支撑刚度小幅度递增一阶固有频率变化曲线图
图中横坐标设置的为6个支撑刚度,纵坐标为一阶固有频率。如图所示,当支撑刚度变化较小时,一届固有频率在300Hz~400Hz间逐渐递增,斜率逐渐变小。
4.2 刚性支承状态下的算例模拟
理想状态中的刚度视轴承为绝对刚性。这里为了更好地得出支撑刚度对整个固有特性的影响,故考虑刚性状态下的情况[11]。软件操作中将磁轴承转子的圆柱面进行径向位移约束,这里将模态坐标下的两个径向方向X、Y方向固定。

图7 刚性支撑约束
添加约束之后选择运行,结果如表4所示。

表4 基于刚性支撑的前四阶固有频率

图8 刚性支撑前四阶振型图
5 受迫模拟算例分析
在转子实际的旋转过程中,由于转子质量不平衡及高速旋转时不可避免的离心力,会对转子部件造成受迫振动。同样的结构在不同应力状态下或是有无外部载荷的情况下表现出不同的动力学特性。另如上所述,受到的离心力需施加,这里离心力的受力点位于转子质心的位置;由于电机的通电才造成转子部件的运作,这里电机定子对电机转子必有一扭矩的作用;转轴在稳定旋转时与磁悬浮轴承定子没有接触,彼此间电磁力中和,故没有轴承载荷的作用力。综上所述,转子旋转时的受迫振动主要由离心力、电机扭矩等产生。

图9 受迫振动下所受外力示意图

图10 受迫状态柔性支撑前四阶振型图
使用如自由振动下同样的约束条件也分别在刚性、柔性状态下的模拟算例进行分析。

表5 受迫状态下基于柔性支撑的前四阶固有频率

图11 受迫状态刚性支撑前四阶振型图

表6 受迫状态下基于刚性支撑的前四阶固有频率
5.1 离心力载荷对固有频率的影响
由于转子材料不统一,形状不对称,装配过程产生误差等因素,难免会造成转子质量不平衡的后果,从而产生偏心[12]。转子质量偏心会造成不可避免的离心力。即使有很高的加工精度,质量不平衡也难于避免。而旋转机械在实际运转状态时有保持其旋转方向(旋转轴的方向)的惯性,迫使这种惯性持续发生的作用力也是离心力。根据离心力公式:

其中,F为离心力,m为转子质量,w为自身旋转角速度。
可得知离心力和角速度、偏心距有关。且角速度越高,离心力越大。当磁悬浮轴承转子转速达到一定程度时,不平衡振动的幅值有越过保护气隙的危险,造成系统失控,甚至严重影响动态性能的安全运作。因此这里从不同角速度下产生的离心力为出发点,研究其对固有频率的影响,也是为磁轴承转子动态性能的提升做出参考。启用COSMOSWorks环境下的设计算例,这里不妨设初始旋转角速度频率为300Hz,步长为200Hz,即公差为200的等差数列单调递增。

表7 不同角速度下离心力对一阶固有频率的影响
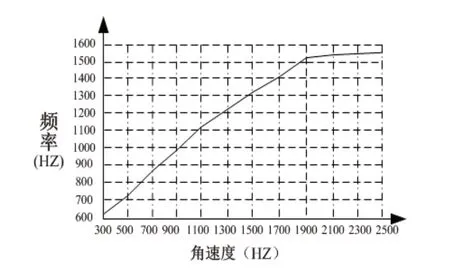
图12 不同离心力状态下一阶固有频率变化曲线图
如图12所示,横坐标为12个不同设置情形下的转子旋转角速度,纵坐标为一阶固有频率对应的值;表7算出了具体对应值的大小。由曲线图可知在离心力随着角速度递增的情况下,一阶固有频率在300Hz~1700Hz的范围内递增速度很快,1700Hz~2500Hz范围内递增速度缓慢,趋于平缓,接近临界值。
5.2 电机扭矩对固有频率的影响
磁轴承转子在启动的过程中需要依靠电机扭矩才能正常运转。随着电机负载的变化,扭矩可以在合理的范围内作出相应的调整。当扭矩达到15Nm时所对应的电机功率通常为950w左右。这里以1N.M扭矩为初始值,步长设为2N.M,分析不同扭矩状态下,磁轴承转子一阶固有频率的变化。

表8 不同扭矩状态下的一阶固有频率

图13 一阶固有频率随扭矩变化的曲线图
由表8及图13分析结果表明,随着电机扭矩的不断增大,固有频率只在393.5Hz该值的左右范围内变动,因此对磁轴承转子一阶固有频率几乎造成不了影响,只是在特别微小的范围内随着扭矩的增大,一阶固有频率单调递减,由此可以得出扭矩的变化对固有频率的影响是可以忽略不计的。
6 结论
1)磁悬浮轴承支承刚度的不同对转子系统的各阶临界转速影响较大,由本文所分析选取的两个刚度可以很明显的看出:支撑刚度是造成转子固有频率巨大变化的因素之一。因此合适的刚度是精确计算固有频率的重要因素。
2)柔性支撑状态下的约束变形幅度较小,固有频率的调整可以通过改变转子轴承支撑刚度的方法有效调整。一阶固有频率下飞轮变化程度较大,可提升其自身刚度或改变材料系数避免实际运转时超过一阶临界转速。前三阶主要Z-Y平面发生幅度变化,第四阶在Z-X平面形变。振幅主要出现在飞轮及电机转子。
3)刚性支承约束条件下前三阶变化幅度主要在飞轮和主轴末端,第四阶发生剧烈形变。说明前三阶变化幅度小,第四阶骤然大幅度提升。前三阶主要为Z-X平面的共振变化,第四阶为Z-Y,与柔性状态正好相反。
4)刚性条件下的固有频率比柔性状态下的大的多,总体数值变化上升程度更为厉害。由此可以通过加大支撑刚度的方式来提高临界转速,以此提升安全性能。
5)当考虑离心力等外力引起的拉伸应力的时候,转子固有频率有逐渐增大的趋势,且变化幅度较大。
6)随着角速度的增加,离心力逐渐变大。一阶固有频率随着转子自身角速度的增大而增大,转速小的状态下变化幅度很大,当转速大到一定值的时候趋于平缓,变化幅度小,达到临界值状态。
7)电机扭矩引起的受迫振动对转子一阶固有频率几乎产生不了影响,故在实际运转中可以忽略扭矩的作用。
8)本文对磁轴承转子的模态分析为进一步实现接下来的动力学分析奠定了基础,也为磁轴承开关磁阻电机的安全运行提供了监测依据。
[1] 钟一谔,何衍宗,等.转子动力学[M].北京∶清华大学出版社.1987.
[2] 刚宪约.多转子系统振动分析的整体传递矩阵法研究[D].大连∶大连理工大学,2002.
[3] 李克雷,谢振宇.基于ANSYS的磁悬浮转子的模态分析[J].机电工程,2008,(25)1∶1-3
[4] 张宝强.磁轴承—转子系统的有限元模型修正及相关问题研究[D].南京∶南京航空航天大学,2009.
[5] 杨玉强,贺小华.薄膜蒸发器转子动力学性能的有限元分析[J].机械设计与制造,2010,(10)∶45-47.
[6] 周瑾,蔡永飞.磁悬浮轴承转子系统的理论与试验模态分析[J].武汉理工大学学报,2010,32(6)∶889-891.
[7] 闻邦春,顾家柳,夏松波,等.高等转子动力学∶理论、技术及应用[M].北京∶机械工业出版社,1999.
[8] 汪希平,朱礼进,等.主动磁轴承转子系统动力学特性的研究[J].机械工程学报,2001,37(11)∶7-12.
[9] 王加峰,王树林,等.旋叶式压缩机转子的有限元模态分析[J].机械设计,2009,26 (2)∶68-70.
[10] 张海波,杨昌茂,等.径向永磁偏置磁悬浮轴承转子模态分析[J].机械制造,2011,49(599)∶26-28.
[11] 赵鹏,王晓光.仪表磁悬浮转子系统动态特性研究[D].武汉∶武汉理工大学,2005.
[12] 魏莉,胡业发,等.磁悬浮转子质量偏心对动态特性的影响[A].第二届中国磁悬浮轴承学术会议论文集[C]∶57-61,2007.
